基于“三线”的高考试题赏析与改编
2023-04-17成树明
成树明
(山东省滨州市第一中学)
高考评价体系是物理高考命题的根本指南,也是一线高中教师指导学生备考的纲领性文件。高考评价体系在高考命题实践中最为明显的特征是三线贯通:“核心价值金线”是一份试卷的灵魂,“能力素养银线”是一份试卷的骨骼,“情境载体串联线”是一份试卷的形体。“无价值,不入题” “无思维,不命题” “无情境,不成题”已成为高考命题的主要特征。
近几年的高考物理试题是在高考评价体系理论指导下,由命题专家集体打磨出的智慧结晶,既考查了高中物理的必备知识和关键能力,也注重了物理思想和方法的考查,是高三物理教学和备考的好素材。对高考物理试题进行变式训练,做到一题多变,多题归一,是培养学生模型建构、逻辑推理与批判性思维等高阶思维的有效途径。一线教师在对高考试题进行改编和模拟题的命制过程中,也要以高考评价体系为依据,努力落实好“三线贯通”。
1 基于生活实践情境的高考试题赏析与改编
1.1 原题呈现
【例1】(2021·广东卷·13)算盘是我国古老的计算工具,中心带孔的相同算珠可在算盘的固定导杆上滑动,使用前算珠需要归零,如图1所示,水平放置的算盘中有甲、乙两颗算珠未在归零位置,甲靠边框b,甲、乙相隔s1=3.5×10-2m,乙与边框a相隔s2=2.0×10-2m,算珠与导杆间的动摩擦因数μ=0.1。现用手指将甲以0.4 m/s的初速度拨出,甲、乙碰撞后甲的速度大小为0.1 m/s,方向不变,碰撞时间极短且不计,重力加速度g取10 m/s2。

图1
(1)通过计算,判断乙算珠能否滑动到边框a;
(2)求甲算珠从拨出到停下所需的时间。
【解析】(1)设甲、乙算珠的质量为m,滑动时由牛顿第二定律,得
μmg=ma
设甲珠与乙珠碰前速度为v1,从甲珠以v0=0.4 m/s的初速度拨出到与乙珠碰撞前,由运动学公式,得
由题意知碰撞后甲珠的速度为
v2=0.1 m/s
设碰撞后乙珠的速度为v3,甲、乙碰撞时由动量守恒定律得
mv1=mv2+mv3
碰撞后乙珠做匀减速直线运动,设乙珠速度减为零时的位移为x,由运动学公式,得
联立解得x=0.02 m
因x=s2,故乙珠恰好运动到边框a
(2)设甲珠与乙珠碰前运动时间为t1,由运动学公式,得
v1=v0-at1
设碰撞后甲珠运动时间为t2,由运动学公式,得
0=v2-at2
则甲运动的总时间为
t=t1+t2
联立解得t=0.2 s
1.2 试题赏析
题目以中华传统文化中的算盘为生活实践情境进行命制,考查多物体、多过程问题。本题在落实“三线”的基础上,重点突出了“核心价值金线”的考查。“核心价值金线”主要是围绕立德树人来考查学生的政治立场和思维观念、世界观和方法论以及道德品质。爱国主义情怀、世界观和方法论、科学精神这三个方面构建起物理学科具体的“核心价值金线”。近几年高考物理试题,常以我国的重大科技成果、航天巨大成就等为情境,展示我国科技日新月异的进步,激发学生的进取意识、实现中国梦的使命感和责任感。也常以中国古代科技和物理学史为情境,感受我国古代发达的科学技术、弘扬中华优秀传统文化,激发民族自豪感,厚植爱国主义情感。通过分析解答近几年的高考物理试题,有助于学生形成科学的世界观和正确的方法论,有助于培养学生实事求是、求真务实、开拓创新的科学精神。
1.3 试题改编
【改编1】某冰壶队为了迎接北京冬奥会,积极开展训练。某次训练中使用的红色冰壶A和蓝色冰壶B质量均为20 kg,开始两壶之间的距离为s=7.5 m,运动员以v0=2 m/s初速度将红色冰壶A掷出,与静止的蓝色冰壶B碰撞后红色冰壶A的速度大小为vA=0.2 m/s,方向不变,碰撞时间极短且不计。已知两冰壶与冰面间的动摩擦因数均为μ=0.02,重力加速度g取10 m/s2。求:
(1)红色冰壶A从开始运动到停下所需的时间;
(2)两冰壶碰撞过程中损失的机械能。
【解析】(1)两冰壶在冰面上滑动时,由牛顿第二定律,得
μmg=ma
设红色冰壶A与蓝色冰壶B碰前的速度v,由运动学公式,得
v=v0-at1
0=vA-at2
红色冰壶A运动的总时间为
t=t1+t2
联立解得t=6 s
(2)碰撞过程,由动量守恒定律和能量守恒定律,得
mv=mvA+mvB
联立解得ΔE=3.2 J
【改编2】(多选)2022年2月4日北京冬奥会开幕,冰壶是冬奥会的传统比赛项目。如图2所示,某次比赛中运动员将红色冰壶A掷出,与静止的蓝色冰壶B碰撞,碰撞后两冰壶的v-t图像如图3所示。已知重力加速度g为10 m/s2,下列说法正确的是

图2

图3
( )
A.红色冰壶A与冰面的动摩擦因数为0.2
B.蓝色冰壶B与冰面的动摩擦因数为0.02
C.开始红蓝两冰壶之间的距离为7.5 m
D.碰后红色冰壶A运动的距离为1.6 m
【答案】BC
1.4 改编小结
以北京冬奥会这一重大历史事件和冰壶体育运动为情境进行改编和命制,仍突出了“核心价值金线”的考查,通过北京冬奥会的举办,使学生进一步感受到了体育精神和奥林匹克精神,进一步增强了民族自豪感和对国家未来的信心。改编1是通过情境设置与设问角度的改变进行的创作,这是试题改编常用的两种技术。由算盘改为北京冬奥会,由两个算珠改为两个冰壶,都是一个运动的物体去碰一个静止的物体,碰后都做匀减速直线运动,两题的本质是一样的。学生通过对两题的解答,可以透过现象看本质,提升模型建构能力,有利于高阶思维的养成;改编2是由改编1将文本信息改编为图像信息,并由计算题改编成选择题进行的创作,从而将试题难度也进行了降低。文本信息与图表信息的相互转换,计算题与选择题两种题型的相互转换,都是试题改编的常用技术。
2 基于学习探索情境的高考试题赏析与改编
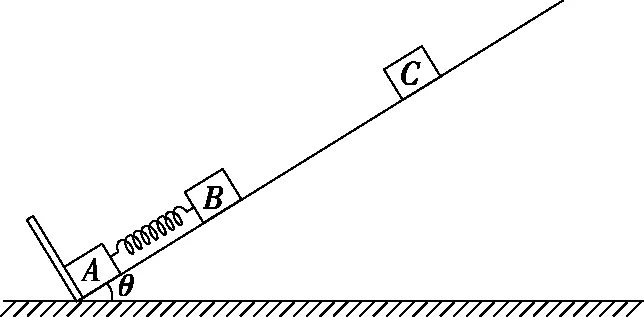
2.1 原题呈现


图4
(1)求B、C向左移动的最大距离x0和B、C分离时B的动能Ek;
(2)为保证A能离开墙壁,求恒力的最小值Fmin;
(3)若三物块都停止时B、C间的距离为xBC,从B、C分离到B停止运动的整个过程,B克服弹簧弹力做的功为W,通过推导比较W与fxBC的大小;
(4)若F=5f,请在图5所给坐标系中,画出C向右运动过程中加速度a随位移x变化的图像,并在坐标轴上标出开始运动和停止运动时的a、x值(用f、k、m表示),不要求推导过程。以撤去F时C的位置为坐标原点,水平向右为正方向。
图5
【解析】(1)从开始到B、C向左移动到最大距离的过程中,以B、C和弹簧为研究对象,由功能关系得
弹簧恢复原长时B、C分离,从弹簧最短到B、C分离,以B、C和弹簧为研究对象,由能量守恒定律得
联立方程解得
(2)当A刚要离开墙时,设弹簧的伸长量为x,以A为研究对象,由平衡条件得
kx=f
若A刚要离开墙壁时B的速度恰好等于零,这种情况下恒力为最小值Fmin,从弹簧恢复原长到A刚要离开墙的过程中,以B和弹簧为研究对象,由能量守恒定律得

(3)从B、C分离到B停止运动,设B的路程为xB,C的位移为xC,以B为研究对象,由动能定理得
-W-fxB=0-Ek
以C为研究对象,由动能定理得
-fxC=0-Ek
由B、C的运动关系得
xB>xC-xBC
联立解得W (4)小物块B、C向左运动过程中,由动能定理得 解得撤去恒力瞬间弹簧弹力为 kx1=6f 则坐标原点的加速度为 之后C开始向右运动过程(B、C系统未脱离弹簧)加速度为 可知加速度随位移x为线性关系,随着弹簧逐渐恢复原长,x减小,a减小,弹簧恢复原长时,B和C分离,之后C只受地面的滑动摩擦力,加速度为 负号表示C的加速度方向水平向左;从撤去恒力之后到弹簧恢复原长,以B、C为研究对象,由动能定理得 脱离弹簧瞬间后C速度为v,之后C受到滑动摩擦力减速至0,由能量守恒定律得 解得脱离弹簧后,C运动的距离为 则C最后停止的位移为 所以C向右运动的a-x图像如图6所示 图6 题目以常见的物块和弹簧为学习探索情境进行命制,考查了多物体、多过程问题。本题在落实“三线”的基础上,重点突出了“能力素养银线”的考查。物理观念、科学思维、科学探究、科学态度与责任为物理学科的学科素养。本题考查了物理观念中的物质观念、运动与相互作用观念、能量观念等;解答本题需要运用抽象与联想、模型与建模、推演与计算等思维方法。本题还考查了考生的理解能力、模型建构能力、逻辑推理能力、分析综合能力、信息加工能力等,这些都是物理学科的关键能力。 图7 (1)求小物块A、B碰后瞬时速度的大小; (2)求小物块B向下运动的最大位移; (3)小物块B向下运动至最低点时,求小物块C对水平面压力的大小; (4)若小物块B向上运动到最高点时,小物块C恰好离开地面,求小物块A开始下落时距小物块B的高度。 【解析】(1)小物块A下落过程,由动能定理得 小物块A、B碰撞过程,由动量守恒定律得 mv1=2mv2 解得小物块A、B碰后瞬时速度的大小为 (2)设弹簧开始时的压缩量为x0,则 mg=kx0 设小物块A、B一起运动到最低点的过程中发生的位移大小为x,由能量守恒定律得 (3)小物块B向下运动至最低点时,以小物块C为研究对象,由受力平衡得 FN=mg+k(x0+x) 由牛顿第三定律知小物块C对水平面压力的大小为 (4)小物块C为研究对象,有 mg=kx1 设此时小物块A开始下落时距小物块B的高度为H,下落过程与碰撞过程有 mv3=2mv4 小物块A、B在弹簧原长处分离,设分离时的速度大小为v5,由能量守恒定律得 小物块A、B分离后,小物块B向上运动到最高点的过程中,由能量守恒定律得 图8 (1)求小物块B碰后瞬时速度的大小; (2)求小物块B向下运动的最大位移; (3)小物块B向下运动至最低点时,求小物块A对挡板的压力大小; (4)若小物块B沿斜面向上运动到最高点时,小物块A恰好离开挡板,求小物块C开始下落时距小物块B的距离。 【解析】(1)小物块C下落过程,由动能定理得 小物块B、C碰撞过程,由动量守恒定律得 mv1=2mv2 解得小物块B碰后瞬时速度的大小为 (2)设弹簧开始时的压缩量为x0,则 mgsinθ=kx0 设小物块B、C一起运动到最低点的过程中发生的位移大小为x,由能量守恒定律得 (3)小物块B向下运动至最低点时,以小物块A为研究对象,由受力平衡得 FN=mgsinθ+k(x0+x) 联立解得 由牛顿第三定律知小物块A对挡板的压力大小为 (4)以小物块A为研究对象,有 mgsinθ=kx1 解得x1=x0=2Lsinθ 设小物块C开始运动时距小物块B的距离为L0,下落过程与碰撞过程有 mv3=2mv4 小物块B、C在弹簧原长处分离,设分离时的速度大小为v5,由能量守恒定律得 小物块B、C分离后,小物块B向上运动到最高点的过程中,由能量守恒定律得 联立解得L0=18Lsinθ 改编题情境与原题相同,改编方法是进行的空间转换,原题三个小物块及弹簧水平放置,改编1题将三个小物块及弹簧竖直放置,改编2题是将三个小物块及弹簧沿斜面放置。相同点都是两小物块与弹簧相连,另一小物块在恒力作用下运动,不同点改编题开始运动的小物块的重力不能撤去。改编题与原题的设问角度也不相同,但都突出了“能力素养银线”的考查。 高考试题是理解和把握高考评价体系的重要载体,也是进行高中物理教学的好素材。教师对高考试题的研究和解读,要依据高考评价体系,善于从三线的角度去分析和研究,从而选择恰当的高考试题用于教学的不同阶段,在高三教学和备考中更要精选高考试题。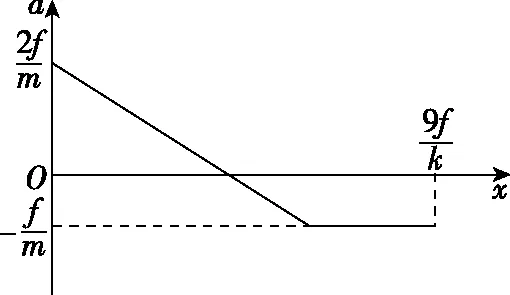
2.2 试题赏析
2.3 试题改编



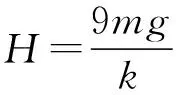


2.4 改编小结
3 教学启示
3.1 加强高考试题研究
3.2 提升教师命题能力

