无畸变共形阵列抗干扰算法的降秩处理方法

李 晗, 何 迪, 陈 新, 曲家庆

(1.北斗导航与位置服务上海市重点实验室,上海交通大学, 上海 200240;2.上海无线电设备研究所, 上海 201109)

0 引言

全球卫星导航系统(global navigation satellite system,GNSS)如今已经成为一重要空间基础设施,可为全球用户提供定位、导航和授时服务[1-2]。北斗卫星导航系统(Beidou navigation satellite system,BDS)是完全由中国自主设计和建造的多功能全球卫星导航系统。与现有的其他GNSS 类似,BDS 也被设计为能够承受一定水平的射频干扰[3],这是通过直接序列扩频技术[4]的应用来实现的,该技术能够抑制常见的噪声信号。然而,除了接收机热噪声之外,在许多情况下还存在无意和有意的干扰,破坏GNSS信号接收的可靠性。为了解决这些问题,提高GNSS 接收机的鲁棒性,在过去的几十年中涌现了许多GNSS干扰抑制方法。实践证明,空时自适应处理(spacetime adaptive processing,STAP)是最有效的方法之一。STAP技术将天线阵列与有限长度冲激响应(FIR)滤波器相结合,以加权和的形式自适应地重新排列天线的接收信号,以引导天线阵列响应波束指向所需方向。将零点指向干扰方向,使GNSS信号原样通过,同时有效抑制干扰。该方法在抑制高功率干扰方面效果很好[5]。然而,STAP 中引入FIR 滤波器会引起非线性相位响应,进而导致所需信号的失真。以往的实验表明,如果不特别注意这个问题,STAP 带来的定位误差可以达到几十米[6]。因此,在高精度GNSS应用中,必须考虑该问题,并对信号失真加以补偿[7-8]。

共形阵列是一种符合其承载表面的天线阵列,旨在实现更好的空气动力学和流体动力学性能,或出于美学考虑。因此,共形阵列在许多场景中得到广泛应用,例如用于高速飞机的雷达或BDS 接收机。传统的干扰抑制技术不能直接应用于共形阵列,因为通常假设所有共形阵列天线阵元都是全向的,并且具有相同的响应模式。然而,由于承载面的非平面曲率,共形阵列天线设计时应采用定向阵元模型,不同的天线阵元通常指向不同的方向,进而导致不同天线阵元对同一信号的响应不同。这意味着不能将单阵元响应函数作为平面阵列分析中常用的阵列流形的公因子进行分离。因此,必须修正信号接收过程的数学模型以适应上述非理想条件。目前,共形阵列信号处理的研究主要集中在模式合成和波达方向(direction of arrival,DOA)估计两个方面,对共形阵列中的干扰抑制技术关注较少[9]。

空时自适应处理技术带来的另一副作用是,当时延抽头数增大时,STAP 观测向量的协方差矩阵维数会急速增大,矩阵求逆的速度会影响到算法的实时性。而事实上在许多应用中,使用一个维数较小的子空间对观测空间进行近似时,抗干扰性能下降并不明显,但却大大减少了计算量,因而对基于STAP 的干扰抑制方法进行降秩简化有重要意义。目前常用的降秩方法包括主成分(principal components,PC)方法、互谱度量(cross spectral metric,CSM)方法和多级维纳滤波(multistage Wiener filter,MWF)方法。降秩后处理器稳态性能不可能超过全维处理器,但更小的运算量和更快的收敛速度使其瞬态性能可能略优于全维处理器[10]。降秩处理的关键在于选择合适的转换矩阵,使处理器的维数尽可能低,同时尽可能提高瞬态性能,并使稳态性能接近最佳。

通过对传统MWF 处理器结构的改进,可以进一步降低计算量,并在保证抗干扰能力的同时,不影响算法的线性相位特性,减小处理过程引起的卫星信号畸变。

1 算法原理

1.1 凸共形阵列的信号接收模型

基于共形阵列的北斗接收机不能沿用传统的阵列信号处理模型。即使采用辐射特性相同的阵元,载体表面曲率也会导致各个阵元的指向不同,进而导致在阵列天线的全局坐标系内各阵元的方向图函数不同。考虑到实际天线方向图的性能需求与模型简化,使用余弦天线模型进行讨论,其方向图函数

式中:θ,φ分别为信号在极坐标系下的入射俯仰角与方位角。

首先假设任意M元凸共形阵列的所有阵元辐射特性相同,均为余弦天线;然后根据阵列具体结构确定一个全局直角坐标系oxyz。设pm为第m个阵元在其中的空间坐标矢量,且阵元指向与当前位置载体表面的法线方向相同。定义共形因子矩阵G[9]来表征阵元方向图及阵列的共形带来的影响,G表示为

式中:g（θd,φd）表示期望信号方向的共形因子,其中θd,φd为期望信号在全局极坐标系下的入射俯仰角及方位角;g（θjk,φjk） 表示第k个干扰信号方向的共形因子,其中θjk,φjk为第k个干扰信号在全局极坐标系下的入射俯仰角及方位角,k∈{1,2,…,K},K为干扰个数;θi(θ,φ)表示第i个阵元处的本地极坐标系的入射俯仰角;T表示矩阵转置运算。结合欧拉旋转定理可以得到凸共形阵列的观测向量

式中:A为阵列流形阵列;S(n)为入射信号矢量;d(n)和jk(n)分别为期望信号和第k个干扰信号;V(n)为噪声信号矢量。定义共形阵列流形C=G☉A,则

1.2 抗干扰算法

在干扰场景复杂、干扰数多、阵元数量有限制的情况下,STAP是替代纯空域滤波处理的较好方法。此外,STAP除了调整天线阵的空域响应,还能调整时域响应,用于补偿射频、中频信号失真以及天线失配等问题。

当时延抽头数为P时,基于式(4)定义STAP信号观测向量

得到基于共形阵列的无失真空时最小方差无失真响应(distortionless conformal minimum variance distortionless response,Distortionlessc MVDR)方法[9]。优化问题及约束条件表述为

式中:min(·)为取最小值函数;E(·)为求数学期望函数;y(n)为输出信号;|·|为取绝对值运算符;w为抽头系数矩阵;wmp为第m个阵元的第p个抽头的权系数,其中m∈{1,2,…,M},p∈{1,2,…,P},P为奇数;H 为矩阵共轭转置运算符;R=E（ZZH）为信号观测向量的自相关矩阵;c为约束向量;cd为信号对应的共形导向矢量。最终抽头系数的最优解

STAP的传递函数

式中:ω为归一化频率;Ts为采样周期;为cd的第m个元素;* 为共轭运算符;wp=[w1pw2p…wMp]为M个阵元的第p个抽头的权系数组成的向量;为第p个抽头的系数。从式(12)的形式可以看出,整个系统的传输函数可以由一个抽头数为P的FIR 滤波器来等效,其中第p个抽头的系数hp由其权系数和信号的共形导向矢量共同来决定。等效FIR滤波器的结构如图1所示。

图1 STAP的等效FIR 滤波器

由式(11)和式(12)可以得到等效FIR 滤波器的系数向量h= [h1h2…hP]T。h关于中间系数共轭对称,则系统可以等价为一个线性相位滤波器,不会引入载波相位偏差,且群延迟为一个与信号来向无关的固定常数(P-1)Ts/2[9]。因此,针对任意方向的北斗信号,经过此系统都会引入一个相同且等于此群延迟的伪码相位偏差,故可以直接补偿掉,不会影响最终的定位结果。补偿后系统的传递函数可以表示为

式中:f为频率;‖·‖为矩阵取模运算符。

1.3 降秩处理

使用一个合适的低维子空间对观测空间进行近似,即降秩处理,可以在保证抗干扰算法性能的同时降低计算量。降秩的广义旁瓣相消架构处理如图2所示。

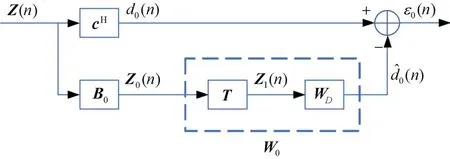
图2 降秩的广义旁瓣相消架构处理

输入信号Z(n)通过上支路后得到含有北斗导航信号的期望信号d0(n)。下支路通过阻塞矩阵B0阻塞上支路信号得到Z0(n),使其仅包含干扰信号。B0=null(c)是通过求解c的零空间得到的阻塞矩阵,其中c是Distortionlessc MVDR 方法中的约束向量。然后Z0(n)通过维纳滤波器W0估计得到对d0(n)的估计0(n)。维纳滤波器W0通过适当的MP×D维降秩转换矩阵T,使输入数据从MP维降低到D维的Z1(n),再通过WD进行自适应加权处理,得到对d0(n)的估计0(n)。最后上下支路相减得到误差信号ε0(n)。WD表示在D维空间内处理的最优权值向量。降秩的MWF则是选择合适的D值,将图2所示分解过程重复D次,此时,降维的观测向量中几乎不含干扰分量,协方差矩阵已趋于白化。对应的降秩矩阵T和WD分别表示为

式中:hi为第i级分解的约束向量;Bi为第i级分解的阻塞矩阵;wi为最优权的第i项。

MWF的过程中没有出现矩阵求逆和特征分解运算,进一步降低了运算复杂度,但仍需计算协方差矩阵和阻塞矩阵。基于此考虑,使用相关相减(correlation subtraction architecture,CSA)的方法产生阻塞矩阵,对算法进行简化,以避开协方差矩阵的计算,同时在分解的过程中通过采样均方误差(SMSE)的比较实现在线秩选。通过对逆向递归的综合滤波器的改进,实现只用一次前向迭代同时完成秩选和滤波器系数求解,降低计算量。上述滤波器称为迭代相关相减多级维纳滤波器(iterative-CSA-MWF,ICSA-MWF),其整体结构如图3所示。

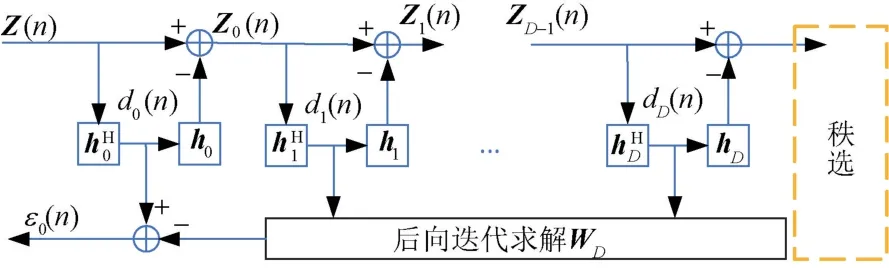
图3 迭代实现的相关相减多级维纳滤波器结构

迭代实现的相关相减多级维纳滤波器算法流程如图4 所示,其中size(·)为获取维数函数,σSMSE为采样均方误差。

图4 迭代实现的相关相减多级维纳滤波器算法流程

2 仿真分析

2.1 参数设置

基于前述信号接收模型,以一种实际工程所使用的带中心阵元的圆柱共形阵列为例,实现抗干扰算法。圆柱共形阵列结构如图5 所示。其中阵元数M=5,圆柱载体半径R=0.1 m,中心阵元p1指向天顶方向(z向),外围阵元p2～阵元p5相对于中心阵元绕圆柱轴线旋转角α=30°,圆柱半长L=0.102 5 m。o1x1y1z1是以p2为原点,圆柱径向为z1向,圆柱轴向为x1向的局部坐标系。

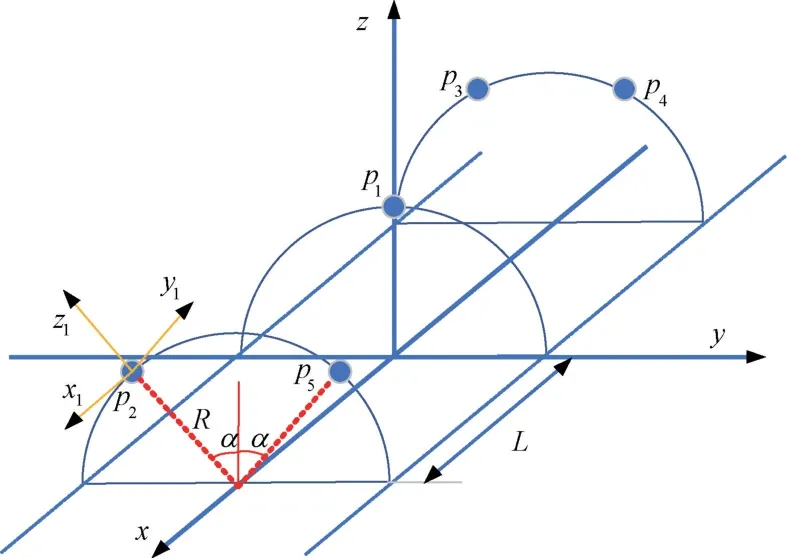
图5 共形阵列的结构图

设时延抽头数P=5。为了更好地展示降秩维数D不同带来的性能差异,使用3个宽带干扰和1 个窄带干扰的配置。其中北斗信号来向为(30°,30°),信噪比为-30 d B;阻塞干扰来向分别为(40°,90°),(60°,180°)和(50°,60°),干噪比均设为70 d B;窄带干扰为单频干扰,频率与北斗信号中心频率相同,来向为(70°,240°),干噪比为70 dB。

2.2 协方差矩阵的特征值

在进行降秩方法性能分析前,应首先对观测向量构成的协方差矩阵的特征值分布情况进行分析,仿真结果如图6所示。其中横轴为按特征值的绝对值大小排序后的特征值编号i,纵轴为特征值的绝对值。可以看到特征值的绝对值大小明显分为两段,曲线段的特征值即为干扰分量所对应的特征值,水平线部分则为噪声对应的特征值。其中,宽带干扰和窄带干扰的特征值分布特征有较大区别:宽带干扰对应的特征值整体较大,窄带干扰则相反,可以从窄带干扰能量更集中的角度来考虑。同时根据多次不同条件下的实验,得出如下经验结论:STAP 观测向量协方差矩阵对应大特征值数目Γ≈NJP,其中NJ即为总的干扰数目。

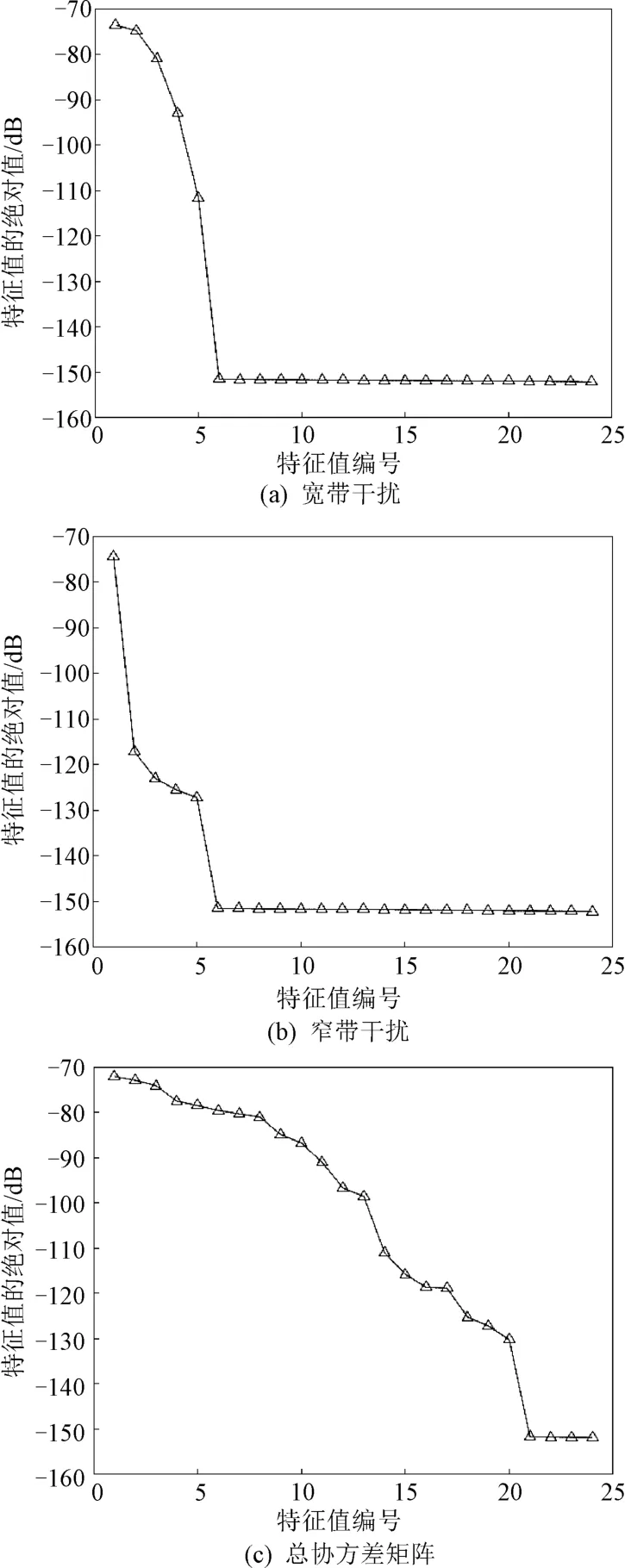
图6 特征值分布情况

2.3 降秩维数D 对抗干扰算法的影响

设定不同的D值进行实验。其中用于对比的PC和CSM 方法,按对应准则取D个特征值和特征向量获得降秩矩阵T;对于ICSA-MWF方法则是设定固定的迭代次数,不再使用SMSE进行秩选。分别从抗干扰性能和保持等效FIR滤波器的线性相位性的能力两方面来进行分析,并取全秩处理时的结果作为对照,标记为Fullrank。4种处理方法在不同快拍数下的抗干扰性能对比结果如图7所示。

图7 降秩维数D 对抗干扰性能的影响

由图7可明显看出,随着降秩维数D的增大,各降秩方法的输出信噪比均逐渐增大,其中D<10的部分因为维数过低导致抗干扰算法几乎失效,参考意义不大。此外,可以看出PC方法的性能相对于另外两种方法较差,较高快拍条件下达到全秩处理时的输出信噪比水平所需降秩维数仍等于观测向量协方差矩阵的大特征值数目Γ(此处Γ=20),明显高于另两种方法。CSM 方法得益于自身的特点,即采用遍历法确定使输出信噪比最大化的D个特征向量,其抗干扰性能优异,且随着快拍数增加,达到全秩处理的输出信噪比水平所需的D值逐渐减小。在快拍数为10 000时,虽然Γ=20,但CSM 方法在D=16时即可达到全秩处理的输出信噪比水平。而ICSAMWF 方法的性能介于PC 方法和CSM 方法之间,且在低快拍时性能仍较好。

降秩处理的本意就是为了降低运算复杂度,提高算法实时性。CSM 方法虽然性能较好,但其引入了过多的额外计算量,与降秩处理的本意相悖。ICSA-MWF 方法省去了协方差矩阵的计算及其特征分解,且可以通过一次前向迭代实现自适应秩选、降秩矩阵计算和降秩权值计算,大大降低了STAP 算法实现的复杂度。因此本文认为ICSA-MWF 是更为合适的降秩方法。

选取几个关键D值,通过仿真信号群延时,分析上述各降秩方法对于Distortionless-c MVDR算法的线性相位特性的影响,仿真结果如图8所示。

图8 降秩维数D 对群延迟的影响

由图8可知,当D=10时,降秩维数过低,不仅抗干扰性能差,抗干扰算法的群延迟波动也较大,线性相位特性不理想。当D=16 时,CSM、ICSA-MWF和Full rank 曲线几乎重合,CSM方法的输出信噪比已经接近全秩处理水平,算法也接近线性相位系统,ICSA-MWF 方法抗干扰性能虽未达到最佳,但已可以保持较理想的线性相位特性。当D=Γ=20时,各方法均接近线性相位系统,其中ICSA-MWF和Full rank 曲线几乎重合。

经过本小节的分析,说明了上述降秩方法取合适的D值时,既可保证输出信噪比的水平,也可以保证Distortionless-c MVDR 算法的线性相位特性。再综合各算法的计算复杂度,ICSAMWF 是最为适合的降秩方法。

3 结论

本文提出了一种针对无失真空时共形MVDR 算法的降秩处理方法。该方法结合了相关相减方法和对逆向递归的综合滤波器的改进,规避了协方差矩阵的计算,实现了在线秩选以及只用一次前向迭代同时完成秩选和滤波器系数求解,极大地降低了计算量。仿真结果表明,当取合适的D值时,既可保证输出信噪比的水平,也可以保证Distortionless-c MVDR 算法的线性相位特性,减小处理过程对卫星信号产生的畸变影响。