亲历建模过程 培养模型意识

【摘 要】除法竖式的“长相”比较特别，计算步骤比较多，学生理解算理不易，掌握算法更难。借助拟人化的方法让除法竖式变成一座有趣的“工厂”，借助分一分、画一画等直观操作使算理一目了然，借助比划、横式、口诀、儿歌等多元表征使算法呼之即出，借助由易到难的分层练习让计算模型真正内化，将有助于学生在亲身体验、探究、运用中逐步建构出除、乘、减的计算模型，从而促进他们有效培育数感、运算能力、模型意识等核心素养。

【关键词】小学数学；除法竖式；建模；模型意识

【中图分类号】G623.5  【文献标志码】A  【文章编号】1005-6009（2023）09-0075-05

【作者简介】冯桂群，江苏省南通师范学校第一附属小学（江苏南通，226001）教师，南通师范高等专科学校小教研究所研究员，正高级教师，江苏省数学特级教师。

苏教版数学教材将“除法竖式计算”的起始课安排在二年级下册。与加、减、乘这三种运算相比，除法竖式的计算流程最复杂——涉及除、乘、减三种运算，算理理解起来也不太容易；同时，除法竖式“长”得跟加法竖式、减法竖式完全不一样，难以引发直接的正向迁移，这些构成了学生学习过程中的认知障碍。《义务教育数学课程标准（2022年版）》指出：教学活动应注重启发式，激发学生学习兴趣，引发学生积极思考， 鼓励学生质疑问难，引导学生在真实情境中发现问题和提出问题，利用观察、猜测、实验、计算、推理、验证、数据分析、直观想象等方法分析问题和解决问题……逐步形成核心素养。为了有效落实新课改理念，笔者精心创设循序渐进的探究情境和活动，让学生在亲身体验、探究、运用中逐步建构“除、乘、减”三步计算模型，从而有效提升他们的运算能力、模型意识等核心素养。

一、激活经验，变式导入

师：我们先来玩个拨数游戏。瞧！这是计数器，谁来拨出数11？（指名一生上台拨数）计数器上这两个1的含义一样吗？为什么？

生：左边的1在十位上，表示一个十；右边的1在个位上，表示一个一。

师：讲得真好！同样的数字在不同的数位上，表示的数值不一样。

师：在个位上添上一个拨珠，就得到了12。列竖式计算12-4时，要将4和12中的几对齐，为什么？（师板演，指名一生口答）

生：4要和12个位上的2对齐，因为2和4的计数单位相同，都是一。

师：是呀，相同数位对齐，能方便地将计数单位相同的数直接相加减。所以，列加减竖式时，一定要注意相同数位——对齐。

师：老师要变魔术了！想象一下，在减号上下各添一个点，12-4就变成12÷4。计算12÷4，也可以列竖式呢！关于除法的竖式计算，你想研究哪些问题？

生1：除法竖式跟加减法竖式“长”得一样吗？

生2：列除法竖式也要相同数位对齐吗？

生3：列除法竖式要注意什么？

…………

师：孩子们真善于提问！让我们带着这些问题一起走进今天的数学乐园吧！

约翰.D.布兰思福特等人在《人是如何学习的：大脑、心理、经验及学校》一书中指出：有许多证据表明，如果教师关注学习者带到学习任务中的已有知识和观念，将这些知识当作新教学的起点，并在教学过程中监控学生概念的转化，那么就可以促进学生学习。在上述教学中，教师借助拨数和列减法竖式，无痕地激活学生的已有学习经验，强调关注数位和相同数位对齐的重要性，为他们后续学习除法竖式埋下了伏笔。同时，借助有趣的数学魔术，让学生意识到符号间的内在联系，并自然地由减法竖式引出除法竖式，在类比中激发他们的好奇心与问题意识，使他们在主动提问中兴趣盎然地步入新知探究之旅。

二、深度探究，建构模型

师（出示例3第一小题）：请看，这位妈妈是如何分苹果的？第一个问题是什么？

生：妈妈把12个苹果每4个放一盘，问题是“可以放几盘？”。

师：在头脑里想象一下分苹果的情景，结果是多少？如何列式？

生：12÷4=3（盘）。

师：借助哪句口诀，就能直接口算出12÷4的得数？

生：三四十二。

师：除了借助乘法口诀直接口算，还可以用除法竖式来计算。不过，除法竖式“长”得跟加减法的竖式完全不同，学起来有些困难，敢于挑战吗？

生（齐）：敢！

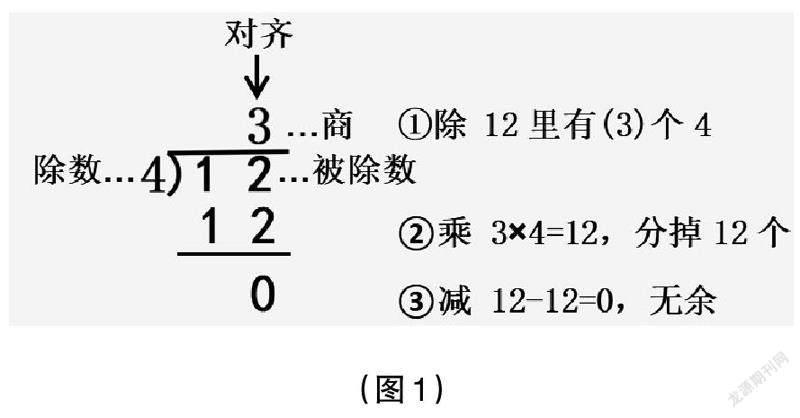
师：仔细看，除号中的两个点要变魔术了！（多媒体同步演示）这两个点很顽皮，它们伸出弯弯的手臂，手拉手跑到除号中横线的前方，变出了汉字“厂”！在这个神奇的竖式“工厂”里，被除数、除数和商各就其位，被除数12站在“厂”里，等待被平均分；除数4站在“厂”的左侧，提醒大家要4个4个地分；而除得的商3特别顽皮，竟爬到“厂”的上面，对着被除数的个位玩起“叠罗汉”的游戏。为什么商要跟12的个位而不是十位对齐呢？

生1：因为3表示3个一，所以要跟12的个位对齐。

生2：这跟加法和减法竖式中相同数位对齐的道理是一样的。

师：真会思考和联想！除法竖式跟加法和减法竖式最大的共同点就是——除了除数，其他数在竖式中都要做到“相同数位对齐”，这一点大家要特别注意。除法竖式的第一步就是“除中求商”。（同步板书）

生：老师，商不是求出来了吗？

师：真善于提问！这就是除法竖式的特殊之处。写12÷4的除法竖式时，不仅要算出除得的商“3”，还要表示平均分时一共分掉了几个4，最终有没有剩余。请大家仔细观察和思考分苹果的过程。（多媒体动态演示将12个苹果每4个放一盘的完整过程）

生：一共分掉了3个4，最后没有剩余。

師：既然分掉了3个4，那一共分掉了多少个苹果，怎么求出来？

生：一共分掉3×4=12（个）。

师：对！除法竖式的第2步就是通过“乘”求分掉的苹果。一共12个苹果，分掉了12个，最后剩几个，如何算？

生：12-12=0（个），分完了，没有剩余。

师（完善板书后得到图1）：仔细观察，12÷4的除法竖式包括哪三步？

生：除、乘和减。

师：这三步分别求什么？

生：通过除，求得商是3，表示3盘；通过乘，求出一共分掉12个苹果；通过减，求出最后剩余0个，也就是无余。

师：真会总结！除法竖式比加法和减法竖式复杂，不但要注意商的个位跟被除数的个位对齐，还要按除、乘、减三步来分别求出商是几、一共分掉几和最后剩余几。

借助变魔术游戏，完全陌生的竖式“脸谱”变得熟悉可亲——有趣的除号瞬间变为竖式中的“工厂”，商跟被除数竟在“工厂”上下玩起了相同数位对齐的“叠罗汉”游戏；求出商后，还得在竖式里分别表示出一共分掉和最终剩余的数量。在动态演示、师生互动、用心观察、缜密思考和简洁表达的过程中，算理和算法被完美地创生出来，“除、乘、减”三步流程一清二楚，数学思维的严谨之美、逻辑之美与简约之美也展现无遗。

师：如果将这12个苹果每5个放一盘，结果怎样？先在头脑里想象出平均分的过程和结果，再在研究单上圈一圈、画一画。（学生自主圈、画）对不对呢？一起看屏幕！（多媒体动态演示将12个苹果每5个放一盘的完整过程）结合分苹果的具体过程和图画，你也能用除、乘、减这三个步骤列出12÷5的除法竖式吗？先独立思考并完成研究单，然后在四人小组里交流，做好上台展示的准备。

生在独立思考与小组交流中完成如图2所示的研究单，之后指名某小组上台展示。

师：孩子们真能干！通过独立思考、小组合作和全班交流，学会了有余数的除法的竖式计算。比较12÷4和12÷5的竖式，它们有什么相同点和不同点？

生1：相同点是都要按除、乘、减这三个步骤来计算。

生2：商的個位都要和被除数的个位对齐。

生3：不同点是一个无余，一个有余。

师：在第二步“乘”的时候，都是用除法竖式中的什么数相乘的？

生：“商”乘“除数”。

师：下面这首儿歌，你能迅速填写完整吗？

生边拍手边和师对口令。

师：除法竖式分几步？

生：（除）（乘）（减），共（三）步！

师：第二步，谁乘谁？

生：（商）乘（除数），要记住！

在探究有余数的除法竖式时，教师通过开展观察、想象、画图等自主探索、合作交流活动，提供填空式的思考支架，由扶到放地让学生在类推中学会用竖式计算12÷5，感受12÷5跟12÷4在算法和算理上的一致性；之后，借助反思与总结，进一步抽象、概括算法，在说唱儿歌的过程中实现数学学习的趣味化表达，深入浅出地实现计算模型的整体建构，发展了学生的数感、运算能力、推理意识和模型意识，为他们后续学习更复杂的除法笔算打下了坚实的认知基础。

三、分层巩固，内化模型

师：下面，我们来玩两个手势游戏。听好——将9根棒平均分成2堆，每堆几根，余几根？请同桌两人在想象与合作中比划出最终的结果。

生与同桌合作开展比划游戏，师巡视指导，后指名回答。

生：9根棒平均分成2堆，每堆4根，最后剩余1根。

师：真不错！我们来加大难度，听好——将11根棒每4根一堆，分成几堆，余几根？合作比划游戏开始！

生与同桌合作开展比划游戏，师巡视指导，后指名回答。

生：11根棒每4根一堆，分成2堆，余3根。

师：孩子们比划得好，说得更棒！那你能结合手势游戏，用除法竖式快速求出9÷2和11÷4的结果吗？

生独立完成“想想做做”第1题，师巡视指导后组织交流。

师：千金难买回头看！仔细观察这两个竖式，你能找出它们的共同点吗？

生1：都是用除、乘、减三个步骤算出来的。

生2：都有余数。

生3：第二步算出的积都是8。

师：真善于观察和表达。这两题不仅第二步的乘积一样，还用了同一句口诀——

生（齐）：二四得八。

师：可见，除了借助动手分一分、画一画和比划手势以外，我们还可以通过念口诀，快速求出竖式计算中第一步的商和第二步的积；在被除数较大的情况下，用口诀来求这里的商与积，会特别简便。比如4[24]和4[25]，都可以共用哪句口诀求商？

生：四六二十四。

师：25里最多有6个4吗？为什么不是7个4？

生：四七二十八，28超过25了，商大了。

师：念口诀求商时，不妨往上多念一句，发现积超过了被除数，再退回来，这就叫——进退自如。只有找对除得的商，后面的乘中求积和减中求差才能顺利进行。

师：继续变魔术！将24变为23，23÷4还跟２4÷4和25÷4共用“四六二十四”求商吗？

生1：不能！四六二十四，超过23了，退一步，四五二十。

生2：四五二十，商是5，乘得的积是20，减得的差是3，余数就是3。

师：真会思考！那5[30]和5[28]分别念哪句口诀，就能快速求出相应的商、积和差？独立完成，写出相应的横式，并跟同桌交流。

生独立完成后组织交流。

师：写这两题的横式时，要注意什么？

生：30÷5=6，没有余数；28÷5=5……3，要记得商后写上余数3。

师：把刚才的注意点总结到数学儿歌里去，一起大声说一说！

生（齐）：除法竖式分几步？（除）（乘）（减），共（三）步！第二步，谁乘谁？（商）乘（除数），要记住！横式得数写清楚，无余时，只写（商）；有余时，添（余）数，添——（余）——数！

师：你们能用所学的计算本领解决实际问题吗？请看书上第5页的4、5两题，同桌两人各选其中一题来完成，之后相互交流，做好上台展示的准备。

…………

师：在解决有余数的实际问题时，除了要正确列竖式计算以外，还需要注意什么？

生：横式得数中的两个单位名称要写对，答句里商和余数的结果也要写全。

师：真会反思！

在以上递进练习中，教师先引导学生借助有趣的手势游戏完成基础练习，培养他们的合作能力，同时利用直观操作，使直观的算理与抽象的算法相得益彰；之后顺势引导学生用较抽象的乘法口诀直接求商和积，让计算思路由直观走向抽象、由感性走向理性、由具象表征走向符号表征，从而有效培养学生的运算能力和推理意识；最后在分工合作中学以致用，提升学生解决实际问题的能力，促进他们养成严谨解题、自觉反思的习惯。

四、拓展思路，发展模型意识和创新意识

师：通过今天的学习，你有哪些新的收获？

生1：除法竖式的确有些复杂，要分除、乘、减三步。

生2：在除法竖式中，商的个位要和被除数的个位对齐。

生3：念口诀求商时可以往上多念一句，积超过被除数了就再退一步，这样求得的商刚好。

生4：除了竖式，有余数的除法的横式要记得写全商和余数，解决实际问題时还要记得写对单位名称。

师：孩子们真是反思、总结的小达人！

师：这里有一个没写全的除法竖式（如图3），你能用今天学到的本领把它补全吗？想好一种填法就在四人小组里交流，看哪一组能想到与众不同的思路。

小组交流后组织全班互动。

生：第二步乘积个位上是4，我想到口诀“二七十四”，如果商是7、除数是2，余数就是1，被除数就是14加1等于15。

师：真善于观察！如果除数是7而商是2，余数可能是——

生：余数可能是1到6，那被除数就可能是15到20。

师：数感极好。除了“二七十四”，你还能想到哪几句口诀？

…………

师：这是一道开放题，答案有很多种。孩子们课后可以继续思考与探讨。

通过组织对全课进行总结与反思，让他们有“登高望远”的整体感和成就感，形成“除、乘、减”三步流程的整体架构，培养元认知能力和学好数学的信心。之后的拓展练习创设了一个极其开放的思维空间，让学生在迁移和运用中敏锐地观察、灵活地思考、有序地表达，学会求异思维、有序思维、逆向思维等， 同时使数学教学真正进入启智增慧、创新育人的美好境界。