带划痕缺陷的碳纤维增强树脂复合材料疲劳寿命研究

张学薇,汪振兴,吴堂珍,龚明程

(中国直升机设计研究所,江西 景德镇 333001)

0 引言

纤维增强复合材料具有卓越的拉伸强度性能、抗冲击性能和断裂韧性,广泛应用于航空航天、交通、可再生能源等领域[1]。然而,在材料制造和维修过程中常常会引入缺陷,甚至出于功能需求,人为引入孔槽、切口等,这些缺陷大大影响了材料的强度和疲劳寿命。

由于复合材料自身的破坏机制复杂,如何可靠地评估缺陷对材料性能的影响是一大挑战。目前已有的剩余强度模型需要基于大量的试验获取的剩余强度数据。由于疲劳损伤的复杂性,如何建立物理损伤模型,以满足各关键参数对损伤过程的影响,仍是亟待解决的问题。

同时,研究表明,划痕类型(单边缺口[2]、双边缺口[3]、中心圆孔[4-5])及划痕参数(缺口尺寸、缺口形状)[5-6]对静态载荷和疲劳载荷下含划痕纤维增强复合材料层合板的力学性能影响极大,损伤失效模式取决于纤维类型、基体韧性、铺层次序、载荷类型等因素。目前大部分研究都是针对中心圆孔缺陷展开的,针对缺口的极少,尤其是双边缺口,且少有文章开展缺口处疲劳载荷作用下的寿命和行为研究。因此,本文通过详细的理论计算,针对不同载荷条件和划痕参数,展开双边缺口对纤维增强复合材料疲劳寿命的影响研究,并通过试验验证理论的正确性。

1 划痕缺陷容限渐进损伤分析方法

1.1 疲劳寿命理论分析

考虑复合材料性能固有的复杂性,难以采用单一变量定义复合材料损伤,本文采用非线性二次函数作为损伤函数,建立疲劳加载循环次数n与最大疲劳应力s、加载频率ω、应力比r、强度极限R0、剩余强度R(n)的关系:

n=f(s,ω,r)[R0-R(n)]q

(1)

其中,q为模型参数。式(1)表明了恒定应力水平与恒定加载频率下复合材料的强度降。

对于给定的加载频率ω和应力比r,有f(s,ω,r)=f(s)=C(s-S0)p,则式(1)改写为[7]:

n=C(s-S0)p[R0-R(n)]q

(2)

其中,C和p为模型参数,s为疲劳强度,S0为拟合疲劳极限。

当指定失效状态,即疲劳剩余强度R(n)等于疲劳应力S时,式(2)变为S-N曲线:

N=C(S-S0)p(R0-S)q

(3)

当指定加载应力s=St时,式(2)退化为R-n曲线:

n=C(St-S0)p[R0-R(n)]q

(4)

根据定量方程随机化方法,对式(2)随机化,并取对数,得到:

Y=a0+a1x1+a2x2+U

(5)

其中,Y=lgn,a0=lgC,a1=p,a2=q,x1=lg(s-S0),x2=lg[R0-R(n)],U=lgX(n),U～N[0,σ2]。由式(5)可知,Y～N[a0+a1x1+a2x2,σ2],根据极大似然估计方法,可以得到:

(6)

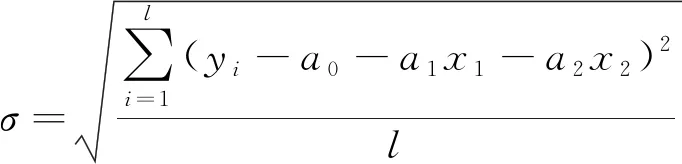
(7)

其中

(8)

因此,可以得到模型参数C、p和q:

p=a1

q=a2

(9)

1.2 考虑缺陷尺寸效应的疲劳寿命理论分析

考虑缺陷尺寸对复合材料的疲劳剩余强度模型参数有显著影响,复合材料的拟合疲劳极限和初始剩余强度随缺陷尺寸的变化而变化,因此对上节模型进行修正:

(10)

将式(10)代入式(2),建立考虑缺陷尺寸效应的疲劳剩余强度模型,得到s-n-R-d疲劳剩余强度模型在给定应力比r下的控制方程[8]:

n=

(11)

其中,C、p、q为考虑缺陷尺寸效应的归一化模型参数。

考虑疲劳极限,对式(10)取对数,得到:

Y=a+bx

(12)

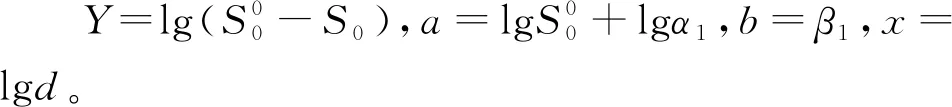
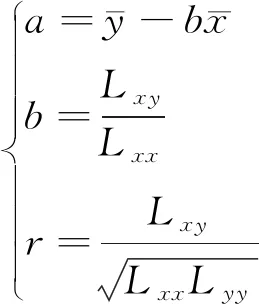
(13)

其中

(14)

β1=b

(15)

1.3 有限元分析方法

将式(2)变换,得到n次疲劳循环后的材料剩余强度R(n):

(16)

并得到一次疲劳循环导致的剩余强度降ΔR(n):

(17)

在有限元计算过程中,材料单元的剩余强度随着循环的增加逐渐下降。第1个单元在M1个载荷循环后的剩余强度为:

(18)

式中,ΔR1(j)为第1个单元在第j次循环强度的剩余强度降,R0为单元的初始剩余强度。此时,载荷循环次数为T0=M1。

当R1(T0)≤[S1]max时,第1个单元发生失效,此时,第i个单元的剩余强度为:

(19)

式中,ΔRi(j)为第i个单元在第j次循环强度的剩余强度降。

以此类推,循环到第i个载荷循环块Mi时,第k个单元的剩余强度为:

(20)

此时,载荷循环次数为:

(21)

当Ri(T0)≤[Si]max时,第i个单元失效,第k个单元的剩余强度为:

(22)

在疲劳渐进损伤分析过程中,采用式(17)和式(20)计算复合材料结构各个单元的强度衰减和剩余强度,式中参数由试验测定的剩余强度模型确定。利用ANSYS有限元软件,按照材料属性、试样尺寸和缺陷类型,完成层合板建模,然后在给定载荷值下进行有限元应力计算。根据剩余强度准则,当满足Ri(T0)≤[Si]max时,判断单元是否失效。若无单元失效,则更新所有未失效单元的剩余强度,并增加1次循环次数,再次根据剩余强度准则判断单元是否失效,如此循环直至有单元发生失效;若有单元失效则杀死单元,并更新未失效单元的剩余强度,增加1次循环次数,重新在给定载荷值下进行有限元计算,如此循环直至结构发生最终破坏,得到复合材料结构剩余寿命。

2 试样及测试手段

2.1 材料与试样

本文采用3238A/CF3052碳纤维增强树脂复合材料;划痕深度分别为2,3,4 mm,应力比r=0.05;四级不同的疲劳循环加载次数,包括N=104,105,5×105,106。划痕及材料尺寸如图1所示。

图1 带划痕的试验件(单位:mm)

2.2 测试方法

按照ASTM标准试验方法D5766-11和D6484-09,在MTS-880-100 kN和INSTRON-8801-50 kN疲劳试验机上完成试验。疲劳加载波形为正弦波,加载频率f=10 Hz,试验环境为大气、室温。根据ASTM标准试验方法D7615-11和E739-10,拉伸疲劳加载的应力比为0.05,得到划痕缺陷下的模拟件缺陷容限性能曲线。

3 疲劳数值模拟与试验验证

3.1 疲劳剩余强度曲面

表1列出了3238A/CF3052碳纤维增强树脂复合材料的基本力学性能。对图1所示材料试件,按照2.2节测试手段得到含不同缺陷尺寸的复合材料的剩余强度,如表2所示。

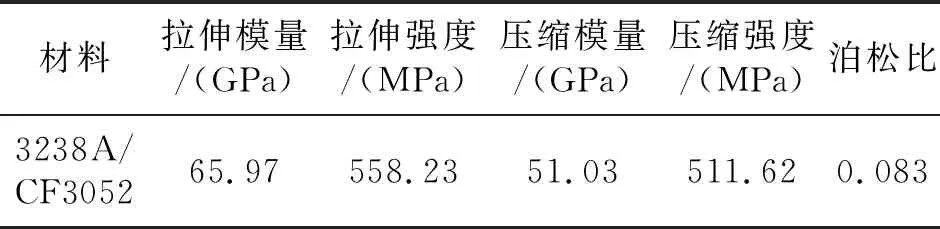
表1 3238A/CF3052复合材料基本力学性能

表2 含缺陷3238A/CF3052复合材料剩余强度

根据上述材料参数,按照式(2)建立n-s-R控制方程,如表3所示,按照式(11)建立考虑尺寸效应的n-s-R-d控制方程,如表4所示。

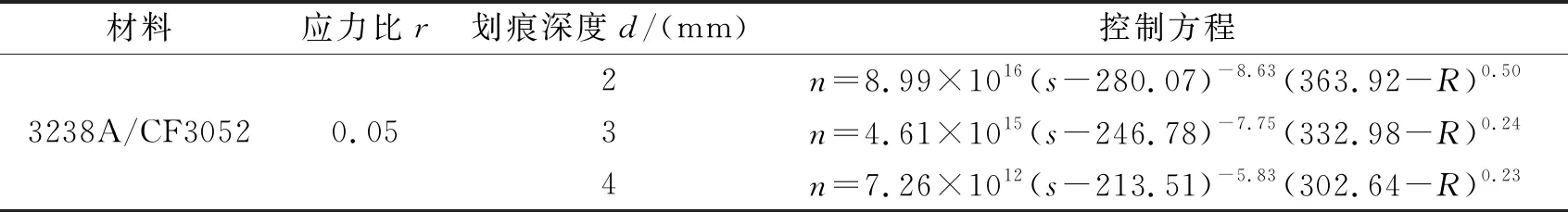
表3 未考虑尺寸效应的划痕缺陷复合材料疲劳寿命

表4 考虑尺寸效应的划痕缺陷复合材料疲劳寿命

将上述模拟结果绘制成疲劳剩余强度曲面,建立应力比为0.05时不同划痕深度下最大疲劳应力s、剩余强度R(n)、疲劳循环次数N的关系,如图2所示。

对比同一种模型同一应力比下的曲面,如图2(a),发现划痕缺陷的存在会大大降低材料的疲劳剩余强度,且剩余强度随划痕深度的增大而降低。同时,考虑尺寸效应时各参数的变化规律与之前一致,如图2(b)。由于碳纤维和基体之间的刚度不匹配程度更高,且碳纤维与树脂基体的界面结合较差,因此划痕处应力集中现象明显,导致整体强度偏低。

图2 复合材料(3238A/CF3052,R=0.05)疲劳剩余强度曲面

3.2 试验与模型验证

从图3中可知,划痕缺陷的存在会大大降低材料的疲劳寿命,相同疲劳循环加载次数下,材料所能承受的最大疲劳应力降低十分明显。以3238A/CF3052碳纤维复合材料拉-拉测试结果为例,如图3(a):当划痕深度为2 mm时,在相同疲劳寿命下,所能承受的最大疲劳应力降低20%以上,当划痕深度为4 mm时,最大疲劳应力降低35%以上;当最大疲劳应力取350 MPa时,无划痕缺陷材料的疲劳寿命达106,而有划痕缺陷材料疲劳寿命不足104。

此外,对考虑尺寸效应的疲劳寿命理论,将试验数据与模拟曲线绘制如图3(b),图中虚线表示考虑尺寸效应的模拟曲线,同样发现符合程度良好,测量结果在模拟曲线两侧均匀分布,表明所提出的考虑尺寸效应的模型能够较好地预测材料疲劳寿命。

图3 复合材料(3238A/CF3052,R=0.05)S-N曲线

3.3 数值模拟计算

在ANSYS中建立的3 mm划痕深度缺陷层合板有限元模型如图4所示。单元类型采用SOLSH190,网格尺寸设置为1.5 mm,层合板左端施加固支约束,下端施加对称约束,右端施加最大疲劳载荷值。按照1.3节有限元计算方法,对3238A/CF3052碳纤维复合材料划痕缺陷层合板进行拉-拉疲劳有限元仿真计算,得到层合板渐进损伤过程如图5,应力分布对比见图6。由图可知,疲劳损伤从边缘划痕处萌生并横向扩展,直至层合板发生最终失效。

图4 3 mm划痕缺陷层合板疲劳有限元建模结果

图5 3238A/CF3052 3 mm划痕缺陷拉-拉疲劳渐进损伤过程图

图6 3238A/CF3052 3 mm划痕缺陷疲劳破坏前后应力分布对比

将复合材料划痕缺陷层合板疲劳寿命试验疲劳寿命数据与有限元计算疲劳寿命数据进行对比,并对有限元计算结果进行数据拟合,得到有限元模拟疲劳S-N曲线,与试验数据及原拟合结果进行对比,如图7所示。

由图7可以看到,有限元模拟结果与试验结果吻合良好,两者曲线非常接近,最大偏离误差不超过23%,且随着划痕深度的增加,疲劳S-N曲线性能降低,符合实际情况。

模拟结果与试验数据存在一定偏差的可能原因是试验结果存在分散性及剩余强度疲劳性能模型难以表征复合材料内部复杂的损伤机制。事实上,含有相同缺陷的相同复合材料试样,在疲劳过程中的损伤模式和机制也存在分散性。有限元渐进损伤模拟难以区分和识别这些模式和机理,会导致一定的计算偏差。因此,我们的模型和计算能够较好地模拟实际情况,预测材料的疲劳寿命。

4 结论

本文针对3238A/CF3052碳纤维增强树脂复合材料,首先提出了含有划痕缺陷的材料疲劳寿命理论,并提出了考虑尺寸效应的修正公式。通过试验结果以及对疲劳寿命-应力-强度曲面及S-N曲线的分析,研究两种不同材料在不同划痕深度下的疲劳强度和疲劳寿命。同时,利用试验结果与模拟结果的对比,验证所提出理论的正确性,并得到如下结论:

1)随着划痕缺陷深度的增加,材料的剩余强度明显下降。

2)小尺寸划痕情况下,碳纤维复合材料的剩余强度仍较高,而达到一定尺寸时,碳纤维复合材料强度缩减加剧,更容易减少材料使用寿命及产生破坏。

3)利用ANSYS有限元软件进行仿真模拟,结果表明划痕缺陷层合板疲劳寿命有限元计算结果与试验结果吻合良好,相对偏差不超过23%,具有足够精度;计算S-N曲线与试验S-N曲线非常接近,能从计算模拟结果反映出真实试件的疲劳寿命,可以为复合材料的寿命预测提供指导。