无人直升机桨毂RCS影响计算分析与优化

顾浩涵,姜乃文,冯维超

(中国直升机设计研究所,江西 景德镇 333001)

0 引言

随着无人机技术的发展,越来越多的无人直升机问世,多款型号已进入战场经受考验。同有人直升机相比,无人直升机具有使用成本低、安全性较高、环境与任务适应性强的优点。通过变更任务功能载荷,无人直升机可执行物资运输、通讯中继、侦查搜索及攻击等任务,应用前景十分广阔,受到了世界各主要军事强国的重视。而电子技术的发展又使各种现代化防空探测设备和武器的性能不断提升,无人直升机的作战环境变得更加严酷复杂。其飞行高度低、速度慢及敏捷性相对较差的特点,使其容易受到地面和空中武器的探测与攻击。

相比于常规有人直升机,无人直升机机身造型通常更加简洁,但受旋翼系统构型影响,桨毂的外形与结构复杂度仍然较高,对全机雷达散射特性的影响较大。本文采用RCS(雷达散射截面)仿真方法,针对桨毂雷达散射特性及其对无人直升机RCS的影响开展计算分析,并根据结果对桨毂进行了RCS缩减优化。

1 RCS计算方法

随着现代计算技术的进步,现代电磁学发展出了多种求解目标RCS的算法,主要分为两类:时域方法与频域方法。典型的时域方法有FETD(时域有限元法)和FDTD(时域有限差分法);典型的频域方法包括MOM(矩量法)、MFMM(多层快速多极子法)以及高频算法如GO(几何光学法)、PO(物理光学法)、RLGO(射线发射光学法)和UTD(一致性几何绕射法)等等[1]。不同的计算方法通常针对不同的目标或需求,各自存在优缺点。在计算目标雷达散射特性时,需要综合考虑目标种类与散射类型,权衡计算精度与计算资源,选择适当的RCS数值计算方法。

FETD方法采用非结构网格离散计算域,对于一般曲面外形拟合度较好,但随着目标外形复杂度与精细度上升,其效率与误差问题逐渐明显[2]。FDTD方法作为典型的时域算法,将偏微分方程用离散差分方程代替,求解简单快速,但对电大尺寸复杂曲面的模拟较差,影响求解精度[1,3]。

MOM方法是一种严格数值方法,可以求解任意外形的复杂目标,能够精确模拟电流分布,计算精度高,但其计算量巨大,计算资源要求很高[1,4]。MFMM方法作为MOM方法的改进方法,采用逐层嵌套,减少了计算时间,但精度也受到影响,对腔体结构模拟较差,相比高频算法仍需较多的计算资源。

GO方法计算原理简单,但仅适用于简单外形,对于复杂外形的精度计算无法保证,局限性过大。PO方法通过感应场近似积分求解散射场,解决了GO方法对外形的限制问题,计算时间快,资源消耗少,但忽略了多次反射绕射,对于多边缘、强耦合目标会产生较大误差[1,5]。RLGO方法相比于GO方法与PO方法,对复杂曲面外形的适应性更强,且引入了射线多次反射计算与边缘绕射,精度提升且计算效率高,适合方案阶段的快速设计与评估。UTD方法相比于GO方法与PO方法,增加了几何绕射理论,主要针对边缘、尖点以及圆角的绕射计算需求[6]。RLGO方法相比UTD方法对复杂曲面外形的适应性更强,相比GO方法与PO方法,又引入了射线与多次反射计算与边缘绕射,精度提高且计算效率高,适合方案阶段的快速设计与评估。

综合上述对比,对于典型电大尺寸、外形曲面相对复杂、多种雷达散射机理并存的桨毂和桨毂机身组合体的快速计算评估,本文选择RLGO方法进行RCS仿真求解。

2 计算方法验证

为验证本文选取的RCS计算方法的准确性,选取直升机与桨毂常见的典型散射源角反射器作为算例,对三角形三面角反射器与正方形三面角反射器进行了外形建模、网格划分与RCS仿真计算。两种算例的几何参数见表1,外形与网格划分如图1所示。

表1 算例几何参数

图1 两种角反射器计算网格

采用“RLGO+UTD”方法,分别计算两种算例在6 GHz平面波HH极化的RCS,得到随入射角变化的雷达散射曲线,如图2与图3。

图2 三角形角反射器RCS曲线

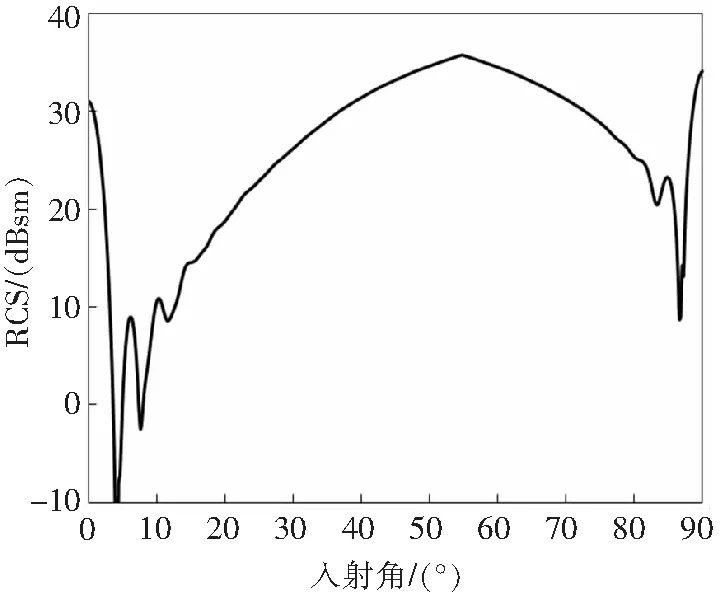
图3 正方形角反射器RCS曲线

从两种算例RCS曲线可以看出,其后向雷达散射的主瓣较宽阔平坦,起伏趋势符合角反射器的雷达散射特性。

对于三角形三面角反射器,式(1)为理论最大散射截面公式[7],其中a为三角形直角边长,λ为工作波长。利用该公式得到的主板峰值为26.22 dBsm;图2中通过仿真计算得到的主板峰值为26.67 dBsm,符合性较好。

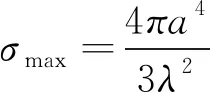
(1)

对于正方形三面角反射器,式(2)为理论最大散射截面公式[1],其中a为正方形边长,λ为工作波长。利用该公式得到的主板峰值为35.76 dBsm;图3中通过仿真计算得到的主板峰值为35.77 dBsm,符合性较好。

(2)

可见本文选用的RLGO仿真算法,可以较好地反映出直升机与桨毂典型散射源角反射器的雷达散射特性。

3 常规桨毂RCS影响计算分析

本文选取一个具有低阻特性的无人直升机机身与常规桨毂外形,依照上述方法进行网格划分与RCS仿真计算。直升机机身与桨毂网格划分如图4、图5所示。其中常规桨毂由于组件数量庞多且细小复杂,因而进行了适当简化。外形主要尺寸参数见表2。

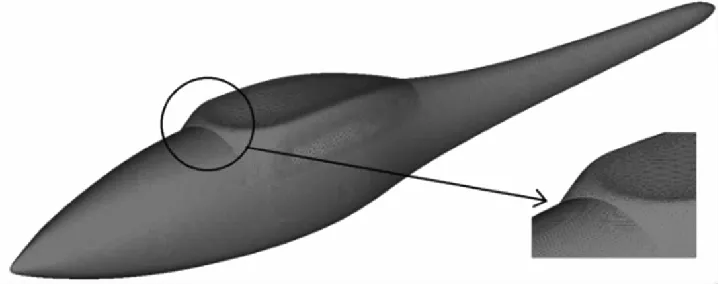
图4 无人直升机机身整体与局部网格划分

图5 常规桨毂简化模型网格划分

计算机身外形在水平入射的6 GHz平面波HH极化与VV极化下的RCS,得到随入射角方位变化的雷达散射特性如图6,并给出了头向、左侧、右侧与尾向四个主要角域±30°的RCS均值见表3。

图6 机身HH/VV极化RCS曲线

表3 机身主要角域RCS(单位:dBsm)

无人机机身整体RCS曲线相对机身纵向对称面呈现出良好的对称性。从RCS曲线与主要角域RCS均值可见,由于机身为细长光滑的低阻流线外形,其头向与尾向RCS均很小;而在侧向,由于机身和动力舱的外形相对入射波接近垂直反射,RCS大幅超出头向与尾向35 dBsm以上。

对于做周期旋转运动的桨毂,本文选取一个桨叶支臂朝前的典型状态,计算常规桨毂外形在水平入射的6 GHz平面波HH极化与VV极化下的RCS,得到随入射角方位变化的雷达散射特性如图7,并给出了头向、左侧、右侧与尾向四个主要角域±30°的RCS均值(见表4)。

图7 常规桨毂HH/VV极化RCS曲线

表4 常规桨毂主要角域RCS(单位:dBsm)

从RCS曲线与主要角域RCS均值可见,常规桨毂由于布局与结构的特点,其RCS也表现出明显的周期性与对称性。由于桨毂存在大量的水平与垂直方向的圆柱形或圆台形结构,以及多个组件构成的大量三面角反射器,造成雷达散射较强烈,其在头向与尾向的RCS均值甚至超出了无人机机身自身近15 dBsm。

将无人机机身与常规桨毂组合,同样选择一个桨叶支臂朝前的桨毂典型状态进行组合体网格划分如图8。

图8 机身+常规桨毂组合体网格划分

采用本文方法求解“机身+常规桨毂”组合体在水平入射的6 GHz平面波HH极化与VV极化下的RCS,得到随入射角变化的雷达散射特性如图9,并给出了头向、左侧、右侧与尾向四个主要角域±30°的RCS均值(见表5)。

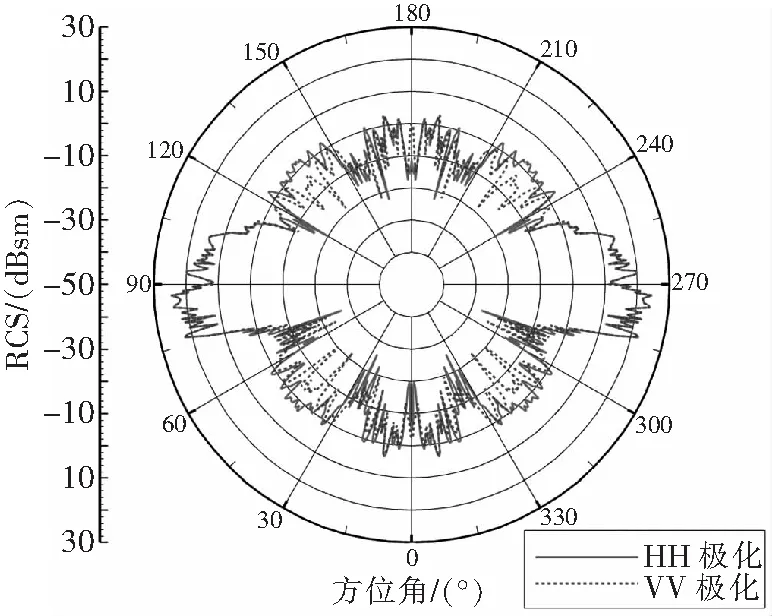
图9 机身+常规桨毂HH/VV极化RCS曲线

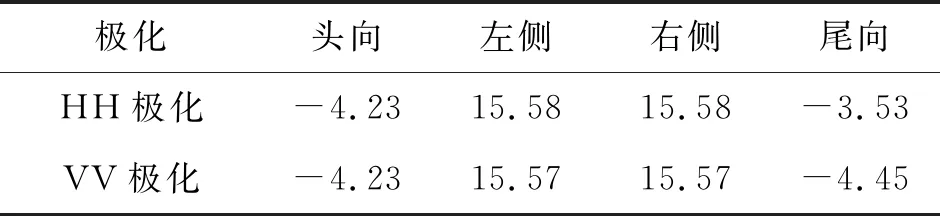
表5 机身+常规桨毂主要角域RCS(单位:dBsm)

对比单独无人机机身与“机身+常规桨毂”组合体的RCS曲线与主要角域RCS均值可见:常规桨毂在头向与尾向附近产生了明显的散射增强,组合体在该方向的RCS均值大幅超出了单独机身,增加近15 dBsm,相比单独机身的RCS增长量级基本对应于常规桨毂的RCS水平。而在侧向,桨毂产生的RCS增加基本淹没在机身侧面的强烈镜面散射中。

由以上仿真计算与分析可得,若想控制无人直升机的雷达散射水平,尤其是主要威胁角域的头向RCS,必须对桨毂进行RCS缩减设计。

4 桨毂RCS缩减优化设计分析

由于常规桨毂自身复杂的布局结构与功能需求,难以直接对其进行外形与结构更改,因此本文选择在常规桨毂外侧增加桨毂遮罩的形式来进行RCS缩减优化。

依据常规桨毂的外形结构,采用双圆台造型设计桨毂遮罩,顶部与底部半径250 mm,中间半径420 mm,相对常规桨毂外形如图10;保持遮罩总高度H不变,以中间圆相对底面高度h为变量,以20 mm为步长从50 mm到170 mm,设计了一系列桨毂遮罩,如图11与表6。

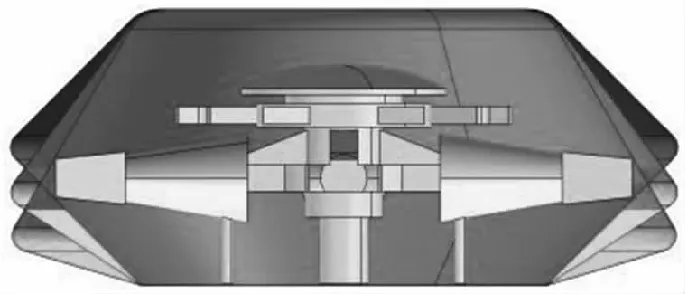
图10 桨毂遮罩纵剖面示意图

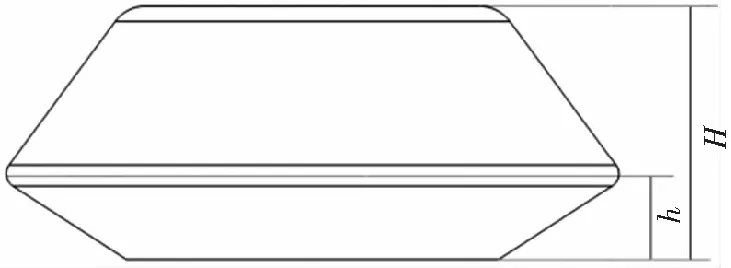
图11 桨毂遮罩几何轮廓

表6 桨毂遮罩高度参数

采用本文方法求解桨毂遮罩在水平入射的6 GHz平面波HH极化与VV极化下的RCS。由于在该条件下桨毂遮罩外形具有各向同性,因此随入射角方位变化的雷达散射特性基本一致。表7给出了各桨毂遮罩在两种极化下的RCS均值。桨毂遮罩系列RCS对比如图12。

表7 桨毂遮罩RCS均值(单位:dBsm)

图12 桨毂遮罩RCS对比

由此可见,对于单独的桨毂遮罩,中间圆高度h对HH与VV极化RCS的影响极小。这是由于总高度H不变时,中间圆高度h的变化引起的上下圆台锥体角变化是线性关联的,桨毂遮罩整体外形截面积基本不变,因此雷达散射特性基本一致。对比常规桨毂头向±30°RCS均值,可见本文设计的桨毂遮罩系列对于RCS缩减控制具有明显作用,缩减10 dBsm以上。

进一步将无人机机身与各桨毂遮罩组合,如图13,依次计算组合体在水平入射的6 GHz平面波HH极化与VV极化下的RCS,得到主要威胁角域头向±30°的RCS均值,见表8。

图13 机身+桨毂遮罩组合体网格划分

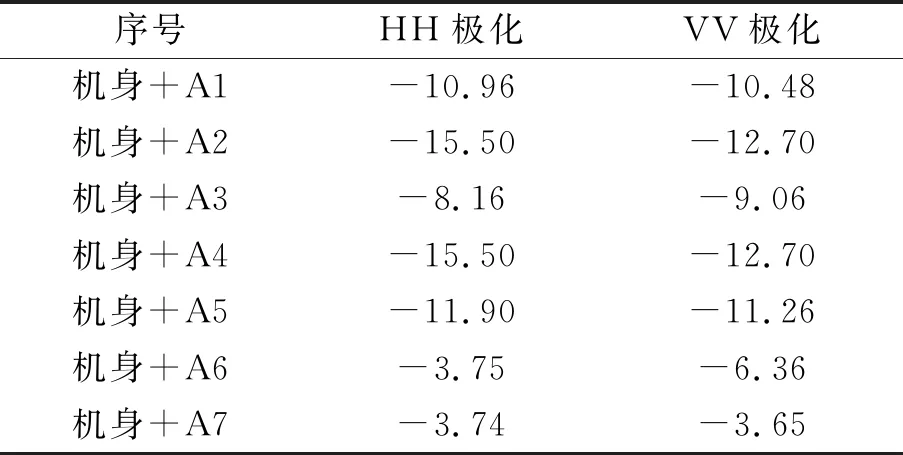
表8 组合体头向±30°RCS均值(单位:dBsm)

由“机身+桨毂遮罩”系列组合体与“机身+常规桨毂”组合体头向±30°RCS均值对比(图14)可见,遮罩方案A1、A2、A3、A4、A5对组合体RCS均有不同程度的缩减,其中A2、A4效果最佳,缩减达10 dBsm以上;但A6与A7方案效果较差甚至出现扩大。

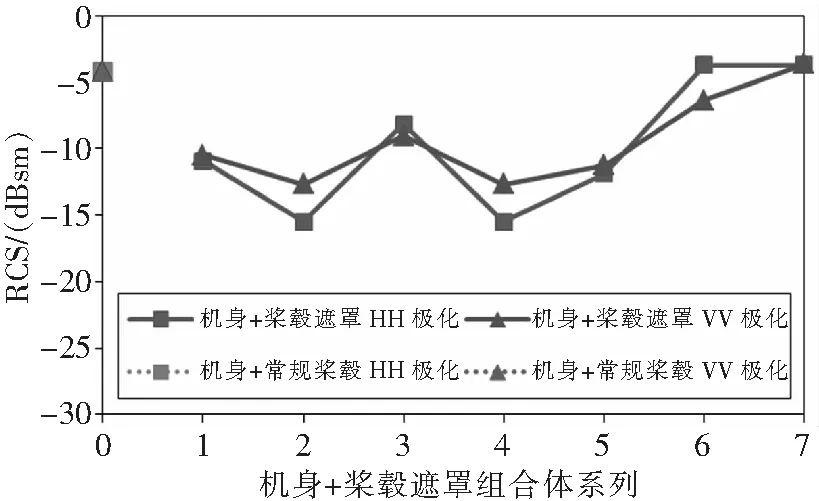
图14 机身+桨毂遮罩组合体RCS对比

分析主要影响因素在于桨毂遮罩下圆台与机身上表面形成的角反射器。随着桨毂遮罩中间圆高度h的变化,角反射器的夹角也在变化。对于A1-A5方案,角反射器夹角较小,入射波经多次反射与散射后不断衰减和偏转,因此产生的后向雷达散射相对较小。其中,A3方案角反射器夹角约28°,入射波经多次反射后回波主瓣靠近入射波反向,因此相比于A1、A2、A4与A5方案RCS有所增加,但仍低于“机身+常规桨毂”组合体。

A7方案角反射器夹角为45°,入射波经3次镜面反射后原路返回,因此产生了强烈的回波散射。A6方案夹角略小于A7,经4次反射回波主瓣也靠近入射波反向,会产生较强的回波散射。

5 结论

本文采用RLGO仿真算法,对典型散射源角反射器算例进行了仿真计算,同已有的经典数据进行了对比验证;通过对无人机机身与常规桨毂RCS的独立与组合计算,分析了水平入射波下机身与桨毂的散射特性,以及桨毂对无人直升机RCS的影响;设计了一系列桨毂遮罩以优化缩减雷达散射,仿真计算了各桨毂遮罩及其与机身组合体的RCS,并对散射特性进行了对比分析。获得了以下主要结论:

1)本文采用的RLGO方法,可以有效且快速计算包括多次反射与绕射的直升机与桨毂雷达散射特性。

2)常规桨毂由于外形结构复杂,具有较强的雷达散射特性和明显的周期性,其RCS甚至超过机身外形本身,造成无人直升机头向雷达散射均值增大近15 dBsm。

3)采用桨毂遮罩的形式可以有效缩减常规桨毂带来的强散射。缩减效果较好的方案,无人直升机头向RCS均值缩减达10 dBsm以上。不同几何参数的遮罩外形会与机身形成不同的角反射器,在RCS方案设计中需要精细化设计和针对性分析评估。