基于有限元的边坡稳定可靠度改进一次二阶矩法研究

汪安南，林潮宁，李同春，2，齐慧君，邵天成

(1.河海大学水利水电学院，江苏 南京 210024；2.水安全与水科学协同创新中心，江苏 南京 210024)

1 研究背景

边坡失稳引起的滑坡灾害已成为全球范围内主要地质灾害之一[1]。由大型边坡失稳和滑坡引起的工程事故历史上屡见不鲜[2]，且其造成的后果也是不可估计的，因此边坡的抗滑稳定安全度研究成为国内外工程界十分关心的研究课题[3]。目前，在边坡稳定性分析方面的研究大致可以分为2类：一类是由极限平衡法和数值计算方法所组成的确定性分析方法[4]；另一类是考虑参数随机性、变异性的可靠性分析方法[5]。相比于确定性分析，可靠性分析方法考虑了参数不确定性对边坡稳定性的影响，更接近实际情况。

常用的边坡可靠性分析方法主要有蒙特卡洛法、响应面法及一次二阶矩法等。李育超等[6]将蒙特卡洛法与有限元法相结合，利用随机走步法不断更新试算滑动面，确定了边坡临界滑动面及其对应的最小安全系数；何淑军等[7]采用蒙特卡洛法对夏呀河四级滑坡进行可靠性分析，定量地表达了该滑坡的安全程度；周罕等[8]采用响应面法和强度折减法相结合的分析方法，把安全系数和破坏概率作为综合评价边坡稳定性的指标，从不同角度对边坡可靠性进行分析；陈昌富等[9]基于响应面法建立了一种高效的边坡可靠指标和失效概率近似计算方法，大大降低了构造响应面函数的计算工作量；朱彦鹏等[10]基于改进一次二阶矩法建立了锚定板挡土墙的系统可靠度分析模型，分析了参数在不同变异系数下对系统可靠度指标的影响和土性参数敏感性。通常，当功能函数为隐式时，仅蒙特卡洛法和响应面法可用，但蒙特卡洛法的模拟次数多，计算效率低；响应面法通过不同的响应面函数重构隐式功能函数，但采用传统响应面形式处理复杂问题计算精度有限，采用机器学习算法构建响应面函数涉及超参数选取等问题，计算复杂度高[11]。

考虑上述方法在处理边坡隐式极限状态函数时的问题，本文提出一种基于有限元的边坡稳定可靠度改进一次二阶矩法，定义极限状态函数为滑体极限状态下抗滑力与下滑力的差值，考虑黏聚力及内摩擦角作为随机变量并且服从独立正态分布，求出极限状态方程中随机变量的偏导数，基于改进一次二阶矩法编写了求解边坡失稳概率和可靠指标的计算程序，通过算例验证了所提方法的适用性，并对某库岸边坡进行了可靠性分析。

2 显式极限状态函数的建立及改进一次二阶矩法原理

2.1 边坡显式极限状态函数

有限元迭代解法[3]是一种以刚体极限平衡基本思想为基础的直接迭代解法，是一种在滑动面已知情况下边坡稳定分析的有效方法，不仅可计算出边坡沿已知滑动面的安全系数，且能同时给出边坡临界失稳时的位移场与应力场。

用有限元迭代解法分析时，边坡稳定的非线性特性主要反映在滑动面上，滑动面上的强度准则一般采用摩尔-库伦准则。滑动面的单元形式主要采用文献[12]中提出的常规的矩形(平面)或立方体(空间)的统一模式。当边坡处于临界稳定状态时，滑动面上的滑动力和阻滑力满足

(1)

式中，m为危岩体内滑动面单元个数；Wi为第i个滑动面单元上的法向力；Pi为第i个滑动面单元上的切向力；Ai为第i个滑动面单元上扣除受拉区后的面积；ci为第i个滑动面单元上的黏聚力；φi为第i个滑动面单元上的内摩擦角；K为假定安全系数；K*为真实的抗滑稳定安全系数。

由于力的矢量特征，安全系数为在边坡潜在滑动面上总抗滑力矢在整体下滑趋势方向上投影的代数和与总下滑力矢在此方向上投影代数和的比值。当滑体处于极限平衡状态时，安全系数即为极限抗滑力与下滑力的代数和比值。将边坡滑动面上的滑动力达到抗滑力作为边坡极限状态的标志，故将抗力函数R和作用函数S相等的情况作为极限状态，即

(2)

式中，S(g)为作用函数；R(g)为抗力函数；g为函数变量；Z0为功能函数。对随机变量求偏导数得

(3)

式中，Z为功能函数；fi为第i个滑动面单元上的内摩擦系数；X为随机变量的向量表示，X1i、X2i分别为X的第1个、第2个随机变量。

2.2 改进一次二阶矩法的基本原理及计算步骤

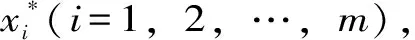
(4)

(5)

根据随机变量线性组合的性质及可靠指标的定义，可得

(6)

对式(3)、(4)进行变换，得设计验算点在原始X空间中的坐标为

xi=μXi+βσXicosθXi

(7)

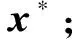
3 算例验证

3.1 计算模型

含有1个确定性滑面的边坡算例是边坡稳定分析中非常经典的例子[13]，其二维模型结构清晰，受力状态简单，可以得到其力学上的解析解。单一接触面岩质滑坡体几何尺寸见图1。岩土体抗剪强度参数视为随机变量，服从正态分布，具体数值见表1。

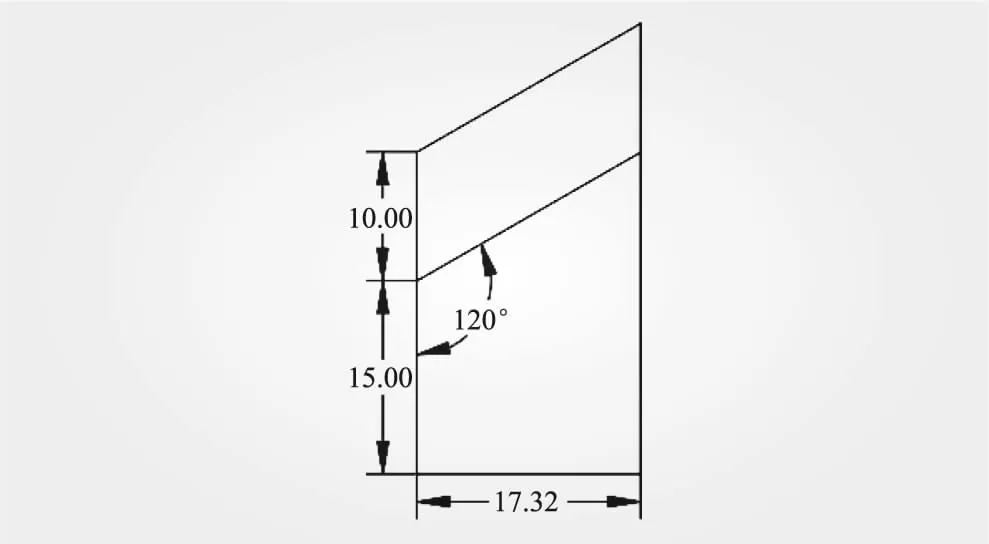
图1 单一接触面岩质滑坡体截面(单位：m)

表1 岩土体物理力学参数

相关研究显示，变量之间的相关性对可靠指标的影响较小，可以认为是相互独立的[14-15]，暂不考虑黏聚力与内摩擦角的相关性。目前研究中[16-17]，对于岩土体黏聚力及内摩擦角变异系数的取值均在0.1～0.3范围内，本算例岩质材料的黏聚力及内摩擦角的变异系数取值为0.15。边坡显式极限状态函数中滑动面上各单元的切向力及法向力采用非线性有限元方法求取，综合考虑时间和计算精度，建立有限元计算模型，见图2。共560个单元，609个节点。底部基岩的两侧和底部边界均为固定约束，上部滑动块体为自由边界。

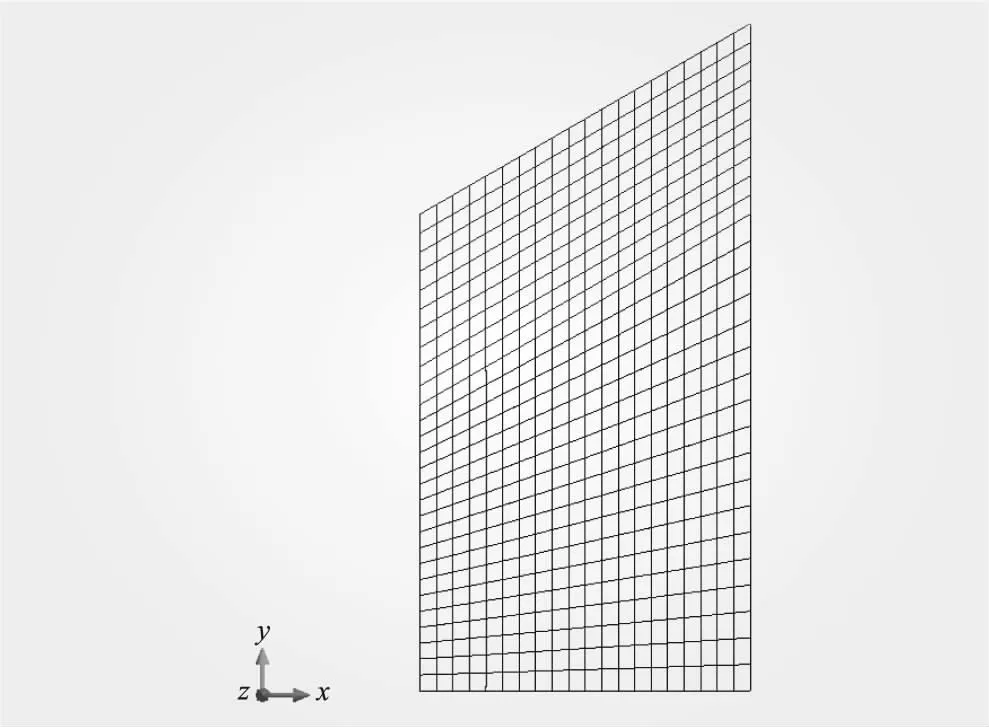
图2 有限元计算模型

3.2 计算过程与分析

荷载考虑边坡自身重力，采用非线性有限元计算滑动面上单元切向力、法向力，建立边坡滑动面的显式极限状态函数；依据验算点法的边坡可靠性分析流程，进行可靠指标的迭代计算。按照本文的边坡可靠指标计算流程，共进行2轮可靠指标的迭代计算即满足精度要求，所以该边坡的可靠指标为1.493 9，其破坏概率为6.76%。

通常，蒙特卡洛法计算结果可作为基准解[18]。为验证本文所提方法计算结果的准确性，结合蒙特卡洛法与有限元强度折减法，经过100 000次的蒙特卡洛模拟，得到该边坡的失效概率为6.18%，计算耗时约为6.0×105s(166.67 h)，总抗滑力投影与下滑力投影差值分布见图3。从图3可知，本文方法计算结果与蒙特卡洛法计算结果相比，误差在3%以内，说明本文方法计算出来的失效概率与蒙特卡洛法的计算结果具有可比性，计算结果合理可行。

图3 边坡总抗滑力投影与下滑力投影差值分布

同时，采用其他目前常用的可靠性分析方法对该边坡算例进行计算，结果见表2。基于本文建立的显式极限状态函数，采用均值一次二阶矩法对该边坡算例进行可靠性分析，失效概率为12.04%，此结果与蒙特卡洛法计算结果相比，误差为94.82%。采用基于二次多项式响应面函数的改进一次二阶矩法对该边坡算例进行可靠性分析，失效概率为5.21%，此结果与蒙特卡洛法计算结果相比，误差为15.70%。说明本文所提方法相比于均值一次二阶矩法、响应面法具有更高的计算精度。此外，相比于响应面法的较高计算复杂度，本文方法计算过程简单易于操作，能考虑滑坡体、岩基力学特性的不均匀性及滑动面上的应力分布影响。

表2 可靠性计算结果

4 工程应用

4.1 工程概况

某库岸边坡位于右岸坝前，距大坝900～1 700 m，坡高650～700 m，为花岗岩岩质边坡，陡倾岸内及岸外构造发育。根据地质勘探结果，该库岸岩体分为散体结构、碎裂结构、块裂结构和镶嵌一次块状结构4种。其中，散体结构水平厚度一般小于30 m，碎裂结构一般在40～60 m，块裂结构一般在50～80 m。此外，岸坡平台还分布几条拉裂陷落带，其中规模较大的有LF54和LF55等。3号梁库岸岩体结构见图4。

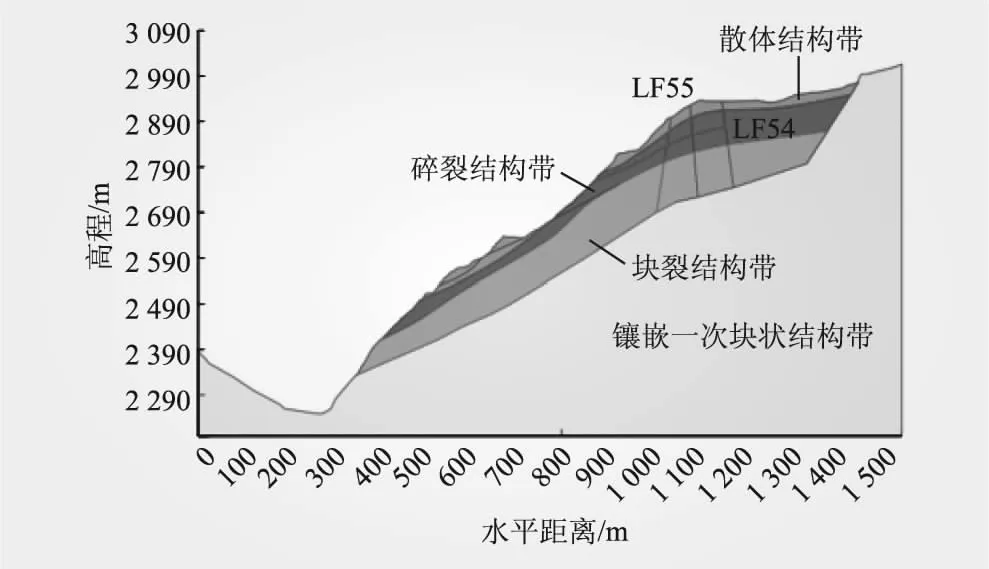
图4 库岸岩体结构

4.2 计算模型

本文选取3号梁地质剖面，底部全长1.582 km，高差0.788 km。在此基础上，建立了1组整体稳定分析模型和3组局部稳定性分析模型，见图5、6。为考虑该变形体是否存在整体失稳的可能，对库岸沿变形和非变形界限的抗滑稳定性进行分析，选取了3号梁地质剖面，以地质勘查推测的变形范围界限和碎裂岩体下限为假定滑动面。对于局部稳定分析，指定滑动面以顶部平台出露的LF54为后缘拉开面，以岩体结构面为假定滑面，以不同埋深深度分别进行分析，局部计算模型见图6。

图5 整体稳定计算模型

图6 局部稳定计算模型

由于本文给出的极限状态函数含有边坡滑动面各单元的切向力及法向力，采用非线性有限元法计算，根据工程地质剖面图，建立相应的数值模型，见图7。综合考虑计算时间和精度，有限元计算模型共1 616个单元，1 736个节点；边界条件为下部固定，左右两侧水平约束，上部为自由边界。

图7 稳定性分析模型

覆盖层除外，计算模型岩体参数取值见表3。考虑滑动面抗剪强度参数指标c、f为随机变量进行可靠度分析，结合同类岩土工程经验，可以认为各滑动面强度参数服从正态分布，统计特性指标见表4。由于边坡上建筑物荷载条件未明确，故未考虑坡体加载的影响。

表3 岩体力学参数取值

表4 结构面参数统计特征值

4.3 计算过程与分析

采用非线性有限元法计算滑动面单元的切向力和法向力，建立滑动面的显式极限状态函数；依据验算点法的边坡可靠度分析流程，对整体及局部共4种假定滑动面进行可靠指标的迭代计算，直到满足精度为止；为对边坡的安全状态有更全面的认识，采用岩体及各滑动面强度参数的平均值作为标准值，采用有限元强度折减法进行安全系数计算，计算结果见表5。

从表5可知，整体及局部的安全系数均高于现行边坡规范抗滑稳定安全系数控制下限值1.15，然而局部的失稳概率较高，需适当的采取工程措施以降低风险。该计算结果与实际监测中边坡局部出现拉裂、位错及坡面坍塌等变形破坏但整体保持稳定的现象互相印证。安全系数与可靠性分析对边坡局部状态判断出现矛盾的原因是：①表征边坡稳定性的安全系数没有考虑材料参数的变异性，低估了边坡局部的失稳风险；②散体结构带和碎裂结构带浅表部材料参数虽然均值较高，但是变异性大(滑动面岩土体的变异系数都达到0.3)，导致边坡局部失稳概率较大。

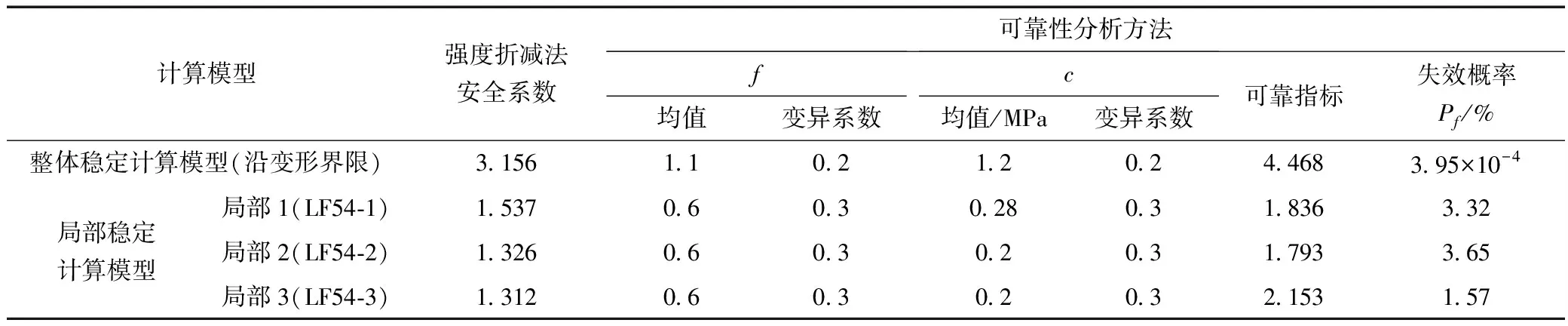
表5 各计算模型可靠指标计算结果

因此，应采取分级放坡[8]，加强对边坡的支护处理。为保持边坡的长久稳定，应植草对坡面进行防冲刷处理，对外露的坡面采用格构式等形式进行护坡。在做好坡上截水、坡体排水、坡面防护等综合治理的同时，应加强对边坡的监测及数据分析，做好灾害的主动防范，提前预报。

5 结 语

针对蒙特卡洛法与响应面法在处理边坡隐式极限状态函数时的问题，本文提出了一种基于有限元的边坡稳定可靠度改进一次二阶矩法，建立了边坡显式极限状态函数，并应用于某库岸边坡可靠性分析中，得出以下结论：

(1)与已有的可靠性分析不同，本文定义极限状态函数为滑体极限状态下抗滑力与下滑力的差值，考虑黏聚力及内摩擦角作为随机变量并且服从独立正态分布，求出极限状态方程中随机变量的偏导数，在降低计算复杂度，提升计算效率的同时保证计算精度，计算精度上优于响应面法，计算效率上优于蒙特卡洛法。

(2)采用本文提出的边坡可靠度分析方法，多角度综合分析了某库岸边坡的稳定性。由于滑坡稳定性分析不可能考虑全部的影响因素，因此除了岩土体的抗剪强度参数黏聚力、内摩擦角外，考虑其他参数影响的边坡可靠性分析需要进一步研究。