土壤原位触探技术与贯入机理研究进展
2023-04-10刘晴昊李玉琼崔高瞻
刘晴昊,李玉琼,李 娜,薛 健,崔高瞻,邹 欧
(1.中国科学院大学 工程科学学院,北京 100049;2.中国科学院 力学研究所 流固耦合系统力学重点实验室,北京 100190;3.中国科学院 力学研究所 非线性力学国家重点实验室,北京 100190)
1 引言
准确、快速地获取土壤介质的物理力学参数,在海洋岩土勘探、行星科考与载人登陆、军用车辆越野路面机动性评估等民用与国防领域有重大科学与工程需求。然而,土壤介质由于其多相性、散粒性等特点,具有复杂的物理力学特性,这为准确获取土壤介质的物理力学参数带来了巨大的挑战。
目前,获取土壤物理力学参数的技术主要包括3 类:物理勘探、室内试验和原位触探。其中,物理勘探的技术手段主要包括车载与机载探地雷达、高光谱卫星等。该技术采用高光谱遥感法、伽马射线能量谱法等方法,并借助神经网络算法、模式识别及关联匹配算法,实现远程广域地面土壤物质属性的反演和评估。但物理勘探属于非接触测量,受分辨率及复杂环境因素扰动等影响,不能准确反演地面土壤的力学特性,仅能得到土壤的类型及大致的属性。室内试验技术手段主要包括直剪试验、侧限压缩试验、三轴试验等,能够较准确地测量土壤强度及变形特性。但室内试验需要对目标土壤取样,在目标土壤取样困难的应用场景下无法满足测量需求,而且取样和运输过程中会造成土体原有结构的扰动与含水量损失,导致室内试验难以获得原状土的物理力学特性参数。原位触探技术通过将探头贯入土体中,根据探头传感器测量的数据,实现密度、强度和模量等土壤物理力学参数的解译。以上分析表明,土壤原位触探技术弥补了前两种技术的不足,同时具有可连续测试的优点,因此在工程领域中得到广泛应用。
原位触探技术可准确获取土壤的分层、地基承载力和地震液化等工程特性参数,为房屋、公路、隧道、桥梁等水陆基础设施建设,以及港口与海上石油钻井平台的锚泊系统、海底管道等海洋设施建设提供重要的数据支撑[1-4]。此外,利用原位触探技术开展行星地质勘探,比钻探取样、室内试验的手段更加经济。它能在复杂的重力、气压、温度和辐射等环境条件下获取星壤的原位力学特性,为行星科考、科研站与基地建设和资源开发等任务提供重要支撑[5]。原位触探技术可快速并准确获取广域地面的承压、剪切等物理力学特性,从而预测行驶车辆的车轮沉陷量、阻力和牵引力等指标,并进而实现军用车辆在越野路面的机动性评估[6-7]。
利用原位触探技术获取土壤的物理力学参数需要厘清贯入过程中探头与土体的相互作用机理,在此基础上,建立贯入阻力与土壤物理力学参数的函数关系并进行解译。相关学者围绕原位触探的贯入机理,在理论分析、数值模拟和试验这3 方面开展了大量的研究,但探头贯入的整个过程涉及土体的动态响应、大变形和非线性本构等复杂问题,这为唯象模型的建立带来了困难[8];而试验方法主要以室内模型槽试验为主,仍存在边界效应和尺寸效应等问题。因此,仍需对土壤原位触探技术与贯入机理进行完善和系统性总结。
本文第2 章介绍了土壤原位触探技术的发展进程、主要的仪器构成、基本原理和工程应用;第3 章针对两种典型的土壤原位触探技术总结了相应的贯入机理研究方法及研究现状;第4 章对目前的土壤原位触探技术及贯入机理研究进行了总结展望。
2 土壤原位触探技术
围绕工程领域的应用需求,国内外在土壤原位触探技术上不断改进与创新,涌现了各类原位触探设备与技术方法。如图1 所示,本章根据探头贯入土体方式的不同,将其分为静力触探和动力触探两大类进行系统介绍。其中静力触探的探头是以20 mm/s 的速度匀速贯入[9],可视为准静态过程。动力触探的探头在土体阻力作用下作减速贯入,是动态过程。
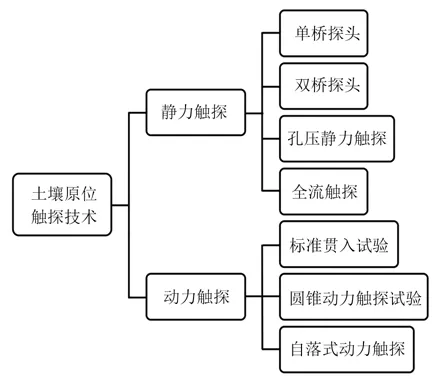
图1 土壤原位触探技术分类Fig.1 Classification of soilin-situpenetration technology
2.1 静力触探
2.1.1 国内外静力触探技术发展概述
静力触探(Cone Penetration Test,CPT)的基本原理是对装有传感器的金属探头进行准静态加载,使其以20 mm/s 的速度(ISO 标准[9])贯入土中,通过传感器测得锥尖阻力、侧壁摩擦阻力等数据,然后基于探头与土体相互作用的机理,反演土壤物理力学参数。
CPT 技术最早源自荷兰。1932 年,荷兰工程师Barentsen[10]最先开展圆锥静力触探试验,可用人工加载的方式将探头贯入土体12 m 深,并通过压力计读取贯入阻力,其探头荷兰锥尺寸如图2 所示。1935 年,荷兰Delft 土力学实验室(DSML)设计了一款采用1×104kg 重探杆的人工圆锥静力触探仪[1]。1948 年,DSML 改进了圆锥探头并开发出电测式探头[11-12],相比于原来的机械式探头,其可实现连续贯入和实时读数,并且对贯入阻力等数据的测量更加准确。

图2 荷兰锥尺寸[11]Fig.2 Size of Dutch cone[11]
1953 年,Begemann[13]在机械式圆锥探头 上添加摩擦套筒,使探头能同时测量锥尖阻力和侧壁摩擦阻力。在此基础上,荷兰Fugro 公司于1965 年研制出摩擦电测探头[14],消除了机械式摩擦探头由于内钻杆与外管套摩擦带来的误差,该探头被国际土力学和基础工程学会(ISSMFE)作为标准[15]采用,如图3 所示[16]。
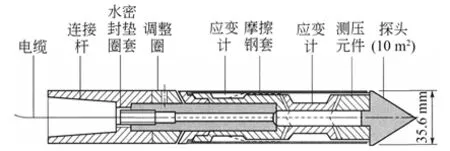
图3 Fugro 摩擦电测探头[16]Fig.3 Fugro electric friction cone[16]
1975 年,Wissa 等[17]、Torstensson 等[18]研 制出电测式孔隙水压探头。1980 年后,在CPT 的基础上,出现了可测量孔隙水压的孔压静力触探技术(Piezocone Penetration Test,CPTU),CPTU 能得到经孔压修正后的有效贯入阻力,被广泛应用于软黏土的原位测试。1980 年以来,CPTU 技术与多种新型的传感器相结合,朝着土体物理力学参数解译的多功能化、集成化和数字化方向发展[3],如图4 为两种目前应用广泛的新型传感器。

图4 两种与CPTU 结合的新型传感器Fig.4 Two new sensors combined with CPTU
上世纪90 年代,Stewart 等[19]基于全流理论提出全流触探仪,并研制了T 型、球型和碟形探头,解决了CPTU 在海底超软土原位测试中精度不高的问题。
国内的静力触探技术起步较晚,1954 年从荷兰引进机械式单桥CPT[20]。1964 年,王钟琦[21]研制了国内第一台电测式单桥CPT。20 世纪70年代,国内研制出能同时测量锥尖阻力和侧壁阻力的双桥探头。20 世纪90 年代,国内开始引进CPTU 技术进行相关研究,并在工程中初步应用[24-25]。同一时期,南京水利科学院、浙江南光地质仪器厂等单位仿制了CPTU 探头。近年来,蔡国军等[26-27]提出了适用于国内规范的CPTU 解释方法,对CPTU 在国内的推广应用做出了贡献。东南大学结合现代数字传感技术、嵌入式系统和计算技术,成功研制新一代多功能CPTU 测试系统,且自主研发了全流触探T 型和球型探头[28-29]。
综上,静力触探技术在测试手段方面,经历了机械式探测、电学式探测、电子式探测和数字式探测4 个阶段。在探头的数据测量功能方面,由最初的只能测量总贯入阻力的单桥探头,发展为能同时测量锥尖阻力和侧壁摩擦阻力的双桥探头,并在此基础上研制出能测量孔隙水压的CPTU 和测量海底超软土不排水抗剪强度的全流触探仪。目前,CPTU 探头在与新型传感器结合后,其数据测量功能更加多样化。
2.1.2 静力触探试验仪器组成与原理
静力触探试验系统主要由加压系统、数据传输系统和探头3 部分组成。
(1)加压系统
加压系统通过施加外载荷维持探头的匀速垂直贯入。在不同的测量环境下,加压系统存在差异,静力触探设备的加压系统如图5 所示。小型静力触探仪可利用人的自重以双手按压的方式下进行加压,也可以使用手摇式加压系统,如图5(a)所示。早期的CPT 一般采用该加压方式,但其提供的外载荷较小,只能满足较简单的测量需求。现代CPT 技术的大型加压系统通常能提供100~200 kN 的压力,在陆上静力触探试验中通常使用卡车式或履带车式加压系统(分别如图5(b)和图5(c)),在水上静力触探试验中使用自升式(如图5(d))、套管式、海床式、下孔式、潜水舱式加压系统,能够满足绝大部分应用场景下的测量需求。

图5 静力触探设备的加压系统Fig.5 Pressurization system for cone penetration test
海床式和下孔式加压系统主要应用在水深大于40 m 的深海静力触探试验,如图6 所示。海床式通过轮驱动产生持续推力将探头连续地贯入海底土层;下孔式先通过钻杆在土层钻孔,后将探头贯入钻孔下的土层,如此循环往复操作。下孔式的贯入深度远大于海床式,可穿过硬土层,但由于它是周期性贯入,得不到连续的土层剖面贯入数据,且钻孔过程会对测试土层造成扰动。目前,国内外研制了多款先进的深海静力触探测试系统,具体如表1 所示。
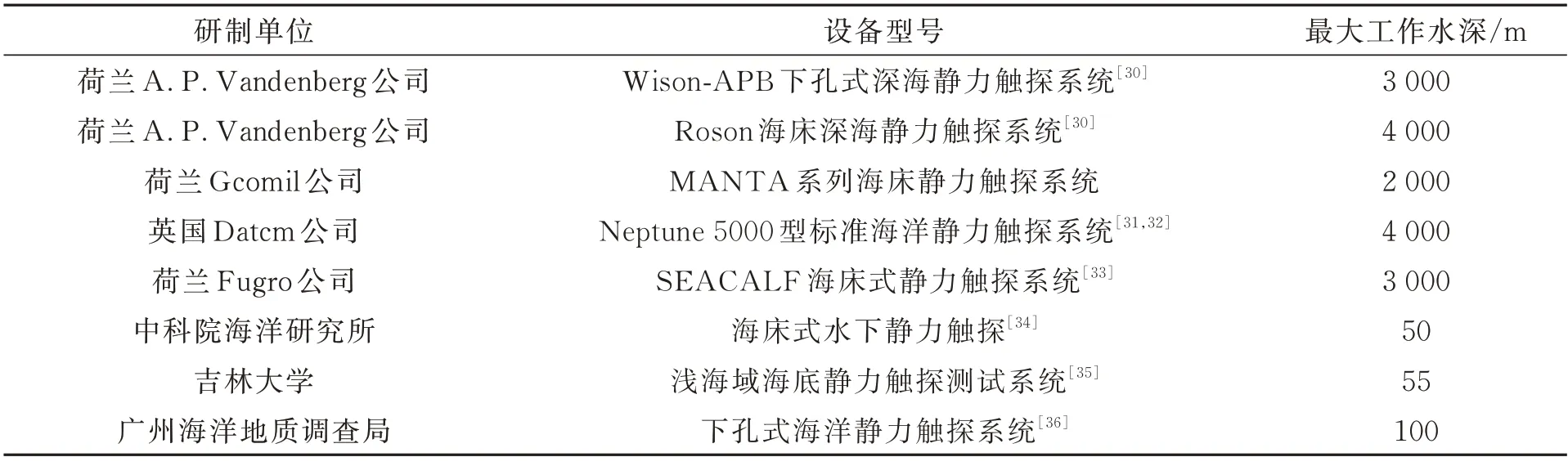
表1 国内外部分深海静力触探测试系统Tab.1 Some deep-sea cone penetration test systems in China and abroad

图6 两种深海静力触探设备的加压系统Fig.6 Two modes of pressurization system for cone penetration test in offshore
(2)数据传输系统
在静力触探测试过程中,传感器的实时测试信号在探头内部进行转换后,需通过数据传输系统到达地面的计算机进行处理。目前的数据传输方式主要有电缆式传输、无线传输和存储模块存放。其中电缆传输方式比较普遍,但在深海静力触探中,电缆线显得冗杂;而通过存储模块存放无法即时传输数据,也就无法实现土壤参数的快速解译。上世纪90 年代前后,俄罗斯、日本、瑞典和美国等研制出无线传输系统,探头测试数据以无线电波或声波的方式实时传输至地面,解决了上述问题。在国内,东南大学联合南光地质仪器有限公司也研发了使用无线电传输系统的NCT-1 型静力触探仪[2],如图7 所示。

图7 NCT-1 型无线静力触探系统[2]Fig.7 NCT-1 wireless cone penetration test system[2]
(3)探头
静力触探试验根据探头类型可分为单桥CPT、双桥CPT、CPTU、全流触探试验等。单桥CPT 只能测量贯入土体过程的总阻力Q,除以锥底面积A可得到总比贯入阻力ps。双桥CPT 能分别测量锥尖阻力qc和侧壁阻力fs,如式(1)(2)所示:
其中:Qc为锥尖的总阻力,Qs为侧壁的总摩擦阻力,As为侧壁摩擦套筒的表面积。
CPTU 是在双桥CPT 的基础上加装了孔压传感器,以测量锥尖处的孔隙水压力,进而能对锥尖阻力进行孔压修正(式(3))及土体上覆应力修正(式(4)),得到有效锥尖阻力qnet。
其中:qc为实测锥尖阻力;qt为孔隙水压力修正后的净锥尖阻力;u2为锥肩处孔隙水压力;σv0为土体上覆应力,即土的重度与贯入深度的乘积γh;α为有效面积比[15]。此外,孔压传感器在贯入停止后继续采集数据,可进行孔压消散试验,评估土壤的固结特性。
荷兰Fugro 公司和A.P.Vandenberg 公司,英国的海洋科学研究所、Datem 公司和Lankelma公司,美国Minnesota 公司和ConeTech 公司等,针对不同应用需求研制了多种新型传感器,直接安装在CPTU 上,使其实现多功能化和集成化[3,37-38]。表2 列出了一些国际上已研制成功的CPTU 新型传感器[1,16,39]。

表2 CPTU 新型传感器Tab.2 New sensors combined with CPTU
目前,全流触探仪的探头类型有T 型、球型和碟形[57-59],如图8(a)所示。根据国际通用的挪威NORSOK G-001 规范[60]规定,标准T 型探头尺寸为直径40 mm、长250 mm、投影面积10 000 mm2。球型探头尺寸尚未有明确标准,Randolph[61]建议球型探头直径为115 mm、投影面积为10 000 mm2,并直接与标准探杆连接。全流触探仪的探测原理基于全流理论,贯入过程中呈黏性流体状态的海底超软土在探头附近流动,如图8(b),通过分析两者之间的摩擦可获得超软土的不排水抗剪强度,相比于CPTU 的解译更精准。这是因为全流触探的贯入阻力受孔压和上覆应力影响较小,其修正公式为:
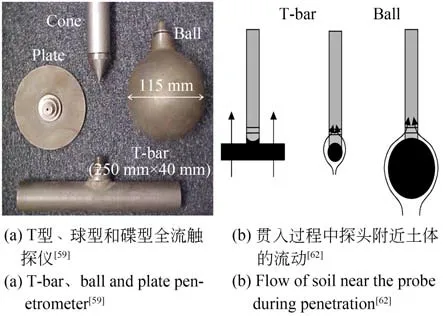
图8 全流触探仪Fig.8 Full-flow penetrometer
其中:qm为实测贯入阻力,As和Ap分别为探杆和探头在垂直于贯入方向上的截面面积。对于全流触探仪的As/Ap一般小于1/10,因此孔压和上覆应力的影响较小。
综上,静力触探加压系统提供探头匀速贯入所需的动力,人工加压系统便捷但贯入深度浅,而大型加压系统解决了贯入深度的问题,但体积和质量均较大。在海洋静力触探中,大型静力触探试验系统需要大型船只作为运载平台并配备有大型起重机或绞车,导致其操作复杂、综合成本较高、耗时较长、同时极易受天气影响[63]。在静力触探数据传输系统方面,目前电缆式传输应用较多,但无线传输是未来的发展趋势。静力触探探头的发展趋势是与多种新型传感器结合,以满足更多具体应用场景的探测需求,实现探头传感器数据采集的数字化,探头功能的集成化,使探头结构更加轻巧紧凑。
2.1.3 静力触探技术的工程应用
静力触探技术在传统的陆地与海洋岩土工程勘探领域已经比较成熟并实现了产品化,占据部分发达国家土体勘察量的70%以上,成为与地质钻探取样、室内试验相辅相成且互为借鉴的重要岩土勘察手段,并在许多国家被列入国家规范。其具体工程应用包括确定土体分层、土质分类,桩基础的承载力评估、沉降计算,土壤抗液化分析,确定土的应力历史与初始应力状态,评估土壤的强度特性、变形特性、固结与渗流特性,探测土层污染物等。刘松玉等[16]总结了国内外针对上述方面的应用情况。
静力触探技术还被应用在行星表面力学特性探测领域。NASA 在阿波罗14 号任务中使用了铝制的圆锥透度计(Cone Penetrometer)。宇航员通过双手按压的方式将直径9.5 mm、锥角30°的圆锥透度计压入月壤中,并从测力环上的千分表读取贯入阻力,从探杆上的环形标线读取贯入深度,最后得到贯入阻力与深度的变化关系,如图9(a)[64]。NASA 在阿波罗15 和16 号任务中采用SRP 贯入仪(Self Recording Penetrometer)进行月壤原位测试。SRP 贯入仪末端为圆锥与平板,由宇航员施加外力推入月壤中,连续的贯入阻力-深度曲线将由划线器自动记录在贯入仪上端的金属圆筒上,如图9(b)[65]。前苏联在月球13 号任务的着陆器上搭载了圆锥贯入装置。该装置的圆锥探头高13 mm,直径35 mm,锥角103°,贯入月壤的动力由一台小型燃料发动机提供,如图9(c)[66]。前苏联在月球17 和21 号任务的Lunokhod 月球车上搭载了Cone-vane 贯入仪测量月壤的承压与剪切强度。Cone-vane 贯入仪的探头由圆锥和两片对称的垂直叶片组成,圆锥直径50 mm,锥角60°,叶片宽70 mm,高44 mm,如图9(d)所示[67]。前苏联在金星13 和14 号任务中使用圆锥装置成功测试了着陆点的地面力学特性[68]。

图9 行星探测任务中使用的静力触探设备Fig.9 Cone penetration test used in planetary exploration mission
阿波罗14 号任务进行了3 次贯入试验[69],在70~135 N 的贯入阻力下,贯入深度分别是42 cm、44 cm 和50 cm。阿波罗15 与16 号任务共进行了17 次贯入实验[70],贯入深度最大为74 cm,且仅有8 次实验贯入深度超过20 cm。这是因为圆锥透度计与SRP 贯入仪通过宇航员双手按压的方式贯入,提供的压力仅约为200 N,使得贯入深度很浅。前苏联月球13 号任务的贯入深度约4.5 cm[66],月 球17 号和21 号共进行了千余次 贯入试验,贯入深度均不足10 cm[67],仅能测量表层月壤的力学特性,无法满足进一步的行星地质勘探要求。受目前火箭运载能力的限制,可提供足够贯入深度的大型静力触探设备短期内无法大规模应用于行星探测工程。
静力触探技术凭借其便捷的优势、能够获得大区域范围内地面力学特性、可评估该区域的越野通过性、甚至能满足绘制区域车辆通过性云图的军事需求,故被广泛应用于车辆地面力学领域中的军用装备通过性评估。1947 年,美国陆军工程师研究和发展中心(ERDC)提出基于圆锥指数CI评估车辆支撑通过性的圆锥指数法。其中,圆锥指数CI可通过圆锥透度计测得,为贯入阻力与圆锥横截面积的比值。圆锥指数法选择多种有代表性的车辆在相关地面进行通过性测试,建立基于车辆结构和性能参数的通过性指标,并通过圆锥透度计获得描述地面土壤力学特性的圆锥指数CI,最后建立圆锥指数CI与车辆通过性指标之间的经验公式。1977 年,圆锥指数法被国际地形车辆系统标准协会采用[71]。1979 年发布的北约参考机动性模型(NRMM)[72]以及经更新后于1992 年发布的NRMMⅡ[73],均将圆锥指数CI作为评估军用装备越野通过性的关键指标。近期,捷克国防大学研究分析了圆锥指数CI对坦克越野机动性的影响,并利用CPT描绘了大区域范围的履带车辆越野速度分布图[74]。但是,利用静力触探技术解译地面力学特性不够迅速,难以应对瞬息万变的战场环境。同时基于圆锥指数CI的经验评估方法,缺乏理论模型描述地面土壤力学特性与车辆通过性之间的关系。
综上,静力触探在传统的岩土勘探领域有成熟的应用,而在行星地质探测、车辆地面力学等领域仍有巨大的潜力。未来,随着大规模的行星载人登陆、基地建设和资源开发等任务的陆续开展,大型静力触探设备将会发挥重要作用。同时,下一代北约参考机动性模型(NG-NRMM)将在静力触探技术的基础上,建立通过地面承压、剪切等力学特性评估车辆通过性的理论模型[75-78]。
2.2 动力触探
2.2.1 动力触探技术发展概述
动力触探主要有两种测试方式:一种是用一定质量的击锤,从规定高度自由落下,击打插入土中的探头,测定使探头贯入一定深度所需的击打次数,通过次数评估土壤强度特性。其根据探头形状可以分为管状的标准贯入试验(Standard Penetration Test,SPT)和圆锥动力触探试验(Dynamic Cone Penetration Test,DCP)。另一种方式是在圆锥静力触探的基础上发展而来的自落式动力触探(Free Fall Penetrometer,FFP),它在一定高度下自由下落,并以一定的初速度贯入土体,通过传感器测得贯入过程的加速度和贯入阻力等数据,反演土壤的物理力学参数。
目前的SPT 和DCP,主要通过大量试验数据建立土壤强度特性的经验性解译公式,对于难取样的砂性土、碎石土及静力触探难以贯入的土层,该技术有明显的优势。
FFP 最早可追溯 至1967 年,Scott[80]研制了加速度监测取样器,首次提出仅依据加速度确定土体物理力学特性的方法。但这种早期FFP 只能进行单一加速度测量,参数解译精度不够,限制了其应用。后来纽芬兰纪念大学研制了锤击式触探仪,可以获得贯入过程中的加速度、锥尖阻力和侧壁摩擦阻力[81-82]。近年来,德国不莱梅大学海洋研究中心先后研发了多种可同时测量加速度、锥尖阻力、侧壁摩擦阻力和孔隙水压力的FFP,如长矛形的“FFCPT”[83]、“LIRmeter”[84]和满足流体动力学设计的鱼雷形“Nimrod”[85]。Morton 等[86]基于全流触探技术研制了球形FFP,可测量加速度和角速度。经过半个世纪的发展,目前的FFP 设备有着轻便化、数字化、多参数测量、高精度、高数据采集频率等特点。
2.2.2 动力触探试验仪器组成与原理
SPT 的探头是管状的,击锤质量为63.5 kg,落距为76 cm,以探头贯入土体30 cm 的击数N作为表征土壤承载力强度的指标[87]。DCP 根据击锤质量、落距的不同可分为轻型、重型和特重型,标准贯入试验和圆锥动力触探试验,如图10所示。针对DCP 的三种圆锥动力触探类型的设备规格,铁道部曾在《铁路工程地质原位测试规程》(TB10041-2003)中做了规定,如表3[88]。

表3 圆锥动力触探设备类型及规格Tab.3 DCP equipment type and specification
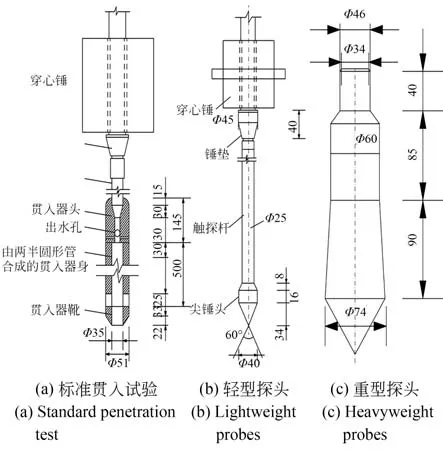
图10 标准贯入试验和圆锥动力触探试验[87]Fig.10 SPT and DCP[87]
SPT 与DCP 的基本原理可以从能量的角度进行阐释:在贯入过程中,动力触探的锤击能量一部分用于克服土体对探头的贯入阻力做功,属于有效能量;一部分能量转化为探杆和土壤自身的变形能;还有一部分能量由于击锤与探杆的非弹性碰撞、探杆与土壤的摩擦而耗散。引入有效能量的转化效率η,则根据能量守恒[88]:
其中:ps为总比贯入阻力,e为每击贯入度,m和H分别为击锤质量和落距,A为探头截面积。
FFP 是在静力触探技术的基础上发展而来,其基本原理与静力触探类似。FFP 的探头形状主要为长矛形探头、符合流体动力学特性的鱼雷形探头和球形探头3 种,如图11 所示[89-91]。早期的FFP 只安装了加速度传感器连续测量实时加速度,球形自落式触探仪也只有加速度传感器和角速度传感器。目前的长矛形和鱼雷形FFP 则在加速度传感器的基础上,加装了尖端阻力传感器、侧壁阻力传感器和孔隙水压传感器。

图11 3 种FFP 探头形状Fig.11 Three FFP probe shapes
相比于静力触探,FFP 的操作更简单,无需额外的加压系统提供探头贯入土体所需的外力,只需通过小型起吊机和缆绳,将FFP 自一定高度自由释放后贯入土体,如图12 所示,因此能够快速地进行大范围的岩土勘探。

图12 球形FFP 测量湖底沉积层[92]Fig.12 Spherical FFP measures sedimentary layers of lakes[92]
2.2.3 动力触探技术的工程应用
SPT 和DCP 在岩土原位勘测中应用十分广泛,主要评估黏性土、粗颗粒土以及卵石土等类型土壤的地基承载力,目前该技术发展成熟而被列入相关的岩土原位勘探规范。赵昭熔等[88]基于动力触探试验与平板载荷试验对比分析的数据,总结了DCP 在碎石类土和砂土中确定地基承载力的经验公式与模型数据库,圆砾、卵石土的变形模量Es的经验公式与模型数据库,以及在中砂至碎石土中击数与地基承载力深度修正系数之间的经验关系。
DCP 在行星表面力学特性探测领域也有不少应用。为了重返月球,NASA 和HoneyBee Robotics 公司在圆锥动力触探技术的基础上进行改进,研制了冲击式触探仪(Percussive Dynamic Cone Penetrometer,PDCP),如图13 所示。PDCP 使用轻巧紧凑的高频低振幅冲击结构代替笨重的击锤,满足了行星探测工程中对设备重量的要求,同时探杆的高频振动使得贯入土体所需的力减小为原来的1/40[93-94],并可达到3 m 的贯入深度,解决了圆锥透度计和SRP 贯入仪贯入月壤深度较浅的问题。

图13 安装在NASA Ames K10 无人星球车上的PDCP[93]Fig.13 PDCP installed on NASA Ames K10 unmanned planet vehicle[93]
针对小行星表面力学特性探测任务中的零重力或微重力环境,探杆贯入时不能给着陆器过大的反作用力,否则会导致着陆器摆脱小行星的引力,故PDCP 也不满足要求[95]。在动力触探原理基础上研制的低速贯入仪(Low Velocity Penetrometer,LVP),传递给着陆器的反作用力小于3 N,解决了该问题[95]。LVP 的核心部件由插入土壤的圆柱形套管、可上下移动的冲击锤和支撑块3 部分组成,其基本原理是依靠弹簧对冲击锤进行周期性储能,利用冲击锤释放后获得的动能,敲击圆柱形套管,从而实现LVP 的周期性间歇贯入,最后到达预定贯入深度,并根据搭载的传感器解译星壤的力学特性[96-97],如图14(a)所示。LVP 在行星表面力学特性探测中应用广泛,如NASA K10 无人月球车搭载的LVP(图14(b))、俄罗斯的火卫-步兵任务搭载的穿透式贯入仪(CHOMIK)[98]、欧洲航天局MUPUS 彗星探测地质穿透器[99]、鼹鼠KRET[100]月球探测器等均基于LVP 装置开发。
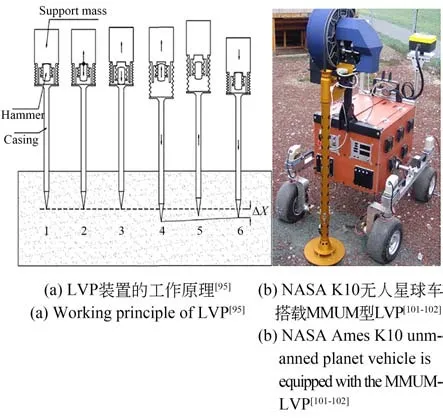
图14 低速贯入仪Fig.14 Low velocity penetrometer
FFP 具有操作流程简便、经济、能对大范围内海底土壤进行快速勘探等优势,因此在海洋岩土工程中应用广泛。FFP 可解译海底饱和软黏土的不排水抗剪强度Su并对海底沉积物进行分类,为港口与海上石油钻井平台的锚泊系统、海底管道等海洋工程提供岩土勘察数据。其中,动力贯入锚(Gravity Installed Anchors,GIA)是一种基于FFP 的原理研制的海上石油钻井锚固装置,一般内置加速度传感器,通过在一定的高度自由下落获得初速度后贯入海床土中,依据传感器输出的加速度时程曲线准确计算贯入深度,从而估算系泊力。目前常用的GIA 有鱼雷锚(图15(a))和OMNI-Max 锚(图15(b))两种,其中鱼雷锚由Petrobras 公司于1996 年提出,长度一般为12~ 15 m,直径1 m 左右,重量500~1 000 kN;OMNI-Max 锚由Delmar 公司在2007 年设计,外形主要为3 块呈120°角分布的锚板,比鱼雷锚提供的系泊力更大。

图15 两种动力贯入锚Fig.15 Two types of GIA
FFP 也曾被尝试用于行星表面力学特性探测领域。基于FFP 工作原理的动能侵彻式贯入仪,先被部署在轨道探测器上,然后与探测器分离,经过空中下落、制动减速、姿态调整等阶段后,最后以一定的速度贯入到星表预期深度,进而通过传感器的测量数据解译星壤剖面的力学特性。截至目前,国际上已有3 款动能侵彻式贯入仪进行了探测任务:1996 年俄罗斯的火星Mars96 探测器搭载了两个动能侵彻式贯入仪[103](图16),1999 年美国的火星探测器搭载两个Deep Space 2 动能侵彻式贯入仪[104],2004 年日本的月球Lunar-A 探测器搭载3 个动能侵彻式贯入仪[105]。然而,这些贯入仪均未成功取得星壤表面力学特性,经分析,可能是由于贯入仪在飞行姿态控制、结构材料强度和内部传感器可靠性等方面,还不足以避免高速贯入时强冲击作用的影响,导致了探测任务的失败。

图16 Mars96 搭载的动能侵彻式贯入仪Fig.16 Kinetic energy penetration type penetrator equipped on Mars96
综上,SPT 和DCP 通过击数评估土壤承压特性等,在岩土工程勘探中,基于工程实测数据建立了大量的经验公式。PDCP 和LVP 轻便且具备较好的贯入能力,因此在近年来的月球和小行星探测任务中被广泛应用。FFP 主要应用在海洋岩土勘探领域,能快速探测海床土的不排水抗剪强度。在FFP 基础上研制的动力贯入锚,通过测量贯入海床土的深度来估算系泊力;而动能侵彻贯入仪因为系统可靠性不足,在几次行星探测任务中均未成功完成探测计划。
最后,对本章所介绍的静力触探和动力触探设备进行归纳和总结,如表4。
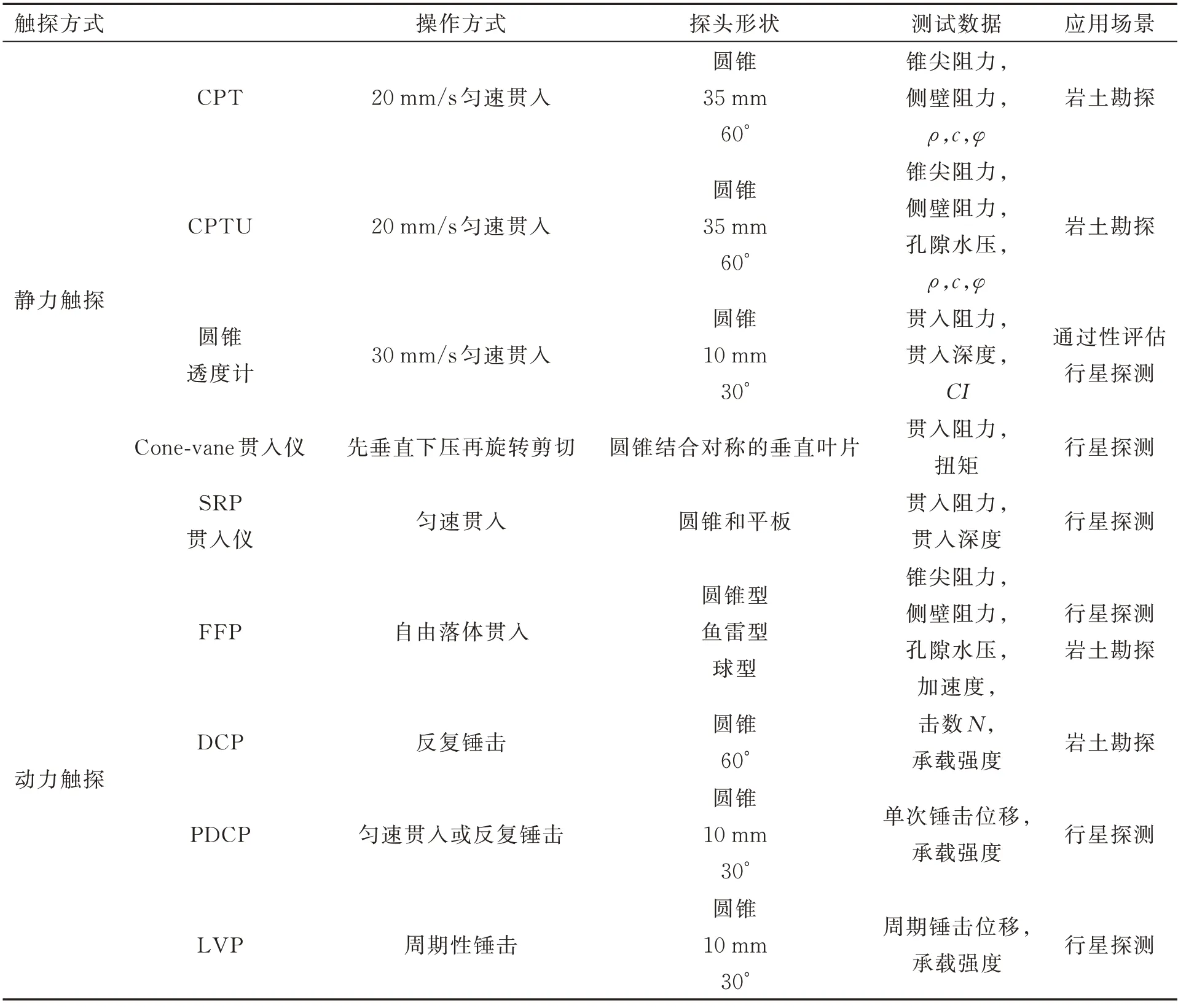
表4 静力触探与动力触探对比Tab.4 Comparison of static penetration and dynamic penetration
3 贯入机理研究进展
利用土壤原位触探技术探测土壤的物理力学参数,需要建立唯象模型将直接测量的贯入阻力与土壤的物理力学参数建立关联。CPT 的发展较为成熟,众多学者基于CPT 的贯入机理开展了大量研究,取得了丰富的成果。FFP 是在CPT 的基础上发展而来的新型技术,由于其属于动态贯入,贯入机理较CPT 更加复杂,相关的研究仍需进一步完善。全流触探技术也是在CPT上发展而来,其探头形状与CPT 不同,但贯入机理相似。标准贯入和圆锥动力触探试验仅通过击数来评估土壤特性,众多学者多依靠现场实测数据来建立参数解译方法,经验性较强,难以围绕贯入机理开展深入研究。本章将针对CPT 和FFP 这两种土壤原位触探技术,系统地总结其贯入机理研究进展。
3.1 圆锥静力触探贯入机理
在工程应用中,利用CPT 技术评估土壤的工程特性大多是基于工程实测数据和经验或半经验公式,缺乏对贯入机理的深入认识,且局限于特定环境下的土壤,不具备普适性。同时,CPT 贯入土体过程中因受到锥尖阻力、土壤的变形过程和应力状态等影响而较为复杂,为贯入机理的认识带来了极大的困难。
研究发现,在黏性土中,CPTU 经孔压和土体上覆应力修正后得到的qnet通常与土体不排水抗剪强度Su之间存在着线性关系[108]。在砂土中,锥尖阻力qc通常与锥尖处的围压σi成线性关系[109]:
其中:Nc,Nq分别为黏性土和砂土的锥尖阻力系数。可见,准确地确定锥尖阻力系数是认识贯入机理的关键。
3.1.1 理论分析方法
CPT 贯入机理分析的理论方法主要有承载力理论、准静态孔穴扩张理论、应变路径法和点位错理论[8]。
(1)承载力理论
承载力理论的基本思想是把探头贯入看作一个地基承载力问题,假设锥尖阻力等效为土中圆形基础的破坏荷载,并采用极限平衡和滑移线两种方法来对锥尖阻力进行分析。
极限平衡法是在假设破坏模式的基础上,通过分析土体的整体平衡状态确定破坏荷载,从而得到锥尖阻 力。如 图17 所 示,Terzaghi[110]、Hu[111]、Vesic[112]、Biarez 等[113]提出了4 种典型的破坏模式。黏性土中,Meyerhof[114]采用图17(b)所示的破坏模式得到锥尖阻力系数Nc与锥尖角α的关系,Durgunoglu 和Mitchell[115]采用图17(d)的破坏模式并引入形状参数λ,导出了Nc的理论解。在砂土中,Janbu 和Senneset[116]采用图17(c)所示的破坏模式,并引入塑性角β(塑性破坏面与水平面的夹角)来刻画砂土的破坏规律,得到砂土锥尖阻力系数Nq与土的有效内摩擦角φ′及β的关系,Durgunoglu 和Mitchell[115],Chen 和Juang[117]采用图17(d)所示的破坏模式,通过引入经验性的形状参数,得到了Nq与φ′的函数关系。

图17 承载力理论假定的4 种破坏模式[119]Fig.17 Four modes of destruction assumed by bearing capacity theory[119]
滑移线法是通过建立滑移线网络,结合Mohr-Coulomb 准则或Tresca 屈服准则来求解土的塑性平衡微分方程、确定破坏荷载,从而得到锥尖阻力。Sokolovskii[118]针对砂土建立滑移线,分析得到Nq与滑移线场中角度δ1、δ2、ω1、ω2之间的函数关系。
刘松玉等[16]总结了上述黏性土和砂土中锥尖阻力系数的理论解,如表5 所示。

表5 锥尖阻力系数的承载力理论解[16]Tab.5 Bearing capacity theoretical solution of cone tip resistance coefficient[16]
(2)准静态孔穴扩张理论
孔穴扩张理论起始于1945 年,Bishop 等[120]研究锥形弹体贯入金属靶体问题时,提出准静态下的圆柱形与球形孔穴扩张模型。Chadwick[121]将准静态孔穴扩张模型应用到理想土体材料,结合Mohr-Coulomb 屈服准则,得到了土壤径向位移的表达式。CPT 贯入土体过程中探头挤压周围土体产生一个圆柱形或球形孔穴,该理论认为在弹塑性介质中产生一个孔穴所需的压力与在相同情形下扩展一个相同体积的空洞所需的压力相等。故先将基本方程(平衡方程、几何方程和土壤本构方程)结合土壤破坏准则及边界条件求解孔穴极限扩张压力,进而可获得锥尖阻力。
Ladanyi 和Johnston[122]基于球形孔穴扩张 理论,采用相同直径的球体代替实际的圆锥探头,假定极限扩张压力与锥尖阻力满足如图18(a)所示的静力平衡关系,分别得到了黏性土与砂土中锥尖阻力系数与土体刚度指数Ir或静止土压力系数K0、有效内摩擦角φ′等指标的函数关系。Vesic[123]根据图18(b)的土体破坏模式,基于球形孔穴扩张理论分别得到黏性土与砂土中锥尖阻力系数的半经验公式。Baligh[124-125]假设黏性土为各向同性、并且不考虑自重,屈服条件满足Tresca 准则,采用圆柱形孔穴扩张理论得到锥尖阻力系数的表达式,但是Yu 和Mitchell[119]认为该表达式高估了锥尖阻力系数。Yu 等[126]认为在探头贯入黏性土的过程中,土壤呈稳态流变状态,由此采用圆柱形孔穴扩张理论获得了探头光滑和粗糙时的锥尖阻力系数。Salgado 等[127-128]通过如图18(c)所示的近似滑移线分析,基于圆柱形孔穴扩张理论,得到砂土锥尖阻力系数的函数。Yasufuku 和Hyde[129]根据图18(d)的土体破坏模式,基于球形孔穴扩张理论,得到了砂土锥尖阻力系数的解析解。
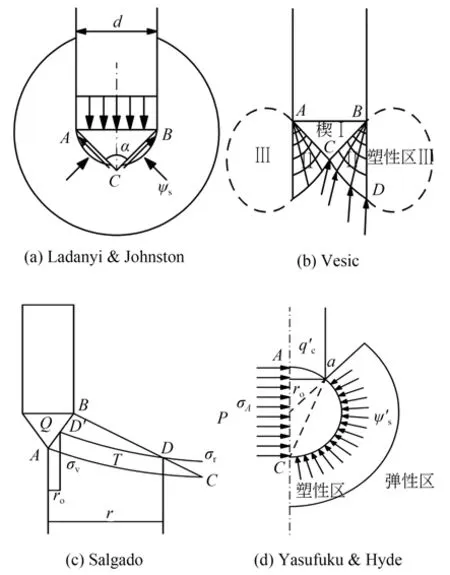
图18 锥尖阻力与孔穴极限压力之间的关系[119]Fig.18 Relationship between the cone tip resistance and the ultimate pressure of the hole[119]
刘松玉等[16]综述了上述在黏性土和砂土中,基于准静态孔穴扩张理论的锥尖阻力半经验公式和解析解的研究进展,如表6 所示。

表6 锥尖阻力系数的准静态孔穴扩张理论解[16]Tab.6 Static cavity expansion theoretical solution of the cone tip resistance coefficient[16]
(3)应变路径法
1986 年,Levadoux 等[130]、Baligh 等[131]提出应变路径法,研究饱和黏土中CPT 的深层贯入阻力机理。该方法将贯入过程中的CPT 看作静止,将塑性变形的土体看作是绕CPT 流动的一个定常流场,通过对流场进行积分获得应变路径,并根据土体的本构关系、初始条件以及边界条件得到应力场,进而获得锥尖阻力。
Baligh 等[132]采用简化的桩基分析方法将探头几何形状做近似处理,得到贯入阻力系数与土壤刚度的关系,如式(9)所示。Teh 和Houlsby[133]采用实际的探头几何形状,通过有限差分法求解控制方程,得到贯入阻力系数与土壤刚度的关系如式(10)。
(4)点位错理论
位错的概念源于材料科学,是指晶体材料的一种内部微观缺陷,其对材料的物理力学性能有着极大影响。由于运动点位错与探头贯入土体存在一致性,Cleary[134],Lee 和Elsworth 等[135-136]用点位错理论分析了探头贯入土体时的锥尖阻力。
Elsworth[137]基于位错理论,考虑土体部分排水,得到锥尖阻力的表达式:
其中:cv为固结系数,μ为动态黏性系数,vu为不排水条件下的泊松比,k为渗透系数,B为孔压系数。
以上4 种理论方法常被用来分析CPT 贯入时的锥尖阻力。其中承载力理论能满足探头贯入时的平衡方程及土体破坏准则,适用于浅层土体贯入问题,但忽略了贯入过程中土体刚度、压缩性及探头周围土体的初始应力状态对锥尖阻力的影响,导致理论解有一定偏差。砂土中,锥尖阻力系数的理论解与实验符合得较好;而在黏性土中,理论解较实验值偏低。孔穴扩张理论考虑了贯入过程中土体的弹塑性变形、应力状态的变化,但简化了土壤的材料特性及非均匀性,对于复杂地质环境中的应用还有待进一步研究。应变路径法可以考虑土体在贯入过程中复杂的变形历史,适用于饱和黏性土,但对于砂土,贯入时的流场难以准确刻画,应变路径法并不适用。同时应变路径法并不能完全满足平衡微分方程,需进一步结合有限元分析得到更真实的应力场分布[138]。点位错理论适用于饱和黏性土壤,可考虑贯入过程土体的部分排水,而前3 种理论分析方法只能假设土体不排水或完全排水。但另一方面,点位错理论将土体视为弹性材料,并将点位错简化为无尺寸的点,不能准确的描述探头贯入时的土体状态。
3.1.2 数值模拟分析方法
针对静力触探贯入过程开展数值模拟研究,有助于揭示静力触探的贯入阻力机理。本文仅针对有限元方法(Finite Element Method,FEM)和离散单元法(Discrete Element Method,DEM)进行介绍。
(1)有限元法
有限元法可以准确地模拟静力触探探头的几何形态,设置土体和探头间的表面摩擦,且保证区域整体和局部均满足平衡方程,通常与孔穴扩张理论、应变路径法等理论分析方法相互结合。针对静力触探模型简化的不同,可分别开展小变形分析和大变形分析。
小变形分析是通过假设探头进入一个预先成形的孔中,土体的应力状态仍处于它的初始应力状态,网格划分结束后,执行贯入过程的增量塑性破坏计算,对应的荷载就假设等于锥尖阻力[8]。该方法忽略了探头贯入过程中周围土体应力变化对锥尖阻力的影响,同时容易出现网格畸变导致数值不收敛,无法实现连续贯入过程的模拟,与实际情况差别较大。因此采用小变形分析对贯入机理进行研究仅为早期的有限元分析手段。
大变形分析可以考虑探头贯入过程中初始应力状态的影响,且在一定程度上解决了网格扭曲、数值不收敛的问题,目前广泛应用于静力触探贯入机理研究问题。大变形分析方法依据网格处理方式可以分为:拉格朗日法、欧拉法和任意拉格朗日-欧拉法(Arbitrary Lagrangian Eulerian,ALE)。其中拉格朗日法的网格与物质重合,易于处理自由表面荷载,但在土体大变形的情况下,网格仍会畸变。欧拉法的网格固定在空间中,土通过网格“流动”,从根本上解决了网格扭曲问题,但其对运动界面的处理十分复杂。任意拉格朗日-欧拉法,结合了拉格朗日法和欧拉法各自的优点,通过改变物质相对于欧拉网格流动的程度来防止网格畸变。在ALE 基础上发展了耦合欧拉-拉格朗日法(Coupled Eulerian Lagrangian,CEL)与小应变网格重划分-插值技术(Remeshing and Interpolation Technique with Small Strain,RITSS),前者通过改变网格与拉格朗日材料一起运动的程度来防止网格畸变;后者是在网格变形过大之前采用拉格朗日算法,之后通过自适应网格再划分技术生成新网格,并基于插值方法将旧网格材料点的应力、材料属性等映射到新网格[139]。
表7 总结了近年来基于有限元法的静力触探贯入阻力机理研究。

表7 近年来基于有限元法CPT 贯入机理研究Tab.7 CPT penetration mechanism researches based on finite element analysis in recent years

续表7 近年来基于有限元法CPT 贯入机理研究Tab.7 CPT penetration mechanism researches based on finite element analysis in recent years
(2)离散单元法
离散单元法由Cundall 等[140]提出,随后被应用于静力触探贯入机理研究。离散单元法通过建立土体颗粒单元体系的参数化模型,进行土颗粒行为模拟与分析,其单元之间相互作用的力可以根据力和位移的关系求出,而每个单元的运动则完全根据单元所受的力和力矩的大小由牛顿运动定律确定。离散单元法更符合土壤散粒性的特点,能很好地反映土体颗粒尺度的力学特性,被应用于研究CPT 贯入机理中的土体大变形非连续破坏问题。
Huang 和Ma[149]采用二维离散元法,研究了正常固结和超固结土中静力触探的贯入机理,结果表明土的应力历史会影响破坏机理和剪胀特性,且更细的颗粒在贯入时的接触应力更大从而更容易破坏。蒋明镜等[150-151]采用二维离散元法对CPT 贯入机理展开进一步研究,认为粒状材料本构模型应考虑剪胀性、率相关性、颗粒破碎及非共轴性等因素,并总结出试验中粒状材料的主要力学性质。刘笋等[152]在此基础上使用二维离散元软件PFC 并引入微观胶结构接触模型,模拟结构性砂土中的贯入问题,从锥尖阻力、位移路径、力链演化和胶结破坏等方面分析CPT 贯入的力学特性。周健等[153]利用颗粒流理论与PFC 程序,建立了二维离散元模型来模拟贯入过程,研究了K0和超固结比OCR 对锥尖阻力的影响,得到的模拟结果与试验结果较一致,验证了离散元模拟与颗粒流方法结合的可行性。
三维离散元模型相较于二维离散元模型更接近CPT 贯入问题的实际情况,但三维离散元方法所需颗粒数庞大,严重影响了计算效率。Butlanska 等[154]分别建立了全模、1/2 模、1/4 模的三维离散元模型模拟CPT 贯入,并对它们的计算效率进行比较,发现可利用对称性建立局部模型来减小计算量。但局部模型存在严重的边界效应影响,杨彦骋等[155]运用环向周期边界建立了1/4 模的三维离散元模型,消除了边界效应,同时深入分析了探头贯入过程中土体各向异性的演化规律。
综上,基于有限元法和离散单元法对CPT贯入机理进行了大量研究。有限元法能较好地处理贯入过程的土体大变形问题,但有限元法基于连续介质假设,很难反映土体颗粒的细观非连续力学特性。离散单元法以颗粒为单元,并设置土颗粒间的微观作用来模拟土体,能很好地模拟CPT 贯入时土体的微观特性。
3.1.3 试验方法
在早期的工程勘察阶段,国内外学者根据静力触探现场实测试验的数据,通过数值拟合的手段建立了大量的经验公式,如静力触探贯入阻力同土壤的强度特性、变形特性、固结与渗流特性之间的经验关系,刘松玉等[16]、蔡国军等[26-27]对此进行了系统的归纳和总结。
为了进一步研究静力触探贯入机理,国内外开展了较多大型标定罐试验以模拟土的原位测试,不仅可以建立锥尖阻力和土的特性之间的经验关系,而且能够进行机理分析及验证理论分析。标定罐试验自动化程度较高,有着测试的排水条件和应力条件可控的优点,但其尺寸较小,直径、高度一般不超过2 m,多采用微型静力触探探头进行模拟试验。图19 为澳大利亚新南威尔士大学于2010 年设计的一款用于非饱和土的柔性单壁标定罐装置[156]。

图19 新南威尔士大学研制的标定罐[156]Fig.19 Calibration chamber developed by the University of New South Wales[156]
目前基于标定罐试验,已得到大量锥尖阻力与土的物理力学参数(相对密度、摩擦角、状态参数等)之间的经验关系。其中Houlsby 和Hitchman[157]、Jamiokowski 等[158]、Schmertmann 等[159]得到了基于土的相对密实度的圆锥探头系数计算公式,Houlsby 和Hitchman[157]得到了基于土的摩擦角的圆锥探头系数计算公式;Been 等、Yu 等得到了基于土的状态参数的圆锥探头系数计算公式。刘松玉等[16]对上述经验公式进行了汇总,如表8 所示。

表8 基于标定罐试验结果的锥尖阻力经验公式Tab.8 Empirical formulas for cone tip resistance based on calibration chamber test results
标定罐试验是在一定条件下对现场实测的模拟,由于受到土样大小和应力状态的限制,边界效应和尺寸效应将对标定罐试验结果造成影响。
由于标定罐能对水平和垂直边界进行控制,目前研究者共定义了5 种不同的边界条件[160-161],如图20 所示。BC1 的水平和垂直应力边界为常数,应变边界为0;BC2 的水平和垂直应变边界为0,应力边界不设定;BC3 的垂直应力边界为常数,水平应变边界为0,其他边界不设定;BC4 的垂直应变边界为0,水平应力边界为常数,其他边界不设定;BC5 的垂直应力边界为常数,水平应力边界不为常数但可设定,应变边界不设定。Parkin 等[162]针 对BC1、BC3 和BC4 这3 种边界条件,研究了在不同罐锥直径比条件下的标定罐试验对锥尖阻力的影响,发现在BC1 和BC4 两种边界下标定罐试验结果小于实测值,BC3 边界条件下的试验结果大于实测值。

图20 标定罐试验5 种不同边界条件[160-161]Fig.20 Five different boundary conditions of calibration chamber test[160-161]
Schnaid 和Houlsby[163]针对尺寸效应进行 了不同直径比的标定罐试验。结果表明,在密砂和中密砂中极限锥尖阻力随着直径比增大而显著增加,但在松散砂土中该效应不明显。Salgado等[128]在孔穴扩张理论的基础上,对标定罐试验的尺寸效应形成原因展开分析,如图21 所示,随着贯入阻力的增加,孔穴表面的径向应力也增加,导致孔穴周围形成塑性区,往外是非线性弹性区和线弹性区直至标定罐边界,从而导致了尺寸效应。
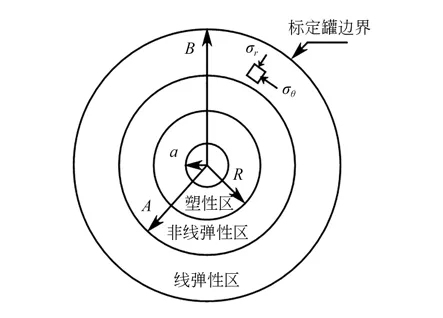
图21 孔穴扩张理论的土体响应分区[128]Fig.21 Soil response partition for cavity expansion theory[128]
3.2 自落式动力触探贯入机理
CPT 是以约20 mm/s 的速度匀速贯入土体,加载过程可看作准静态过程。FFP 贯入过程中的速度远大于CPT,使得探头周围土体发生大变形,而且FFP 为动态贯入是减速运动直至停止贯入,整个贯入过程十分复杂。
Mulukutla 等[164]根据FFP 中加速度传感器测量的数据绘制了归一化的加速度-时间曲线,如图22 所示,整个贯入运动过程分成4 个阶段:(1)碰撞冲击,(2)贯入土体,(3)初始制动及振荡回弹,(4)最终制动。
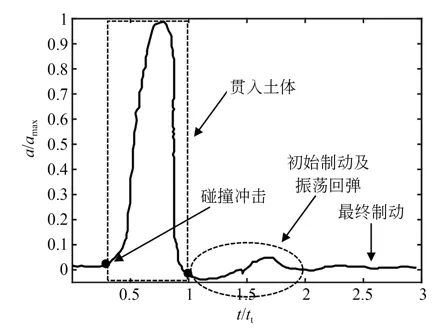
图22 FFP 贯入过程的归一化加速度-时间曲线[164]Fig.22 Normalized acceleration-time curve of FFP penetrate into soil[164]
3.2.1 理论分析方法
对FFP 的贯入机理开展理论分析,首先需要建立FFP 贯入运动过程第2 阶段的动力学方程。
True[165]针对只含加 速度传感器的锥形FFP,研究了FFP 贯入软黏土过程中的受力特性,认为贯入阻力由锥尖阻力Ft、侧壁摩擦阻力Fs、拖拽阻力Fd和土体浮力Fb构成,如图23(a)所示,并基于牛顿第二定律建立FFP 贯入土体的动力学方程,Chow 等[166-167]考虑黏附在FFP 上土体的惯性力,对动力学方程进行了补充:
其中:m为FFP 的质量,m′为随FFP 加速或减速的惯性土壤质量,Ws为FFP 在土体中的浮重。
Morton 等[92,168]针对球型FFP 进行了系统研究,基于牛顿第二定律建立了球型FFP 与土体的相互作用模型,如图23(b)所示,动力学方程表示为:其中:Fss为球体在土中的浮重;FAM为附加在球体上的土产生的惯性力;Fresist为球体的贯入总阻力,即端部阻力与拖拽阻力之和。

图23 FFP 贯入过程受力分析Fig.23 FFP penetration process force analysis
综上,针对FFP 贯入土体过程建立的动力学方程,仍需进一步厘清贯入阻力的作用机制。在CPT 静态贯入过程中,贯入阻力与土体强度参数直接相关,而对于FFP 动态贯入过程,贯入阻力与贯入速度也存在着联系。目前研究FFP 贯入阻力机理主要有两种方法。第一种方法是通过引入与贯入速度相关的应变率效应,将动态的贯入阻力转化为恒定参考贯入速度下的准静态贯入阻力,从而将FFP 的动态贯入问题转化成与CPT 类似的准静态问题。第二种方法是基于动态孔穴扩张理论直接得到贯入阻力与贯入速度、土体强度参数的函数关系。
(1)基于应变率效应修正的准静态分析模型
Dayal和Allen[82]引入经验性的应变率因子fac,以直接将FFP贯入与标准的CPT 贯入进行比较:
其中:K是无量纲因子,在1~1.5 范围内取值;v0=0.02 m/s 为标准CPT 贯入的速度。
Steiner 等[169]在利用FFP 和CPTU 对软黏土和高敏黏土进行对比试验分析时,引入应变率因子fac,将动态的锥尖阻力qd和侧壁摩擦阻力fd分别修正为准静态下的qc和fs:
应变率因子fac是纯经验性的参数,不能从机理上解释贯入速度对贯入阻力的影响。通过对26 种黏性土进行不同速率的加载试验发现,土体强度存在应变率效应[87],即土体强度参数随着加载速率的增加而增大,并引入率效应系数Rf修正应变率效应对土体不排水抗剪强度Su的影响,如式(16)所示。加载试验还发现黏性土的不排水抗剪强度与应变率在半对数坐标下存在线性关系,如图24 所示,故将Rf拟合成对数形式,如式(17)所示[170]:

图24 应变率对26 种黏性土不排水抗剪强度的影响[84]Fig.24 Effection of strain rate on undrained shear strength of twenty-six kinds of clay soil[84]
与之类似,Dayal 和Allen[82]、Einav 和Randolph[171]提出采用幂指数函数和反双曲正弦函数来描述土体强度的率效应,如式(18)和式(19)所示:
韩聪聪[172]通过如图25 所示函数图像比较了以上3 种函数形式的率效应系数Rf,发现当应变率与参考应变率之比在1~103之间时,3 种函数得到的率效应系数Rf基本相同。当应变率与参考应变率之比大于103时,幂指数形式的率效应系 数Rf偏 高,而根据Biscontin 和Pestana[173]的 十字板剪切试验可知,率效应参数β会随应变率的增加而增大,故幂指数形式的率效应系数此时更适合。

图25 3 种土壤率效应系数随应变率的变化关系[172]Fig.25 There relationships between the soil rate effect coefficient and the shear strain rate[172]
Chow 等[166]引入幂指数形式的率效应系数来修正式(12)中的锥尖阻力和侧壁摩擦阻力,如式(20)和(21)所示,并认为锥尖与侧壁处的率效应参数βt、βs不一致。同样,Morton 等[92]也使用幂指数形式的率效应系数修正式(13)中的端部阻力。
其中:用贯入速度与FFP 直径的比值近似表示探头周围土体的应变率,即v/d;Nkt为承载力系数;At和As分别是锥尖和探杆侧壁的表面积;μ是锥土界面的摩擦系数,其大小可近似为土体灵敏度的倒数。
(2)基于动态孔穴扩张理论的分析模型
圆锥静力触探理论分析中采用的准静态孔穴扩张模型未考虑材料的惯性效应,而当孔穴扩张速度(贯入速度)较高时,惯性效应会影响孔穴径向 应力的 计算结果。Hill[174]和Hopkins[175]给出了动态孔穴扩张模型控制方程,研究FFP 的贯入机理。与准静态孔穴扩张理论不同的是,FFP 贯入土体过程中,球形孔穴会以速度V扩展,孔穴周围的土体会形成塑性区和弹性区,如图26(a)所示。将弹塑性边界的扩张速度记为c,则塑性区的范围在区间(Vt,ct)内,而弹性区的范围是(ct,∞)。
Forrestal 和Luk[176-177]基于动态孔穴扩张 理论,针对土壤的动态贯入问题做了系统性研究。其中假设土壤材料为静水自锁的本构关系,根据如图26(b)所示的锥土相互作用关系(锥体贯入过程中所受到的表面法向阻力σn,等于球形孔穴在无限大的土体介质中扩张时的表面径向应力),在分别满足Tresca 准则和Mohr-Coulomb 强度准则的条件下,分析了贯入过程中土壤的动力响应,得到的贯入阻力为:
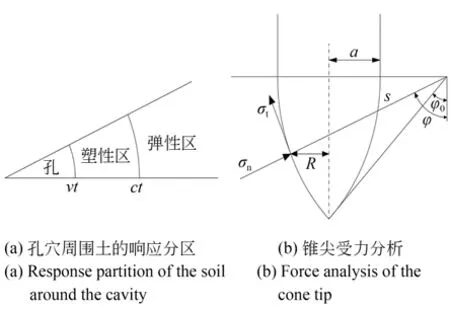
图26 球形孔穴扩张模型[175]Fig.26 Spherical cavity expansion model[175]
其中,αs,βs是与土壤力学特性有关的系数。
在此基础上,Shi 等[178]采用p-α状态方程与Mohr-Coulumb-Tresca 极限屈服准则描述砂土的本构关系与强度准则,建立了考虑砂土压缩性的球形孔穴扩张模型。
综上,基于应变率效应修正的准静态分析模型,其准确性依赖于应变率系数Rf的取值,没能阐述土体率效应产生的机制。而且贯入速度与FFP 直径的比值v/d,不能真实反映动态贯入过程中的土体应变率。基于动态孔穴扩张理论研究FFP 的贯入阻力机理,其准确性依赖于土体塑性屈服准则、本构方程能否真实全面的反映土体材料。目前的研究大多对土体的材料特性进行了简化,未考虑土壤应变率效应、剪胀性和各向异性等因素对结果的影响[179]。但考虑上述因素的影响对屈服准则和本构关系进行修正会增加参数,使得模型得到解析解的难度加大,故如何在兼顾模型求解效率的同时对模型进行修正十分关键。
3.2.2 数值模拟方法
FFP 的贯入速度远大于CPT,土体会发生很大的变形,运动过程也十分复杂。因此,在研究CPT 贯入机理时使用的小变形分析方法不再适用,因为它无法避免网格畸变导致的数值发散。目前用于研究FFP 贯入机理的数值模拟方法主要有大变形有限元分析方法中的ALE 法和CEL法,基于计算流体力学(Computational Fluid Dynamic,CFD)的有限体积法,物质点法(Material Point Method,MPM)等。
Sabetamal 等[180]基 于ALE 方法模拟了鱼雷锚的动力贯入过程,土体本构采用修正的剑桥模型。Carter 等[181]、Nazem 等[182]采 用ALE 方法对FFP 的贯入阻力进行了参数分析,结果与实测试验吻合较好,并与CPT 数值模拟结果进行了对比,验证了应变率参数修正的准静态分析模型的有效性。
Kim 等[107,183-184]和Liu 等[185]使 用CEL 方法模拟了鱼雷锚的动力贯入过程,采用率效应和软化效应修正的理想弹塑性Tresca 屈服准则,研究了土体强度、锚重量、锚长径比、贯入速度等因素对贯入深度的影响,扩展了True 和Randolph 提出的预测贯入深度的理论模型。CEL方法无法准确模拟锚和土的摩擦力,Kim 等[183]使用特征摩擦力进行模拟,但模拟结果会高于实际的摩擦,且无法考虑土体率效应对摩擦力的影响。Liu 等[185]将锚和土的接触模式设置为无摩擦接触,而将实际的摩擦力等效为集中荷载施加在锚上。
Liu 等[185]、Raie 等[186]用CFD 方法,模拟了鱼雷锚的贯入过程,根据模拟结果提出预测贯入深度的模型。其中Liu 等[187-189]假定土体为非牛顿流体,用动力粘滞系数描述土体强度,并考虑土体率效应的影响。同时,在锚的外侧设置5 层总厚度为5 mm 的边界层,通过引入经验参数将边界层处的土体强度进行折减,以此来模拟锚土之间的摩擦力。
除此之外,LS-DYNA 也被用于研究FFP 动态贯入的问题。张金利等[190]基于LS-DYNA 商业软件,采用Soil-and-Foam-Failure 土体模型模拟土体的大变形和失效行为,系统研究了鱼雷锚的长径比、海床土体强度参数c、φ和贯入速度对贯入深度、贯入阻力、加速度等影响。Weiss等[191-192]使用LS-DYNA 对动能侵彻式贯入仪贯入月壤剖面过程进行分析,模型中贯入仪分别以160 m/s、319 m/s 和505 m/s 的速度贯入厚度2 m 的月壤风化层。
有限元方法处理FFP 高速贯入导致的土体大变形问题时,利用网格重划分技术可避免网格畸变,但网格重划分的过程计算量大,且在追踪应力历史相关土体材料的状态变量时会产生误差。有限元方法也难以模拟FFP 在砂土中的贯入过程,这是因为在高速冲击贯入条件下,砂土处于高应力状态,其动态响应十分复杂,排水条件也难以准确刻画。基于这个原因,Zambrano 和Yerro[193]采 用MPM 法研究FFP 在砂土中 的贯入问题。他们采用两种屈服准则(非关联Mohr-Coulomb 准则和应变软化Mohr-Coulomb 准则)来描述砂土的破坏,利用移动网格技术保证了FFP 几何形状尺寸的精确性,并采用摩擦接触算法模拟土与FFP 的相互作用,最后得到的模拟结果与实验吻合。
3.2.3 试验方法
现有的FFP 贯入试验研究多借助现场实测试验与室内模型试验。现场实测试验能得到最真实的原位数据,但针对大型鱼雷锚贯入海床土,现场测试的经济成本往往较高,且容易受到天气等因素的影响。对于室内模型试验手段,一般使用高岭土和钙质土等制备具有相应强度特性的土样,以模拟现场应力条件的软黏土,同时将大型鱼雷锚装置等比例缩小,建立测试数据与缩比之间的相似关系,从而达到模拟现场测试的效果。在室内模型试验的基础上又发展出离心模型试验的技术手段,通过对模型施加离心加速度场模拟特殊的重力条件,并使模型槽内土体与现场的应力条件一致;而普通重力条件下的模型试验通过折减土体强度来模拟现场应力条件。
True[194]开展了大量的现场试验来研究作用在FFP 上的贯入阻力,建立了FFP 贯入的动力学方程。针对不同种类的鱼雷锚在海床中的贯入,De Araujo 等[195]、Lieng 等[196]、Medeiros[197]也开展了相关的现场试验,得到不同土壤中的锚埋深比(锚尖埋深和锚长的比值)。
Chow 等[166]、Steiner 等[198]对FFP 贯入软黏土的过程开展了离心模型实验,试验装置如图27 所示,研究土体率效应对贯入阻力的影响,实验结果表明FFP 侧壁处的土体率效应系数Rf大于锥尖处。O′Loughlin 等[199]通过离心机实验研究了鱼雷锚动态贯入问题,提出了基于能量法预测贯入深度的表达式。此外,许多研究者也通过离心模型实验研究了海底土强度、长径比等因素对鱼雷锚贯入深度的影响。

图27 离心试验装置[167]Fig.27 Centrifuge test device[167]
4 总结与展望
土壤原位触探技术经历数十年的发展,目前已成为重要的土壤勘测手段,下面针对其技术、工程应用及贯入机理研究进行总结与展望。
目前静力触探技术比较成熟,相关测试设备集成度高,具备多种土壤参数解译功能,并开发了数字化的数据采集、传输与处理模块。同时静力触探试验已被列入行业规范,有着标准的操作流程,土壤参数解译结果可靠。然而静力触探技术也面临一些问题,如大型测试系统笨重、操作复杂、耗时长,而便携式测试系统贯入深度浅,导致应用场景受限。自落式动力触探技术作为在CPT 基础上发展起来的新型技术,具有轻便和操作简单等优点,但土壤参数解译精度不高,且在飞行姿态控制、高速冲击下的传感器可靠性、弹体结构的抗冲击强度等方面还面临许多挑战。未来土壤原位触探技术的发展需要重点关注以上的方面,不断提高土壤参数解译的精度。
土壤原位触探技术已广泛应用于许多工程实践领域。在行星表面地质探测方面,基于动力触探的PDCP、LVP 和动能侵彻式贯入仪由于其轻便、操作简单的优点,在目前的探测任务中发展潜力巨大,同时在未来大规模开展行星探测工程中,较成熟的静力触探测试系统也会发挥重要作用。在海洋岩土勘探和车辆机动性评估中,FFP 由于能快速获取大范围内的土壤力学特性,将会是未来的主要测试手段。
目前,针对土壤原位触探技术的贯入机理,已经在理论分析、数值模拟和实验测试3 个层面开展了大量的研究。在理论分析方面,如何准确地刻画探头与土体间的复杂相互作用仍然是研究的重点。在不同的地质环境及冲击荷载作用下,土体将呈现出不同的动态响应及流变特性,损伤演化特征也各不相同,并具有多尺度的特征。准确地抓住土体损伤演化的主要特点将为唯象模型的建立和土体参数的解译奠定基础。此外,多尺度多场耦合的数值仿真模拟将成为一种重要的手段。通过有限元、离散元等数值模拟方法能够处理复杂边界条件的情况,并考虑土体的大变形、非均匀性、各向异性、多相多介质等特点。因此,开展高精度、大规模的数值仿真将为贯入机理的研究提供重要的参考。对于贯入试验,室内模型槽试验将继续在贯入机理研究及理论验证等方面起到重要作用。实验测试的一个重要方面是更精细地捕捉贯入过程中探头附近的土体变形及其流动特征、损伤特征、开裂特征,从而揭示贯入机理的主要方面。随着对于原位触探技术贯入机理认识的不断深入以及新型传感器的发展,土壤物理力学参数的解译也将越来越精准。
