装备野外通行路径优化算法研究进展

常宁东，程鹏达，冯 春，2*，王理想，李玉琼，2*

（1.中国科学院 力学研究所，北京 100190；2.中国科学院大学 工程科学学院，北京 100049）

1 引言

随着科技的进步与军事力量的发展，野外路径优化在军事战场环境分析中的地位日益提升［1-3］。通过野外路径优化技术，可以对战场环境进行模拟分析，以此指挥军事装备、机器人、智能设备和人员的行动［4］。目前，野外路径优化也广泛应用于野外灾情救援、军事定向越野和自驾旅游等。确定高效可行的野外路径并进行路径优化可以保障野外活动的准确开展，缩短军事装备、救灾装备和旅游装备的野外行驶时间，降低军事活动和救灾避险活动中的损失［5］。

与城市道路优化不同，野外环境下的道路不具备道路结构化及交通规则信息；基于既有道路的路径优化是典型的线状网络优化问题，而野外环境的通行路径优化则是典型的面状优化问题。同时，野外环境中具有多种阻碍装备正常运行的障碍物和未知威胁，由于地表属性较为复杂，会存在坑洼、泥泞的道路，因此会对装备的行进造成多种影响或阻碍。

野外环境下路径优化是指在有界空间内根据感知系统输入的野外环境信息，在考虑到环境和装备等多种约束条件的基础上，生成从初始位置到达指定目标的高效安全的优化行驶路径。在工程装备在野外复杂地面上行进路径的选择和优化过程中，土地类型（农业、灌木丛、森林、湿地、城市等）、地形特征（坡度、表面粗糙度、丘/沟障碍物的大小和间距、树木/植被茎的大小和间距等）、地面力学特性（弹塑性、摩擦角、粘聚力等）以及装备特征（编队、重量、履带、轮式、轮腿式、轨道、叶片和尖齿等）等直接影响装备的通行速度，进而影响装备在复杂地面行进的路径选择和路径优化。

目前大多数研究均围绕既有城市道路优化展开，针对野外环境下的路径优化研究相对较少［6］。鉴于此，本文对野外路径优化的不同算法进行综述，对不同算法的优势与不足进行了阐述，并对野外环境下的路径优化进行了展望。

2 野外环境建模方法综述

为对野外路径进行合理优化，需事先收集野外环境的相关信息，对已有的空间信息进行环境建模，因此对环境准确、合理地建模是路径优化的重要前提。目前常用的野外环境建模方法有可视图法、Voronoi 图法、拓扑法和栅格法［7-11］。

2.1 可视图法

可视图法由Lozano-Pérez［12］提出，该方法首先确定环境中的障碍物，将障碍物表示为多边形连接区域，根据与各障碍物顶点之间的可视情况进行判断［13］。对相互可视的顶点之间的连线赋予权重形成可视边，顶点的集合与可视边的集合共同组成了可视图，如图1 所示。

图1 可视图法示意图［14］Fig.1 Schematic diagram of viewable method［14］

由于可视图法原理较为简单，该方法的实现较为方便，但仅适用于障碍物顶点数目较少的方法。当障碍物的顶点数目较多时，将会产生许多无关可视路径，大大降低可视图构造的效率，同时影响搜索算法的收敛性。依据可视图法搜索到的最短路径往往较为粗糙，与真实最短路径存在偏差，且缺乏灵活性，无法用于三维优化［8，15-16］。

2.2 Voronoi 图法

Voronoi 图法［17］是一种避免路径与障碍物之间碰撞的方法，该方法首先设置系列控制点，即生成元，以此生成元为核向外扩张直至与其他多边形相碰为止，将所有生成点作为顶点形成三角形的外接圆，以此得到每个多边形的所有边界信息，再沿着多边形的边界寻找一条无碰撞的路径，如图2 所示。

图2 Voronoi 图法示意图［9］Fig.2 Schematic diagram of Voronoi method［9］

Voronoi 图法是一种不依赖于空间坐标的临近模型，且其计算出的路径安全性较高，但其计算量十分大，仅适用于简单环境模型，且得到的路径常常不是最优路径［9，18］。

2.3 拓扑法

拓扑法地图来源于图论，为数学的一个分支［19］。拓扑法将事物用节点来表示，节点与节点之间的关系用边来表示，在拓扑地图中只关心它们之间的连接关系，而不考虑长短等信息，因此忽略了大量的环境信息［20］。该方法首先将环境空间划分并建立特征网，在形成的特征网中搜索路径，如图3 所示。

图3 拓扑法示意图［7］Fig.3 Schematic diagram of topological method［7］

拓扑法省去了直接测量环境数据的麻烦，具有建模方便、计算成本耗费较小等优点，但拓扑法对于相似的地点难以进行区分，并且难以得到详细信息［21-23］。

2.4 栅格法

栅格法根据野外探测的雷达数据将空间划分为大小相同的矩形栅格，再依据传感器得到的信息对栅格内的情况进行实时判断，如图4所示。

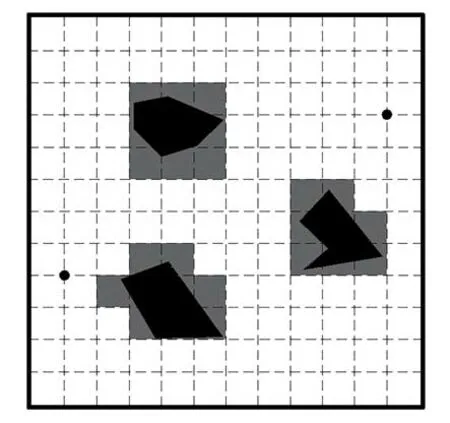
图4 栅格法示意图［7］Fig.4 Schematic diagram of grid method［7］

由于栅格法实现简单，在一定程度上可以保证环境信息的精度，所以得到广泛的应用。建立栅格地图时，栅格的大小是一个关键问题。当栅格过大时，虽然数据处理量得到减少，缩短了路径的搜索时间，但环境信息的精度会因此受到损失，最终得到的路径常常不是最优路径；当栅格过小时，虽然精度得到了提高，但数据量将会提高，对于较大空间环境难以进行路径搜索，因此需要选择适宜的栅格数量与栅格大小。该方法可以结合其他搜索算法进行优化，但无法对动态障碍进行处理［24-26］。

综上所述，可视图法与Voronoi 图法适用于简单的模型，可视图法会导致路径搜索时间较长，Voronoi 图法进行路径优化时计算量也较大，因此对于复杂的模型将会耗费大量的成本和资源。拓扑法无法在障碍物密集的环境下进行路径规划，而栅格法相对建模简单，目前得到广泛的应用。

3 单装备路径优化算法

野外路径优化即基于野外环境模型，在给定起点和终点后，寻得一条最优的无碰撞路径。根据野外环境是否已知，可将野外路径优化划分为全局优化和局部优化。全局优化方法需要事先得到野外环境信息，根据起点和目的地得到一条完整的全局路线，同时可以为局部路线提供参考。局部优化方法则是根据装备上的传感器等设备获取野外信息，从而进行实时的调整。这两种方法的区别仅在于环境信息是否已知，两者按照优化算法都可以大致分为图搜索法、随机采样法和智能优化算法。

3.1 图搜索法

图搜索法首先建立环境的栅格地图，再将环境信息赋予每个网格，在此基础上进行野外路径的寻优工作。该算法主要包括Dijkstra 算法［27］、A*算法［28］、D*算法［29］及其推广。

3.1.1 Dijkstra 算法

Dijkstra 算法［30］由荷兰学者Dijkstra 提出，也称狄克斯特拉算法。该算法通过计算一个节点到其他所有节点的最小代价并不断递进以寻得起点与终点之间的最优路径［31］。

首先假设各节点为V，令连接两节点之间的带权矩阵Cost［i，j］代表节点Vi和Vj之间的权值。令起始点为VS，D［i］为起始点VS到每一个节点Vi的最小权值，并令S为已经找到的起点最短路径的各终点集合，S初始值为S=｛VS｝，具体流程如下：

（1）寻得初始最短路径的终点Vj，即D［j］=min｛D［i］｝，此时S=S∪｛Vj｝；

（2）寻得起点VS到集合V-S的任一节点VK的最短路径。如果D［j］+Cost［j，k］＜D［k］，则进行下一步。

（3）令D［k］=D［j］+Cost［j，k］，不断重复上述步骤，以此得到最短路径节点的集合。

Dijkstra 算法可以进行一个目标到多个目标的路径寻优，但是其具有一定的盲目性，寻优速率较慢，不具有启发性［32］。

3.1.2 A*算法

A*算法［33］在Dijkstra 算法的基础上，在搜索过程中引入了启发值，以此使得搜索具有一定的目标性，其中A 为这类算法的统称，星号代表启发式的功能，又称A-Star［34］。

启发值作为一个预估值，估计每个节点与目标之间的距离，因此具有一定的误差。其公式为：

其中：f*（n）为起点到n点的最小代价估计，g*（n）为起点到n点的最小代价，h*（n）为启发函数。

虽然A*算法提高了运算速度，但由于启发值与实际代价存在差异，将会导致寻得的路径并不一定为最优路径，同时其无法适应快速变化的环境，不具有实时性，同时A*算法只适用于具有位置信息的地图。鲍久圣等［35］使用指数函数加权和三次样条插值的方法，对A*算法进行改进，并在井下巷道内进行全局路径优化仿真。王洪斌等［36］通过改进A*搜索算法，实现了一次优化能够达到多个目标点。谭雁英等［37］基于A*算法的优化，使得无人机路径优化可以适应圆形、凹/凸多边形危险/威胁区域同时存在的情形。

3.1.3 D*算法

D*算法［38］源于Dynamic A Star，是在A*算法的基础上进行发展，主要克服了A*算法无法实时适用环境的缺点。D*算法将终点作为搜索起点，首先将所有未知环境假设为畅通的，随着搜索的进行，部分自由区域被发现为障碍，从而该点与终点之间的代价增加，并向相邻节点进行扩展，对权值发生变化的节点进行处理，从而减小了工作量，增加了寻优速度［39］。

D*算法具有计算数据少、可实时更新和较为简易的优点，此外，学者们也对其进行了不断改进。Koenig 等［40］提出了D*Lite 算法，进一步提高了D*算法的速率，得到了广泛应用。史久根等［41］基于CA 模型对D*算法进行改进，得到的路径与障碍物保持安全距离，缩短了计算时间。黄鲁等［42］基于懒惰视线算法与距离变换相结合的方法，对D*Lite 算法进行了改进，得到了更为平滑与安全的路径。

综上所述，对于传统主要路径优化算法，Diljkstra 算法和A*算法为正向搜索过程，需要预先得到全局信息，只能进行静态优化。D*算法在上述两种算法基础上进行改进，不需要环境所有信息，可以进行实时动态优化，更适合具有不确定性的野外环境。

3.2 随机采样法

随机采样法首先在优化空间内随机采样以此建立空间上的连通性，该方法能够适应高维且较为复杂的环境，并且适用于装备在非完整约束的环境路径优化问题，主要包括概率地图法和快速搜索随机树法，以及一些其推广算法。

3.2.1 概率地图法

概率地图法（Probabilistic Roadmap Method，PRM）将连续空间的路径优化问题转化为拓扑空间的优化问题，该方法首先根据随机采样的方法生成空间的概率地图，并随机挑选一个采样点判断是否发生碰撞，之后选择局部快速优化器，以此将新搜索的无碰撞节点与之前的路径相连，最终形成一个从起点到终点的无碰撞路径［43］，具体流程如图5。

图5 概率地图算法流程Fig.5 Flow chart of probabilistic roadmap method

概率地图法实现较为简单，且具有很好的实用性，但由于搜索过程中采样具有随机性，因此最终输出结果无法保证为最优路径。曾国奇等［44］基于PRM 算法提出网格概率地图法，实现了无人机的多约束路径优化。马江涛等［45］提出一种基于局部二次学习概率路径图算法，通过二次局部学习，提高了算法的求解效率以及路径图质量。

3.2.2 快速搜索随机树法

快速搜索随机树法［46］（Rapidly-exploring Random Trees，RRT）由Lavalle 提出，该算法不需要对环境空间进行预处理，且可以考虑非完整约束、动力学约束等，可以解决复杂环境下的路径优化问题。

该算法首先根据初始节点qstrat构建随机搜索树T，不断迭代进行随机采样选择状态节点qrand，通过遍历得到距离初始节点qstrat路径最短的qnear，再输入控制集U，根据状态转换方程进行积分，从而得到qnew；不断重复上述过程，最终搜索到终点qend，再由终点qend反溯到初始节点qstrat，从而得到最终的优化路径。

RRT 算法由于采用均匀随机采样，因此会造成一定的资源浪费、收敛速度变慢，同时由于随机性，最终生成的路径并不平滑。在此基础上产生了一系列衍生算法，如RRT-Connect 和RRT*等。Lavalle 和Kuffner 等［47］提出了Bi-RRF 算法，提高了搜索速率。Karaman 等［48］通过添加父节点重选机制，减小了生成路径时的抖动。

综上所述，基于随机采样的路径优化算法不受限于环境信息，适用于高维度空间。PRM 和RRT 算法注重寻优的快速性，最终寻得路径为可行路径，但并不一定为最优路径。随机采样法生成概率地图时可以考虑动力学约束，对于野外环境下的装备运行，在加入动力学约束之后，路径优化算法将会更为平滑，更符合实际运行过程。

3.3 人工势场法

人工势场法是通过模拟电荷在电场中的运动实现寻优，其基本思想是将装备视为势能场U中的一个质点，使得障碍物与装备带同种电荷而产生斥力，终点与装备带异种电荷而产生引力，因此在某点q的总势场U如下式所示：

其中：Uatt为引力势，Urep为斥力势。

该路径优化问题即寻找势场全局最小值的问题，因此不需要对环境进行地图建模。寻求全局最小值最简单算法为梯度下降法，将势场U的负梯度视为一个广义力，即F=-∇U，令装备从起点开始运行，沿着梯度反方向行走，直到梯度为0 停止。该方法优化的路径较为平滑，但是由于算法本身的原因而存在一定的问题：（1）当引力和斥力恰好大小相等、方向相反时，装备容易陷入局部极小值或产生振荡；（2）若目标点附近存在障碍物，当装备靠近障碍物时斥力将会无限大，导致装备无法到达目标点；（3）当装备距离目标点较远时，引力将会特别大，障碍物造成的斥力相对较小，因此可能会在路径上碰到障碍物。除此之外，对于野外环境下的装备路径优化，传统人工势场法由于将装备视为质点，因此无法考虑运动学和动力学等约束。

针对上述问题，Li 等［49］为每一个点赋予随机的力场向量，使得陷入局部极小值的设备可以摆脱局部极小点，但该方法容易导致装备在极小点产生振荡。Connolly 等［50］提出引入调和函数来定义势场函数，以此保证除目标点外不会产生第二个极小点，解决局部最小值的问题。韩尧等［51］引入了角度与速度调节因子，得到了更为真实的无人机飞行轨迹。田洪清等［52］提出PRM 和APF算法相结合的人工势能场-概率图法，考虑了车辆动力学特性，提出了多目标的野外环境路径优化算法。

3.4 智能优化算法

随着人类对自然界认知的深入，受自然规律或物理现象的启发，不断衍生的多种随机搜索算法，统称为智能优化算法，比如蚁群算法、遗传算法和神经网络算法等。这些算法可以直接应用于路径优化问题，也可以与上述传统方法相结合进行应用。

3.4.1 蚁群算法

蚁群算法［53-54］对蚂蚁群的爬行行为进行模拟，蚂蚁在经过一个未知路口时，各蚂蚁会根据路径的长短释放信息素，信息素的量随着路径的增加而减小，因此蚂蚁群可以根据信息素的量的大小寻得最优路径。

对于处于节点i的蚂蚁，其选择的下一个节点是具有随机性的，根据局部信息素和启发值给出：

其中：l为任意可能的取值；allowed（k）表示蚂蚁k可以访问的节点集合；τij（t）为t时刻弧（i，j）的信息 素；ηij为 启发值，ηij=1/dij；α和β为相对重 要性，均不小于0。

对于节点i上第k个蚂蚁的转移概率为：

当蚂蚁群的所有蚂蚁完成各自的路径后，每个蚂蚁k在其经过的路径上所释放的信息素量为：

其中：T（k）（t）为t次迭代后的TSP 解；Q为参数，一般可取1；Lk（t）为求解的路径长度。

通过式（5）更新规则对信息素进行更新，再进行不断迭代更新，最终获得最优路径。

蚂蚁算法在计算规模较小的问题时具有较强的优势，但对于计算量较大的问题则容易陷入局部最优解。为解决上述问题，万旭等［55］基于最大-最小策略，降低了蚂蚁算法陷入局部最小值的可能，并将其应用于有时间窗装备路径问题。孙焘等［56］基于蚂蚁算法，增加了变异和最优保存的操作，提高了算法的收敛性。胡中华等［57］将导引因子引入到状态转移策略中，减少了蚂蚁局部搜索的盲目性。

3.4.2 遗传算法

遗传算法［58］（Genetic Algorithms）基于自然界中物种的进化过程，是一种主要用于寻求最优解的方法，通过对自然界亲代与子代之间的遗传机制和进化理论进行模拟，提出一种可以对数据进行并行计算的寻优理论。遗传算法不受搜索空间的限制、运算简单、收敛速度快，适用于解决复杂和非线性等较难问题［59］。

遗传算法是由Holland［60］提出的一种自适应的全局优化概率算法，该算法模拟个体组成为群体的整体学习过程。遗传算法首先将问题转化为遗传中的基因编码问题，生成任一初始群体，再根据适应度函数对各基因序列进行优化，进行复制、交叉、变异和选择等操作，不断重复迭代使得群体逐步进化，最终求得问题的最优解，其流程图如图6 所示。

图6 遗传算法流程图Fig.6 Flow chart of genetic algorithms

遗传算法作为一种并行运算方法，具有较快的计算速度，且不需事先得到问题的全部信息，在全局路径优化中得到广泛应用。虽然其具有较强的全局搜索能力，但是在局部搜索中存在缺陷，容易陷入局部最小值［61］，且计算速度较慢，容易产生“早熟”现象。郎茂祥等［62］将爬山算法和遗传算法结合，在一定程度上克服了遗传算法局部搜索能力不足的问题。张潜等［63］构造了一种随机开关，以此控制遗传算法中的变异操作，避免陷入局部最小值的问题。欧丽珍等［31］基于Dijkstra 对遗传算法进行改进，实现了定向野外中的多目标路径寻优过程。

3.4.3 神经网络算法

人工神经网络［64］（Artificial Neural Network）是一种基于人脑和神经系统处理方法的数学模型，通过模拟神经网络中的神经元信息输入、传递和处理的方式，形成具有自适应能力的体系，通过建立网格之间的映射关系，结合生物学的神经网络相关理论，如图7 所示。人工神经网络在对数据进行分类、识别、回归、预测和组织等方面［65］具有强大优势，其主要优点如下：

图7 人工神经网络算法网格图Fig.7 Grid diagram of artificial neural network algorithm

（1）人工神经网络采用并行计算的信息处理方式，在大量的神经元信息并行处理时具有速度快、效率高的优点；

（2）人工神经网络每一个神经元可以接受其他神经元大量的输入，进而处理信息并输出信息，实现对下一个神经元的信息传递，网络之间的相互影响可以实现从输入状态到输出状态的非线性映射，因此可以处理非线性问题，同时具有容错性和鲁棒性；

（3）人工神经网络以权值的形式将处理的数据信息储存下来，因此具有较高的记忆能力；

（4）人工神经网络通过学习和训练得到网格中的权值和阈值，因此具有极强的学习能力和自适应能力；

（5）人工神经网络采用分布式存储知识，信息分布在整个系统当中，因此具有联想功能。

在路径优化中，神经网络算法可以通过分类结果对优化算法进行引导，大大提高了计算速度，并且在局部优化中，可以通过神经网络的映射关系对动态环境做出快速反应，但其也存在易陷入局部最小值的问题［66］，且只适用于环境条件已知的情况，无法处理动态障碍物。Araujo 等［67］提出一种可裁剪的模糊自适应共振理论神经网络结构，以此实现了动态更新和局部优化。禹建丽等［68］基于人工神经网络算法和模拟退火温度定义路径能量函数，实现了机器人路径的优化。狄勇等［69］提出一种模糊神经网络的避障策略，通过模糊神经网络搜索可行节点来实现避障功能。

综上所述，智能优化算法大多具有并行运算的优势，提高了计算时间，具有较高的自适应性和鲁棒性，因此具有良好的实时性。

3.5 考虑动力学约束的优化算法

目前大多传统路径优化算法大多仅考虑了运动学约束，而很少考虑动力学约束。野外存在复杂的地形条件，同时野外环境下的装备将面临高度非线性的约束，相对于城市道路，野外装备将会面临倾倒、滑移和颠簸等问题，因此在路径优化中考虑动力学约束至关重要。

在野外路径优化前，需要考虑复杂场景数据，如积雪深度和密度、冻结或解冻深度、最大制动加速度、驾驶员反应时间、安全系数、可视度、障碍物几何参数和有无沙子等。对于地形数据，需要考虑地面状况、土体类型、土体湿度、土体强度、基岩埋深、表面粗糙度、障碍物的几何特性和植被分布情况等。对于装备数据，需要考虑装备尺寸、轴或转向架等组件、驾驶员的位置、中心、悬架、轮胎的尺寸、履带、传动系统和雪链等。在此基础上，对于任意给定的区域，首先对道路和野外环境分别进行建模，之后采用单独的地形数据定义机动特性。对于复杂地形力学建模需有效的模拟装备与土壤之间的力学交互特性，现对于复杂地形力学建模方法［70］包括连续介质模型，如有限元法（Finite Element Method，FEM）；粒子模型，如离散元法（Discrete Element Method，DEM）、光滑粒子流体力学法（Smoothed Particle Hydrodynamics，SPH）和物质点法（Material Point Method，MPM）。

目前国内对装备在野外环境中通行的动力学效应研究较少，王学宁［71］基于Bekker 理论，考虑了坦克履带的滑动与横摆，建立了坦克的动力学仿真模型。李佳圣等［72］考虑了底盘悬架和轮胎结构，建立了越野车辆底盘的动力学模型，但仅考虑了车辆的俯仰角速度。刘凯等［73］建立了考虑道路倾角的动力学模型，并提出了基于零力矩点的车辆侧倾的约束，可以有效地防止车辆发生倾倒侧翻。

国外考虑装备动力学的路径优化方法中，最具有代表性的为北约参考机动模型（NATO Reference Mobility Model，NRMM），早期模型以经验公式为基础，且只考虑了仰俯角，未考虑转向/转弯、胎面/粗面和左右两侧地形不对称等对装备稳定性的影响，无法满足现代装备仿真的要求［74］。在此基础上研发的下一代北约机动参考模型（Next Generation NATO Reference Mobility Model，NG-NRMM）通过将地理信息系统（Geograpic Information System，GIS）软件和多体、基于物理学车辆动态建模和仿真软件进行融合，利用地面力学来适当评估装备-地形间的软土（可变形的土地）交互，可获取软土对装备机动性的影响效应［75］。

综上所述，路径优化算法逐渐趋于成熟，不同的算法具有不同的优点和缺点，应针对不同问题选择适宜的算法，以此来提高路径优化的效率。对于图搜索法，Diljkstra 算法和A*算法虽然搜索效率较高，但是容易得到非最优解，同时仅适用于静态环境的优化，D*算法基于上述两种算法，实现了实时动态优化，可以在充满不确定性的野外环境进行适时调整。相对于图搜索法，随机采样法不受限于环境信息，可以处理更复杂的环境模型，同时可以考虑装备的动力学约束，但也存在寻得路径为非最优路径的问题。对于智能优化算法，大多具有较好的鲁棒性和稳定性，具有并行处理问题的功能，但容易陷入局部最优解从而无法收敛。智能优化算法适用较为广泛，现在受到学者们广泛的研究和应用。

4 多装备的路径优化算法

目前针对野外环境下多装备路径优化算法的研究较少，但对于既有道路环境下多车辆路径优化算法较为成熟，因此可以参考VRP 问题中的相关优化算法。按照多装备的路径特点可大致分为四类：多目标装备路径优化算法、多基地装备路径优化算法、多类型装备路径优化算法和带时间窗的路径优化算法［76］。

4.1 多目标装备路径优化算法

在多目标路径优化算法中各个子目标之间是相互矛盾的，无法令多个子目标同时得到最优解，往往一个子目标的改善会引起其他子目标的恶化，因此只能寻得一个中间值，使得每一个子目标尽可能达到最优。目前的研究方法主要可以分为两类：精确算法和启发式算法。

4.1.1 精确算法

精确算法指整数优化法和动态优化算法等数学优化算法。整数优化法［77］通过构造问题对应的整数优化模型，再利用MATLAB 等数学软件进行求解，但该方法只能得到一个精确解，主要应用于规模较小的多目标路径优化问题。动态优化算法［78］是一种在不同阶段求得最优解的一种算法，按照路径的方向可分为下降路径和上升路径。下降路径将问题分为多个子问题，再分别求解这些子问题；上升路径先求解可能用到的所有子问题，基于求解结果构造上级更大问题的解。

Hu［79］将多个目标整合为单个目标，采用整数线性优化实现了多目标集装箱供应链的路径优化。李媛媛等［80］在动态优化算法中引入了惩罚函数，实现了机器人的动态路径优化。周睿慜等［81］提出上升路径和下降路径相结合的动态优化算法，提高了机器人路径优化的效率。虽然精确算法耗费时间较少，但由于精确算法原理的局限性，无法解决较为复杂和规模较大的多目标路线优化问题，因此启发式优化算法应用更为广泛。

4.1.2 启发式优化算法

由于多目标路径优化问题的目标函数和约束函数常常为非线性的，并且一些问题规模较大，其复杂程度也随之增加，一般的最优算法无法进行求解，而启发式算法针对此类问题求解效率较高。

元启发式算法作为一种通用的启发式算法，在启发式算法的基础上结合了随机方法和搜索算法等。主要包括遗传算法、蚁群算法、禁忌搜索算法、模拟退火算法和粒子群算法等。

Long 等［82］基于遗传算法实现了多目标的车辆分配和访问顺序，并考虑了客户预定等因素。张涛等［83］将启发式规则和遗传算法相结合，实现了多目标的地震救援路径优化。陈治亚等［84］以路径最短和均衡度为目标，采用非支配排序策略，实现了考虑随机需求的多目标路径优化。裴小兵等［85］基于模拟退火算法，结合记忆函数，并利用聚类分析初始化状态种群，实现了城市物流车辆多目标路径优化。蒲兴成等［86］将蚁群算法和粒子群算法相结合，引入反向学习策略，并对算法的权重和学习因子进行改进，避免了早熟现象。

4.2 多基地装备路径优化算法

多基地装备路径问题指有多个装备基地可以为目标服务，因此要求对各个基地发配的装备和行驶路线进行合理安排。对于多基地装备路径优化问题，需要在满足约束的条件下，使得路程成本降为最低，同时还需要进行基地的选择和优化处理，因此求解存在一定的难度。

目前针对多基地的装备路径优化研究较少，大多聚焦于单个出发点的问题。雷坤等［87］采用End-to-End 深度强化学习的方法，利用改进图注意力网格作为编码器，实现了任意数目车场的车辆路径优化问题。Alinaghian 等［88］提出一种自适应大邻域和变邻域搜索相结合的混合算法，以降低车辆数和运输成本为目标，实现了多车场多隔间的路径优化问题。杜茂康等［89］通过改进的多染色体遗传算法，实现了车载无人机起飞、降落等任务。戚远航等［90］以离散蝙蝠算法为核心，结合泰森多边形的初始化策略加快算法，加快了多车场车辆路径问题的计算速度。

4.3 多类型装备路径优化算法

在军事活动中往往需要多种装备的运行，确定装备的类型、尺寸和数量是节约时间和成本的关键。按照装备的类型，可以将装备路径优化问题分为单类型装备和多类型装备，单类型装备问题需要假定装备的类型、尺寸、最大载重、最大行驶距离和成本等都相同，而多类型装备问题装备类型和成本等往往都不同，如军事活动中往往需要装甲车和坦克车等共同运作。

针对多类型装备的路径优化问题，国内外学者开展了一定的研究。柳伍生等［91］提出无人机与车辆相联合的模型，基于带末端优化的模拟退火算法求解了路径优化问题。Ostermeier 等［92］发现采用单隔间和多隔间混合车队进行杂货配送时，可以有效地降低成本。姚竟发等［93］提出联合收割机多机无冲突协同作业路径优化算法，实现了收割机的多机协同作业。阮贵航等［94］基于滚动优化和分散捕食者猎物模型算法，结合鲸鱼优化算法实现了多机器人全覆盖路径优化算法，减少了机器人行走路径。

4.4 带时间窗的路径优化算法

在野外环境下进行物资运输、军事演习和救援救灾等活动时，往往需要在特定时间段内完成任务，因此需要多个装备同时运行。带时间窗的路径优化算法即在装备路径优化算法中施加时间窗约束，时间窗为任务要求的一个时间区间，因此对于带时间窗的路径优化算法，在对装备进行空间上的路径优化基础上，还需要对各个时间段进行合理的安排与分配。

参照多隔间车辆路径问题（Multi-compartment VRP，MCVRP）划分的原则，根据是否必须严格按照时间窗的规定，可以将带时间窗的路径优化算法划分为带有硬时间窗的路径优化算法和带有软时间窗的路径优化算法［76］。对于带有硬时间窗的路径优化算法必须严格按照规定时间段进行优化，而带有软时间窗的路径优化算法允许早于或晚于规定的时间段，但需要承担相应的时间窗惩罚成本。Cordeau 等［95］利用禁忌搜索算法实现了带时间窗的车辆路径优化。王超等［96］基于回溯搜索优化算法，实现了带时间窗和同时送取货的路径优化。柴获等［97］基于蚁群算法，提出了综合考虑目标、时间窗和信息素等信息的状态转移概率公式，实现了双目标带时间窗的路径优化问题。

综上所述，由于军事活动和救灾活动等要求，需要多装备同时在野外环境下进行运作，因此针对其路径特点进行相应的路径优化，可以保证高效的完成目标，但目前针对多装备的路径优化问题研究相对不足。多装备在野外环境进行运作时，势必会遇到动力学约束改变等问题，如前车经过后土壤更为夯实、相邻车辆在转弯时的相互影响和前车行驶速度等影响，当前对于多装备的动力学研究较少，但其是多种装备共同行驶时亟待解决的问题。

5 结论与展望

复杂野外环境下的路径优化是开展军事活动、实现军事装备运行的关键技术。野外环境不同于既有道路路径优化，其存在多种影响装备运行的障碍物、威胁物和野外坑洼。本文就野外环境下的建模方法和路径优化方法进行了调研与总结，对各方法的适用环境与利弊进行了阐述，针对野外路径的路径优化提出以下几点展望：

（1）智能性。目前人工智能方法在其他领域受到学者们的广泛应用，是今后路径优化算法的研究方向之一。由于人工智能方法需要大量的数据样本支撑，在野外环境中应用存在一定的难度，因此需要建立开源的野外环境的数据集。

（2）动力学耦合。对于在野外环境运行的装备，其受到多方面因素的影响，如地面平整度、土壤质地和气候天气等，环境较城市道路更为复杂，装备在行驶过程中可能会发生颠覆、倾倒等现象，因此需要将动力学约束纳入路径优化模型，在路径优化过程中需要保证装备的正常行驶，可以通过建立路径优化与地形力学相耦合的平台，进一步对路径进行优化评估。

（3）协同性和异构性。为完成特定的军事任务或生产任务等，往往需要多个装备协同运行，同时需要多种类型装备，如战斗车辆与运输车辆共同运行。目前对于野外环境下多装备路径优化研究较少，同时多装备的路径优化约束更多，问题更为复杂，会产生相应动力学问题，因此需要深入开展多装备路径优化问题研究。