基于SVR算法的光伏电站工程造价预测研究
2023-04-10李东伟姚雅婷周子东
李东伟,姚雅婷,周子东
(1.中国电建集团华东勘测设计研究院有限公司,浙江 杭州 310014;2.河海大学商学院,江苏 南京 211100)
0 引 言
当前,我国企业在海外光伏电站项目建设领域已经有一些经验,但由于海外工程不确定因素较多,且业主要求严苛,竞争者众多,企业仍有进一步提高效率、提升竞争力的需求。在工程管理中,工程造价的计量工作贯穿工程建设的全寿命周期,为工程建设提供随时的价格服务,是成本管控能否成功的关键。我国传统的工程计价主要将工程定额作为设计、咨询单位进行工、料、机消耗量计算的依据和标准。传统的定额体系存在着管理途径有限、与实际工程情况脱节、缺乏现代理念等缺陷,计价人员在依据定额测算工程造价的同时,需结合自身经验及市场变化,耗时较长且对于计价人员计价水平的依赖较大,有较强的不确定性,影响企业的成本管理和控制。由于影响工程造价的因素错综复杂,建筑工程造价测算涉及到众多领域的知识。对建筑工程的造价进行建模预测,可帮助造价人员提前了解工程造价,并在项目建设过程中时刻把握各部分造价的变化。因此,对建筑工程造价管理的一个重点研究方向即建立能进行快速、准确预测的模型。
引入机器学习方法建立数学模型,将大大提高效率,在没有时间进行详细估算、信息不充分等特殊情况下,提供一种快速估价的方法。为此,本文以海外光伏电站工程为研究对象,引入支持向量回归(SVR)算法,对该工程造价的分解及对其影响因素进行深入分析并预测总造价,为系统研究光伏电站各部分造价及总造价提供了思路,同时也拓展了支持向量回归算法在工程造价预测领域的应用。
1 研究设计
1.1 研究方法
对比发现,支持向量回归(SVR)算法能在小样本情况下表现出较好的效果[1],适合海外光伏电站项目较少的现状。采用支持向量回归算法构建预测模型遵循的一般步骤见图1。

图1 构建预测模型的步骤
支持向量回归算法是支持向量机算法在处理回归问题时的变体,核心在于确定1个与所有样本点之间的距离总体最小的超平面[2]。其基本思想是将核函数加入SVM算法中,使非线性问题变为线性问题,从而降低算法的复杂性,且得到与原来一样的结论[3-4]。算法的性能受核函数类型的较大影响,常用的类型主要有多层感知机核函数、多项式核函数和高斯径向核函数[5]。其中,高斯径向核函数中的参数较少,空间复杂度较低,且非线性能力强,同时易实现SVR的优化过程[6-9],本文模型拟采用高斯径向核函数。
由于支持向量回归算法对样本要求较高,本文引入逐步回归法进行特征选择以精简变量体系,降低变量间的多重共线性。其基本思想是:若判定输入变量偏回归平方和显著,则将其放入回归模型,并且每增加1个新变量都会对之前已经引入的变量进行检验,删除不显著变量,保留显著变量。为保证效果,本文模型采用向前逐步回归法和向后逐步回归法相结合的方法。
1.2 变量体系
考虑到机器学习算法小样本的特点,样本质量对预测结果的影响较大,变量体系的设计尤为重要。因此,需对光伏电站工程进行深入分析,并结合光伏电站结构特点,进行变量体系设计。
1.2.1 光伏电站造价划分及输出变量的确定
本文在实践经验的基础上,借鉴了传统划分方式及学者马翠萍[10]、鲁正[11]的优秀成果,最终将光伏电站工程造价划分为3大类7个模块,见表1。本文所指电站造价仅包含发电系统和升压变电站(简称升压站)2部分及其他必要费用,将其总造价划分为光伏场区采购及建安工程费用、升压站采购及建安工程费用、其他费用等3大类,不考虑间接费。由于电站设备及材料购置费、土建费用及安装调试费用(以下将三者统称为“建安工程费”)占到80%以上,而根据相关计价标准规定,将建安工程费作为基准,乘以取费费率即可得到其他部分的价格。因此,主要测算光伏场区和升压站的设备采购和建安工程费。

表1 光伏电站造价模块划分
根据理论和实践经验,将光伏电站场区的重点部分单独提取作分析,每个模块再划分基本项作为模型输出变量。考虑将占总造价比例较大的分部工程(组件、结构构件、电路系统)单独提取出,结构构件即用以支撑光伏组件稳定的设备,包括支架和桩基础;电路系统是光伏发电系统中电力的主要电力设备,包括逆变器和箱式变压器。考虑海外项目海运费用占电站总造价的比例较大且变化多、风险大,将物流费用单独进行预测。项目管理及一般费用、勘测设计费均与电站总容量有较大相关性,因此进行统一预测。最终,提炼出如表2所示6个需要进行预测的部分作为本文模型的输出变量。剩余基本项由于透明易得,均作为已知项直接给出。

表2 输出变量及其内涵界定
1.2.2 影响因素分析及输入变量的确定
在分析光伏电站结构的基础上,通过专家访谈、调查问卷等方式,得出影响海外光伏电站造价的所有因素并转化为相应的变量,进一步将所有输入变量划分为普遍输入变量和特殊输入变量,得到本文的输入变量体系,并对变量内涵进行界定。输入变量及其内涵界定见表3。将所有变量汇总,各变量间关系见图2。

图2 变量间关系

表3 输入变量及其内涵界定
2 预测模型构建
2.1 样本准备
2.1.1 数据来源
本文以某公司的海外光伏电站项目为例构建预测模型,国别因素对应的项目所在国人均GDP数据来源于国家统计局,其他项目数据全部来自该公司海外光伏电站项目的实际报价表。从报价表中分别摘取所需数据并进行整理,对于报价表中少量缺失的数据,结合工程实际进行计算填充。本文分析以美洲区域数据为例,选定12个项目作为样本,其中,哥伦比亚6个,智利2个,巴西、巴拿马、多米尼加、秘鲁各1个,项目规模最小50 MW,最大409 MW。
2.1.2 数据预处理
采用机器学习算法构建预测模型时,数据是模型学习规律的重要参照,样本数据本身的质量直接影响到模型最终的预测效果。因此,在构建模型前对样本数据进行预处理,以保证模型性能。
首先,考虑到支持向量回归算法对于输入数据中的缺失值比较敏感,在收集数据后,针对由于数据可获得性而出现的缺失和异常数据,根据造价人员的专业建议进行填补和修正,得到了较为完善的数据。其次,作为样本数据,各输入变量值的量纲可能会有所不同,若差别较大,算法会有选择地忽略量级较小的变量数据,或减小其比重,进而影响到数据分析的结果和算法的预测效果。因此,本文在构建模型之前,先对数据进行了归一化处理,以符合分析要求,保证得出的变量关系不受影响。采用python 3.9内已包含的min-max标准化法代码包,实现min-max标准化方式处理样本数据。具体公式如下
(1)
式中,x为待标准化的样本值;x′为样本值标准化结果;n为样本数量;x1,x2,…,xn为变量x对应的所有样本值。经过数据填补、修正及标准化处理,得到了标准、完善的样本数据,为构建预测模型奠定基础。
2.2 模型构建
2.2.1 逐步回归分析
本文将向前逐步回归法和向后逐步回归法结合做双向逐步回归,将前文分析得到的变量体系,采用python 3.9实现。主要步骤及实现见图3。
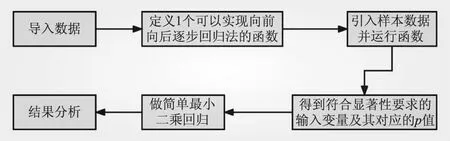
图3 逐步回归分析步骤
(1)导入数据。采用python 3.9中的pandas库导入excel数据。
(2)手动定义1个逐步回归函数,使其同时具备向前筛选和向后筛选的功能,设置逐步回归函数的主要代码如下
def stepwise(x,y,alpha_in=0.15,alpha_out=0.20)
上述代码中,x为所有输入变量构成的数据框架;y为输出变量。设可选入的输入变量的显著性水平上限为alpha_in,本文将其设置为0.15,即显著性水平小于0.15的变量均可选入模型,剔除变量的显著性水平下限为alpha_out,本文设置为0.20,即显著性水平大于0.20的变量均应从模型中剔除。向前筛选功能的实现:用所有还未选入的输入变量与选入变量的子集建立一元或多元线性回归方程,当所有回归方程中得到的最小的p值(回归方程自变量系数的p检验统计量的值)小于引入变量的显著性水平α(alpha_in)时,则作为引入变量。向后筛选功能与向前筛选恰好相反,先将所有变量作为选入变量,再逐步剔除,当其中最大的p值大于剔除变量的显著性水平α(alpha_out)时,则剔除。
(3)引入数据。采用函数得出重要输入变量,将步骤(1)中导入的数据应用于步骤(2)定义的函数中,即
result=stepwise(x,y)
(2)
(4)用上一步中得到的重要输入变量进行最小二乘回归分析,得到模型逐步回归结果,见表4。
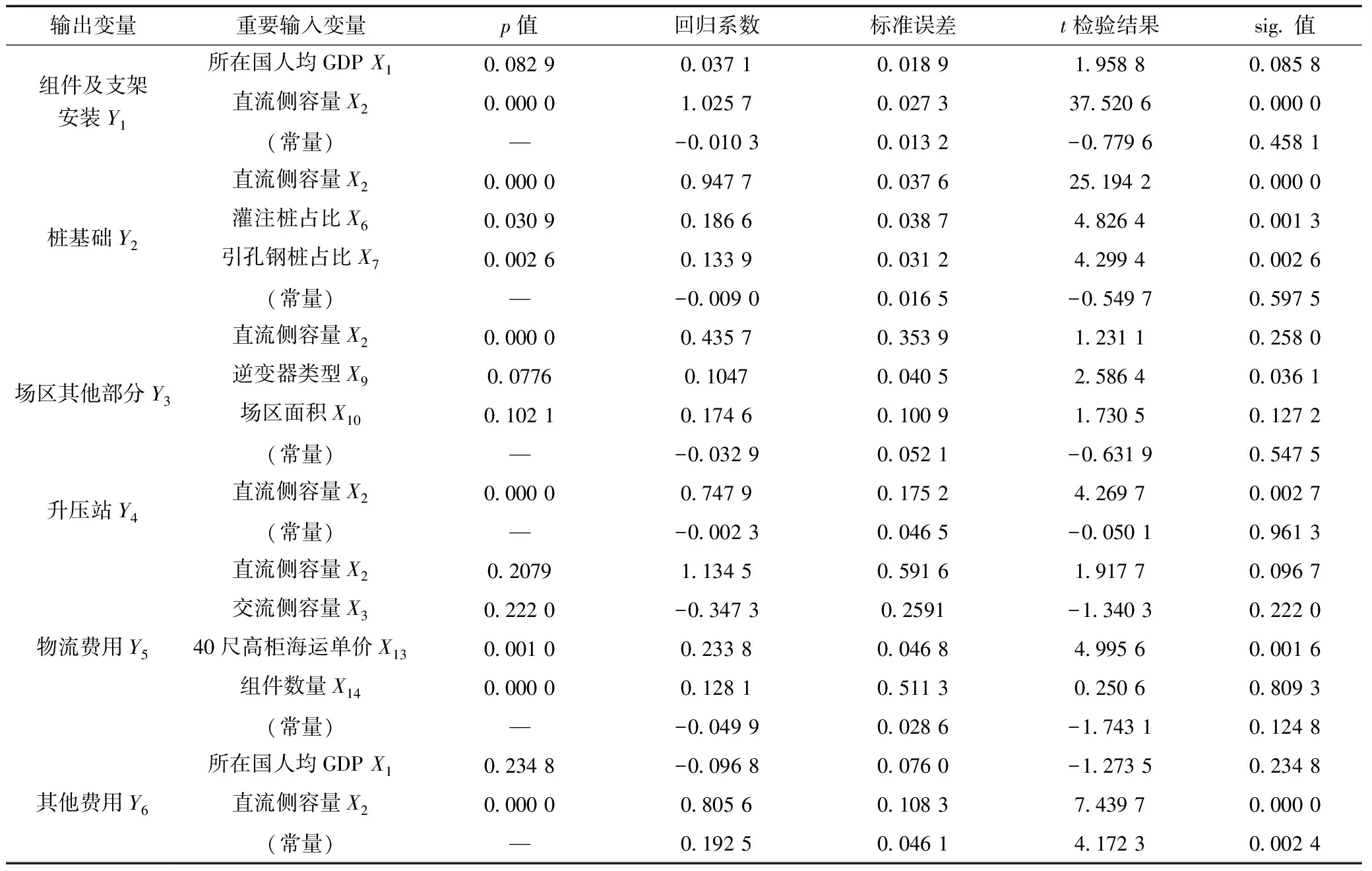
表4 逐步回归方法筛选变量结果及其回归系数
经过向前向后逐步回归法的筛选,保留了p值小于0.10的显著变量,考虑到有些变量对模型的影响可能较复杂,同时保留了p值位于0.15~0.25之间的变量,最终每个输出变量只保留1~3个输入变量,避免了输入变量之间的多重共线性对模型的影响,精简了变量体系,提高了模型精度和泛化能力,得到的参数估计值均与实践经验相符。同时也发现,在采用逐步回归方法做简单回归分析得到的结果中,模型表现不及预期,究其原因,一方面,由于样本数量少,不能满足回归分析的样本要求;另一方面,各个部分的影响因素对其产生影响的途径和方式比较复杂,不一定是简单的线性关系,在无法确定其关系时,回归分析性能受到影响,难以得出有效的结果。
2.2.2 支持向量回归
采用向前向后逐步回归法对变量体系进行进一步精简后,将剩余的显著变量输入SVR模型中进行分析。由于海外光伏电站样本数量限制,可充分利用SVR模型优秀的小样本学习能力,得出更为精确的预测结果,同时保证模型的泛化能力。根据SVR算法的基本原理,构建基于向前向后逐步回归法的SVR模型,并采用python 3.9实现,主要步骤见图4。

图4 SVR算法应用步骤
(1)划分训练集和测试集数据。本文直接引用python 3.9的sklearn库中内置的模型实现训练集和测试集的划分。考虑样本有限,需要适当控制2个集合的样本数量,以保证模型结果的准确性。本文将test size参数设置为0.20,即将全部样本的20%用作测试集,80%用作训练集,即
x_train,x_test,y_train,y_test
train_test_split(x,y,test_size=0.20)
(2)数据归一化。防止数据量级差别大影响模型预测精度。
(3)构建SVR模型。本文采用高斯径向核函数进行输入变量的映射,以解决非线性问题。python 3.9中自带有SVR模型包,用如下代码可得到
from sklearn.svm import SVR
svr=SVR(kernel=‘rbf’,C=le3,gamma=0.10)
上述代码中,rbf即高斯径向核函数;C和gamma是模型中的参数。C表示惩罚因子,代表着模型对离群数据的重视程度,趋近无穷时模型会过拟合;gamma是核函数的核系数,gamma越大,模型越容易出现过拟合和泛化误差,即对训练集的拟合程度越好,而对测试集的拟合优度越差。经过多次尝试,本文最终设置C为1e3,gamma为0.10时,得到了较好的效果。
(4)利用训练集数据训练模型,即
svr,fit(x_train,y_train)
(5)采用测试集数据检验模型性能。本文采用R2拟合优度、均方差MSE、平均绝对误差MAE评估模型效果。
(6)对模型结果进行反归一化处理,得到最终预测值。并将预测值和真实值进行对比分析。
本文对预测结果的具体值进行分析,采用R2拟合优度、MSE、MAE分别衡量6个模型的预测精度,评价结果见表5。从表5可知,拟合优度大于0.90,表明模型预测精度较高;MSE和MAE均小于0.10,表示模型预测的误差较小,本文构建的基于逐步回归法的SVR模型的预测精度和泛化性能达到了预期。SVR算法对数据的依赖较大,因此前期充分、有效的变量筛选和数据处理可保证最终模型的预测精度和泛化性能,本文在这2个方面做了大量工作,充分结合文献成果和实践经验,为模型的最终结果奠定了良好的基础。
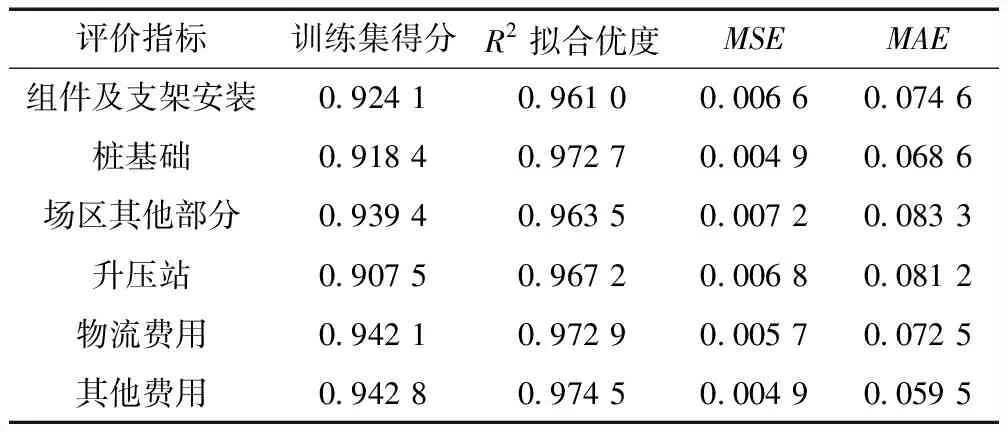
表5 模型结果评价
3 结 语
本文将海外光伏电站作为主要研究对象,将光伏电站总造价进行分解,得出6个需要预测的基本项,构建了基于向前向后逐步回归法的SVR模型预测海外光伏电站工程造价,得出以下结论:
(1)将光伏电站造价划分为组件及支架安装、桩基础、场区其他部分、升压站、物流费用和其他费用6个待预测部分,并通过专家访谈和调查问卷的形式得到各部分的影响因素,据此设计出模型的变量体系,为系统研究光伏电站各部分造价及总造价提供了思路,可为我国企业积极建设国内外光伏电站提供参考。
(2)将SVR算法和逐步回归法结合建立造价预测模型,模型预测精度较高。该模型融合了逐步回归法筛选显著变量的优势和SVR算法在小样本预测方面的优势,避免了传统预测方法的缺陷,为造价预测模型研究提供了新的思路。
