基于自适应提升随机森林算法的煤炭铁路发运量预测

郑海涛

（华北电力大学，北京 102206）

0 引言

2021 年出现了罕见的供电缺口。这是由于在全球供应链紧缺加上国内复工复产的环境下，中国外贸进出口贸易激增，工商业用电量均大幅增加，煤炭需求量激增。又叠加电厂季节性型增加库存，导致煤炭铁路出现运力不足，电厂存在煤炭短缺的情况。因此铁路发运量预测对稳定电力生产具有重要意义。

很多研究者对影响煤炭铁路发运量进行了分析。在经济环境方面，有研究者将铁路沿线的电厂发电用煤需求作为影响发运量的关键因素[1]，同时北方港口吞吐量对铁路运输也具有替代作用[2]。在运输成本方面，有研究者分别从铁路运价与煤炭联运的全程物流总成本[3]角度进行了煤炭铁路运输量的分析。

而在通过煤炭供需环境对煤炭铁路发运量进行预测几乎没有人研究，也几乎没有研究者将机器学习与数据挖掘方法加入对煤炭铁路发运量的预测当中。该文通过构建煤炭铁路发运量相关数据集，利用随机森林算法的高精度与决策可视化的优点构建煤炭铁路运输量预测模型，利用自适应提升法提高模型的精度与稳定性，利用模型找出与发运量相关的关键变量，并与其他传统算法进行精度与稳定性的对比分析。

1 煤炭铁路发运量相关数据集构建

在该研究中，利用大数据挖掘的思想，从煤炭的供需数据、运输价格、港口发运量和各环节煤炭库存等构建用于预测的煤炭铁路发运量相关数据集。

在煤炭供给方面，包括全国煤炭产量、各省煤炭产量、各种煤炭进口量、港口煤炭库存、全国煤矿库存和全国重点发电企业煤炭库存等。在煤炭的需求方面，包括全国二、三产业增加值与同比增长率、各省与全国的发电量、各省的火力发电量、各省的水力和风力发电量、各类型发电设备的装机容量、各地区的气温变动、各省的生铁产量以及各省的水泥产量等。在价格成本方面，包括了铁路运价、港口煤炭价格与山西煤炭现货价格。在运量方面，包括了各大港口煤炭吞吐量、太原局铁路发运量、大秦铁路发运量、朔黄铁路发运量以及合计铁路发运量等。

2 基于Ada-RF 的煤炭铁路发运量模型

该文将随机森林算法作为铁路发运量的底层预测算法对其进行回归分析。作为一个机器学习算法，和传统的线性回归模型和应对时间序列数据的自回归模型相比，随机森林算法有众多优点。除模型的精度与稳定性更高外，它可以通过模型内的损失函数与给输入变量设置权重的方法选取相关的变量进行回归或分类分析。和其他的黑箱模型相比，随机森林模型算法可以进行可视化，有一定的可解释性。随机森林是一种将多个决策树组合在一起的集成方法，通常用Bagging 或者pasting 方法训练[4]，和其他生成单一模型的算法相比，将多个模型整合的随机森林具有一定的先天优势。算法从原始样本中提取不同的多个样本，根据每个样本数据分别建立决策树模型，最终通过投票得到最终结果[5]。

随机森林回归模型是由多个决策树回归器组成的，每个决策树（CART）使用单个特征k、阈值与最小化成本函数将训练集分成2 个子集，成本函数如公式（1）所示。

式中：n为训练集中样本数量；nL、nR分别为特征分解阈值YkYk左、右两端样本数量。

公式（1）中，每个节点在分解子集时通过计算在利用k特征分解时阈值Yk左、右两端（或节点）的均方误差（MSEL与MSER）和最小【表意不明，请修改】，得到该节点最优特征k与最优阈值YkYk。通常情况下，在决策树模型做分类时会将基尼不纯度或信息熵作为成本函数中均方误差的替换项。

某节点的MSE 的结果是由该节点所有样本中变量y 的均值与每个y的实际值的差进行平方和计算得到的。

由于单一学习器导致误差较大，因此基于大数定理提高学习器的预测精度需要将多个弱分类器结合成一个强分类器，即将多个决策树模型结合为一个模型（随机森林模型）。其中结合多个模型的方法为Bagging 算法。Bagging 的基本流程是采样出M个含有n个训练样本的采样集，然后基于每个采样集训练出一个CART 学习器，再将这些CART 学习器进行结合。对预测输出进行结合时，Bagging 对回归任务使用简单平均法。

为了进一步提高模型的预测精度，该研究选用自适应提升法对随机森林算法进行模型精度与稳定性的提升。随机森林模型对训练集预测后，在每个样本上都会产生一个不同预测误差，AdaBoost 算法[6]会为每个样本重新设置权重，针对预测误差较高的样本模型，在下一次的迭代中，算法会针对这一部分的样本模型进行进一步的优化提升。它使用更新后的权重训练第二个随机森林学习器，并再次对训练集进行预测和更新权重，直到训练出较为合适数量（N）的随机森林学习器[7]。AdaBoost 使用权重aj对它们进行加权，最后得到的大多数加权投票的预测结果就是最终模型给出的预测结果，如公式（3）所示。

式中：M为学习器数量；k为第j个学习器的预测值。

这在一定程度上解决了一般模型容易发生过拟合的问题。由于数据样本量较少，同时为了提高模型的精准度与稳定性，避免过拟合，因此需要在模型训练过程中降低决策树的自由度，即对模型中n_estimators（决策树数量）、max_depth（决策树深度）等超参数进行正则化。

利用网格搜索最终确定该模型的超参数。网格搜索是对每个超参数选择一个较小的有限集去探索，这些超参数笛卡尔乘积得到若干组超参数，然后网格搜索使用每组超参数训练模型，挑选验证集误差最小的超参数作为最好的超参数。

模型构建流程图如图1 所示。

图1 Ada-RF 模型构建技术路线图

该研究分别对太原局铁路发运量、大秦铁路发运量、朔黄铁路发运量和合计铁路发运量4 个变量构建模型，利用网格搜索分别对这4 个模型寻找超参数，最终确定的超参数见表1。

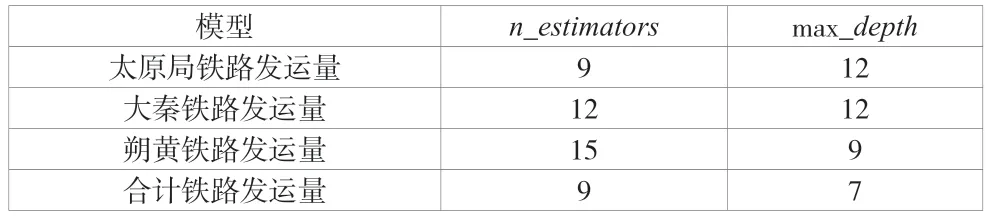
表1 模型超参数设置表

3 模型预测结果对比分析

为验证模型的预测精度，分别构建自适应提升的随机森林模型、随机森林模型（RF）、自适应提升的决策树模型（Ada-Tree）、线性回归模型（LR）与决策树模型（Tree）分别对太原局铁路发运量、大秦铁路发运量、朔黄铁路发运量与合计铁路发运量进行预测。为客观评估各预测模型的精度与稳定性，该研究选择平均绝对误差（Mean Absolute Error，简称MAE）验证模型的精度，用均方误差（Mean Square Error，简称MSE）验证模型的平稳性，计算公式如公式（4）、公式（5）所示。

式中：n 为样本数量；为样本i 中被铁路发运量真实值；为样本i 中被铁路发运量预测值。

使用5 折交叉验证方法验证各模型预测精度，结果见表2。

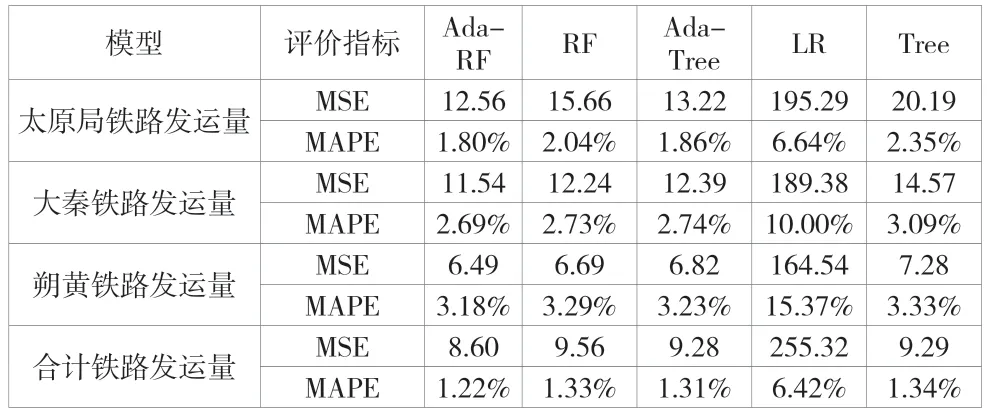
表2 模型预测精度与稳定性表

从表2 可以看出，Ada-RF 模型对各铁路线发运量预测误差均在3.2%以下，其中对太原、大秦、朔黄的合计铁路发运量的预测效果最好，预测精度达到98.78%，预测结果的均方误差为8.60。其次为对太原局铁路发运量的预测，预测精度达到98.20%，预测结果的均方误差为12.56。同时Adaboost提升法对随机森林模型精度的提升在1.25%至11.92%。相比之下，Ada-RF 在预测精度与稳定性上均强于其他模型，尤其是比传统线性回归模型的预测精度平均提升了7.39%。从总样本中随机选取90%的样本作为训练集，其余样本作为测试集，利用上述各模型合计三大铁路煤炭发运量，结果如图2 所示。除线性回归模型外，其余机器学习模型对铁路煤炭发运量的预测效果都是较为理想的，Ada-RF 模型的回归预测效果最好，最贴近真实值。

图2 各模型预测效果图

机器学习算法可以通过模型内置函数得到不同变量的重要程度，这样对模型的拟合得到影响铁路月煤炭发运量的关键性因素，利用大数据挖掘的思想，从众多的相关变量中筛选出影响其变动的实际的关键因素，太原局铁路发运量、大秦铁路发运量、朔黄铁路发运量与合计铁路发运量的重要程度排序见表3。

由表3 可以看出，影响太原局铁路发运量的关键因素包括各地区的发电量、水力发电占比与进港煤炭量等。影响大秦铁路发运量的关键因素包括港口库存量、出港煤炭量、火电发电量量同比增长率与秦皇岛港口煤炭价格等。朔黄铁路发运量主要和各地区发电、港口煤炭的库存及港口进出量相关。而合计铁路发运量除了同样受港口情况影响外，还有工业同比月增长率、山西电煤价格、全国重点电厂库存等影响因素。

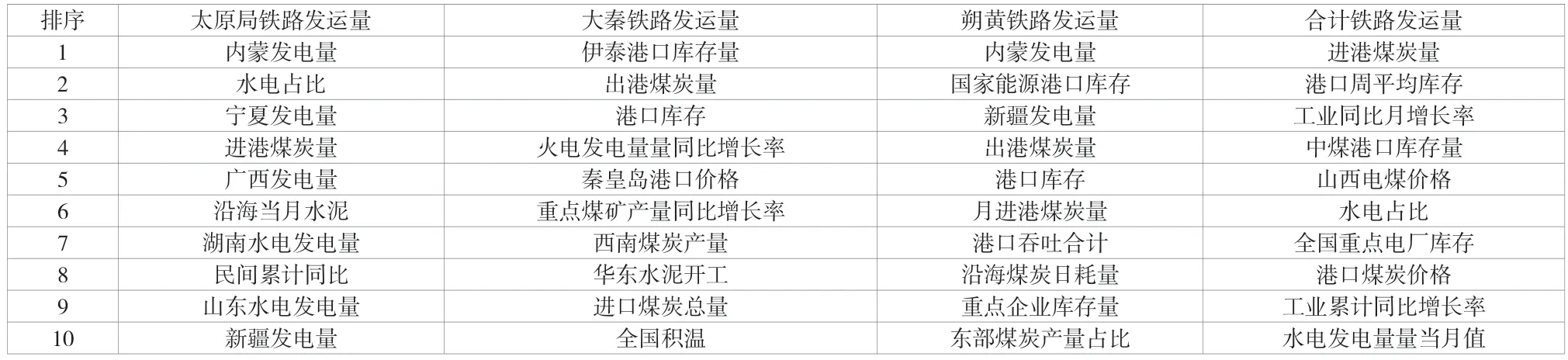
表3 影响煤炭铁路发运量的关键影响因素

4 结语

该文通过煤炭铁路发运量相关的月度数据进行数据集构建。影响煤炭铁路发运量的影响因素较多，为提升铁路发运量的预测精度，寻找影响煤炭铁路发运量的关键影响因素，该研究中构建了自适应提升的随机森林算法预测模型，该方法对影响因素较为复杂的煤炭铁路发运量的预测精度较高。先将构建的数据集训练随机森林模型，利用网格搜索找到最优超参数，然后利用自适应提升法对随机森林模型进行迭代提升，得到最终的煤炭发运量预测模型。利用该方法分别对太原局铁路发运量、大秦铁路发运量、朔黄铁路发运量与合计铁路发运量进行预测，同时选取了多种模型与2 种模型误差评价指标，验证了模型预测的精度与稳定性，同时根据模型赋予各变量的重要性确定了影响煤炭铁路发运量的关键影响因素。结果发现，使用Ada-RF 模型对铁路发运量的预测精度与稳定性都优于其他模型，同时自适应提升对煤炭铁路发运量预测模型的预测效果有明显提升。该研究对铁路发运量影响因素发掘、煤炭供应链的稳定和火电厂安全生产具有一定意义。