基于LBM的发射装置阀口结构多目标优化

戴德志,姜永正,马俊飞,叶小兵

(1.湖南科技大学 机械设备健康维护湖南省重点实验室,湖南 湘潭 411201;2.湖南省云箭集团有限公司,湖南 长沙 410100)

现代战争中适应于复杂城市环境作战的小型智能弹药(如巡飞弹、旋翼式弹药等)出现在战场上,一般针对该类弹药的发射方式有液气压弹射式、电磁弹射式、弹力弹射式以及燃气弹射式等[1],其中燃气弹射式因其反应速度快且出筒速度有保障被国内外广泛应用到各类智能弹药的发射系统中。

对于燃气弹射式的发射方式,有效控制弹药出筒速度以及在发射过程中的最大负载以保证发射过程稳定可靠十分重要[2]。裴胤等[3]构建了一类火箭炮动力学仿真模型,针对火箭弹在管内的运动及受力情况进行了研究,得到了该火箭炮发射运行时各部件的运动及负载情况。邬欣明[4]使用虚拟样机与仿真手段,对某类车载自动迫击炮展开仿真研究,理清了该迫击炮的射击稳定性。陈世业[5]建立了自行火炮弹炮多体发射动力学模型,模拟了完整的火炮发射过程,分析了各结构参数对弹药在筒内运动状态的影响。赵坚等[6]对产气药柱展开了一维、二维及三维的一体化计算,得到了双燃速内弹道性能和流场中燃气参数的分布。周哲等[7]针对推进剂燃烧及对内弹道的影响展开研究,对不同药柱数和点火药药量所能提供的负载-时间的变化响应关系进行了研究。王立新等[8]从底火药燃烧能量释放的角度切入,研究不同初温条件下底火的能量释放特性,揭示了底火初温对发射装置能量释放的影响。鲍文等[9]研究了一种气动式燃气流量调节阀,通过仿真得到了燃气发生器及其调节阀的动态响应特性。国外针对弹射装置的燃气流量调节方面也开展了诸多工作,包括燃气流量调节阀的设计、试验和燃气流量调节系统控制器研究。DUNAWAY等[10]设计了一种膨胀室位于高压室外侧的燃气发生器,两个室之间以通孔连接,以此防止低压室内出现过高的压强,提高发射装置的安全性与稳定性。王鸿丽等[11]建立内置式发射动力系统发射过程仿真模型,利用该模型得到了弹药发射出筒过程中的能量利用系数。

在前人的研究基础上,本文提出一种阀口优化方法,在对出筒速度有不同需求时,可快速选取对应该出筒速度要求的最佳阀口结构参数。通过仿真试验,得到出筒速度及弹药峰值负载对进口倾角、出口倾角、通孔面积及通孔长度的响应关系。通过正交试验设计分析,得到数据拟合响应模型。根据不同出筒速度的前置需求,由所得曲线模型选取弹药所受峰值负载最小时的阀口结构参数。在此优选的阀口的影响下,降低发射筒内部的压强,保障出筒速度,减小发射时弹药所受峰值负载,保证智能弹药发射过程的稳定可靠。

1 基本结构

为了确保该类智能弹药发射装置的安全性与可靠性,需要对火药燃烧后产生的燃气释放进行控制,以保证在发射过程中一方面满足弹药出筒后的速度需求,另一方面满足智能弹药对所承受峰值负载大小的限制。

该弹射装置由底火装置、弹药、发射筒三大部分组成。在底火装置内,点火药在经过电子点火控制系统引燃后进一步点燃底火药,底火药燃烧产生高压燃气经过阀口进入低压室即发射筒内,推动隔热活塞运动,进一步将弹射力传递给智能弹药。过程中因为阀口与活塞的存在,智能弹药在发射过程中所受负载得以控制,隔绝了高温燃气。其结构如图1所示。

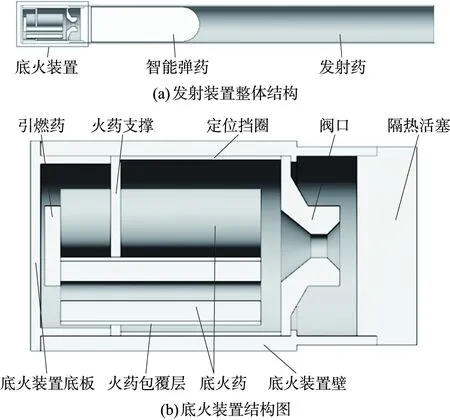
图1 发射装置结构Fig.1 Launcher structure

2 数学模型

2.1 基本假设

忽略发射过程中所产生的固体颗粒对整个发射过程的影响。简化发射系统,火药燃烧过程用质量入口代替,简化活塞与智能弹药,简化阀口外轮廓设计。默认火药燃烧过程产生的为可压缩的理想气体,满足理想气体方程。

2.2 数学模型

火药燃烧过程是本装置在发射过程中非常重要的一个过程,因火药实际燃烧的过程十分复杂且多变,因此对火药燃烧过程给出以下假设：

①火药燃烧为端面燃烧,药柱燃烧的面积保持不变;

②燃气为纯气体,无固体颗粒;

③燃气的温度保持不变,对压力影响不考虑;

④燃气服从理想气体状态方程。

根据火药的几何燃烧定律可以导出燃气生成速率[12]。设mp为装药初始质量,V为装药单体的已燃去体积,V0为装药单体的原有体积,np为装药单体的数目,ρp为装药密度。令Ψ=mb/mp为装药已经燃去的质量与装药初始的质量比,因为mp=npρpV0,mb=npρpV,故：

(1)

Ψ也为装药单体燃去部分的体积与装药单体初始体积之比,简称装药燃去百分比。

将Ψ对时间t微分得：

(2)

假设某时刻装药的表面积为Sb,在dt时间内燃去的厚度为de,则：

dV=Sbde

(3)

式中：u为火药的线性燃烧速度,简称燃速。

(4)

装药的燃气生成速率,即每秒燃气生成量,其表达式为

(5)

在实际使用中,在弹射器高压室工作压强范围内,一般均采取指数式计算燃速,即：

u=apn

(6)

式中：a为燃速系数,n为燃速压强指数,pn为纲量为1的量。

3 数值计算方法

3.1 格子玻尔兹曼方法

格子玻尔兹曼方法(Lattice Boltzmann method,LBM)是一种新兴的流体系统模拟方法,其具有宏观流体连续模型和微观分子动力学方法的优点,现已被广泛用于多相流、气固两相流及内部流等[13-15]。

LBM基于非平衡统计物理学的基本方程——玻尔兹曼方程。本文采用LBM方程模型描述流体粒子在具有一定的离散速度的情况下其分布函数在固定的方格上的运动过程。LBM中粒子演化规则包括移动和碰撞两个过程,演化方程如下[16]。

移动：

(7)

碰撞：

(8)

3.2 边界条件

为简化仿真,对该弹射器的整体结构进行简化后导入模型到xflow中,其简化后的几何结构截面如图2所示,其中发射筒由阀口将其划分为高压室与低压室。

①环境设置。整个发射系统垂直发射,受重力作用,气体介质设为空气,采用单向内部流模型,初始条件设重力加速度为9.81 m/s,环境温度为288.15 K,空气密度为1.225 kg/m3。

②质量入口边界。取单根药柱质量流量入口,根据所得的火药燃烧时燃气生成规律,设置入口为质量流量入口。因为该发射装置发射时内部压强较小,故压强对该类黑火药的燃速受压强影响较弱,且本文的研究目标在于阀口的结构对发射筒内压强的影响与控制,故取10 g的火药量,其质量流入为0.01+2t,t为底火药燃烧时间。所选火药的密度为1.80 g/cm3,火药燃速为8～10 mm/s,火焰传播速度1 000～3 000 mm/s。

③刚体动力学。简化后的智能弹药与隔热活塞用一个圆柱代替,其密度为78 000 kg/m3、质量为15.1 kg、动摩擦系数设为0.25。考虑到其在出筒过程中受到的摩擦力与空气阻力,因此对该圆柱设置一个竖直向下的外部力F=45 N。

④边界设置。考虑到数值出口与实际出口的偏差,设置数值出口尽量远离实际出口,以此来减小误差,外部流体域的下部设置为压力出口,其他边界均使用wall边界。

⑤格子划分。格子划分采用八叉树式结构,对于阀口处的格子进行细化处理。边界条件设置及格子划分如图3所示。

图3 格子划分以及边界条件设置Fig.3 Grid division and boundary condition setting

3.3 动力学模型有效性验证

基于已有实验数据及结果,对该动力学模型的有效性进行验证,所得结果与实验结果进行对比。实验及仿真计算结果如表1所示。对比实验结果和仿真结果可见,在仿真初始条件参数与实验初始条件参数相同时,二者结果相差较小。因此,可验证该仿真模型的有效性。

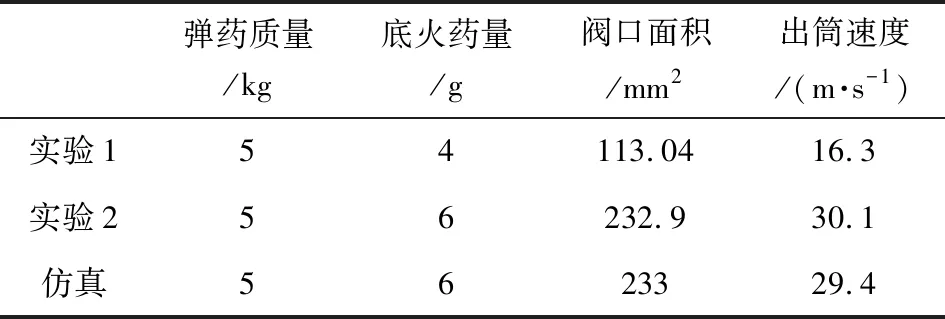
表1 仿真结果与实验结果对比Table 1 Comparison between simulation results and experimental results

4 结构参数对发射性能的影响

4.1 正交试验设计

对阀口的结构参数进行调整,分析调整后的进口倾角、出口倾角、通孔长度以及通孔面积对出筒速度和弹药峰值负载的影响,找到主要影响因素,拟合因素与响应之间的模型曲线,得出最佳的设计方案。结构参数如图4所示。

图4 结构参数示意图Fig.4 Schematic diagram of structural parameters

以阀口进口倾角、出口倾角、通孔长度以及通孔面积为变量设计正交仿真试验,以出筒速度以及过程中所受峰值负载为评价指标,仿真结果如表2所示。表中,α为进口角度,β为出口角度,L为通孔长度,S为通孔面积,v为出筒速度,F为发射峰值负载。

表2 正交仿真试验结果Table 2 Results of orthogonal simulation test

4.2 出筒速度与发射峰值负载随单一结构参量的变化规律

基于表2的数据,对变量和连续响应之间的关系进行拟合建模,得出弹射器发射过程的出筒速度以及弹药峰值负载和阀口的进口倾角、出口倾角、通孔长度、通孔面积之间的关系,如图5和图6所示。

图5 弹药出筒速度随单一阀口结构参数的变化规律Fig.5 Change rule of ammunition exit velocity with structural parameters of single valve port

图6 峰值负载随单一阀口结构参数的变化规律Fig.6 Change rule of emission load with structural parameters of single valve port

由图5可知,当进口倾角在20°～30°的范围时,曲线斜率较小,该范围内的倾角变化对出筒速度影响较小,当进口倾角在30°～65°的范围时,随着进口倾角的增大,智能弹药的出筒速度呈下降趋势,进口倾角的改变对弹药出筒速度的影响差值为0.27 m/s;出口倾角在20°～30°的范围变化时,对应曲线段的斜率接近0,而后出口倾角在30°～65°的范围时,弹药出筒速度与出口倾角成反比,弹药出筒速度的变动差值为0.56 m/s;通孔长度在10～30 mm范围变化时,弹药出筒速度随之减小,其变化值为1.32 m/s;通孔面积在150～260 mm2时,弹药出筒速度随着通孔面积的增大而增大,通孔面积对出筒速度的响应值为2.55 m/s,通孔面积在260～350 mm2范围内时,出筒速度随着通孔面积增大而减小,通孔面积对出筒速度的响应值为1.83 m/s。

由图6可知,当进口倾角在20°～42°范围内变化时,峰值负载有小幅度的增长,增幅值为304 N,进口倾角在42°～65°变化时,峰值负载有小幅度减小,变化值为283 N;出口倾角在20°～38°范围内变化时,峰值负载小幅度增大,其增值为190;当出口倾角在38°～65°范围内变化时,峰值负载随着出口倾角增大而减小,减小幅值为414 N;通孔长度在10～30 mm范围内逐渐增大时,峰值负载与其成反比,峰值负载由7 654 N递减到6 796 N,减小幅值为858 N;通孔面积在150～260 mm2范围内时,峰值负载随通孔面积的增大而增大,该范围内通孔面积对峰值负载的响应值为1 368 N,在通孔面积于260～350 mm2变化时,峰值负载随之减小,减小幅值为986 N。

综合图5和图6可知,通孔长度与通孔面积对弹药出筒速度以及峰值负载影响较大,其主要原因是通孔的长度增加,导致燃气气流通过孔隙时,其所损失的动能更大,导致出筒速度减小;同时,通孔长度的增加也使得流入低压室的燃气更加平稳,减小了隔热活塞的负载冲击。通孔面积的增加使得更多的气体可以更加迅速地由高压室流入到低压室,且因增大孔径后,燃气流速减小,不会对隔热活塞产生大量冲击,动能损失较少。因此,随着通孔面积的增大,出筒速度以及峰值负载都会有明显的增加。通孔面积增加到一定程度,使得气流流进阀口时,流量增大,流速减小,气流不会高速射出冲击活塞,活塞所受负载减小,这导致出筒速度以及峰值负载减小。出口倾角与入口倾角对出筒速度以及峰值负载的影响不明显,主要是因为整个发射装置内部的气体压力都较高,导致倾角的改变对整体影响不显著;另一方面,进出倾角的斜边长度较短,其对燃气气体的流动状态影响较微弱。

5 阀口结构参数优选优化

5.1 物理参数优选优化

根据该类智能弹药发射的基本性能需求,需要满足其发射后的出筒速度要达到22 m/s以上为最佳,因此在该前提下,应尽量减小其发射过程中所受峰值负载。故根据图5和图6可确定,对于通孔长度,当速度v≥22 m/s时,通孔长度L≤27.5 mm,继而分析可知,满足通孔长度L≤27.5 mm时,L取27.5 mm,峰值负载最小;同理通孔面积取170 mm2≤S≤345 mm2时,可满足v≥22 m/s,进而考虑到峰值负载需尽量小,由图6(b)可知,S=170 mm2,对于进口倾角与出口倾角,因其对出筒速度以及峰值负载影响小,故二者与改进前的倾角取相同值,即α=β=45°。对上述所选结构参数的阀口进行仿真验证,并与优化前的结果进行对比。

5.2 优化前后结果对比分析

优化前后的位移与速度曲线分别如图7和图8所示。优化前后弹药负载和高低压室压力曲线分别如图9和图10所示。

图7 优化前后位移曲线Fig.7 Displacement curve before and after optimization

图8 优化前后速度曲线Fig.8 Speed curve before and after optimization

对比优化前后的位移与速度曲线可知，优化后弹药出筒所用总时间较长,因此其在发射筒内经历了更长的加速时间,也因此获得了更大的出筒速度。从图8及图9可以看到：开始阶段为0～0.04 s,优化前的速度曲线斜率相比优化后的速度曲线斜率大,对比图10可发现,这是因为此阶段弹药所受载荷较大,其获得较大的加速度,虽然弹药在出筒时的速度会增加,但同时弹药在筒内运动时所受负载也增加了。经过优化后,该阶段的弹药负载变小,加速过程也更加平稳,速度相对降低。中间阶段为0.04～0.06 s,在该阶段优化后的发射装置弹药所受负载较优化前较大,相较于优化前其负载平稳,因此其速度在此阶段大幅提升,保障了最后出筒时刻的速度需求。出筒阶段为0.06～0.093 7 s,该阶段优化后的发射装置依然处于一个平稳的加速过程,加速至0.093 7 s完成出筒,而优化前出筒时刻为0.084 3 s。虽然优化后负载的减小导致其加度也减小,但是优化后智能弹药在筒内的运行时间变长,进而有效地提升了加速时间,避免了出筒速度因负载减小而出现同步减小的情况。

图9 优化前后弹药负载曲线Fig.9 Load curve of ammunition before and after optimization

图10 优化前后高低压室压力曲线Fig.10 Pressure curve of high and low pressure chamber before and after optimization

由图9可知,在发射过程中,优化后的阀口结构使发射时弹药所受负载峰值明显下降。峰值出现后,活塞的运动导致低压室体积变大,这使得高压室与低压室的压强与活塞受负载均变小;而后,曲线再次上升,并且优化后的F-t曲线在二次峰值之后的走势趋于平稳,这也对应图8中速度曲线的走势,得以相互验证。同时,优化后负载峰值出现的时间提前,使得底火药所产生的燃气相应减少,进而减小了整个发射装置内部压强与弹药所受负载。由图10可知,优化前后压强的最大峰值曲线走势与图9中弹药所受负载曲线相互呼应、相互验证。在该压强曲线中,优化前发射筒内部高压室与低压室的压强均超过1 MPa,过大的压强对于该发射装置的安全性提出了挑战,并且优化前其低压室内部压强相较高压室内部压强阀口减压效果不明显,优化后高压室压力曲线均可控制在1 MPa以下,而其低压室压强曲线均在0.8 MPa之下,并且对比优化后的高压室与低压室的压强曲线可以明显发现,优化后的阀口减压明显有效。

图11为优化前后峰值负载时刻的阀口处总压力云图。由图可见,优化后的阀口处压强在峰值负载时刻相较于优化前减小了18.9%,同时结合速度矢量图12可见优化后通孔长度的增加以及阀口面积的缩小使得高压气体流经通孔时流速增加,进而转换为动能消耗,减小了对活塞的冲击载荷。优化后的阀口使得气流流出时更多气流可沿锥形面流向周边,减小了气流对活塞中部的直接冲击。

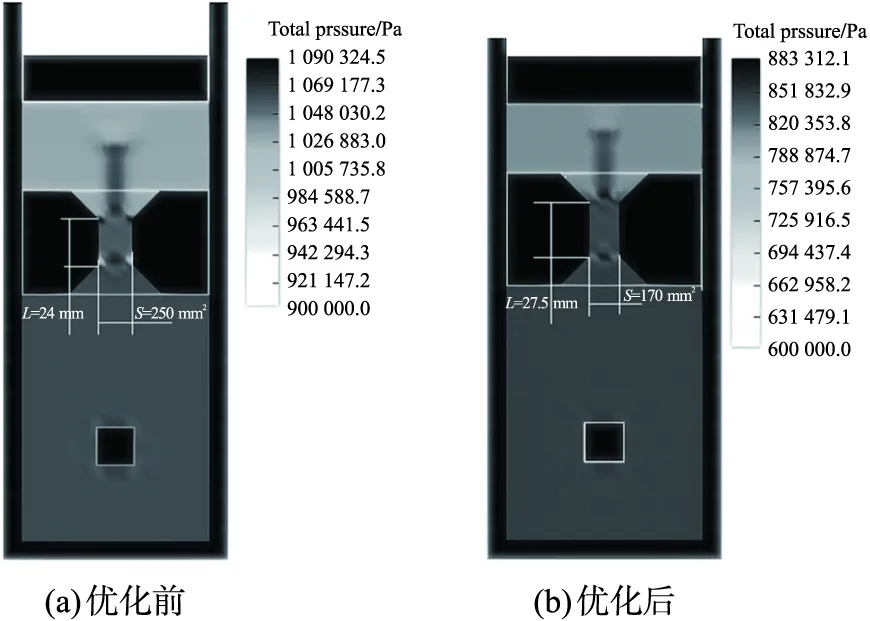
图11 优化前后最大载荷时刻发射筒内部压力云图Fig.11 Internal pressure nephogram of launcher at maximum load before and after optimization

图12 优化前后最大载荷时发射筒内部速度矢量图Fig.12 Internal velocity vector diagram of launcher under maximum load before and after optimization

优化后的发射装置对比改进前,一方面其出筒速度相差2.35 m/s,减小了9.49%;另一方面,优化前后的峰值负载减小了1 623 N,降低了20.15%。优化前后,高压室最大压强减小了0.114 MPa,相对优化前降低9.8%,低压室最大压强减小0.220 3 MPa,相对降低21.42%,峰值负载峰值出现时间提前了0.003 1 s。具体对比数据见表3。优化后的负载曲线更加平稳,第二次波峰的幅值较小,并且低压室的压强减小更加明显。在出筒速度减小9.49%的基础上,总体发射性能有较大提高,峰值负载降低了20.15%。因此,通过该优化方案,实现了在小幅度降低智能弹药出筒速度的前提下,大幅减小智能弹药所受负载,增强发射稳定性的目的,该优化方法具有较高的可行性。

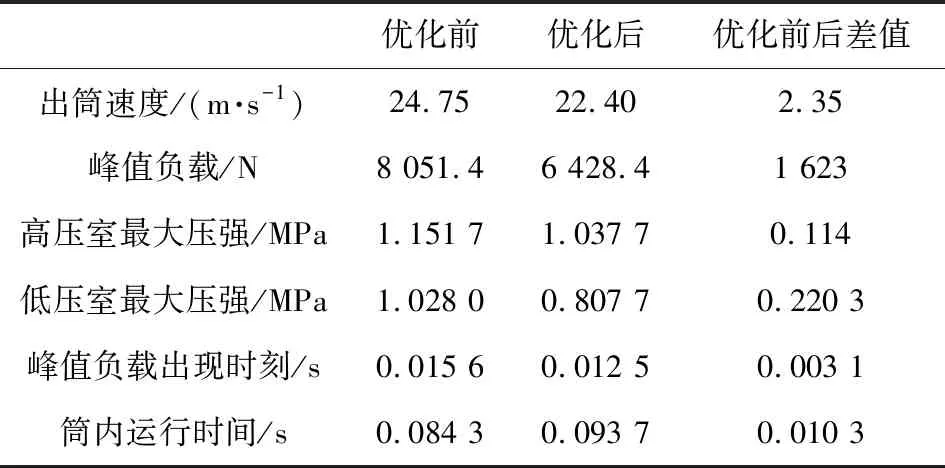
表3 优化前后发射装置各性能参数对比Table 3 Comparison of various performance parameters of launcher before and after optimization

6 结束语

影响发射装置发射性能的因素颇多,从阀口结构参数的优化角度出发是一种便捷、快速的方式。本文以一种智能弹药发射装置为研究对象,分析了该发射装置阀口的进口角度、出口角度、通孔长度以及通孔面积对弹药出筒速度以及峰值负载的影响,对阀口结构进行优化,得出以下结论：增加通孔面积与通孔长度,虽然发射装置发射的弹药出筒速度会小幅减小,但是可明显且有效地降低峰值负载,提升发射装置性能。

在本文的研究范围之内,通过对阀口的进口倾角、出口倾角、通孔面积以及通孔长度对弹药峰值负载及出筒速度的影响进行拟合分析后,可实现根据所需的不同出筒速度选取合适的阀口优化结构参数,使得发射过程中发射筒内部压强以及弹药所受峰值负载达到一个较低值,且出筒速度有所保障。

通过该优选优化方法,对比优化前后的阀口作用下的发射情况,优化前后弹药出筒速度相差2.35 m/s,峰值负载减小了1 623 N,对比优化前后,高压室最大压强减小了0.114 MPa,低压室最大压强减小0.220 3 MPa。弹药发射过程中所受峰值负载减小了20.15%,低压室最大压强减小了21.42%。由此可见,该阀口优化方法可以显著降低弹药发射过程中所受峰值负载,减小发射筒内部压强,实现根据不同出口速度的要求选择不同结构参数的阀口,并减小弹药所受峰值负载的目的。