雷达杂波高精度模拟技术研究
2023-04-06王旭旸高希权楚学胜
王旭旸,李 闯,胡 斌,高希权,楚学胜
(北京无线电计量测试研究所,北京100039)
1 引言
雷达利用电磁波的散射特性,可用于探测与识别目标。然而,目标周围的自然环境中会对雷达发射的电磁波产生散射,从而对目标信号的检测产生干扰,这些干扰称为杂波。作为一种不期望的雷达回波,杂波对雷达性能往往会产生较大影响。
因此,现代雷达技术的一个重要方向就是通过相应信号处理技术,尽可能获得高精度、远距离、高分辨率和多目标信息,最大限度降低杂波的干扰[1]。
通过外场实验测试杂波数据存在着经济成本高、实时存储分析资源大等缺点,因此雷达杂波模拟的研究具备重要的理论和工程意义。雷达系统的发展对于雷达信号的带宽和实时性有较高要求,高带宽雷达目标系统具有很高的距离分辨率,需要采用多散射点模型,结合雷达的速度、距离、方位与杂波表面的散射特性,进行高精度模拟[2]。
设计了一种雷达杂波高精度模拟方法,可以实现64 个散射点×4 096 个数据单元的雷达杂波高精度模拟。该模拟方法主要包括雷达杂波的建模与仿真以及数字射频存储(DRFM)的具体实现两部分。通过介绍如何产生杂波数据以及将杂波数据与基带数据进行数字正交调制的相关方法,为后续杂波模拟器的硬件实现提供了理论支撑,具有较高的工程应用价值。
2 雷达杂波的建模与仿真
介绍一种基于Matlab 的雷达杂波建模与仿真方法,旨在生成不同类型的杂波序列,并将其储存在FPGA 的RAM 中。通过外部选择指令,该方案能输出相应杂波序列,并针对不同场景实时变化参数,实现动态模拟。
2.1 散射单元划分
为实现杂波的精细化模拟,需要对较大区域实现精细化划分。根据雷达导引头到地面的距离不同,将杂波整体区域划分为多个等距离环[3]。对于每个距离环内部的杂波,采用统计特性建模方法进行模拟。雷达分辨单元的散射体具有随机分布特性,因此雷达散射机理可以视为随机过程。通过研究杂波的幅度分布特性和功率谱特性,即可建立杂波的统计模型,再通过零记忆非线性变换法(Zero Memory Nonlinearity,ZMNL)或球不变随机过程法(Spherically Invariant Random Process,SIRP)产生一组能满足杂波统计特性规律的时域随机信号,实现对杂波的模拟仿真[4]。最后,可以根据相关要求调整杂波参数,验证其特性。整体流程如图1所示。
为了实现高精度的雷达杂波模拟,需要对较大的回波照射区域实现精细化划分。回波区域通常具有较大的面积,不同位置的散射特性有一定差异。根据雷达导引头到地面的距离不同,通过控制延时时间,将整个杂波区域划分为多个等距离的环,其中每个环视为一个散射点。在区域面积固定的情况下,圆环划分越精细,散射点数越多,模拟精度也越高[5]。当模拟精度较高时,可视为散射点圆环内部每个点到雷达的距离相等。在散射点内部可以进一步划分出具有相同散射特性的散射单元。每个散射点之间具有不同的延时和幅相信息,彼此可以作为独立目标刻画模型。等距离环示意如图2所示。
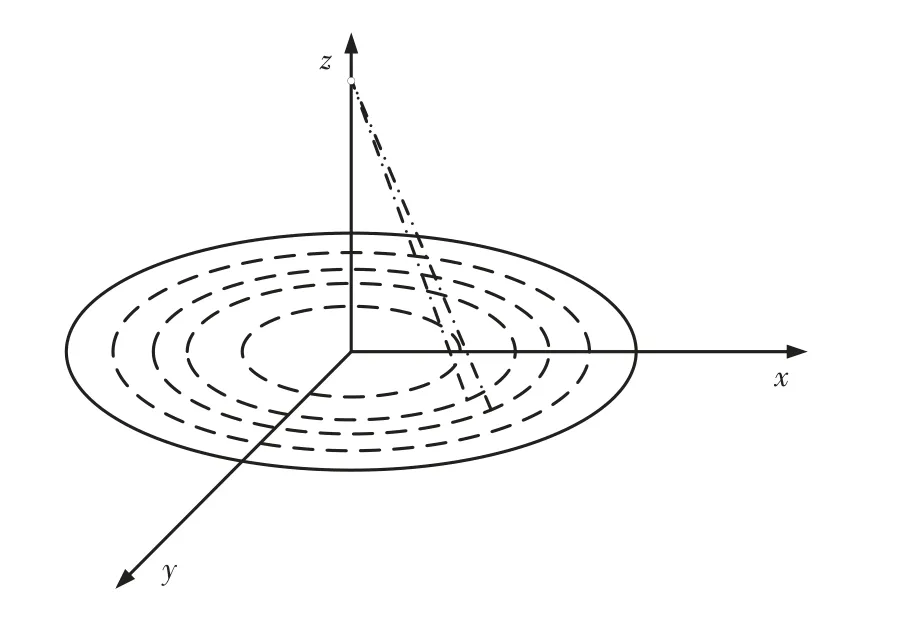
图2 划分等距离环示意图Fig.2 Schematic diagram of dividing equidistant rings
2.2 杂波的建模方法
杂波的幅度分布具有随机起伏特性,早在1951年,Goldstein 便首次提出了将统计模型应用于海杂波描述的想法。常用的幅度分布统计模型有瑞利(Rayleigh)分布、对数正态(Log-Normal)分布和韦布尔(Weibull)分布[6]。
Rayleigh 分布的概率密度函数为:
式中:δ——雷达杂波的均方根。
均方根取值不同时,Rayleigh 分布情况不同。通过Matlab 绘制了其概率密度分布图,如图3所示。
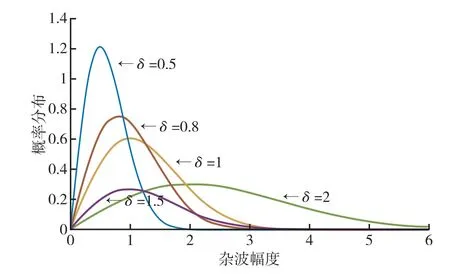
图3 瑞利分布概率密度图Fig.3 Plot of the Rayleigh distribution probability density
Log-Normal 分布的概率密度函数为:
式中:μ——分布的均值;δ——分布的偏斜度。
Log-Normal 分布的右拖尾高度随δ的增加而提升。Weibull 分布具有更强的适应性,适合模拟幅度起伏较为均匀的地海杂波。Weibull 分布的概率密度函数为:
式中:p——分布的偏斜度;q——分布的均值。
分布均值q不变时,Weibull 杂波的右拖尾高度随着偏斜度p的提升而减小[7]。
来自同一区域回波的杂波信号之间具有时域相关性,通常用功率谱特性来描述。通常采用高斯模型、柯西模型、立方模型和指数型模型等模型来描述杂波功率谱特性。
2.3 杂波的仿真方法分析
杂波的仿真过程就是通过零记忆非线性变换法或球不变随机过程法产生一组能满足杂波统计特性规律的时域随机信号[8]。两种方法的优缺点对比如表1所示。
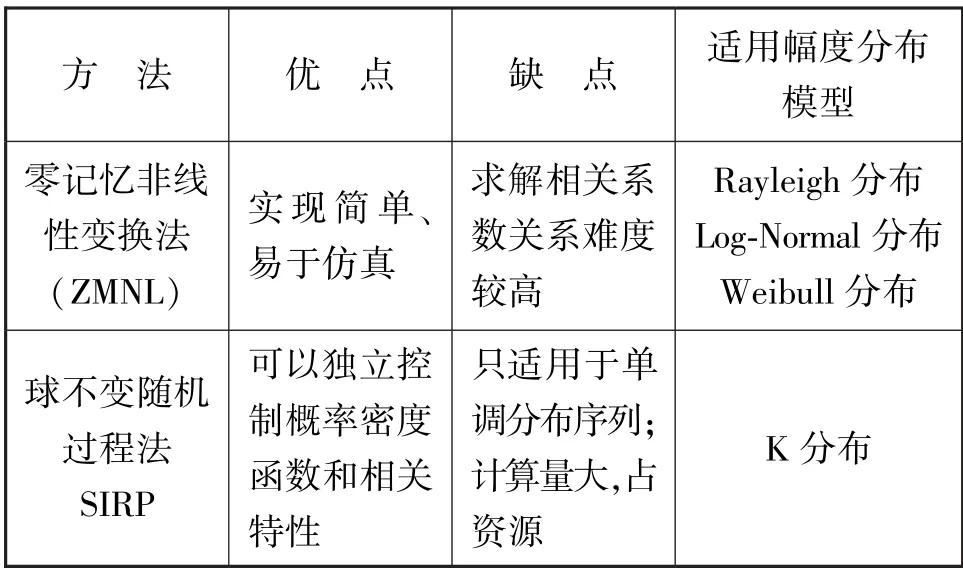
表1 常用杂波仿真方法对比Tab.1 Comparison of common clutter simulation methods
ZMNL 方法原理图如图4所示。
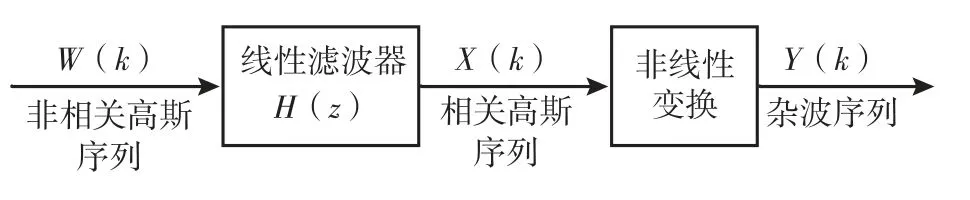
图4 零记忆非线性变换法原理图Fig.4 Schematic diagram of zero memory nonlinearity
其基本原理是由已知的高斯白噪声信号W(k),通过一个具有杂波功率谱特性的有限长单位冲激响应(Finite Impulse Response,FIR)数字滤波器H(z)获得相关高斯随机过程序列X(k),再利用X(k)通过零记忆非线性变换方法来得到相关随机过程序列Y(k),Y(k)即为所求杂波序列。
使用ZMNL 方法实现Log-Normal 分布的流程如图5所示。
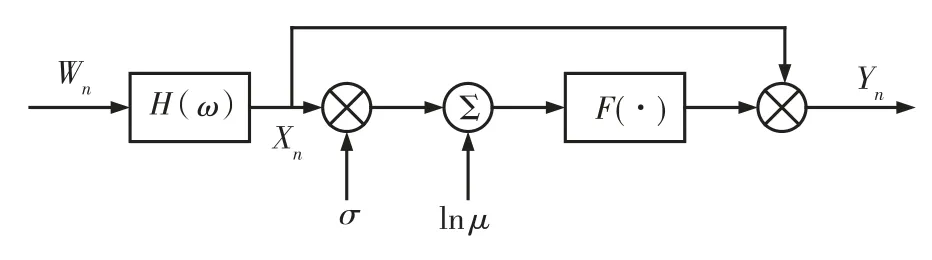
图5 ZMNL 方法实现Log-Normal 分布流程图Fig.5 Flow chart of ZMNL method to realize Log-Normal distribution
从图5 中,可知:
式中:erf(x)——误差函数。
Log-Normal 分布杂波Matlab 仿真结果如图6所示。通过观察可知,仿真产生的杂波各项指标与理论值十分接近,该仿真方法产生的杂波可以用于后续计算。
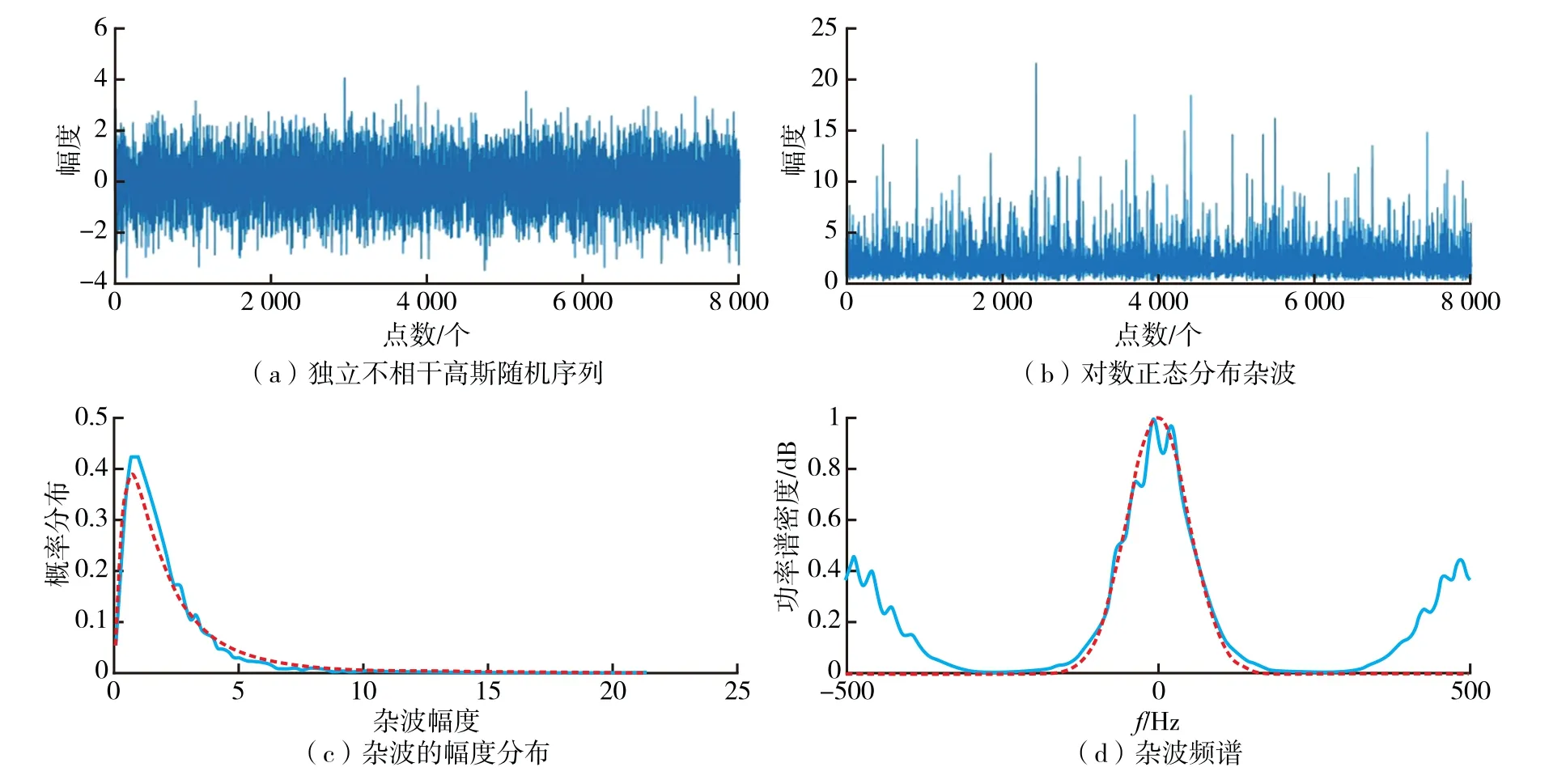
图6 Log-Normal 分布的仿真结果图Fig.6 Simulation results graph of Log-Normal distribution
3 杂波模拟结构设计
杂波数据通过Matlab 模拟仿真,经过IFFT 变换和加窗搭接后存入FPGA 的RAM 中。为实现信号处理中的速率匹配,使用多级CIC 滤波器和FIR滤波器提升采样频率。将杂波信号进行幅度加权,分为I、Q 两路信号后备用。基带回波信号经过ADC 采集后,通过数字下变频的方式实现零中频,经过FIR 滤波器和FIFO 延时后,最终产生I、Q信号。
将产生的杂波信号采用数字正交调制方式调制到基带信号上。合理复用上述模块,将不同延时量的基带信号与杂波信号进行调制,可以实现64个散射点的高精度杂波模拟[10]。最后,通过数字上变频信号将调制后的信号恢复成中频信号,并通过DAC 完成输出。全过程流程如图7所示。

图7 杂波模拟结构设计图Fig.7 Structure design of clutter simulation
3.1 杂波数据的处理
对频谱进行观察时,通过频域窗函数看到的频率的宽度称为频率分辨率。频率分辨率数值越小,分辨率就越好[11]。
频率分辨率f0满足如下关系:
式中:fs——杂波信号的采样频率;N——采样点数。
采样频率不变的情况下,采样点数越多,频率分辨率越小,模拟的精细程度也就越高。因此,在Matlab 模拟产生杂波数据时,将传统的1 024 点杂波数据提升到4 096 点可以增加IQ 信号的时长,进而提高杂波模拟仿真的精细程度。
Matlab 产生的杂波数据储存到RAM 时,数据读写的速度可能会有差异,因此使用乒乓RAM 的方式处理数据以克服数据输入输出速率不匹配的问题,实现连续读写[12],乒乓RAM 的结构图如图8所示。

图8 乒乓RAM 结构图Fig.8 Structure diagram of table tennis RAM
3.2 采样频率的提升
AD 采集到的输入信号经过数字下变频、FIR 滤波器和FIFO 延时后,会得到采样频率为1.5 GHz 的基带信号,但此时经过处理后的杂波数据采样频率为1.5 MHz。因此,需要对杂波数据进行内插处理,提高采样频率,以实现信号处理时的速率匹配[13]。
通过多个级联积分梳状滤波器(CIC 滤波器)进行内插以提升采样频率,内插前后数据对比如图9所示。
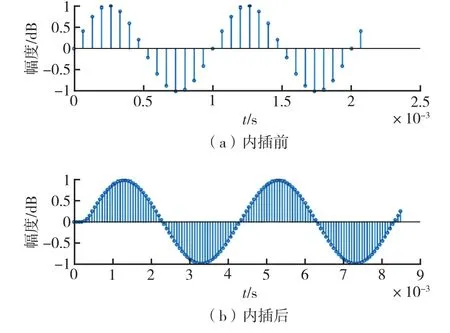
图9 CIC 滤波器内插对比图Fig.9 Comparison chart of CIC filter interpolation
多个CIC 滤波器级联结构主要由CIC 滤波器、插值单元和积分器组成。该结构成功实现了将杂波数据从1.5 MHz 采样频率提高到375 MHz 采样频率,其整体结构如图10所示。
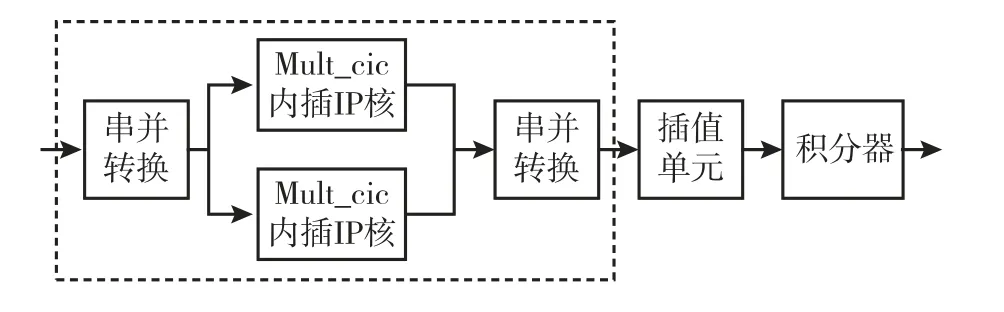
图10 CIC 滤波器结构图Fig.10 Structure block diagram of integral comb filter
对杂波的后续处理以及对回波信号的数字下变频、滤波、调制和数字上变频部分的实验均在System Generator 平台完成。
上位机产生频率控制字,通过DDS IP 核产生回波信号。将杂波信号与回波信号输入二选一多路选择器,通过flag 使能信号,选择输出回波还是杂波。IQ 两路杂波信号分别通过增幅模块,以提高杂波数据的功率。最终信号通过FIR 滤波器模块处理,将375 MHz 的杂波信号分为四相375 MHz 杂波信号,将总采样频率与基带信号的1.5 GHz 采样频率一致,四相IQ 数据被暂存,用于后续的数字正交调制,整体结构如图11所示。

图11 杂波IQ 信号产生原理图Fig.11 Schematic diagram of spurious IQ signal generation
3.3 数字射频存储
中频信号经过数字射频存储(DRFM)进行复杂波形调制处理,通过ADC 转化为数字信号,再将中频信号首先通过数字下变频得到零中频信号,转换后的数字信号经控制器采集后,存入高速实时存储器中,FPGA 作为控制器和数据处理器,对信号和杂波信号进行数字正交调制,数字上变频转换成模拟中频信号,最终将调制好的信号通过DAC 转化为模拟信号,完成输出,整体流程如图12所示。
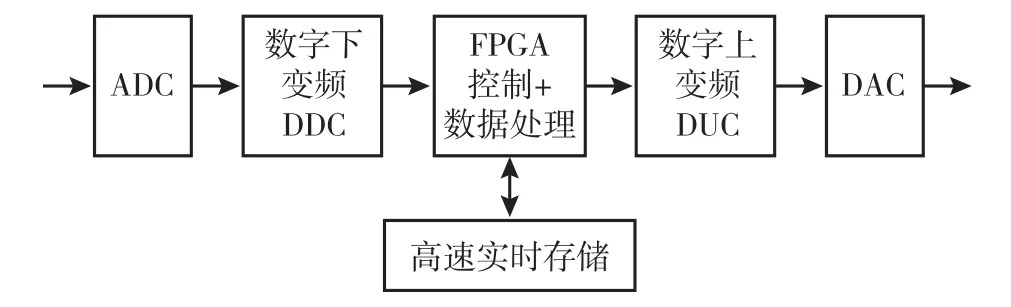
图12 数字射频存储流程图Fig.12 Flow chart of digital radio frequency memory
3.3.1 数字下变频
数字下变频模块使用Sysgen 搭建,主要由分相器、零中频模块和FIR 滤波器3 部分组成,整体架构如图13所示。
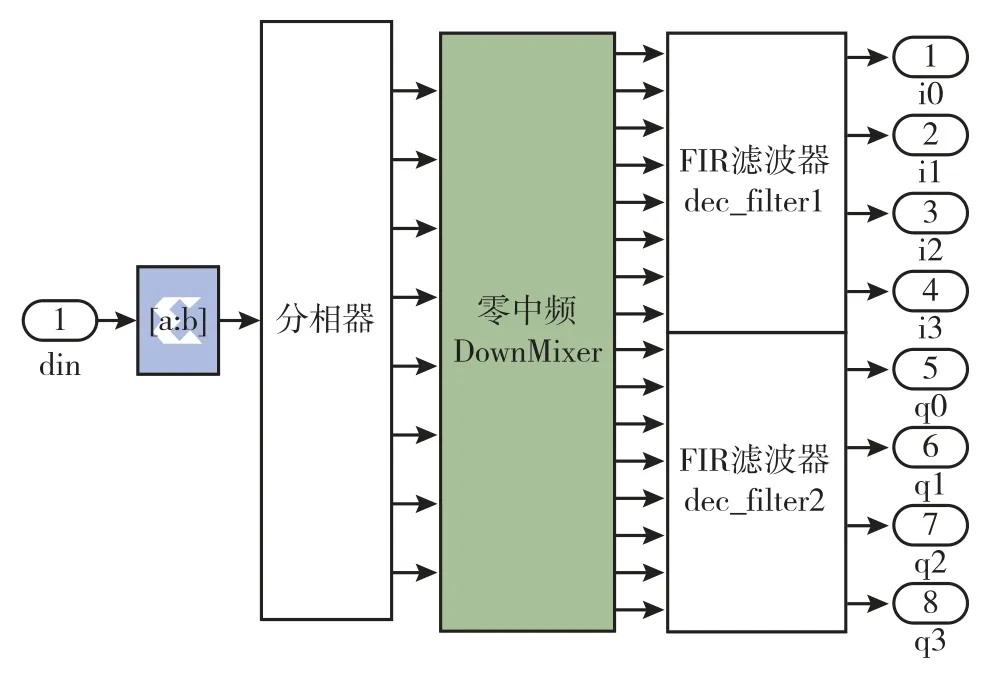
图13 数字下变频模块结构图Fig.13 Structure diagram of digital down conversion module
ADC 采集到的96bit 中频信号通过分相器分为8 路12bit 数据。目前基带信号为中频信号,与杂波信号相乘后,得到的信号频率会增加,提高了后续用于滤除冗余信号的FIR 滤波器的设计难度。因此将基带信号载频进行变频处理,变为零中频,便于后续乘法处理[14]。同时在零中频变频的过程中,可以将信号分为同相分量和正交分量,便于后续IQ调制。整体零中频结构如图14所示。
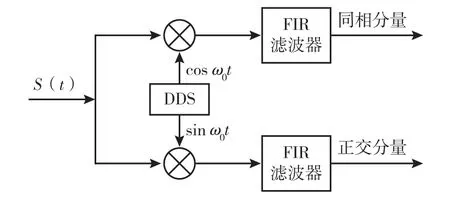
图14 零中频原理图Fig.14 Schematic diagram of zero intermediate frequency
假设中频信号s(t)满足:
零中频法产生同相分量与正交分量原理相同。以产生同相分量为例,基带信号与DDS 产生的中频余弦波相乘,并经过FIR 滤波器滤波。产生的同相分量表达式为:
FIR 滤波器设计采用多相结构,使用四个FIR滤波器并行多相处理,不同滤波器传输函数相同,通过改变不同滤波器输入信号的顺序,模拟数据的流水线传输,将信号处理速率提升到了原来的四倍。其原理如图15所示。
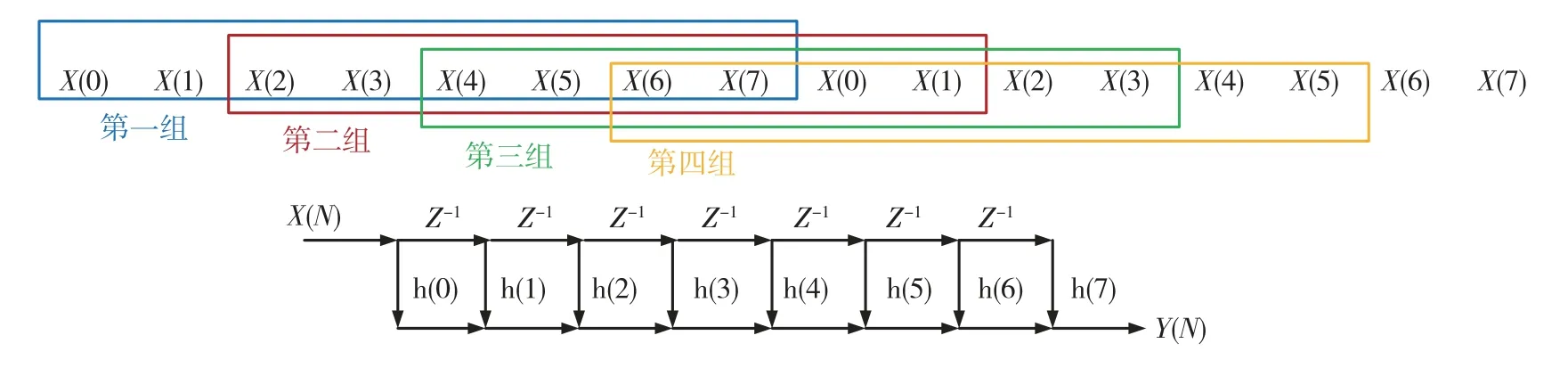
图15 FIR 滤波器的多相原理图Fig.15 Polyphase schematic diagram of FIR filter
3.3.2 多散射点的实现
在满足FPGA 数据处理硬件条件的情况下,通过精确刻画基带信号的不同延时量,可以提高散射点的数量。在此基础上,通过多个散射点并行实现基带信号与杂波的数字正交调制,可以实现雷达杂波的高精度模拟。
为实现多散射点延时,采用FIFO 作为数字抽头延时单元的基本模块。多散射点幅相信息调制是通过复域调制器实现的。复域调制器可以为多散射点目标提供不同的延时、幅度、相位和角度信息。整体结构如图16所示。
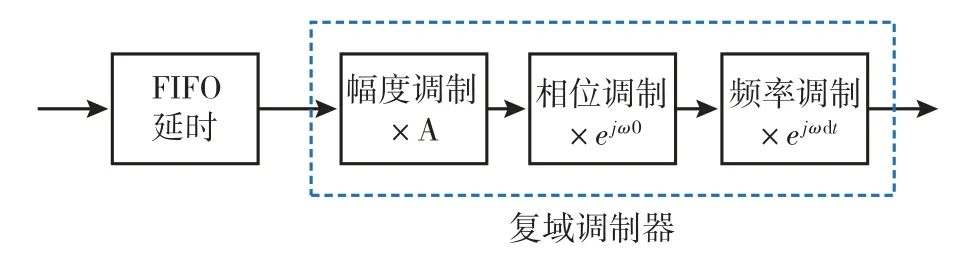
图16 多散射点的实现流程图Fig.16 Flow chart for the implementation of multiple scattering points
散射点数越多,模拟方法的精度越高。在时域中,高精度模拟主要体现为等距离环数量较多、划分较细,每个环之间的延时量不同;在频域中,则体现为谱线数量更多,间距更窄,能够更精细地刻画相同面积区域。
以回波信号调制后的频谱为例,通过频谱仪测量观察不同散射点信号的频谱图。可以看出相较于16 个散射点的信号,64 个散射点的回波信号频率分辨率数值更小,模拟精度更高,如图17所示。
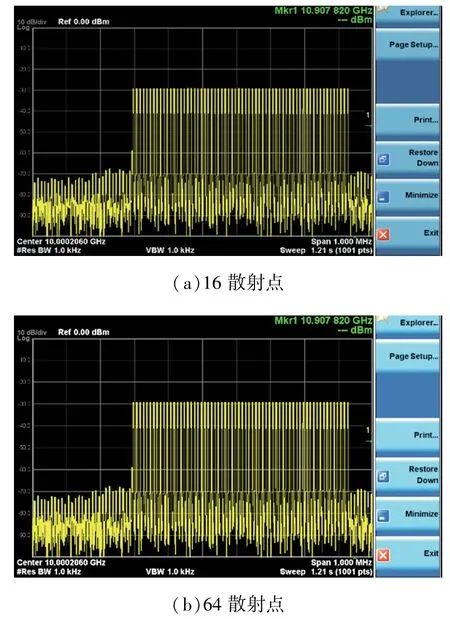
图17 16 和64 散射点回波信号的频谱图Fig.17 Spectrums of echo signals at 16 and 64 scattering points
3.3.3 数字正交调制
数字正交调制模块主要由5 部分组成,如图18所示。
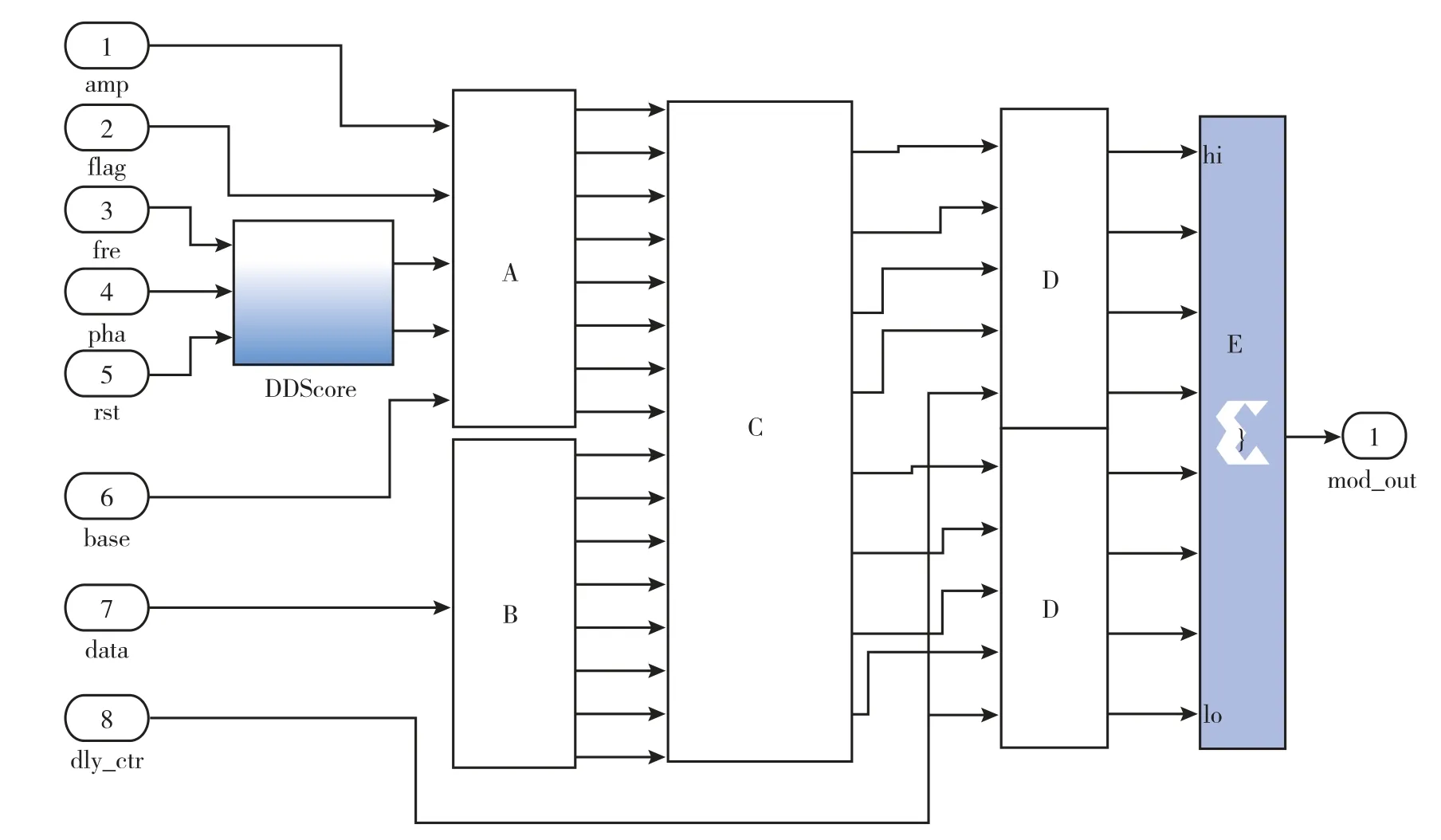
图18 数字正交调制结构图Fig.18 Structure diagram of digital quadrature modulation
模块A 是一个二选一多路选择器,可以选择输出杂波信号或回波信号,并对输出信号进行增幅调制。
模块B 是一个滤波器,将768 bit 的雷达基带信号分成了96 bit 的I、Q 信号,每路信号分成了4 路。
模块C 是数字正交调制的核心——乘法器模块,将8 路杂波信号I、Q 数据和8 路基带信号I、Q 数据通过4 组并行的乘法器模块做乘法运算,实现了单个散射点目标杂波信号与基带信号的调制。
模块D 是一组精延时模块。使用4 个并行的四选一多路选择器,当控制单元分别为00/01/10/11 时,四选一多路选择器选择不同的输出。循环调整控制单元的值,即可实现数据的流水线输出。通过四相结构,可以实现1/4 个时钟周期的精细化延时。同时通过控制单元的编码方式可以自由调整。
一组四选一多路选择器结构如图19所示。
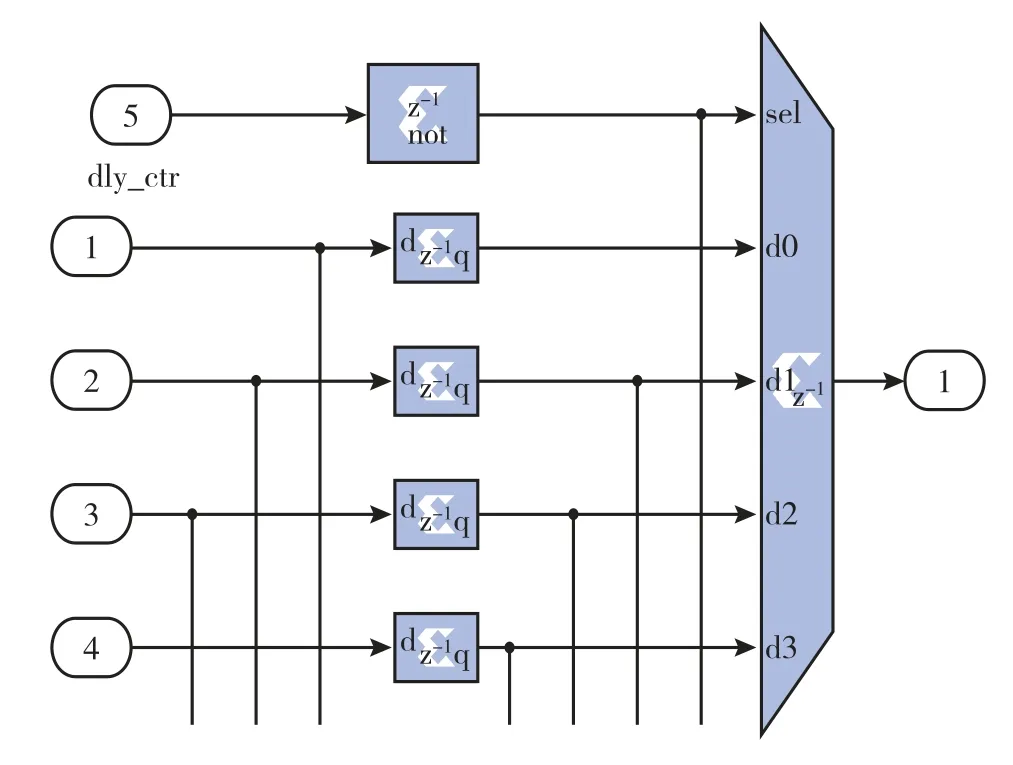
图19 四选一多路选择器结构图Fig.19 Structure diagram of four to one multiplexer
模块E 为位拼接模块,实现了将数字正交调制后的多路信号拼接成位数更高的单路信号。
在充分考虑计算FPGA 硬件计算能力的前提下,通过64 个数字正交调制模块并行结构,实现了杂波的高精度模拟。每个模块代表一个等距离环,其基带信号的延时不同。64 个散射点信号经过滤波、拼接后合并,再经由数字上变频模块重新转化为中频信号。最终经过DAC 完成输出。
4 结束语
介绍了等距离环的划分、雷达杂波建模与仿真的相关方法,以DRFM 为核心框架,设计了将Matlab 产生的杂波数据与基带雷达信号进行数字正交调制的雷达杂波模拟方案。该方案架构较为完善,有较高的实际工程应用价值。构建的高精度雷达杂波模拟方案可用于多种不同场景的雷达杂波仿真,系统信号带宽较高,实现瞬时模拟64 个散射点×4 096 个数据单元,提高了杂波模拟的精度。该理论对后续开展半实物仿真和模拟器硬件研制有着较高的参考价值。
