船载天线的故障诊断与动力学分析
2023-04-06郭刚涛张正谦马新生王淑萍
郭刚涛,张正谦,孔 萌,马新生,王淑萍
(西安航天天绘数据技术有限公司,陕西 西安 710100)
0 引言
随着我国北斗导航系统的成熟及移动通信的快速发展,船载天线用户激增。由于海上使用环境较为恶劣,长期的颠簸及盐雾环境对天线系统中的机械核心部件可靠性要求较高[1]。作为船载天线承力最大、受力情况最复杂、运动最频繁的方位轴承,也是天线最容易出现故障的部件,如能根据实时检测数据进行故障诊断将可实现天线故障预警,保障船体运行中通信正常,最大程度上防止因机械故障造成的船只失联。
目前,故障诊断在汽车、飞机发动机和精密机床等设备上有较广的应用[2-5],但在船载天线方面的研究较少。本文以混沌系统为理论基础,采用六自由度摇摆台来模拟环境条件,搭建数据采集平台对故障轴承数据进行采集,将故障信号加入变形Rossler 混沌系统来进行故障诊断并成功检测到故障信号频率,通过定量的计算来确定故障信号真实存在,为船载天线传动机构故障诊断与预警提供了一定的思路。
1 混沌振子系统模型建立
1.1 Rossler 系统
Rossler 系统[6]的灵感来源于经典的Lorenz 系统,所以两者在形式上十分相似,两者都是具有混沌行为的非线性方程组,但Rossler系统比Lorenz系统更加简单化,而且拓扑是不等价的,即不存在任何同等变换可以把一个系统变为另一个系统。Rossler 系统的具体形式如下所示:
式中:a,b,c为系统的控制参数;x,y,z则为系统的状态变量。当a,b取2,参数c取5.7 时,此时系统处于混沌状态。
1.2 变形Rossler 系统
通过对Holmes 型Duffing 方程的研究后发现,该非线性方程中含有周期策动力信号rcos(ϖt),在对微弱正弦信号的检测中,周期策动力信号对整个混沌系统的影响是非常大的,使得整个系统对噪声具有良好的免疫性。将周期策动力信号加入到原始Rossler 系统,使整个系统对于微弱信号更加敏感,整个系统对噪声具有更好的免疫性。其中,变形Rossler 系统[7-9]的具体模型如下所示:
式中:a,b,c为系统的控制参数;x,y,z为系统的状态变量;rcos(ϖt)为周期策动力信号。
2 环境模拟及数据采集
船载天线选用0.8 m 口径两轴稳定转台天线,天线整机由天馈组件、俯仰机构、方位机构和方位底盘等组成,如图1 所示,其方位轴承为内圈点蚀故障轴承。

图1 船载天线结构图
选用MOTUS 公司MTC-6DOF 型号六自由度摇摆台,最大可承载1 000 kg 的重量,可完全满足0.8 m 船载天线的使用。该平台精度高、响应快,最大摇摆幅度可达15°,最大运行速度为30(°)/s,最大加速度为50(°)/s2,可根据船载天线使用工况,最大程度上模拟海上实际运动环境。摇摆台实物图如图2 所示。

图2 摇摆台实物图
根据海测数据对摇摆台参数进行设置以模拟海上环境,摇摆台参数设置如表1 所示。
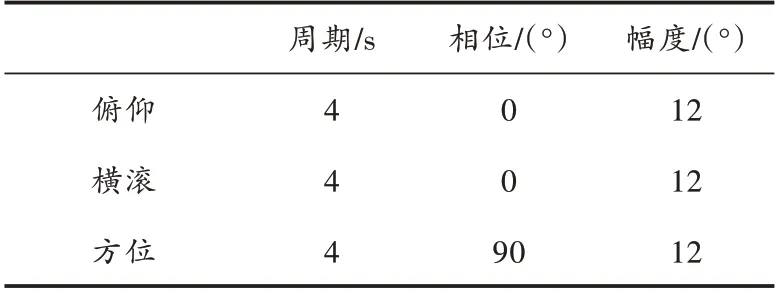
表1 摇摆台参数
模拟船载天线圆锥扫描过程中运动轨迹,考虑到天线响应需满足动中通特性,方位机构在运动过程中最大转动速度为200(°)/s,故在试验过程中,用上位机设定天线方位转动速度为200(°)/s,俯仰保持在45°位置以模拟对星位置,天线测试系统实物图如图3 所示。

图3 天线测试系统实物图
由于天线故障信号较微弱,为提高信号采样率,本系统在方位轴承内圈附近等间距布置4 个高精度三向加速度传感器,可同时兼顾三个方向加速度数据,采用DEWTRON 公司动态信号采集仪进行采样,采样频率为1 kHz,图4 为信号处理软件数据处理界面。
图4 数据采集软件界面
3 方位轴承故障分析
3.1 方位轴承常见故障
方位轴承常见的故障有:疲劳剥落损伤故障、磨损类故障、结构变形故障和螺栓松动故障[10]。由于船载天线连续工作时间长、环境恶劣,还要承受海水盐雾腐蚀,所以疲劳剥落损伤最易发生。
点蚀属于疲劳剥落损伤故障,在船载天线运行过程中,由于海浪的颠簸会使方位轴承受力不均匀,加上盐雾环境会加剧点蚀故障的发生概率。点蚀可发生在轴承外圈、内圈或滚动体上,此次测试系统中方位轴承故障为内圈点蚀故障,其型号为无齿型010.10.100 回转轴承,内圈直径为90 mm,外圈直径为110 mm,滚珠直径为10 mm,滚珠数量为25 个,轴承实物图如图5 所示。

图5 故障方位轴承
3.2 故障特征频率计算
当船载天线方位转动时,方位轴承每次通过局部损伤点(内圈点蚀故障)都会发生碰撞,每当发生碰撞的时候,信号的能量和幅值就会发生突变而出现尖峰,这种能量波动也会引起回转支承,回转支承产生衰减性振荡,人们把这种出现能量突变时的频率叫作故障特征频率。
影响故障特征频率的主要因素有转动速度、回转直径和点蚀位置等,轴承内圈、外圈、滚动体故障特征频率计算[11]分别如下所示:
式中:α为轴承的接触角;fir为内圈旋转频率;Z为滚珠数目;D为轴承滚道直径;dw为滚珠直径。
由此可得方位轴承内圈故障特征频率为7.63 Hz,外圈故障特征频率为6.25 Hz,滚动体故障特征频率为5.49 Hz。
4 故障诊断及仿真分析
4.1 故障诊断
Lyapunov 指数[4,12]和Lyapunov 维数可以定量地描述一个系统的混沌特性,本文采用Wolf 方法计算Lyapunov 指数。Wolf 法特点是时间序列无噪声,空间中小向量的演变高度非线性,对混沌时间序列采用C-C 方法求取计算嵌入维和延迟时间,然后重构相空间,最后用最小二乘法进行直线拟合求最大Lyapunov 指数。
当系统处于混沌运动状态时,求解器最大Lyapunov指数总是大于0;当系统处于周期运动状态时,求解器最大Lyapunov 指数总是小于0;当求解器最大Lyapunov指数等于0 时,各点对应分叉点。
加入故障信号之前:计算Lyapunov 指数为:λ1=0.003 22,λ2=-0.013 78,λ3=-2.687 9。由计算结果可知,最大Lyapunov 特性指数大于0,说明系统处于混沌状态。
下面计算系统的Lyapunov 维数[13]:
由此可见,这个变形的Rossler 系统的Lyapunov 维数是分数维数,从而验证了该系统是混沌运动状态。
加入故障信号之后,计算Lyapunov 指数为:λ1=-0.027 37,λ2=-0.112 68,λ3=-6.323 3。由计算结果可知,最大Lyapunov 特性指数小于0,说明系统处于周期运动状态,通过定量计算可得出轴承内圈故障特征频率存在。
4.2 仿真分析
为了模拟轴承故障对天线整机的影响,采用UG 动力学模块对天线整机进行振动分析。首先对天线整机进行有限元处理,利用有限元前处理软件的模型检验功能进行了自由边检查、单元重叠性检查和Jacobi 行列式检查等,保证有限元模型的正确性。整机有限元模型如图6 所示。
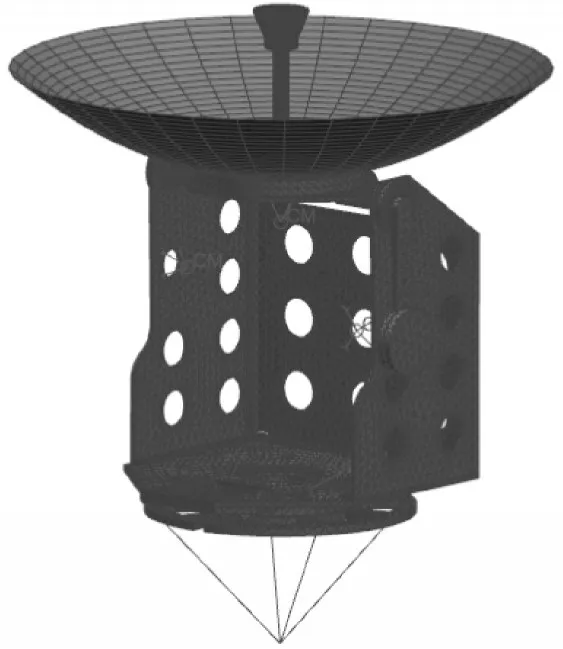
图6 整机有限元模型
振动参数在摇摆台参数外还额外增加方位轴承内圈故障特征频率7.63 Hz,通过动力学分析估算求解控制参数,结构的振动特性决定了结构对各种动力载荷的响应情况,天线整机采用铝2A12 材料,屈服强度为255 MPa。通过仿真可以看出:在摇摆参数影响下,天线最大应力为137.64 MPa,整机受力云图如图7 所示。在摇摆参数和故障频率影响下,天线最大应力为150.58 MPa,增加了12.94 MPa,如图8 所示。由此可见故障频率的存在会造成天线自身应力的增加,影响天线的性能,缩短天线的使用寿命。

图7 加入故障频率前应力云图

图8 加入故障频率后应力云图
5 结论
随着我国卫通事业的快速发展,船载天线的数量日愈增加,在线监测及故障诊断的需求也愈加强烈;混沌系统作为故障诊断中的新兴理论,工程应用越来越多,但在船载天线领域应用较少。本文将混沌系统应用于船载天线故障轴承之中,结论如下:
1)以船载天线为研究对象,搭建了六自由度试验平台模拟船载天线运动环境,为船载天线乃至卫通天线传动故障方面的研究提供了一些参考。
2)将变形Rossler 混沌系统应用于船载方位轴承故障诊断,为混沌系统的工程应用及推广提供了一些参考,也为轴承的故障诊断提供了一些新方法。
3)使用动力学仿真对故障频率进行仿真,对天线故障频率的影响进行了量化,为船载天线的故障诊断提供了支撑。
