海底膨胀弯法兰姿态测量方法
2023-04-06屈庆轩朱绍华隋海琛阳凡林
屈庆轩 朱绍华 秦 建 杨 鲲 隋海琛 阳凡林
(1. 山东科技大学 测绘与空间信息学院, 山东 青岛 266590;2. 海洋石油工程股份有限公司, 天津 300461;3. 天津水运工程勘察设计院有限公司, 天津 300456)
0 引言
随着海洋开发事业的蓬勃发展,将来会有越来越多的海底管线铺设到海底[1-2],海底管道是通过密闭的管道在海底连续地输送大量油(气)的管道,这就必然伴生出法兰膨胀弯的连接工程[3-4]。而所谓海管膨胀弯的连接,是指在导管架立管底部和海底管线平管之间用法兰和膨胀弯进行连接。如图 1所示,膨胀弯由法兰、直管段、弯头、锚固件(混输管线)等附件组成,是为了补偿因温度差与机械振动引起的附加应力,而设置管道上的一种挠性结构[5-7]。利用其工作主体管的有效伸缩变形,可以吸收管线由热胀冷缩等原因而产生的尺寸变化,或者补偿管线的轴向、横向和角向位移。而膨胀弯的连接最关键的工序就是待连接两法兰的姿态和距离的测量[8-9],能否准确测得水下膨胀弯连接处法兰的姿态关系着膨胀弯是否能顺利地预制安装。
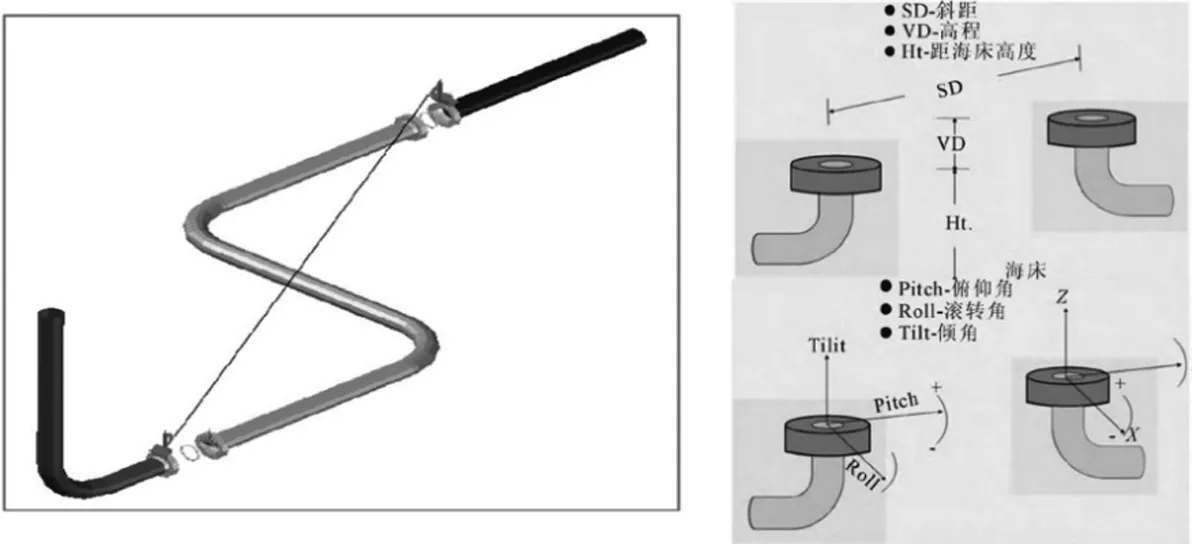
(a)膨胀弯整体示意图 (b)膨胀弯测量要素
国内对于膨胀弯水下测量方法的研究起步较晚,在实际的水下膨胀弯测量安装项目上,主要使用依靠潜水员为主的水下法兰测量仪直读式测量方法,该方法易受法兰测量仪测距钢丝自重、海流及潜水员读数影响,导致测量结果与真实数据之间存在一定误差,而且受两法兰间距离影响较大,距离越长,法兰测量仪所引入误差越大。陶杰等为了提高法兰测量仪的精度,对其进行数学建模(异面直线的位置关系),从理论上分析其数学模型的误差,对于法兰测量仪所测数据进行误差补偿[10],姜学录等利用法兰测量仪对水下法兰姿态进行精确测量,并按照测量数据在岸上指导膨胀弯的制造,顺利完成了渤海湾某油田工程的膨胀弯安装工作[11],本文提出了一种姿态测量误差修正方法,想较于传统的法兰测量仪,可以精确、快速地测量法兰姿态,且不受水深和法兰间距影响。
全站仪作为一种高精度的测量设备,广泛应用在对陆地上的物体进行三维坐标测量[12-13],对坐标数据进行提取和处理后经过三角函数计算可以获得待测目标的姿态信息。这种方法的计算过程并不复杂,但是存在以下缺点:一是受到系统误差、偶然误差及粗差的影响,测量精度会降低;二是受待测物体表面的不平整度影响较大,受到加工精度的影响,待测平面不一定为绝对水平面,但是全站仪获得的是单个点坐标,并不能代表整个平面;三是受待测物体大小影响,如果待测平面为大型平面,其平面上各个特征点基线距离较长,测量精度较高,相反如果待测面为小型平面,特征点较为密集,精度就会降低。
由于水下环境的局限性,全站仪不能用于水下海底管道法兰的姿态测量。通常使用惯导(inertial navigation system,INS)等水下姿态测量仪器来替代全站仪进行姿态测量,使用较为方便。惯导等设备在测量安装时,会引入仪器轴线与待测平面不平行的安装误差。本文提出了一种姿态测量方法,在用惯导等姿态测量仪器测量目标姿态时,可以有效解决安装误差对测量精度的影响,提高膨胀弯法兰姿态测量精度。
1 姿态定义及误差来源
1.1 姿态角定义
以法兰端面圆心点O为坐标原点,Y轴垂直于法兰端面并指向法兰朝向,X轴平行于法兰端面,Z轴沿法兰端面向上并与X-O-Y平面垂直,建立如图2所示的法兰端面右手坐标系,X轴、Y轴、Z轴分别为该法兰坐标系的三个坐标轴。
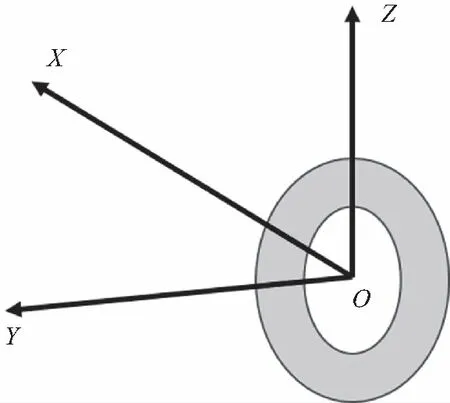
图2 法兰坐标系
以当地水平面为基准面,定义法兰坐标系在Y轴方向上围绕X轴旋转产生的角度为俯仰角Pitch,当法兰后倾时Pitch为正,前倾时为负;定义法兰坐标系在X轴方向上围绕Y轴旋转产生的角度为横滚角Roll,以法兰艏向起始,左高为正,右高为负[14-16]。
1.2 安装误差来源
在使用惯导测量平面姿态时,通常将惯导放置在待测平面上进行数据采集。图3为常规姿态测量时的仪器安装图示,对测得艏向俯仰角Pitch进行分析,以点O为坐标原点,分别建立X轴平行于水平面,Y轴垂直于水平面向上的X-O-Y坐标系;建立X′轴平行于待测平面指向平面艏向,Y′轴垂直于待测平面向上的X′-O-Y′坐标系;建立X″轴平行于仪器水平轴线指向平面艏向,Y″轴垂直于艏向轴线向上的X″-O-Y″坐标系。对于横滚角Roll来说,该系列坐标系应往艏向右方向旋转90°。
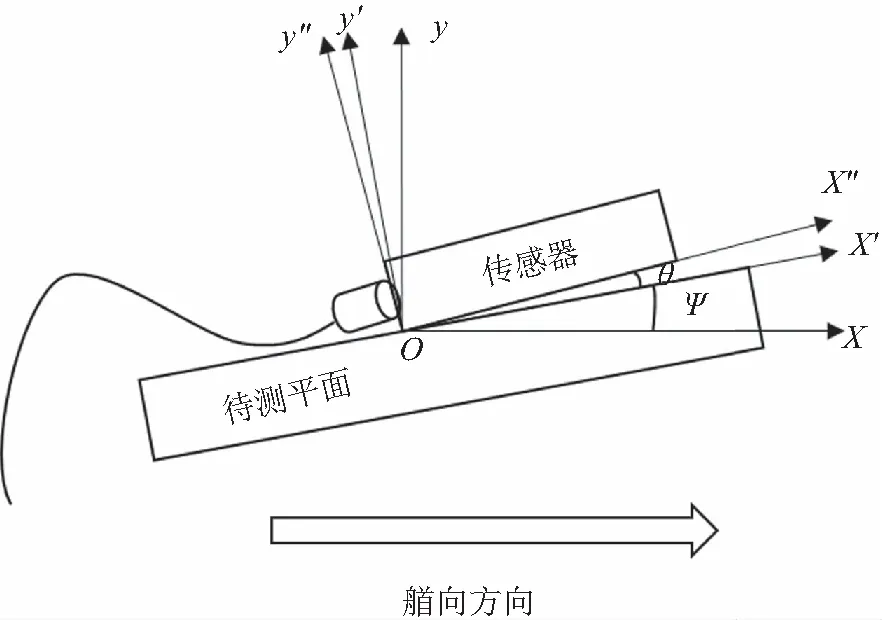
图3 按艏向安装
其中X’轴和X轴的夹角ψ即为待测平面的实际俯仰角,X″轴和X′轴的夹角θ为仪器与待测平面之间的安装误差角,而仪器测得的显示角度为实际待测平面角ψ和误差角θ之和,俯仰角和横滚角相同。如果待测平面和传感器底面非常标准且平整度较好,此安装误差应该较小,但是随着设备寿命的增加和仪器运输过程中的磕碰影响,以及安装时两接触面不完全贴合,造成传感器轴线与待测平面轴线不平行而引起安装误差。如果能在测量工作中测得仪器的俯仰角和横滚角的安装误差并在数据计算中加以改正,姿态测量精度会大大提高。
2 误差测量方法
针对于水下膨胀弯姿态测量安装误差的影响,本文提出了一种测量方法,该方法的测量原理如下:对待测平面进行姿态测量时,因为安装误差始终贯穿整个测量过程,理论上属于系统误差的一种,而且其误差值在每次测量中具有一致性,所以可以通过调整姿态测量仪器的方向并配合合理的数据处理方式进行消除。
对于俯仰角来说,如图3、图4所示,首先以待测平面艏向安装仪器,连续测量后可得该方向的俯仰角Pitch1,然后将该仪器旋转180°,测得与艏向相反方向的俯仰角Pitch3。由上面分析得到的误差关系可知测得角度受到安装误差角θ和待测平面角ψ的影响实际为
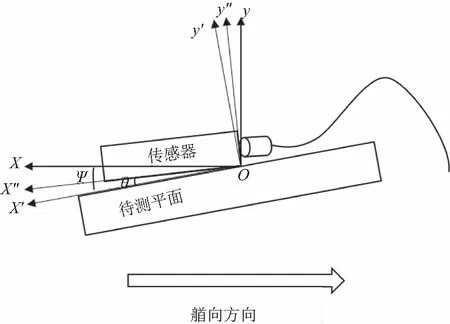
图4 反艏向安装
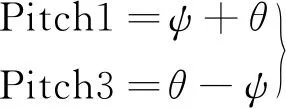
(1)
由上式可得
(2)
角θ即为艏向方向上仪器的安装误差ΔPitch1-3。
同理将仪器按照待测平面艏向方向向右顺时针旋转90°测得该方向俯仰角Pitch2,然后将该仪器旋转180°,测得与该方向相反方向的俯仰角Pitch4。由误差关系可得
(3)
角θ′即为艏向方向上仪器的安装误差ΔPitch2-4。
对于横滚角同理,将仪器安装在待测平面上,旋转四个方向后可得四个方向横滚角观测值Roll1、Roll2、Roll3、Roll4以及安装误差角ΔRoll1-3、ΔRoll2-4。
根据观测值与安装误差角度的关系,由公式(2)、(3)可以分别计算出该待测平面的四个俯仰角实际值Ptich1′、Ptich2′、Ptich3′、Ptich4′和四个横滚角实际值Roll1′、Roll2′、Roll3′、Roll4′。
(4)
(5)
3 实验数据采集及分析
在水下测量海底管道间的空间关系时,需要将设备安装基座固定在海底管道法兰上,基座上安装设备来测量法兰姿态。本次实验在陆地上模拟海底情况,首先将设备基座固定在一平面上,使用全站仪多次测得基座各特征点坐标,经数据处理后得到基座结构的姿态角初始值;而后在基座结构上安装惯导来测量基座的姿态,通过文中所述方法对惯导数据进行处理后与全站仪所测基座真实姿态作对比。如图5所示为设备安装基座结构。
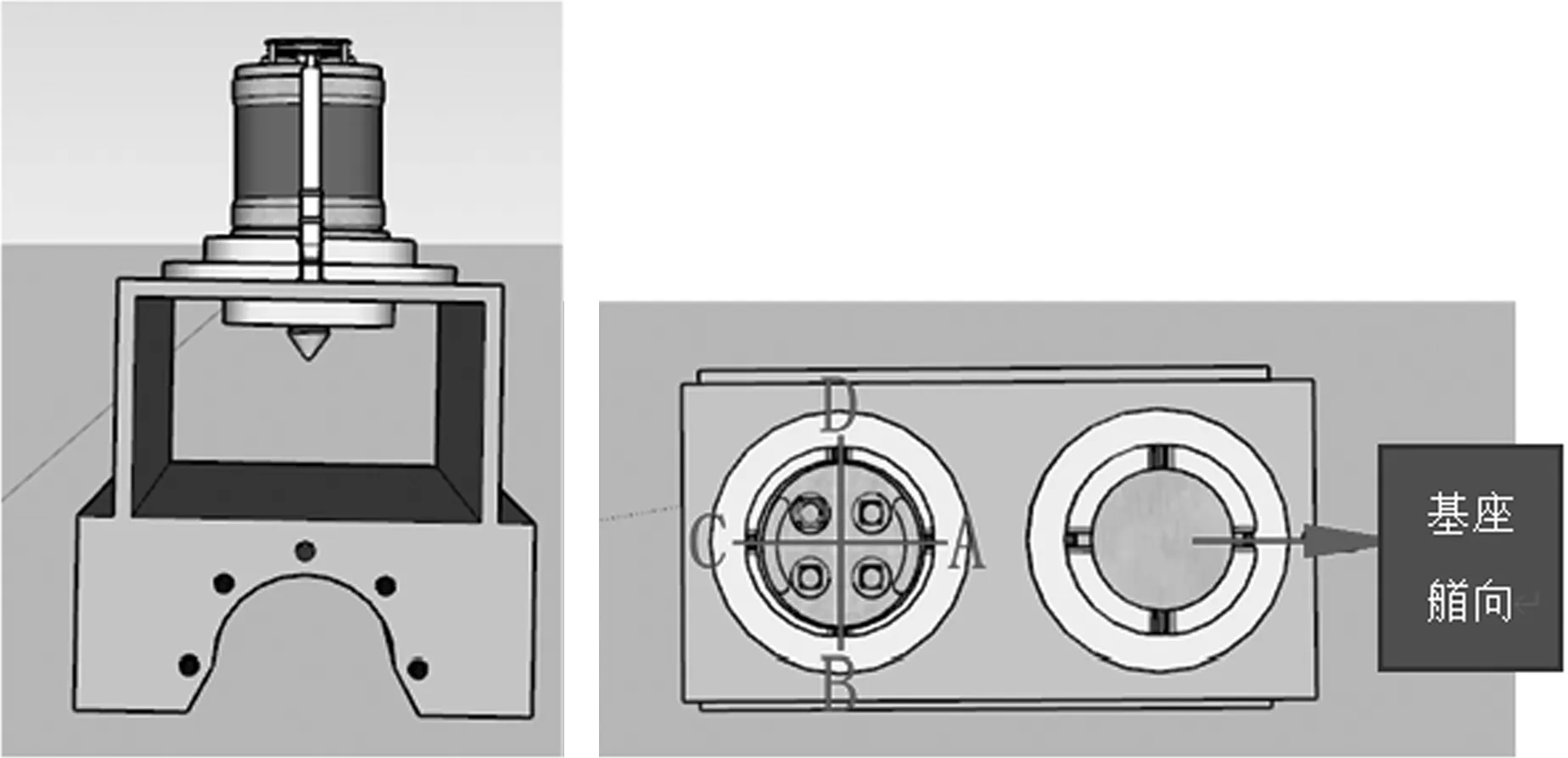
(a)主视图 (b)俯视图
如图5所示在安装基座上定义与基座艏向平行的安装方向为A方向,然后以艏向为基准顺时针旋转90°为B方向,由B方向继续顺时针旋转90°为C方向,右C方向继续顺时针旋转90°为D方向。
3.1 全站仪数据采集与处理
本次实验采用徕卡TM50高精度全站仪采集基座特征点坐标来计算基座初始姿态,具体流程如下所示:
(1)在设备安装基座上不同方向设置若干测量特征点。
(2)已知控制点上架设全站仪,多次采集特征点三维坐标。
(3)数据处理,计算基座初始姿态。
已知各特征点坐标后,根据距离和角度的三角函数关系可得对应角度σ公式为
(6)
其中,σ为待计算姿态角;ΔX、ΔY、ΔZ分别为对应特征点的坐标差值。最后测得基座初始状态如表1所示。
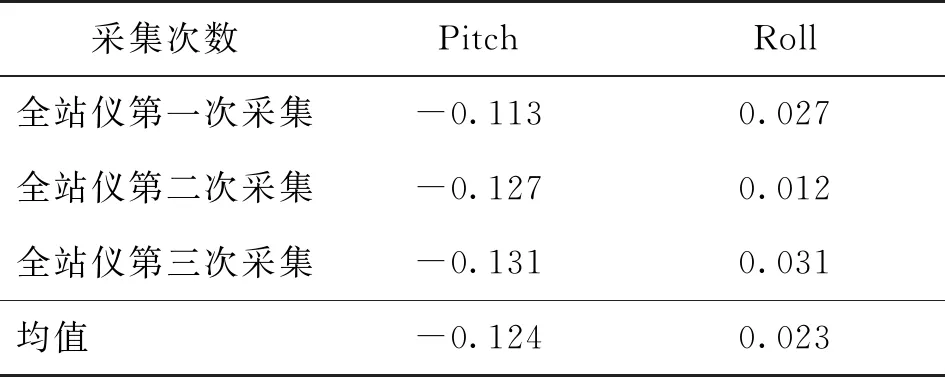
表1 基座初始姿态 单位:(°)
实验中使用全站仪测得三组同一基座初始姿态值,可以得出其Pitch均值为-0.124°,Roll均值为0.023°。
3.2 惯导数据采集
将惯导安装在法兰基座上,通电后进行连接设置,因为其纬度对测量精度有影响。所以需要通过loadstar软件对惯导纬度进行设置,稳定2 h以后,从定义的A方向开始,采集10 min姿态数据,然后依次旋转90°在B、C、D方向上进行惯导姿态数据采集。
在用惯导采集基座结构的姿态信息时,由于惯导采集的姿态数据随着采集时间的增长越发稳定,所以每个方向上选取最后时间采集的50组数据参与计算。
3.3 惯导数据分析
(7)
(8)
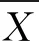
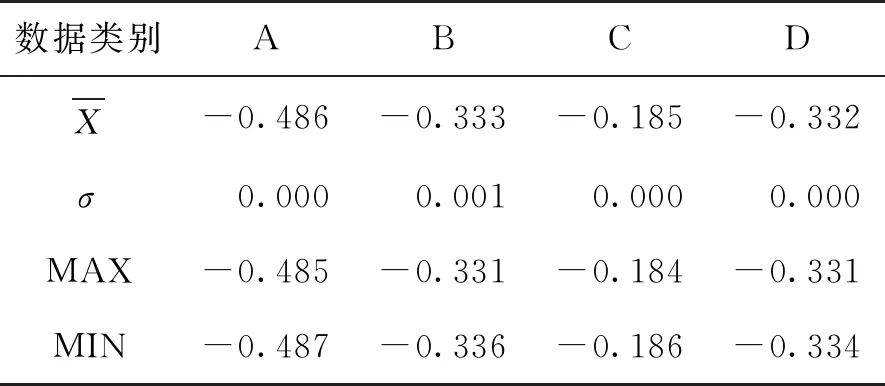
表2 俯仰角(Pitch)数据精度 单位:(°)
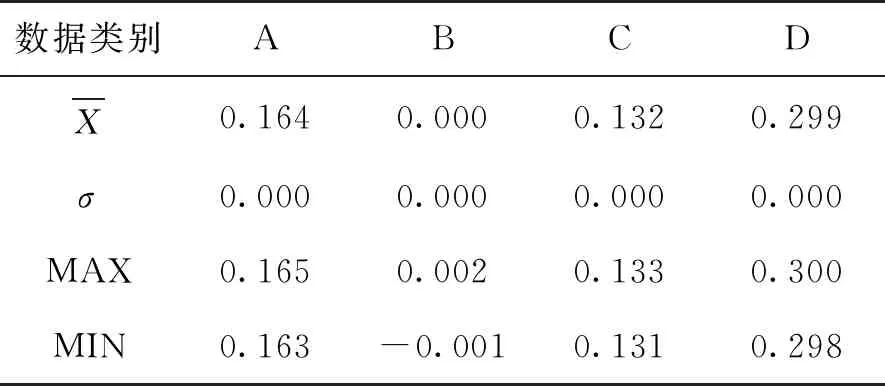
表3 横滚角(Roll)数据精度 单位:(°)
从表2、表3可以看出俯仰角四个方向最大值和最小值之差最大为0.005°,横滚角四个方向最大值和最小值之差最大为0.002°。俯仰角和横滚角四个方向数据标准差最大为0.001°,说明数据比较稳定,所以分别取每个方向上的俯仰角和横滚角平均值进行安装误差角的计算。
表4为左侧为处理后的每个方向的Pitch和Roll观测值,通过使用文中方法计算后得到两组安装误差角。由A、C两方向观测值所计算的误差角度Pitch为-0.335°,Roll为0.148°;由B、D两方向观测值所计算的误差角度Pitch为-0.333°,Roll为0.150°。两组误差角度Pitch和Roll的分别差值都为0.002°,差值很小,可以用来对观测值进行改正,改正后每个方向的实际值如表5所示。
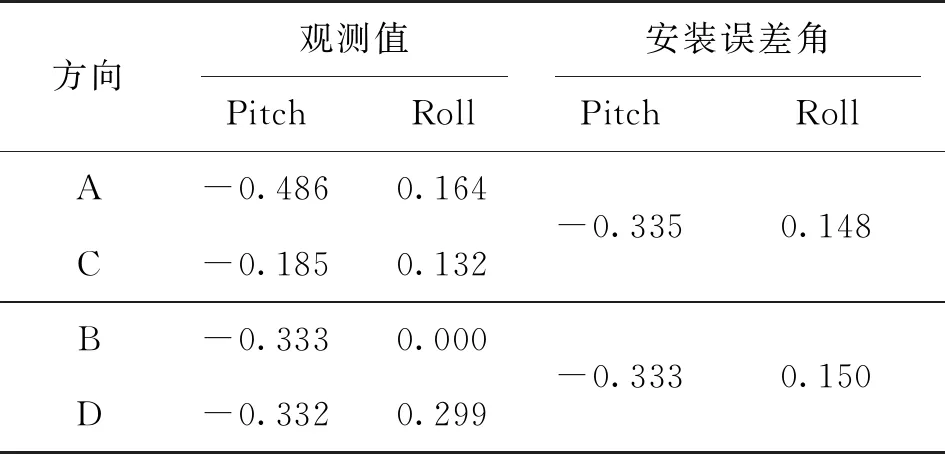
表4 安装误差角计算 单位:(°)

表5 姿态结果计算 单位:(°)
将改正后的每个方向上的Pitch和Roll值统一归化到A方向,即与全站仪数据结果的方向统一后,得到四组实际值如表5左侧所示。分别对四组实际值计算器Pitch和Roll值标准差,Pitch标准差为0.001°,Roll标准差为0.008°,数据较稳定,最后得到利用惯导采集的基座姿态均值,Pitch为-0.150°,Roll为0.008°。
表6为全站仪所测基座姿态和惯导观测值以及改正后惯导实际值之间的比对,可看出由于安装误差角的存在,使得惯导观测值与全站仪观测值Pitch存在0.362°的误差,Roll存在0.141°的误差;经过文中方法改正后的惯导测量实际值与全站仪观测值之间的误差明显减小,Pitch误差为0.026°,Roll误差为0.015°,均在0.05°的要求精度内。

表6 数据比对 单位:(°)
4 结束语
本文针对水下结构物姿态测量时由于仪器安装误差的存在使得测量精度降低的问题,提出了一种姿态测量方法,通过全站仪测量数据与惯导处理数据进行对比,证明该测量方法可以在一定程度上削弱仪器安装误差对测量精度的影响,提高姿态测量精度。在实际应用中,需要考虑到所选测量仪器本身量程是否满足项目工程的需要,以及在深水条件下测量操作的准确性。本文不足之处是没有设计水下实验进行姿态测量,后续还需要设计更完善的实验进行验证,文中所提及的姿态测量方法也可对陆地上同类型问题的解决提供思路。
