基于数据稀疏特征的架空电力线路故障可视化运检技术
2023-04-06刘晓晶陈显达王婷婷
刘晓晶,陈显达,曹 帅,陈 楠,王婷婷
(1.国网济南供电公司,山东 济南 250000;2.山东送变电工程有限公司,山东 济南 250000)
由于架空高压电线电缆长期在外界环境中,经历风雨雷电等不同天气,相较于其他电力设备而言发生故障的概率较高,一旦电线电缆发生故障,极有可能影响人们的生产生活,若出现架空电线接地故障的情况,亦会造成安全隐患,因此,对架空电力线路进行精确的运维检测是十分必要的,准确定位的同时,可以快速完成电路检修,减少故障带来的生产生活影响,保证供电可靠性。
对此,董新洲等[1]研究了一种弧光高阻检测法,建立弧光高阻线路接地故障检测模型,通过测量线路的实际电源微弱程度,解析线路故障点附近的等效虚拟电源,以及在电源影响下出现的零状态响应电流密度特性,通过解析线路中电流密度变化的稳态频域和时域,完成对电力线路的故障检测;丁佳立等[2]研究出一种行波故障检测法,测量线路两端及中点区域的输出电流和行波,通过皮尔逊相关系数分别比较线路电流信息,从而锁定故障点所在的线路范围,凭借测算故障额定电流的传输时间误差及行波速率,确定线路故障具体情况及位置。但以上两种方法都需要大量完整的数据,才能够实现线路故障的有效运检,对数据质量要求较高。
为此,本文基于数据稀疏特征,挖掘和分析电力系统稀疏数据中隐藏的有用信息,分析线路中行波特点,确定故障位置点以及具体的故障情况,有效检测电力架空线路发生的接地故障,通过改变检测数据的聚集和离散程度,将数据汇聚成散点结构适当的散点图,完成电力线路信息可视化处理,没有过高的数据要求,且检测结果准确度高,可视化效果好。
1 架空电力线路的稀疏数据特征提取
电力架空式线路运维检测的过程中,因为受到外界诸多不确定因素的影响,所采集到的数据中可能会存在大量空值的稀疏数据,信息显示不完整,但并不代表所采集到的数据是完全失效甚至无用的,本文通过对稀疏数据进行相应的特征提取,可以从中分析出大量的隐藏数据和数值信息,以便于对电力架空线路实行更加精细化和细致化的故障运维检测。

X=[x1,x2,…,xn]∈Rd×n.
(1)
此时,可以求解数据的稀疏系数si[3]

(2)
式中:X′是不包括第i列中数据xi的稀疏数据矩阵,稀疏系数的n维向量表示为
si=[si1,…,sii-1,0,sii+1,…,sin]T.
(3)
将si中的第i个稀疏元素值设置为0,这时稀疏数据集合经过系数重构后,矩阵为

(4)
式中:S可拆解表示成

(5)
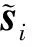

(6)
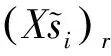
计算稀疏数据的中心距离特征
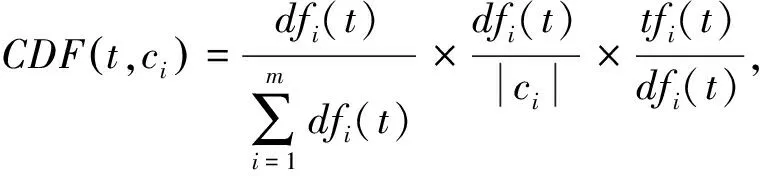
(7)

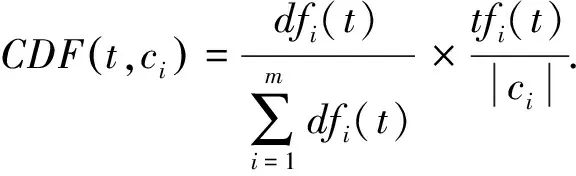
(8)
通过最大值算法计算式(8),求得稀疏数据中特征对数据分类的贡献程度

(9)
设定数据特征选择阈值,通过判断CDF值是否大于阈值,决定是否提取该特征,只有当CDF值大于设定阈值时,提取该特征才有数据分析意义。
2 电力架空线路故障检测
在已知故障行波速度的情况下,假设检测出的电力架空线路故障处的行波速度v,通过分析发生故障处的行波距离电力线路起终点间的运行时间,即可判断故障具体发生位置。
设电力架空线路的总长度为L(km),线路的起始点分别为P,Q,故障距离起终点的距离分别用p和L-p表示,故障行波沿着架空线路传送到起始点的时间分别为a,a′,电力架空线路的故障如图1 所示,此时各条件间的关系可表示为

图1 电力架空线路故障示意图
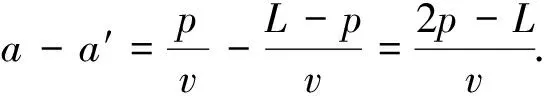
(10)
将式(10)简化运算可得

(11)
对于架空线路发生的接地和非接地类型故障,该算法均适用,但在实际的运维检测过程中,架空线路行波可能会受到各种不同因素的影响,例如配电线路的分布电容不均、土地电阻率发生变化或分布电感误差等影响因素,在不同影响因素下,都会导致架空线路故障检测发生一定的误差,这些情况按照行波速度未知来进行额外的具体判断。
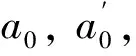
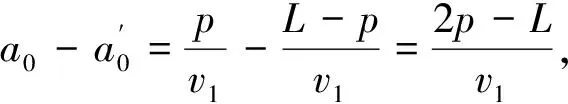
(12)
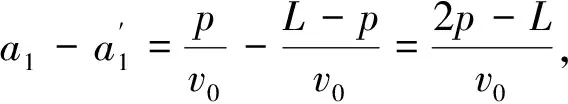
(13)
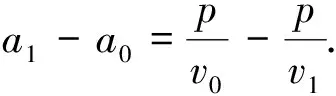
(14)
将式(12)~式(14)联立并简化运算可得

(15)
式(15)可用来有效检测电力架空线路发生的接地故障,由于架空线路之间存在着一定程度的间距,因此对于线路中存在的单相接地和线路故障的测距也同样有效。
在电力架空线路的起始点P处投放适量电容[7],这时,线路受到影响所产生的放电回路如图2 所示。

图2 故障回路示意图
图2 中,Z1表示线路中的等效电阻,G1表示分布电感,G0,R0是分别用于检测故障定位分布的电感和电容,线路故障点处提供过度行波的电阻用Zf表示。
改变电感G0和电容R0值的大小,以保证线路中电容放电的电流维持衰减震荡状态,使电路满足以下条件
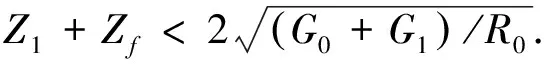
(16)
在此基础上,需要利用微分求解线路中的二阶电路,得出故障所在线路的起始点P处的放电电流I1
(17)
式中:λ1表示电路信号的振荡频率;β1表示信号传递的衰减系数[8];U0表示故障发生位置的架空高压线路两端电压;λ1,β1的具体表达式分别为

(18)
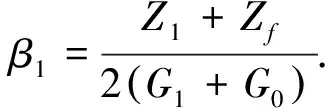
(19)
利用一阶分解法分解式(17)中的二阶电路,可以得到放电电流的振荡频率和具体的衰减系数,将式(18)和式(19)联立简化可得
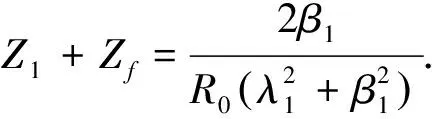
(20)
与上述原理相同,在故障所在线路的终点Q处投放电容可得
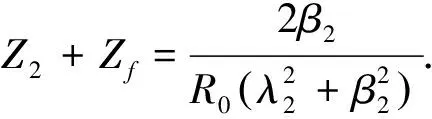
(21)
将式(20)和式(21)并联计算可得
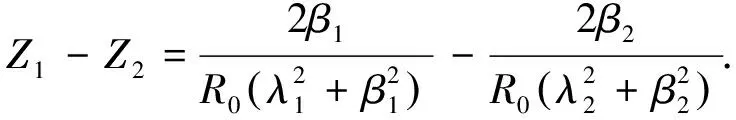
(22)
在整个电力架空线路中,Z1,Z2的数值总和是固定的,二者之和即为线路的总电阻[9]
Z1+Z2=dZunit,
(23)
式中:d为架空线路总长度,在电力线路总长度下的电阻值为Zunit,结合式(22)和式(23),可具体求得电力线路的故障位置以及线路两端的电阻值,并根据电阻值精确判断出线路故障的具体信息。
3 故障可视化运检技术实现
为了使电力架空线路的故障问题可视化,利用检测到的数据汇聚成聚集和离散程度适当的散点图,更清晰地描述运维检测中的故障问题,首先设定ax和bx分别为数据点x与相邻同类别其他数据点之间的距离平均值和最小距离值,以silh作为评估数据离散程度的指标[10],具体表示为

(24)
silh值所属范围在-1到1之间,根据工作人员侧重点合理呈现故障具体信息的内聚和分离,由此可完成电力线路故障检测数据的可视化处理。
4 仿真实验
为验证研究的电力架空线路故障可视化运检技术的性能及有效性,选用一段300 km长的架空电缆线路作为实验对象,进行相应的故障运维检测。并将本文方法与弧光高阻检测法、行波故障检测法的可视化运检结果进行对比,结果如表1 所示。
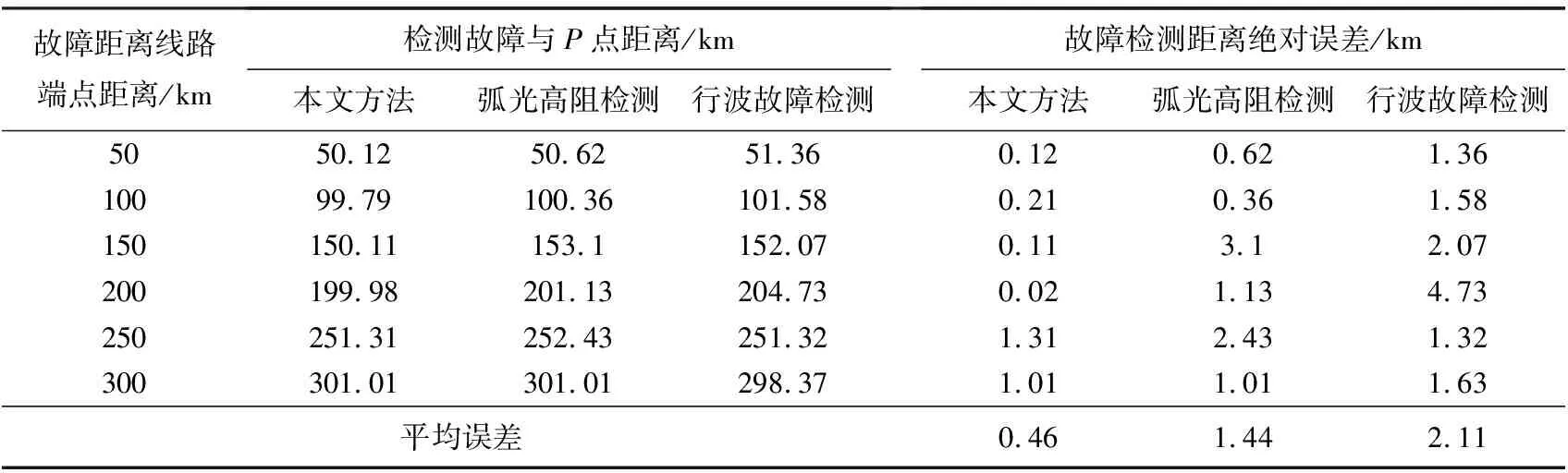
表1 3种方法下架空线路故障运检结果
根据表1 可知,本文方法下所检测的故障发生点与P点距离的测量值较小,绝对误差值保持在0.02 km~0.21 km之间,绝对值的平均误差在0.46。通过仿真实验数据分析,可以证明所提方法可以精确检测到电力架空线路的故障发生位置,故障运检精度高。
针对在线路运检过程中线路故障类型诊断、故障定位检测可能会出现的错误检测或是遗漏检测情况,进行进一步仿真实验分析,对3种运检方法进行多次实验,统计不同方法在对线路运检时存在的错误故障检测率,具体结果如图3 所示。
根据图3 可以看出,本文方法的线路故障运检错误率在2.0%~8.2%之间,相较于弧光高阻检测法和行波故障检测法而言,本文方法在对架空线路进行故障运检时的错误故障检测率低,线路故障类型及定位的检测更加准确,错误情况较少。

图3 3种方法下错误故障检测率
根据图4 可知,本文方法对电力架空线路的故障检测中,遗漏故障检测率与其他量化总方法相比更低,且变化幅度不是很大,可以证明,本文方法能够相对全面地检测线路故障,提高线路安全运检性能。
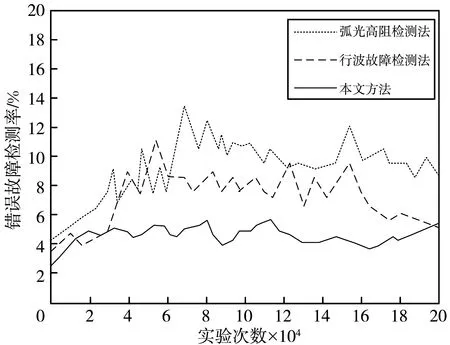
图4 3种方法下遗漏故障检测率
对于电力架空线路的故障检测进行可视化处理,通过仿真实验来验证检测结果可视化的性能效果,将电力线路检测到的稀疏数据应用到Silh值图上,如图5 所示。
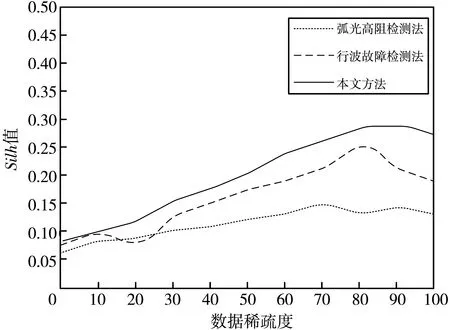
图5 数据稀疏程度与Silh值之间关系变化情况
从图5 可以看出,随着电力线路检测数据的稀疏程度逐渐增加,散点图上Silh值也在随之提高,当数据稀疏程度过大时,Silh值会再次下降,通过对比3种方法的Silh值可以知道,本文方法得到的Silh值相对更大,证明数据的内聚性和分离性都很恰当,改善了数据过于聚集的情况,提高数据分离效果,可视化效果更好,更便于运检人员分析。
5 结 论
对稀疏数据进行特种证提取后,可以挖掘到更深层次的数据信息,在此基础上,对检测到的电力线路数据进行故障分析,可以更快地发现故障位置点,并找到深层次的故障隐患,故障检测效果更加准确,经过将检测数据可视化处理后,更加方便电力运维人员进行数据分析和故障判断,保证可视化运检方法准确有效,误差小,适用性强,鲁棒性好。
