Scratch二分查找算法练习

陈新龙

二分查找（折半查找）是一种效率较高的查找方法，但是二分查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。

假设有1-100的数字，随机选择其中一个数字（假设为63），每次猜测后会对结果判断，提示大还是小。什么方法能保证以最少的次数猜到数字呢？

假设从1开始猜，依次递增1的办法要猜63次。这就是顺序查找算法了，目标数字越大效率越低。

如果使用二分查找，第一次便从50开始猜（100的一半），虽然猜的数字小于目标数字，但是我们已经排除了接近一半的数字；第二次猜75（50-100的一半），虽然猜的数字大于结果，但是我们又排除了剩下数字的一半（75-100）；第三次我们猜63（50-75 的一半）刚刚好是正确答案。

通过对比我们可以发现二分查找很明显要比顺序查找效率高很多。相信你已经看懂二分查找的道理了，接下来小陈老师通过代码给大家梳理一下二分查找的内容。

首先创建一个有序列表用于存放待查询的数组内容（11，22，33，44，55，66），通过询问用户想查找的数值（假设用户想查找数字55），若数值存在则输出结果和数值的位置；若数值不存在，提示数值不存在此列表中。

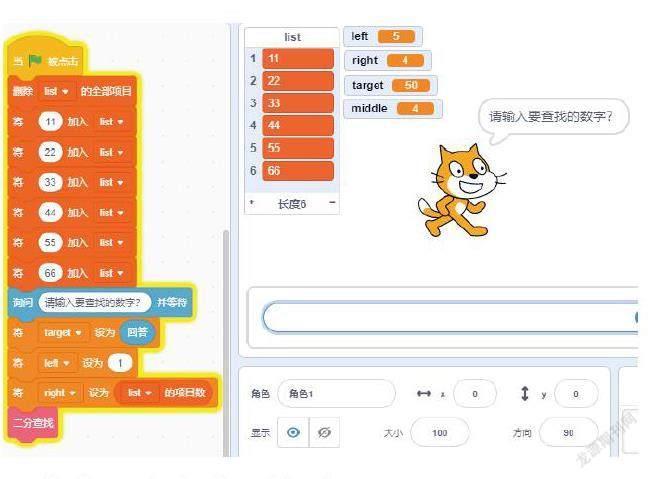
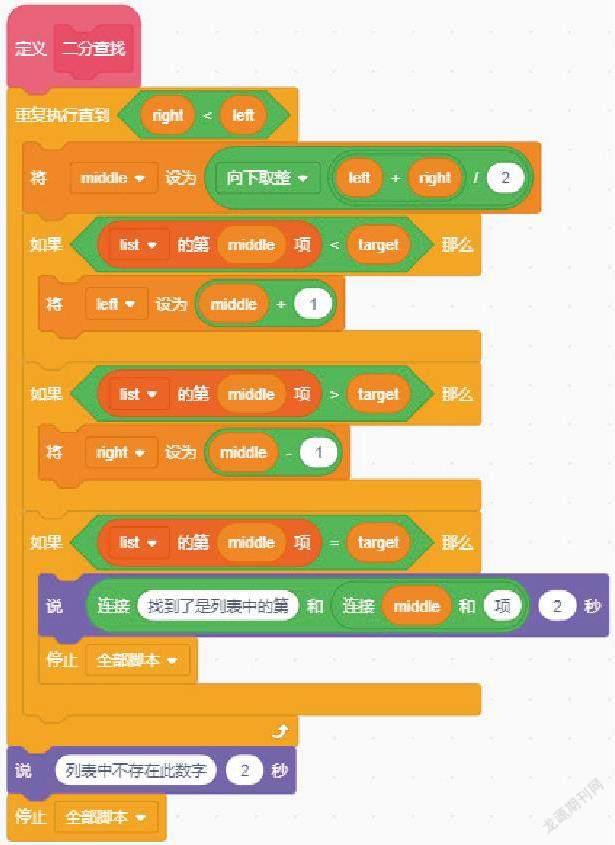
在实现二分查找的过程中我们通过设置变量left 和right 控制一个循环来查找元素（left 和right 相当于我们查找序列的的左边界值和右边界值）。列表中存在六个数，left 和right 分别为1 和6（后续结果中若计算出小数就向下取整），在循环每次迭代的过程中，将middle 设置为left和right 的中间值， 如left=1，right=6的时候，middle 等同于（1+6）/2=3， 也就是3，对应的值为33，很显然33小于55，那么我们便可以排除前三项内容。

将索引值移动到middle 后一个元素的位置上，也就是left = middle+1，right 不變，代表着下一组搜索到的区域便是当前数据集的右半区。如果middle的元素值比目标元素大，那么右索引移动到middle 前一个元素的位置上。也就是right = middle-1，left 不变，代表下一组搜索的区域便是当前数据集的左半区。

我们可以发现一个规律，left 从左向右移动，right 从右向左移动， 一旦middle 所对应的元素是我们需要查找的数字，代表找到目标，查找结束。如果在执行的过程中列表中没有所查找的数字，那么最后结束的标志则是right 小于left。

二分查找算是一种高效的算法，优点是比较次数少，查找速度快，平均性能好，但是也有一定的缺点，要求待查表为有序表，且插入困难，因此二分查找适用于不经常变动而查找频繁的有序列表。