可变斜面光伏清扫机器人行走特性研究
2023-04-03汪步云王伟振汪玉冰
梁 艺,汪步云,全 鹏,孙 凯,王伟振,汪玉冰
(1.安徽工程大学 人工智能学院, 安徽 芜湖 241000; 2.天合光能股份有限公司光伏科学与技术国家重点实验室, 江苏 常州 213031;3.马鞍山学院 人工智能创新学院, 安徽 马鞍山 243100; 4.芜湖安普机器人产业技术研究院, 安徽 芜湖 134000)
1 引言
据文献研究表明,清扫积灰1、2、3天的光伏组件输出功率分别提高3.96%、3.99%、4.01%,以12 MW光伏电站为例,定期清扫后光伏电站经济损失降低了38%[1]。现有的清洗方法中,主要有纳米自清洁薄膜、电帘除尘、人工清洁、喷淋系统、移动清洗车以及清洁机器人。纳米薄膜成本较高;电帘除尘适应于小面积面板且不易除积垢;人工清洗劳动强度大、费用高;喷淋系统用水量大、无法适用缺水地区;移动清洗车无法适用中、小型规模城镇或者家庭适用。集中低成本、高效率、高智能清洁机器人的研制,是世界光伏能源维护运营大国亟待解决的难题。
光伏清扫机器人研究始于21世纪前期[2],文献[3-4]采用的都是移动框架式结构,借助移动导轨较易完成光伏面板定向清洗。由X、Y移动关节简单叠加,组成直角坐标式结构会降低适应性,其自身占用空间较大和运动灵活性欠佳。文献[5-6]采用无框架式结构,这种设计的优势可以实现全场景的路径清扫,更适用于分布式光伏面板、小规模光伏面板清扫,而且不需要用额外移动导轨辅助。但是全向移动式机器人应用在光伏面板清洗上,又出现新的技术难点:大斜面稳定行走机理,动态的清扫路径跟踪技术等问题[7-8]。
近年来光伏支架跟踪技术的应用,以甘肃、青海、新疆和内蒙古等西部省份集中式光伏电站为例,移动式清扫机器人需要在倾斜角30°~60°的表面自适应清扫,不可避免的会与光伏表面产生相对滑动,机器人需要更合适的表面附着能力,尽可能抑制打滑问题[9]。Mori等[10]设计出一种新型的轮子驱动结构避免打滑现象的发生,包含驱动部分和转弯部分。Saha等[11]利用滑动与摩擦系数的关系曲线建立了轮子的动力学模型。Lee等[12]利用模糊控制算法来检测和补偿轮子的打滑。关于机器人运动稳定性问题的研究,周卫华等[13]研究全向轮布局与运动稳定性方法。Nguyen等[14]提出了稳定运动的运动控制器建模以及实现方法,测试的光伏板清扫机器人工作的运动稳定性和轨迹跟踪能力得到了增强。文献[15-16]等研究了机器人的运动与吸附稳定性问题,设计了满足 Lyapunov稳定判据和Barbalat引理的控制规律,并应用到了履带式光伏清洁机器人上。
本文以光伏组件清扫为应用场景,结合文献平面上全向轮布局与稳定性方法[13],针对移动式光伏清扫机器人斜面行走新问题,采用仿真和实验分析,研究机器人在斜面附着特性和速度、力矩综合控制方法,为这类光伏机器人变斜面应用提供技术支撑。
2 行走机构模型
2.1 行走机构设计
如图1所示,光伏跟踪支架工作角度是0°~45°,针对变斜面光伏面板清扫轨迹特点、变斜面稳定行走的严苛要求,移动式清扫机器人结构设计指标如表1所示。

图1 天合光伏跟踪支架场景

表1 设计指标
针对自由度指标参数,移动式清扫机器人实现全向移动,需满足机器人运动学原理,其逆运动学雅克比矩阵列满秩:
(1)
选用多轮驱动组合形式,由轮子与车体中心几何关系如下,获得3种构型方案,如图2所示。

(2)
式中:R为逆运动学雅克比矩阵;l为OOi之间距离;i为轮子的编号;αi为Xi与OX轴夹角;βi为OOi与OX轴夹角。
采用式(1)计算3种构型逆雅克比矩阵的秩,三轮、四轮第二组、六轮第一组构型的各个轮子沿底盘均匀分布,Xi沿底盘中心成圆周切线方向,计算得到逆雅克比矩阵满秩,机器人行走机构都能实现全方位运动;四轮第一组、六轮第二组构型逆雅克比矩阵不满秩,机器人不能旋转或横向移动。由于四轮构型相对于三轮的控制更加复杂且能量消耗更大,六轮构型过于冗余,故行走机构采用三轮第一组构型。

图2 3种构型
对于三轮式全向移动机构轮组结构,采用橡胶轮、履带轮、球轮和正交轮作为轮组,其不易于自锁、原地回转困难。Mecanum轮可以横向滑移、回转,缺点是辊子间隙较大、辊子与地面接触面积小,导致轮组在凸凹表面行走产生振动。双排全向轮结构简单,运动稳定性较好。因此,选择全向轮作为行走机构的驱动轮。假设轮组的附着系数μh为1.0。计算极限情况下驱动轮需要的输出力矩为,
(3)
式中:r为全向轮的半径;n=100表示减速器的减速比;η表示减速器的效率。完成的行走机构设计模型如图3所示。其中清扫模块主要由清扫电机、清扫刷和底座构成,清扫电机选用的是ZGB37RG微型电机,自带1∶24减速器,电压24 V,根据清扫电机和清扫刷的尺寸可以确定底座的尺寸。

1-全向轮组,2-直流伺服电机,3-减速器,4-清扫模块
2.2 行走机构数学模型
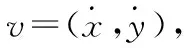
(4)
式中:r为各全向轮半径;ωi为各全向轮角速度;l为行走机构几何中心P点到全向轮的距离。

图4 行走机构力学模型
假设行走机构的总质量m、转动惯量I为常量,电机施加在各全向轮上驱动力为Fi,沿全向轮转动方向摩擦力为FTi、横向方向摩擦力为FLi,根据直流电机方程以及文献[17]测试电机的两个实验参数k1和k2,得到各全向轮的力学模型:
Fi=k1ui-k2vi-FTii=1,2,3
(5)
式中:ui为施加给各全向轮电机的电压;FTi满足-mg/3μTmax≤FTi≤mg/3μTmax,μTmax为全向轮转动方向最大静摩擦系数。
(6)
式中,
f1=FT1sinθ+FT2sin(π/3-θ)-FT3sin(π/3+θ)+
FL1cosθ-FL2cos(π/3-θ)-FL3cos(π/3+θ)
f2=-FT1cosθ+FT2cos(π/3-θ)+FT3cos(π/3+θ)+
FL1sinθ+FL2sin(π/3-θ)-FL3sin(π/3+θ)
结合式(4)、式(5)、式(6),根据牛顿第二平移和旋转定律,建立了行走机构的二阶动力学模型:
(7)

3 机器人行走特性分析
3.1 斜面角φ变化附着特性分析
如图5所示,行走机构在倾斜角为φ光伏面板清扫时,沿全向轮转动方向摩擦力为FTi、横向方向摩擦力为FLi,则用下式计算:

(8)
式中:h表示行走机构中心到全向轮中心的距离;
如图6所示,在Adams仿真环境中建立行走机构动力学模型,完成行走机构静止模式、运动模式下运动性能仿真,设定仿真参数如表2所示。
图7是行走机构静止模式、运动模式下运动性能仿真图。

图5 斜面力学模型
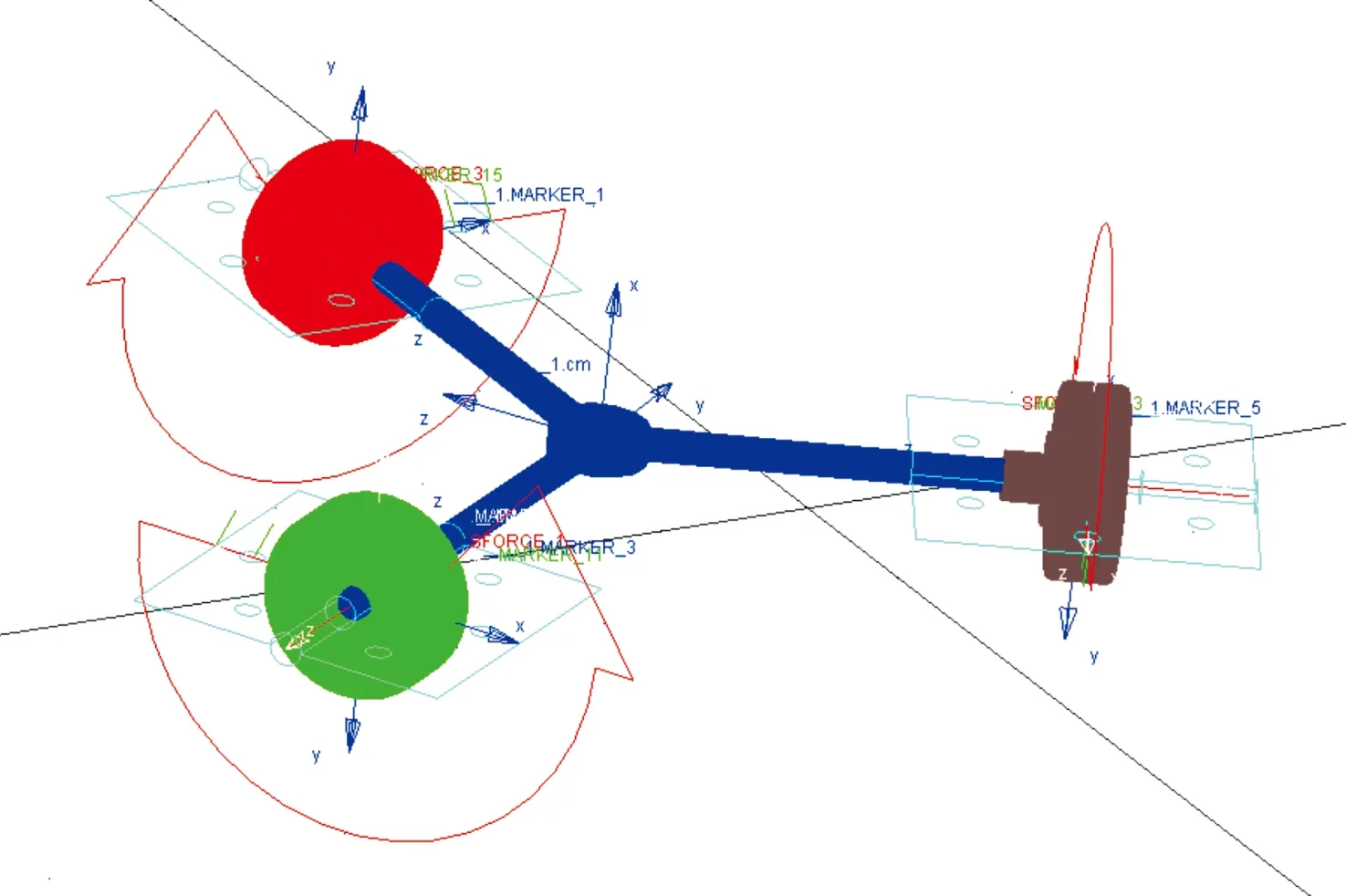
图6 动力学仿真模型

表2 仿真参数
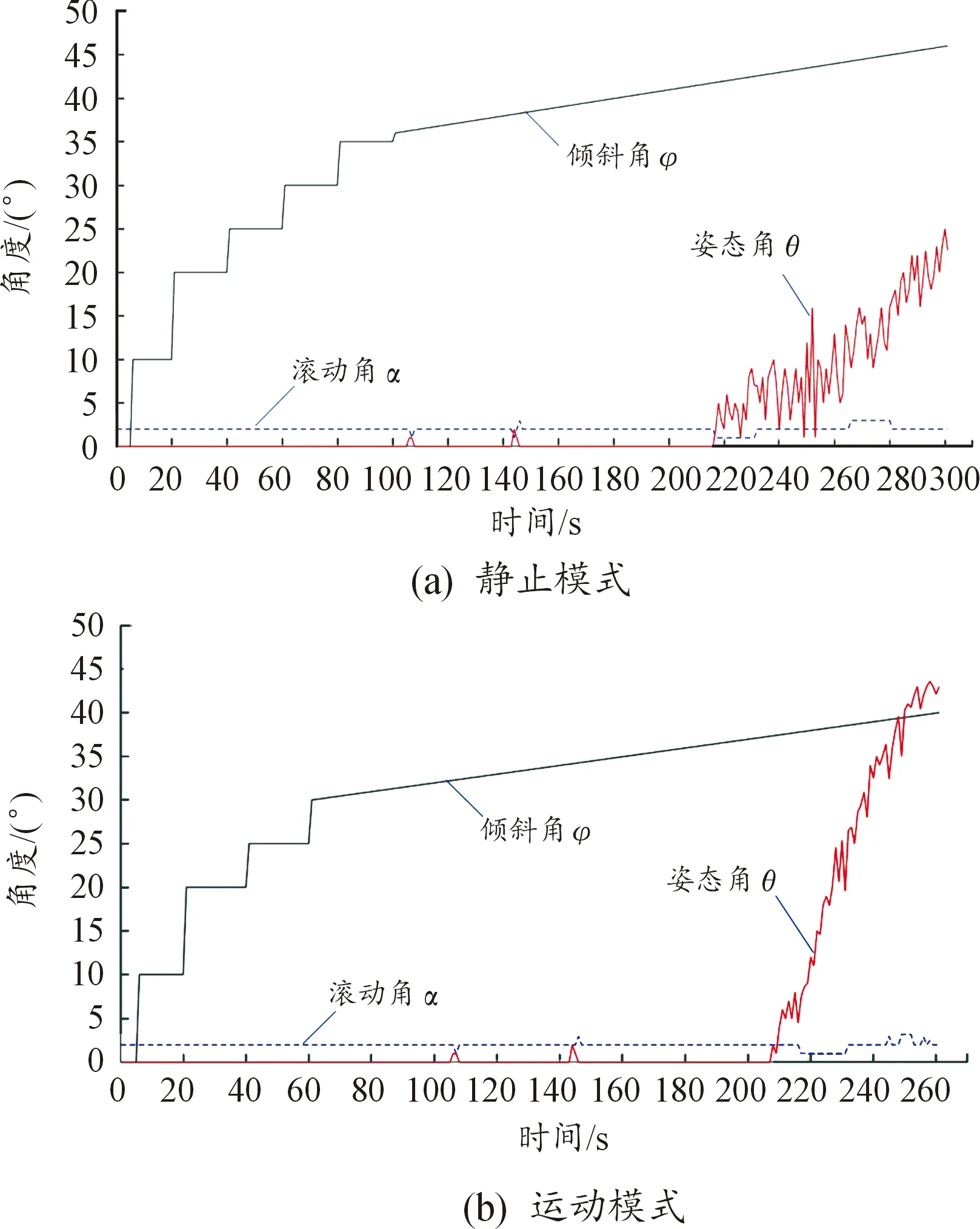
图7 不同模式下行走机构姿态随倾斜角变化图
由图7可知,在静止状态下,当倾斜角φ小于42°时,行走机构的姿态角θ和滚动角α基本处于稳定状态,行走机构在静止状态下自锁角为42°。在运动状态下,当倾斜角φ小于37°时,行走机构的姿态角θ和滚动角α基本处于稳定状态,行走机构在运动状态下自锁角为37°。
3.2 姿态角θ变化速度、力矩分析
当行走机构姿态θ∈(90°,150°)变化时,由运动学模型式(4)、力学模型式(7)、动力学仿真模型,得到3个全向轮的驱动速度和力矩的分布规律。设定全向轮电机额定转速为6 000 r/min,减速比是100,θ为150°时,完成行走机构3个全向轮的速度、力矩分配仿真,如图8所示。
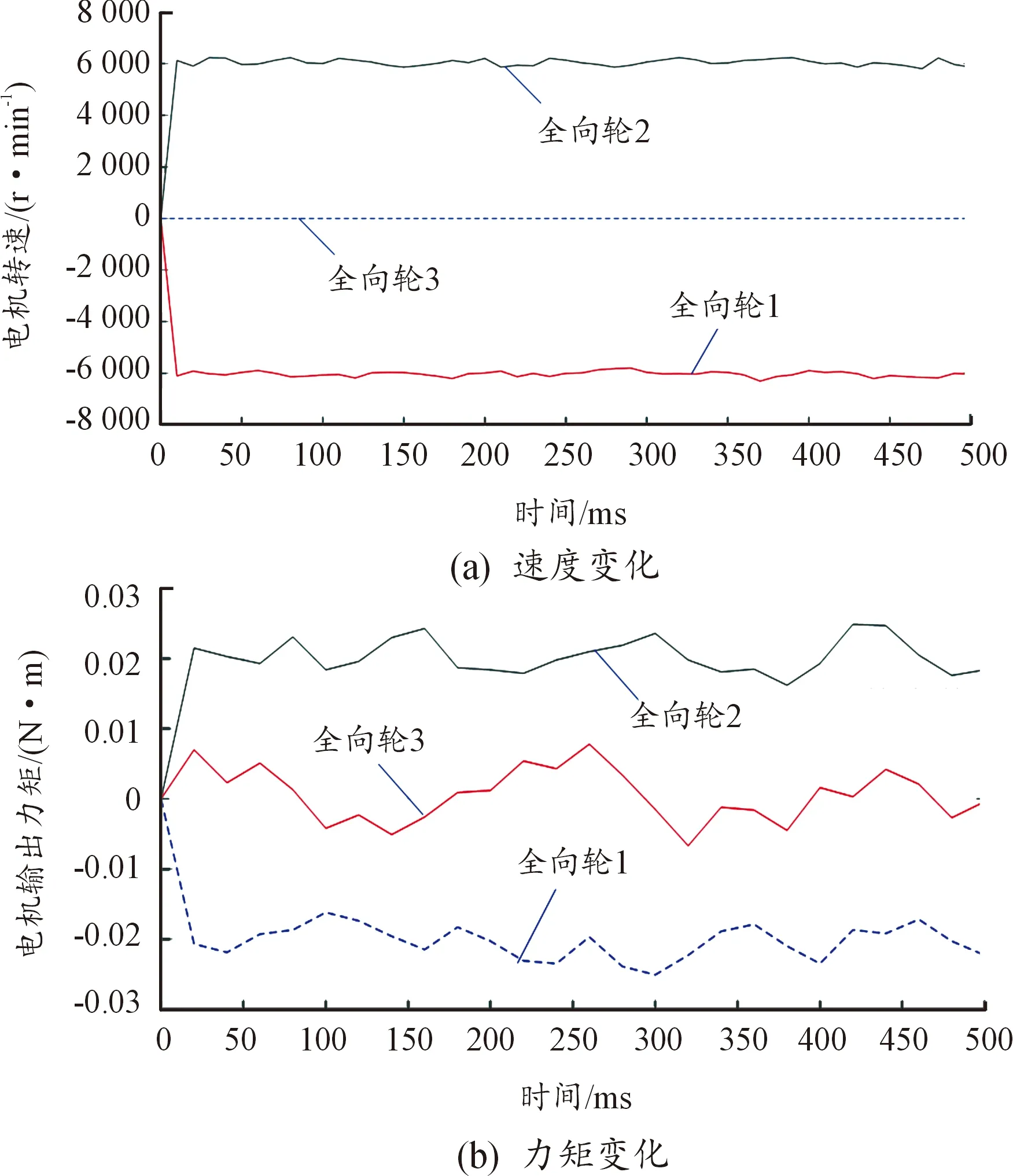
图8 θ=150°时全向轮的速度、力矩分配仿真图
由图8可知,当行走机构以一定的姿态、速度运动时,3个全向轮驱动速度较平稳,而驱动力矩幅值波动较大,这种不规则的力矩分布会使得行走机构在朝着θ方向运动时,3个全向轮之间会出现挤压现象,容易导致各全向轮发生打滑现象,降低了行走机构的稳定性。
4 仿真与实验
4.1 附着特性实验
表3是搭建的智能光伏跟踪支架实验场景数据。完成行走机构在运动模式下的自锁效果测试实验,如图9所示。
图10是行走机构在倾斜角φ∈(0°,45°)依次变化时,由上位机实际测量的3个全向轮驱动电机转速值。由图10可知,在t=205 s,φ=36°之前,驱动电机实际速度跟目标值基本一致,在205 s之后,驱动电机实际速度与目标值出现较大偏差,行走机构处于不稳定状态,行走机构在运动状态下自锁角为36°,实验数据和仿真数据具有较好的一致性。

表3 实验场景数据Table 3 Experimental scene data

图10 各全向轮速度随倾斜角φ变化数据
4.2 速度、力矩双PI控制仿真
为了消除行走机构3个全向轮之间挤压力问题,需要实施行走机构速度、全向轮驱动力矩同步控制[18]。如图11所示。行走机构采用速度、力矩双PI控制策略,速度PI调节时间为2 ms,力矩PI调节时间为10 ms,数字PI调节器的公式为:
uk=uk-1+KpΔek+Kiek
(9)
式中:k为采样次数;uk为第k次输出值;ek为两次采样偏差;Kp为比例系数;Ki为积分系数;Δek=Kp[e(k)-e(k-1)]+Ki*e(k)为两次采样偏差的差值。
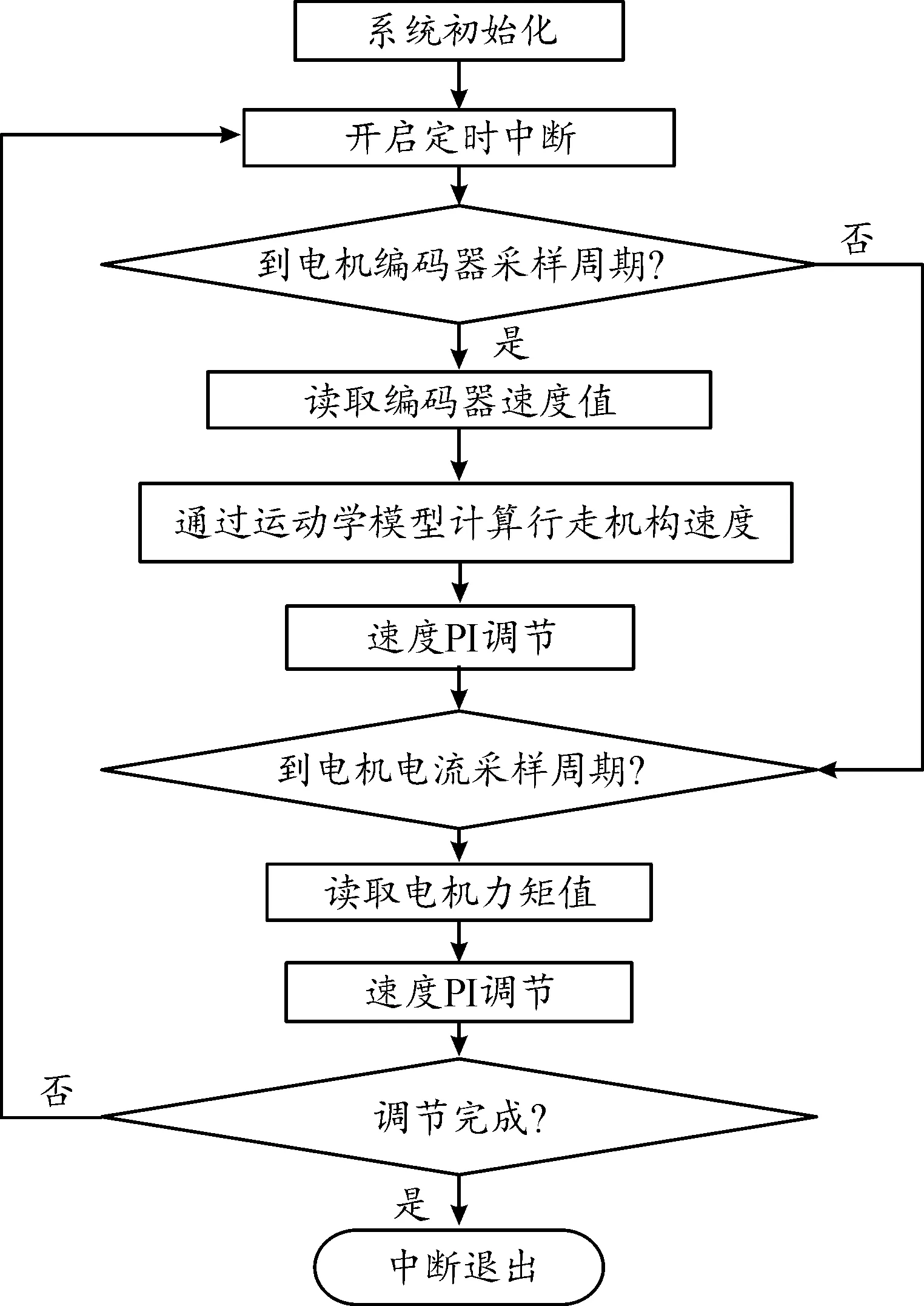
图11 行走机构速度、力矩双PI控制策略
控制策略中全向轮电机速度检测是通过编码器反馈信号,由电机驱动器内部计算,通过CAN总线发送给上位机,行走机构的速度通过运动学模型计算得到,采用数字PI调节器进行速度PI控制。上位机通过CAN总线从驱动器上读取电机的输出力矩值,采用数字PI调节器进行力矩PI调节,参数如表4所示。

表4 PI调节参数Table 4 PI adjustment parameters
当行走机构以0.2 m/s的速度沿θ=90°方向运动时,采用速度单PI控制、速度和力矩双PI控制,分别获得行走机构的速度和电机输出力矩随时间的变化曲线图,如图12、图13所示。计算2种情况下电机输入功率、行走机构实际速度与理论速度的偏差如表5所示。
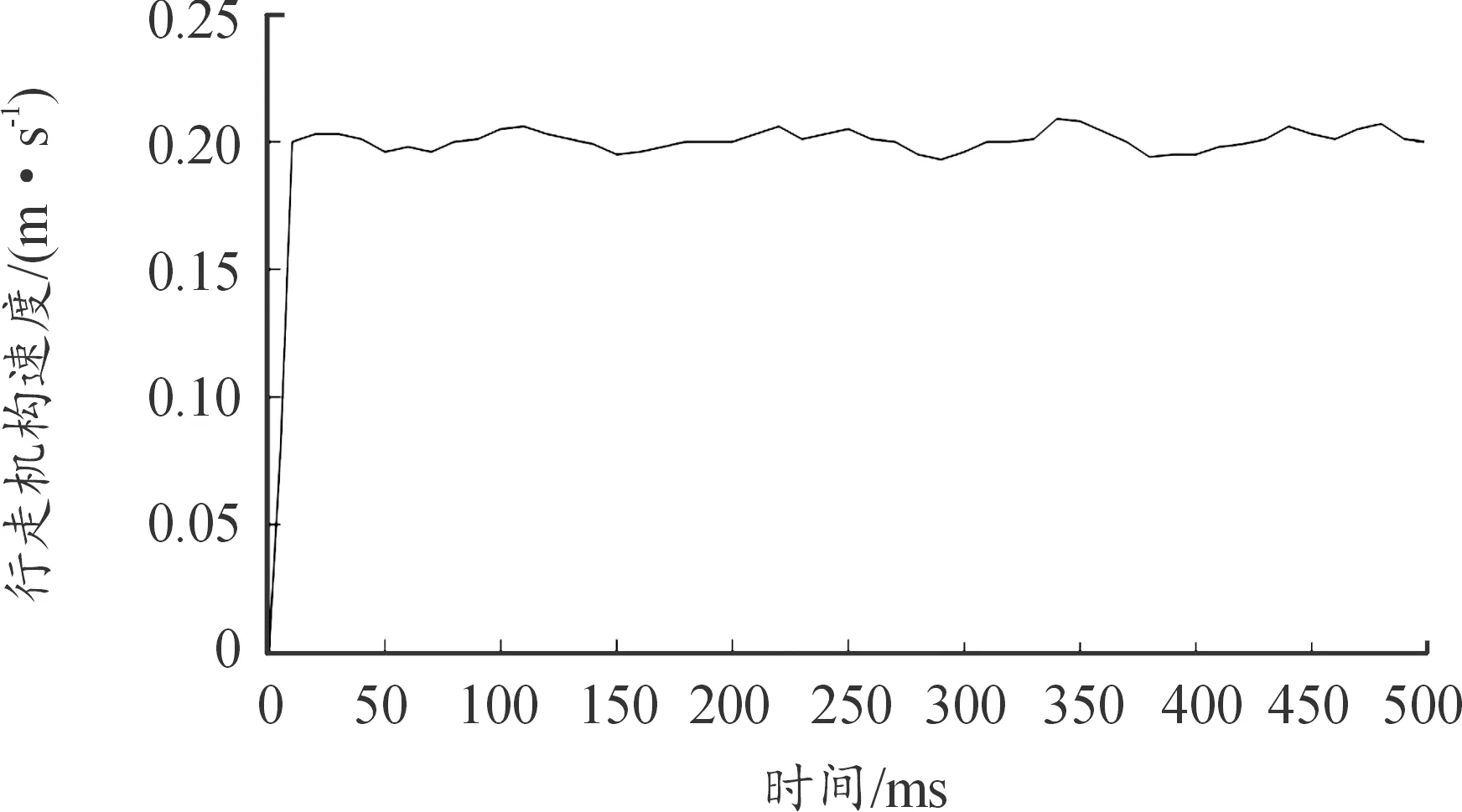
图12 行走机构θ=90°时速度单PI控制仿真图

图13 行走机构θ=90°时速度、力矩双PI控制仿真图

表5 θ=90°电机输入功率、速度偏差
由表5可知,行走机构在θ=90°方向上运动时,单独的速度PI控制下电机的输入功率是31.62 W,而双闭环PI控制下的输入功率是25.72 W,相比速度PI控制,双闭环PI控制的效率提高18.6%。双闭环PI控制下的速度偏差为2.9%,速度PI控制下的速度偏差为4.5%。
5 结论
针对光伏面板清扫特点、大斜面稳定行走的严苛要求,设计了变斜面光伏清扫全向轮式机器人构型,在建立其数学模型基础上,完成了机器人行走特性分析和实验,得到如下结论:
1) 通过斜面角φ变化附着特性仿真和实验,在满足本文动力学模型式(7)、摩擦力模型(8)前提下,三全向轮式对称构型,在斜面上有一定附着角度,在给定静摩擦系数μTmax、μLmax、m等条件,仿真和实验验证了该行走机构在静止状态下自锁角为42°,运动状态下自锁角为36°左右。
2) 通过姿态角θ变化速度、力矩分析和仿真,行走机构以一定的姿态、速度运动时,3个全向轮驱动速度较平稳,而驱动力矩幅值波动较大,轮组间会出现挤压现象。针对全向轮之间挤压力问题,通过速度、力矩双PI控制仿真验证,行走机构在一定姿态θ方向上运动时,双闭环PI控制的功率、速度偏差,相比速度PI控制,控制效果有了一定提高。
