“打折销售”话学生阅读能力培养

●董永春

近年来，各地中考试题中生活化的真实情境增多，对学生阅读能力的考查明显增强。邵光华认为，数学阅读过程同一般阅读过程一样,包括语言符号(文字、符号、图表等）的感知和认读，新概念的同化和顺应，阅读材料的理解和记忆等各种心理活动因素[1]。苏霍林斯基说过：“凡是没有学会交流地、有理解地阅读的人，他是不可能顺利地掌握知识的。”[2]

一、课例分析

笔者有幸参加四川省国培“烛光计划”，对乡村教师执教了“打折销售”一课，这节课属于七年级上册第五章一元一次方程单元。方程是数学的核心知识，教材依次从一元一次方程、二元一次方程、分式方程、一元二次方程螺旋式呈现。笔者力争实施逆向教学设计，以一元一次方程为一个大概念来设计教学，以真实问题情境为切入点。所谓逆向教学设计是由美国的威金斯和迈克泰提出的，他们将教学的逆向设计过程分为三个阶段：“确定预期结果→确定合适的评估证据→设计学习体验和教学”[3]。开始上课时，教师抛给学生一个完整的打折销售问题，用这个既有难度又有挑战性的问题激发学生主动探索的欲望，教师在整个教学过程中作为引领者，学生真正成为学习探究的主体，学生在应用题解决的过程中习得数学知识并且使阅读能力得到发展。现选取课堂几个教学片段，以供读者研讨。

二、教学过程

片段一：创设生活情境问题，引出研究内容

问题：国庆期间，老师在春熙路逛街时买了一件衣服，告诉同学们如下信息，你能知道这件服装每件的成本价是多少元吗？这件衣服是按成本价提高40%后标价的，又以8 折优惠卖出，结果商家每件仍获利15 元。你能从中得到哪些与销售有关的量？

设计意图：从学生身边的真实问题引入，让学生体会到数学是能解决身边真实问题的有用的学科，引导学生从真实问题情境中去掉情境化表述，剥离出具体的数学模型，分析问题，找到相应的等量关系并解决问题，这是整节课的主线。学生解决这个应用题所经历的步骤，也是解决其他类型应用题的一般步骤，这个方法具有普适性，因而这个步骤就是一个学科的大概念，可为学生后续学习类似的方程问题积累经验，让学生“一滴水里见太阳”，而不是就题解题。

点评：上课一开始就把这个问题完整地抛给学生，就是逆向教学设计，学生可能暂时无法解决这个问题，也不具备解决这个问题所需的知识，这个问题对学生来说就是一个挑战性的问题，学生为了解决这个问题，就需要主动学习相应的知识，学生的内驱力得到激发。

片段二：引领学生读题，厘清等量关系，分解问题

想一想：设每件服装的成本为x 元，你能用含x 的代数式表示其他的量吗？问题中有怎样的等量关系？

(1)每件服装的标价为：（1+40%）x 元；

(2)每件服装的实际售价为：1.4x·80%元；

(3)每件服装的利润为：（1.4x·80%-x）元；

由此，列出方程：1.4x·80%-x=15。

解方程，得x=125 元；

因此每件服装的成本价是125 元

设计意图：通常情况下初一学生的语言文字阅读理解能力不强，不能对各种信息和数据进行准确加工处理。学生前面学习了字母表示数，了解到字母可以参与计算，用未知数表示更多有关联的变量变得可能，可用数学的符号语言表达等量关系。教师要引导学生学会思考，学会分解问题，分析题干中的内容涉及哪些数学的量，准确地把握这些量并有条理地表达出来，进而理清他们之间的等量关系，建立方程，解决问题。

点评：列方程解决实际问题的关键是什么呢？是找到等量关系。学生用数学的眼光阅读材料，并对信息进行处理和加工，体现学生的数学应用意识，将实际问题抽象出数学模型是应用题学习的难点。学生在加工信息和问题分解的过程中学习能力得到发展，数学思维得到锻炼，解决问题的能力得到增强。

片段三：独立问题解决，学会迁移应用，发展能力

例1：成都王府井商场将某种商品按原价的8折出售，此时商品的利润率是10%。此商品的进价为1800 元，那么这种商品的原价是多少[4]？

生1：设商品原价是x 元，根据题意得80%x=1800(1+10%),解得x=2475，

因此每件服装的原价是2475 元。

生2：由小学所学内容知，原价为：1800(1+10%)80%=2475。

设计意图：利润率是打折销售类应用题的一个关键量，即利润率=（利润/成本）100%，抓住这个等量关系是关键，这里的“进价”就是“成本”。学生通过前面一个问题的解决，初步经历如何理清题目中的量，如何找到等量关系并建立方程，体会列方程解应用题的数学思想与方法，感受到方程解决的模型思想，也积累了解决问题的经验。

点评：阅读是一种智力技能，语言的学习是离不开阅读的，合理控制阅读进程，提高数学阅读水平是学生终身发展的需要。应帮助学生学会阅读应用题，引导学生认真读题，圈出关键量和数字信息，学会重组和加工碎片信息，抓住所属应用题类型的等量关系，有条理地表达出相应的量，培养学生的建模意识。

随堂练习：一件夹克按成本价提高50%后标价，后因季节关系按标价的8 折出售，每件以60 元卖出。这批夹克每件的成本价是多少元？

生3：设这批夹克每件的成本价是x 元，根据题意得(1+50%)0.8x=60,解得x=50，

因此这批夹克每件的成本价是50 元。

生4：由小学所学内容知，原价为：60[(1+50%)0.8]=50。

设计意图：根据七年级学生数学思维水平，模仿训练很有必要，学生在再次实践问题解决的过程中，熟练了此类应用题的解题步骤，深刻体会方程解应用题就是一种模型化、程序化的建模过程，小学的思维是根据题意倒推计算出答案，是从具体问题的已知数出发正面计算的思维方式，方程的思维是逆向的过程，学生能逐步感受到方程解决复杂问题的优越性。

点评：对于一些基础且重要的数学知识，浅层的重复学习是必要的，新课程改革关注单元教学，倡导更多关注知识间的关联性，指向的是深度学习，但也没有排斥浅层学习，适量且恰当的练习对数学学习很有必要。培养学生的符号意识，小学的算术思维讲的是一个故事，而方程讲的是两个故事，列方程解应用题发展了学生的高阶思维。

片段四：总结学习内容，增强知识间的关联性

（1）感受方程是刻画现实生活中等量关系的有效模型，列方程解决实际问题的关键是找到等量关系。

（2）列方程解决实际问题的核心思想为：

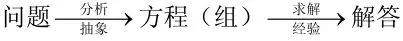
（3）一般步骤：审、设、列、解、检、答。

设计意图：这部分可以请部分学生总结并分享，课堂小结时很多教师担心学生会出现总结不全面的情况，其实学生没有总结到的教师及时补充和强调即可；也有一些老师总结就是走形式，没有对这节课的中心思想和数学方法进行提炼。学生从上课开始的问题提出，到逐步表达出关键量，找到并建立等量关系，列方程解答，经历了完整的应用题解题过程，通过一系列的问题解决已经对本节课的方法有了较为深刻的理解，在本节课结束之时，引导学生回到方法产生的本源，感受数学方法的普适，体会数学思想方法的广泛运用，可为后续的学习打牢基础。

点评：教师进教室的任务不是去“教”学生，而是组织学生“学”，教师要成为课堂的引领者和组织者，引导学生重视在数学思想方法的指导下对题目进行总结和归纳，注重课本内容的归纳整理，培养自学能力；学生要有归纳和迁移的意识，逐渐形成透过现象看到本质的能力，长此以往定能提高数学思维水平与解题能力。

三、教学反思

（一）注重模型解题，渗透建模思想

孔凡哲教授认为方程思想的核心为模型思想和化归思想。应用题解决的关键是阅读、建模、计算，能够准确地列出方程是解决应用题的必要条件。教师要通过精心设置情景相对复杂的挑战性问题，留足时间让学生独立解决问题，学生在经历完整解决问题的过程中积累经验，有助于数学建模能力的发展，引导学生形成数学意识，能用基本数学知识和基本方法解决实际问题，是近几年教育界达成的共识。通过解决相似性问题的联想，得到解决一类问题的普适方法，以有限的数学模型解决一般模型问题。教师应从已有知识经验和认知特点出发向学生渗透模型思想，同时，教学中不应过分强调题目类型，学生解决问题不能仅靠生活经验，必须上升到理论层面，体验数学建模的步骤，促进方程知识的连贯性学习，提高学生的学力。

（二）注重阅读力培养，形成关键能力

顾明远认为阅读是一种从书面材料获得意义的心理过程，也是一种基本的智力技能，是取得学习成功的先决条件[5]。阅读是以理解为核心的认知活动，教师要教会学生善于运用纸笔演算等辅助阅读，从文本的获得力、符号的解码力、信息的理解力、文稿的驾驭力、内容的批判力、情景的感受力、再现的表达力、审美的构建力[6]等方面培养学生的阅读能力。教师应切实转变知识本位的教学方式，不再是带着学生解决单一问题，现实中学生往往遇到的是复杂的而非单一的问题，学生遇到的是劣序的而非良序的问题。应给足学生阅读的时间，教会学生阅读的方法，真正关注到学生关键能力的培养。

（三）注重逆向设计，培育核心素养

逆向设计关注“学生最终学到什么”，是以大概念、大主题为线索，贯穿教学的始终，以驱动性问题激发学生的内驱力。逆向设计需要教师整体把握教学的核心知识，比如这节课对学生最困难的是什么，这节课对学生有什么用途，这节课对教师来说苦恼的地方在哪里，等等。学校应加强组内的集体备课质量，集体进行教材解读，充分了解学生的需求，教师清楚了这些问题，才可能精心设计问题，引导学生在解决一系列问题中学到知识，让数学学科素养得到发展。

逆向设计是一种理念，把“学”摆在了教学设计的核心位置，真正践行学生为主体的教学，传统教学中的“猫论”要不得，以往的知识本位的教学要打破，教师也不能只关注“分数”。教师应实施单元整体教学，以终为始更多地关注学生学习能力的培养，以阅读能力的培养为着力点，实现学生的全面发展。