基于数值模拟的地铁冷凝通风空调系统运行优化研究

付智杰

（中铁第一勘察设计院集团有限公司 西安 710043）

0 引言

随着社会经济的进步与发展，我国城市现代化发展速度迅猛，公共交通等基础设施建设量不断增加，公共交通的便利性大大提升[1]。并且在全球气候与环境问题日益突出的生态背景下，安全性高且污染较小的公共交通工具逐渐成为人们的日常出行交通方式[2,3]。地铁作为城市公共交通系统的重要组成部分，运载量较高且快速便捷，在众多城市得到了快速发展。但是地铁系统的运营能耗较高是制约地铁发展的重要影响因素，而地铁的空调系统能耗在非牵引能源消耗中的占比超过一半，要求在满足地铁运行需求和人员舒适性的条件下，降低地铁的运营能耗[4,5]。因此，研究为了地铁冷凝通风制冷空调系统的能源消耗，通过数值模拟的方式，提出地铁空调系统的低能耗运行优化模型，期望进一步提升地铁空调系统的节能性。

1 数值模拟下的地铁冷凝空调系统运行优化

1.1 地铁冷凝空调系统建模

对地铁冷凝空调系统进行分析，首先对地铁冷凝空调系统进行数学建模，求解空调系统在不同空气、负荷参数下的总功率，为地铁空调系统运行优化提供参考。空调系统的压缩机是制冷的重要部件，通过对制冷剂进行挤压操作，促使制冷剂的流动和形态变化[6,7]。研究结合制冷机状态参数、排气量等参数构建压缩机的效率模型，并将压缩运行过程近似转换为热力学多变过程。在考虑电机损失的情况下，空调系统压缩机的功率如式（1）所示。

式（1）中，Wcom表示压缩机的指示功率，ηei为电机效率，Ws为压缩机运行过程中制冷剂等熵压缩的做功，ηs表示等熵效率，mη和ηmo分别为压缩机机械效率和电机效率。

空调系统蒸发器分为两区，制冷剂在两相沸腾区从两相状态蒸发转为饱和气体，然后在过热蒸汽区经过加热变为热蒸汽[8,9]。因此研究采用分布参数法构建蒸发器模型，将两区按照不同的标准分别划分为若干微元体，两相区以制冷剂的焓差变化为标准，而过热区则以制冷剂的温度变化为标准。在蒸发器建模过程中，不考虑管内制冷剂的径向流动，而将其视为一维流动过程，不考虑管道的轴向导热问题，并且假设管道内制冷剂分布处于均匀状态。蒸发器空气侧的传热和传质方程如式（2）所示。

式（2）中，Qe,a表示空气侧的热换量，me,a表示蒸发侧的空气质量流量，he,a,in和he,a,out分别表示各个微元部分的进风和出风空气焓值，We,a表示微元段的平均空气含湿量，dh为传质系数，d表示微分，Ae,a表示空气侧的换热面积。

建立空调系统蒸发式冷凝器的分布参数模型，依据相态变化将冷凝器分为过热区、两相区和过冷区，过热蒸汽在过热区冷凝为饱和气体，然后在两相区冷凝为饱和液体，在过冷区进一步降温最终进入节流阀。为了便于建模，不考虑流体的热传导和管壁轴向导热，不考虑水平管的重力条件，并且在两相区分析中使用平均空泡系数模型，平均空泡系数不发生变化。管道内部制冷剂与水膜的换热方程如式（3）所示。

式（3）中，mr表示制冷剂的质量流量，hc,r表示微元部分的制冷剂的平均焓值，aw表示传热系数，Ac表示制冷剂侧的换热面积，Δtc,r-w表示冷凝温度与水膜的温度差。水膜与空气之间的传热方程如式（4）所示。

式（4）中，aj表示当量换热系数，Δtw-c,w,a为水膜与空气的温度差，Δhc,w,s-c,a表示水膜表面饱和湿空气与空气之前的焓差。

从空调系统风机的设备数据信息中获得风机特性曲线，结合地铁送风系统管网的特性曲线求解风机工况点，风机全压如式（5）所示。

式（5）中，Qf表示风量，a、b、c均为常数。风机的轴功率计算函数如式（6）所示。

式（6）中，fη表示风机全效率。风机电动机功率如式（7）所示。

式（7）中，K表示储备系数，dη表示电动机效率。

顺序模块法和方程求解法是仿真系统求解的常用方法，顺序模块法以系统的构成结构与特点为基础，将按照一定的顺序将系统各个模块构建成一个系统模型，在假定初值后，从内层模块开始对模型变量进行计算，直到达到收敛条件[10,11]。相较于方程求解法，顺序模块法的求解步骤清晰，并且调试难度较小，便于较快发现问题所在。因此研究采用顺序模块法求解制冷空调系统的模型，空调系统模型的计算求解流程如图1所示。输入系统模型的已知部件参数，并假定系统的蒸发、冷凝温度和供水温度，分别通过系统模型中的压缩机、冷凝器等模块计算地铁冷凝空调系统的运行参数情况。

图1 空调系统模型的计算求解流程Fig.1 Calculation and solution process of air conditioning system model

1.2 空调系统运行优化设计

研究以空调系统的数学模型分析为基础，在约束条件下计算空调系统在不同运行工况下的系统能耗，并提出地铁冷凝空调系统的运行优化模型，在保证系统效果的同时降低能耗。通过对空调系统设备的运行频率下降控制，达到降低系统总能耗的目的，由于喷淋水泵在总能耗中的占比较小，而蒸发器侧和冷凝侧风机与压缩机占比较大，因此以这三个设备的功率构建空调系统运行优化的目标函数，目标函数如式（8）所示。

式（8）中，Wzsf、Wfjp和WY分别表示蒸发器侧风机、冷凝侧风机与压缩机的运行功率。系统运行优化需要以保证制冷量为前提，并且需要满足系统的冷凝压力条件和蒸发压力条件。系统冷凝压力，过高的冷凝压力可能会导致制冷剂泄漏的问题，而过低的冷凝压力会使得制冷量大幅下降，影响空调系统的制冷效果。蒸发温度过高和过低都会引发压缩机过载的问题，导致除湿效果降低或蒸发器结霜，因此需要保证系统的蒸发压力保持在合理范围内[12]。地铁的冷凝空调系统除了控制室内温度，还需要进行通风送风，因此需要保证系统的新风量满足需求。以GB 157-2013 地铁设计规范中的人均新风量要求为标准，设置系统优化的送风量条件。空调系统运行优化的约束条件如式（9）所示。

式（9）中，eQ表示制冷量，Pc表示冷凝压力，Pe表示蒸发压力，G表示送风量，nr表示停站瞬时人数。在建立的空调系统数学模型中输入压缩机频率、蒸发器侧和冷凝侧风机频率、室内冷负荷等工况参数，计算空调系统设备的运行功率和蒸发冷凝条件数据。通过计算空调系统在不同运行工况下的系统总能耗，并结合约束条件加以筛选，获取系统总能耗最低情况下的各个设备运行频率，建立地铁冷凝空调系统的运行优化模型。由于地铁站所需制冷量在实际运行过程中，难以进行实时准确预测，因此将运行优化模型与地铁自控系统相结合，利用回风温度对压缩机进行调节，并结合冷凝温度对风机进行调节，空调系统运行优化自适应控制流程如图2所示。

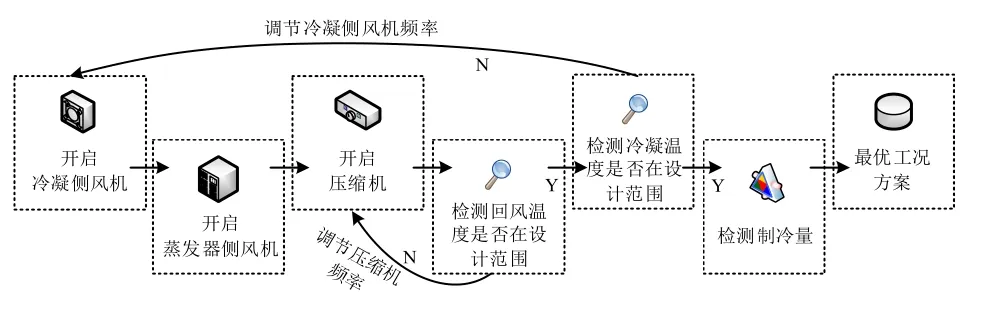
图2 空调系统运行优化自适应控制流程Fig.2 Adaptive control flow optimized for air conditioning system operation

2 空调系统运行优化效果分析

2.1 空调系统模型验证

研究从某市随机抽取20 个地铁站制冷空调系统，采集地铁站2019-2021年制冷季的历史数据创建数据集，并从中选取35 个典型工况作为测试工况，对研究模型进行验证分析。该市位于温带季风气候区，随机抽取的20 个地铁站的平均建筑面积为18344.67m2，高峰期平均人流量为3658.29 人/h，平峰期平均人流量为1106.54 人/h，平均新风湿球温度为22.6℃，平均制冷量为798.6kW。35 个测试工况的参数如表1所示。

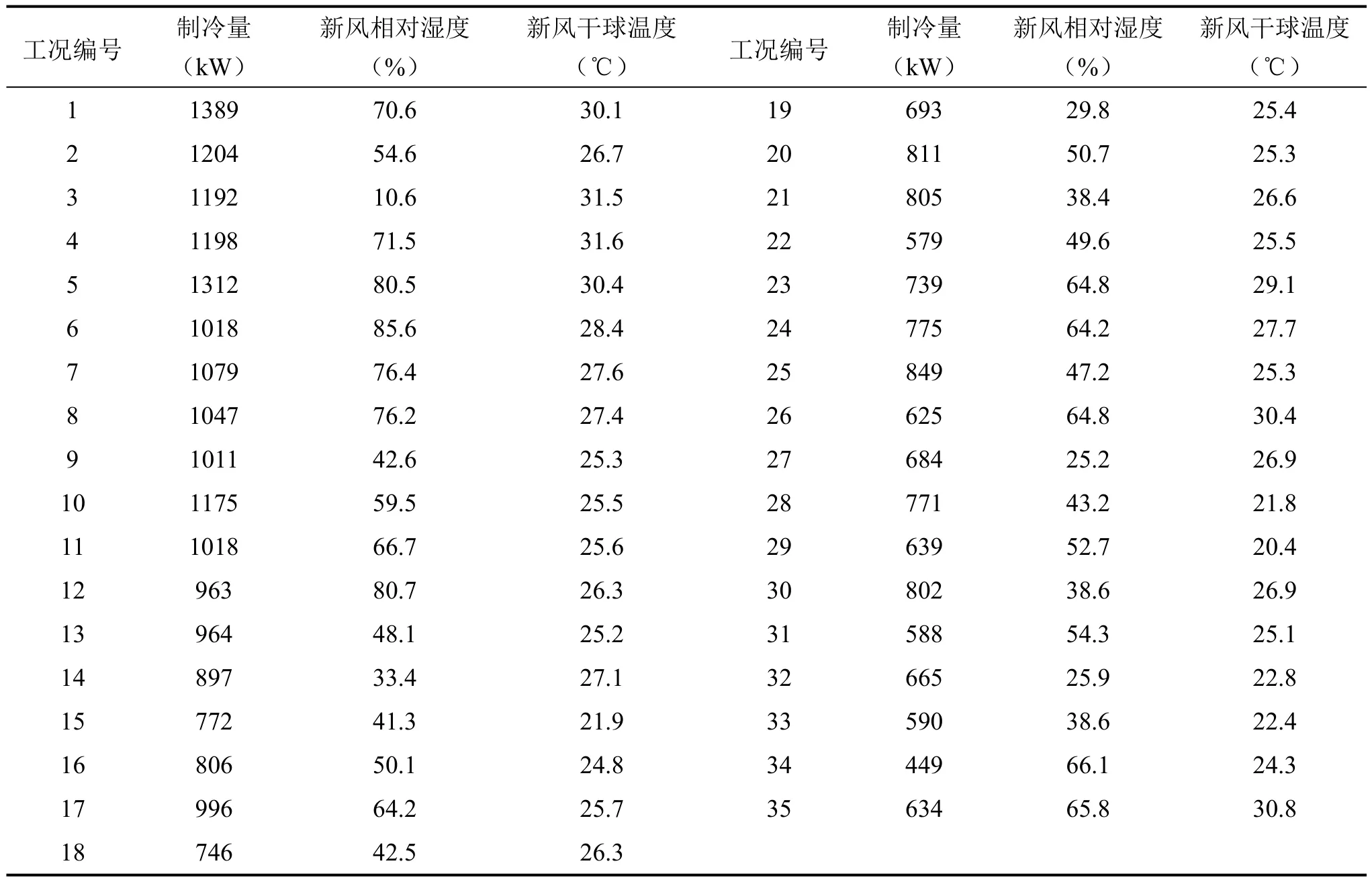
表1 35 个测试工况参数Table 1 35 test condition parameters

对模型在35 个测试工况下的仿真模拟效果进行分析，不同工况下的模型压缩机功率和制冷量误差情况如图3所示。

图3 不同工况下的模型压缩机功率和制冷量误差情况Fig.3 Model compressor power and cooling capacity errors under different operating conditions

从图3中可以看出，在不同的室内情况与室内制冷负荷条件下，模型的压缩机功率仿真值与地铁站实际值的差值较小，仿真误差均保持在±10%以内，满足工程设计计算的误差要求。而从制冷量仿真值上看，研究所构建的模型制冷量仿真值与制冷实际量之间的误差也均未超过10%，符合工程计算标准，证明研究模型能较好对地铁站空调系统进行仿真模拟。为了保证系统运行优化模型的准确性，需要对模型的蒸发温度和冷凝温度进行验证，由于蒸发和冷凝温度难以直接进行测量，因此研究从模型的吸排气温度进行对比验证，模型吸排气温度误差对比情况如图4所示。

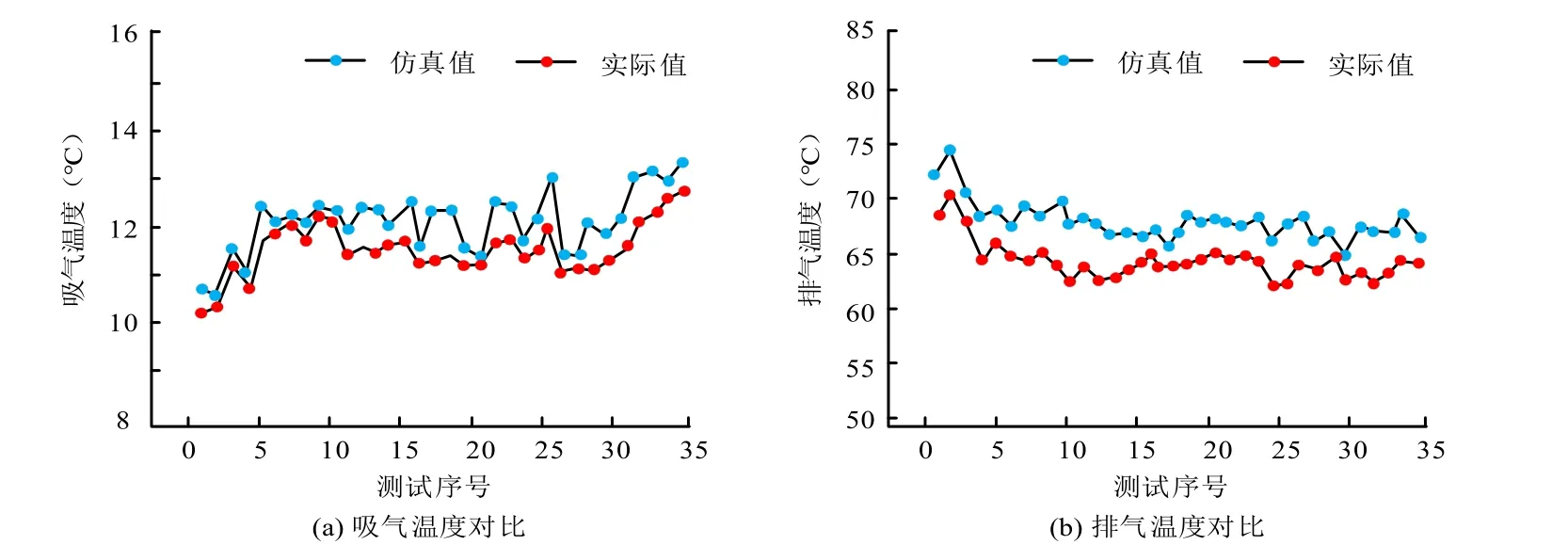
图4 模型吸排气温度误差对比情况Fig.4 Comparison of model suction and exhaust temperature errors

从图4（a）中可以看出，模型的吸气温度仿真值与实际温度之间的误差值较小，差值均小于1℃，出现误差的原因可能是膨胀阀的开度较小导致过热度偏高，高于设定值，使得最终吸气温度略高于实际值。从图4（b）中可以看出，模型排气温度仿真值与实际值的误差范围不超过10%，平均仿真误差值为3.26±1.42℃，满足模型设计要求。由于压缩机的排气口无法直接布点进行数据采集，而将测试点布置在冷凝器，与压缩机之间存在一定的距离，导致排气温度出现测试误差。

2.2 运行优化效果分析

为了分析运行优化方对地铁空调系统的实际优化效果，以地铁站历年数据中的最高制冷负荷情况为实验工况，分析运行优化模型在实际地铁制冷系统上的应用效果。根据历年数据统计，地铁站的最大制冷量为959kW，对应参数如表2所示。

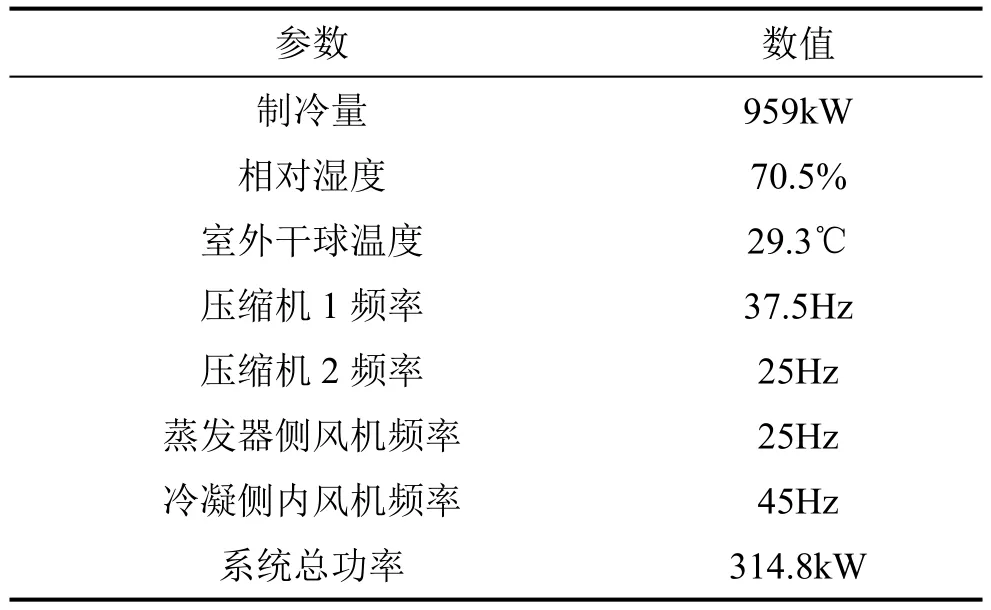
表2 工况参数Table 2 Operating parameters

在最高制冷负荷工况下，使用研究所提出的运行优化模型分析最优工况点，剔除数据中制冷量不满足要求、冷凝温度过高、蒸发温度过低等不符合约束条件的数据，蒸发器侧风机频率和冷凝侧风机频率对系统总功率的影响情况如图5所示。

图5 蒸发器侧风机频率和冷凝侧风机频率对系统总功率的影响情况Fig.5 The influence of evaporator sidewind frequency and condensation sidewinder frequency on the total power of the system

从图5中可以看出，随着蒸发器侧风机和冷凝侧风机频率的增加，系统总功率呈现出先减小后增加的趋势，地铁站的冷侧风机为送风机，送风机频率的增大使得风量增加，降低了压缩机的功率，导致系统总能耗下降。当蒸发器侧风机频率在20-30Hz 范围内，冷凝侧风机频率在25-35Hz 范围时，系统总功率最低。但是冷凝温度偏高存在制冷剂泄漏的风险，因此选择蒸发器侧风机频率25Hz，冷凝侧风机频率30Hz 为最佳工况点，此时系统总功率为277.5kW，相较于历史数据降低了37.3kW，减少了系统总能耗。为了验证运行优化模型的适用性和有效性，对来自20 个地铁站历史数据的35 个典型工况进行运行优化验证，原始工况和优化工况的对比结果如图6所示。

图6 原始工况和优化工况的对比结果Fig.6 Comparison results of the original and optimized conditions

从图6中可以看出，经过优化调整，优化工况下制冷系统的总能耗相较于原始工况均有所降低，总能耗降幅在8.7%-23.6%范围内，降幅最大工况为测试工况6，测试工况6 的原始能耗为254kW，而优化后系统总能耗为195kW，降低了59kW，能耗降幅为23.6%。降幅最小工况为测试工况23，工况23 的原始能耗为183kW，优化后能耗降为167kW，降低了16kW，降幅为8.7%。结果证明研究所提出的运行优化模型能有效降低制冷系统的总功率，能适用于不同运行条件下的地铁空调系统，对降低地铁站冷凝通风系统的能源消耗具有重要价值。

3 结论

为了提升地铁冷凝通风制冷空调系统的节能性，研究结合分布参数法和顺序模块法建立空调系统的数学模型，并进行求解，对空调系统的运行参数情况进行深入分析，建立空调系统的节能运行优化模型，提出地铁冷凝通风制冷空调系统的自适应运行优化模型。实验结果表明，研究所构建的模型制冷量仿真值与制冷实际量之间的误差也均未超过10%，符合工程计算标准。模型吸气温度仿真误差均小于1℃，排气温度仿真误差范围不超过10%，平均仿真误差值为3.26±1.42℃，满足模型设计要求。经过优化调整，优化工况下制冷系统的总能耗降幅在8.7%-23.6%范围内，能有效降低制冷系统的总能源消耗，提升空调系统的环保性和节能性。未来可以在数值模拟的基础上，引入深度学习技术对历史数据进行深入挖掘，建立前馈预测系统，实现对地铁空调系统的预调节。