基于AGNN舆情指数网络的价格指数预测研究

曹 雷 尚 维 谢士尧 王 向

(1.中国科学院数学与系统科学研究院；2.中国科学院科技战略咨询研究院；3.国家电网有限公司国网能源研究院有限公司)

1 研究背景

近年来，信息科学和人工智能推动了经济和管理领域的研究，大量的数据积累和计算技术的发展为数智化创新与管理奠定了基础，也提出了一系列的挑战。其中，利用新闻数据对经济和金融市场进行分析和预测，成为一个重要的研究方向[1,2]。我国经济领域越来越多的研究也开始应用互联网数据，通过构建舆情指数引入更广泛的市场预期，来进行价格指数水平变化的监测[3,4]。这些研究发现，互联网新闻所代表的公众舆论可能会影响投资者和消费者的期望，从而影响生产、投资和消费等经济行为，并进一步影响市场[5,6]。建立基于互联网新闻的经济舆情指数有助于发现市场变化的早期信号，以更好地预测市场未来的发展趋势。

本研究注意到不同领域的新闻舆情之间存在着复杂的相互关联。一方面，不同领域的新闻事件可能受到共同因素的影响。例如，蔬菜价格和水果价格会共同受到天气因素影响，所有的食品价格都会受到政策、突发事件及防控形势所引发的生产成本和物流成本的影响。另一方面，舆情可能会在相关的主题之间传播。比如，关于粮食价格的舆情变化可能和关于畜肉或鸡蛋价格的舆情变化之间有着相关关系，猪肉价格波动和水产品价格波动也存在关联关系[7]。这种复杂的、动态的时间和空间关联特征形成了难以用静态网络结构表征的舆情关联网络。由于新闻舆情数据在日度等更高频度或具体行业产品和领域方面往往并不连续，对不连续的新闻舆情进行数据补齐时，除了数据本身的时序特征，也应考虑到这些关联特征，才能更好地刻画舆情所反映的市场参与者预期。

图神经网络(GNN)是一种学习图结构数据的深度学习方法，具有强鲁棒性、容错性、自学习处理不确定系统等特点。GNN用于舆情数据补齐，能够充分地利用不同时间的网络中其他各节点的观测值的特征信息[8,9]。本研究以多主题舆情数据补齐为目标，构造具备学习动态图结构能力的图神经网络框架(AGNN)，探索多元时间序列的隐性图结构，在GNN学习和消息传递的基础上，实现快速有效的舆情数据补齐。

本研究的贡献主要体现在：①使用图表示法来描述某一类相互关联的经济指数所构成的系统，并且构造以分项主题为节点的有向动态图，其中分项时间序列数据为节点特征；②设计具备图学习层的AGNN网络，来学习动态图的结构变化并预测标签，通过图卷积模块捕获节点与节点邻居的空间依赖关系，通过时间卷积模块在时间维度上获取信息，二者交替进行，从而实现数据补全；③在AGNN网络图表示下，不连续的具体领域新闻舆情数据得以根据相关领域舆情变动情况补齐，相比单一时间序列补齐和K近邻等补齐方法，更能够同时纳入时间和空间的关联，解决了特定主题新闻不连续无法使用相应舆情数据进行预测的问题，促进了计算机科学、经济学和管理学领域的交叉创新。

2 文献综述

2.1 经济领域新闻数据的应用

量化新闻文本中反映出的情感倾向和舆论观点，以及汇总舆情来反映经济趋势是研究者普遍关注的方向。现今新闻数据的处理主要分为3种方法：统计方法、词典方法和机器学习方法。在统计方法的研究中，常利用主观指定的关键词的数量等文本特征来反映其情感倾向。经济政策不确定性指标(EPU)经常用于市场动态分析当中，EPU指数于2016年由斯坦福大学与芝加哥大学3位学者编制[10]，选择相关领域的报纸，统计了与经济政策相关的新闻中“不确定”这一关键词的频率，构建了反映经济政策不确定性的指标。研究表明，EPU指数与实际宏观经济变量有显著反向关系，甚至对权益市场的大幅波动也有解释作用[11]。使用机器学习方法的研究中，YADAV等[12]使用有监督的情感分析方法来处理实时新闻数据，以检验期货市场中投资者购买行为的可预测性；HAUSLER等[13]基于支持向量机处理新闻数据，分别构建了股市和房地产市场的情感指数。构建情感词典的方法在情感分析中占据主要地位，用词典来区分语义情感具有结构清晰、使用便捷和理论完整的优点。

2.2 互联网数据在价格指数领域的预测

近年来随着互联网的迅速发展，互联网数据的可获得性和可用性大大提高，已有大量研究通过用户搜索行为和评论来构建各类经济场景下的经济舆情指数。

经济指标的不稳定会直接反映国家经济社会的诸多问题，因此国内外的专家学者对于经济指标的预测十分重视。APARICIO等[14]提出了基于网购价格的CPI预测方法，通过爬取网购商品价格的数据来计算网购商品CPI，以作为外生变量对实际CPI进行预测；刘张宇[15]通过对情感分析技术、钢铁行业上下游产业链以及钢铁价格指数的系统性研究，搭建了钢铁价格指数趋势预测框架；POWELL等[16]研究集中在产品类别的平均价格，实现了自动化地预测每日消费者价格指数。同时，随着各大搜索引擎的搜索指数产品的陆续出现，搜索指数成为研究经济舆情的有力工具。张瑞等[17]基于网络搜索数据对商品零售价格进行预测；雷怀英等[18]通过对物价关键词的搜索数据进行整合，进而探究互联网数据与通货膨胀的相关性。现有的互联网数据应用于经济领域的研究结构有许多相似之处，大多基于搜索引擎数据使用主题词和趋势词建模，但基于趋势情感映射的舆情词典可综合评估不同类别词汇对语义的影响，其中包含了情感词、主题词、否定词以及程度副词等，相比原有方法，能更有效地提高量化信息的准确性[19]。

2.3 多元时间序列缺失值填补

目前已有大量关于时间序列中缺失值的填补的研究工作。传统的统计推断方法，如基于多项式曲线拟合、中值计算、均值计算等插值方法，未能利用到时间序列的信息特征和变量之间的关联关系。而一些基于机器学习的计算方法，如期望最大化算法(EM)、K-最近邻(KNN)、矩阵分解或状态空间模型，无法建模时间序列的时间依赖性。最近，一些深度学习方法在多元时间序列缺失值填补工作中取得了成功。其中应用最广泛的是基于深度循环网络(RNN)的自回归方法[20～22]。CHE等[20]提出了GRU-D的深度神经网络，通过门控循环单元(GRU)的隐藏状态来表示数据的缺失模式，并整合进模型，捕获时间序列的长时间依赖。另一种成功研究策略是利用对抗神经网络学习真实数据的完整生成序列，进而对时间序列补齐[23～25]。GUO等[25]以GRUI(一种经过修饰的GRU单元)来建模不完全时间序列，通过对抗生成模型学习时间关系、类内相似性和数据集的分布。得益于图神经网络高效的非线性时空间依赖关系捕获能力，以及可扩展性和灵活性，也有研究者将输入的多元时间序列建模为图序列，以边表示不同变量之间的关系。WU等[26]提出了一种为多元时间序列数据设计的通用图神经网络框架MTGNN，无需预先指定变量之间的关系，通过图学习模块学习多元变量之间潜在的依赖。但是现有的GNN补齐方法依赖于预定义的图结构来执行时间序列预测，除此之外，多数GNN方法只关注消息传递(GNN学习)，而忽略了图结构不是最优的并且应该在训练期间更新的事实。所以，未知图结构或已知图结构但该结构不是最佳的，对于预测来说都是需要解决的问题。

3 研究方法

3.1 研究框架

本研究从互联网新闻数据来提取特定行业变动趋势相关观点文本，首先使用基于趋势情感映射和考虑句法结构的舆情词典，对于同主题下的新闻数据进行细分，再运用该词典量化各分项的新闻文本，从而构建各个细项的日度舆情值。针对新闻数据的缺失问题，提出一种图神经网络刻画舆情指数之间的关联，以实现对于缺失指数数据节点的数据补齐。本研究将领域的分项视为节点，而分项的舆情值视为节点的特征序列，利用设计的图神经网络模型对存在的隐性图结构进行学习，发现节点之间隐藏的关联性，捕获节点间的时空依赖性，进而预测缺失值来实现缺失补齐的目的。

本研究基于互联网新闻数据来构建相关领域的舆情词典[19]，使用TextRank和TF-IDF算法选择趋势词为种子词。在这些种子词及其同义词扩展的基础上，通过集成学习Word2Vec和情感取向互信息(So-PMI)的相关性计算结果，判断情感词在舆情词典中的归属，并用标签传播算法将情感词的相关值附加到舆情字典中。同时，在舆情词典中加入程度词典和否定词典来刻画语义的强烈等级，并在句子等级进行主题匹配以提高量化文本的准确性。由于本研究构建的舆情词典具有量化新闻文本的能力，故具有文本分类的功能。以物价的子领域划分为细项舆情主题，通过所构建的舆情词典生成相应细项的日度舆情特征序列，并利用设计的AGNN图神经网络模型对存在的隐性图结构进行学习，构成关于各领域价格指数的动态舆情指数网络，捕获各细项的新闻信息来实现缺失部分的预测，进而完善舆情指数。而设计的图神经网络模型，主要由一个图学习层、n个图卷积模块以及n个扩张过滤器组成。最后，将补齐后的细项舆情指数与对应的具体统计指标进行比较分析，并构建预测模型，对所提出方法的实证效果进行检验。本研究框架见图1。

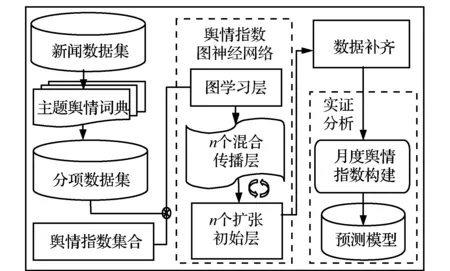
图1 研究框架

3.2 时间序列的自学习型图神经网络

使用动态图表示法来描述本研究问题后，构建AGNN自学习图神经网络模型以捕获动态网络中的信息，并且根据时序数据进行学习和优化图结构，过程中不仅考虑自身特征，还充分利用了其他观测值的特征信息，进一步完善预测效果。

模型的具体框架如下(见图2)：对于特定的领域进行主题细分，将各细分项视为节点，其时间序列数据设定为节点的特征，第i个分项的第j个特征表示为Fji。而图学习层可以自适应地学习隐形图的邻接矩阵A∈Rn×n，以捕获各个细项的时间序列数据之间的隐藏关系，邻接矩阵中的元素aij∈{0,1}，设Y∈Rn是标签集，P∈{0 or 1}n是分区，其中只有当aij=1时，Pi=1，在训练测试中观察到Yi。例如对于分项Ti,若aki=1，则表示分项Tk与分项Ti之间有有向边，方向是Tk指向Ti，同时Pk=1，即在预测分项Ti的缺失特征值时，训练过程中观察到Yk，即分项Tk的标签。对于每个分项，根据预测的标签结果选择合适的其他分项作为邻居，而每一个分项视为节点，然后通过图卷积模块(GCM)融合节点的信息和节点邻居的信息来处理空间依赖性。时间层面信息提取模块(TCM)，则是利用一维卷积滤波器来捕获时间序列数据的顺序模式，作用是捕获时间层面的节点信息。时间卷积模块通过在时间轴和节点轴上来过滤输入(用虚线框表示)，图卷积模块在每一步过滤输入(用实线框表示)，二者交替推进。通过上述模型，即可补齐节点Ti在t+1时刻的缺失值，时间窗口继续滑动至新的特征矩阵(包含补齐的特征值和未被观察的节点特征)，再次利用自学习层，获得新的邻接矩阵A。

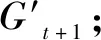
3.2.1图学习层

图学习层自适应地学习图的邻接矩阵，以捕获各个细项的时间序列数据之间的隐藏关系，而在多元时间序列预测中，希望节点的前期条件变化导致后期变化，故所学的关系应该是单向的。出于该目的，图学习层的设计有利于这种单向关系的提取，其核心公式如下：

N1=tanh(αE1θ1)；

(1)

N2=tanh(αE2θ2)；

(2)

(3)

idx=argtopk(A[i:])；

(4)

A[i,idx]=0(i=1,2,…,M),

(5)

式中，E1、E2表示为随机初始化的节点嵌入，并且在训练过程中是可以学习的；θi是模型参数；α是控制激活函数饱和率的超参数；argtopk是返回top-k的索引向量的最大值。由式(3)实现的图邻接矩阵具有不对称性质，其中减法项和RELU激活函数正则化邻接矩阵，从而体现单向性，而一般的距离度量通常是对称或者双向的。式(4)和式(5)是制作邻接矩阵的策略稀疏同时降低接下来图卷积的计算成本。对于每个节点，选择它的前k个最近的节点作为其邻居。在保留连接节点的权重的同时，将非连接节点的权重设置为零。

当图学习层学习到隐藏图结构的邻接矩阵A，矩阵A导入图卷积模块，图卷积模块实质是由两个混合跳传播层组成，当图学习层学习到邻接矩阵，混合跳传播层可以在空间层面处理相关节点的信息。

3.2.2混合跳传播层

在给定图邻接矩阵的情况下，混合跳传播层来处理空间相关节点上的信息流，其核心步骤主要为信息传播过程和信息选择过程。核心步骤的数学形式如下：

①信息传播过程：

(6)

式中，β是一个超参数，它控制保留的比率根节点的原始状态。

②信息选择过程：

(7)

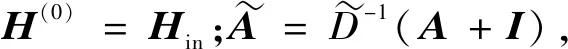
本研究保留了一部分节点的原始状态传播过程，以便传播的节点状态既可以保留自身信息，又能探索邻居节点的深层信息。如果只应用信息传播过程，将会丢失一些节点信息。因为在不存在空间依赖的情况下，聚合邻里信息只会增加无用的噪音到每个节点，引入信息选择步骤是为了过滤掉可能出现的噪音，保留下每一跳产生的重要信息。根据信息选择原理，参数矩阵W(k)功能作为一个特征选择器，并且当给定一个图结构，该图结构不包含依赖关系时，可以通过调整W(k)为0来保留原始节点的自身信息。混合传播层的传播过程见图3。

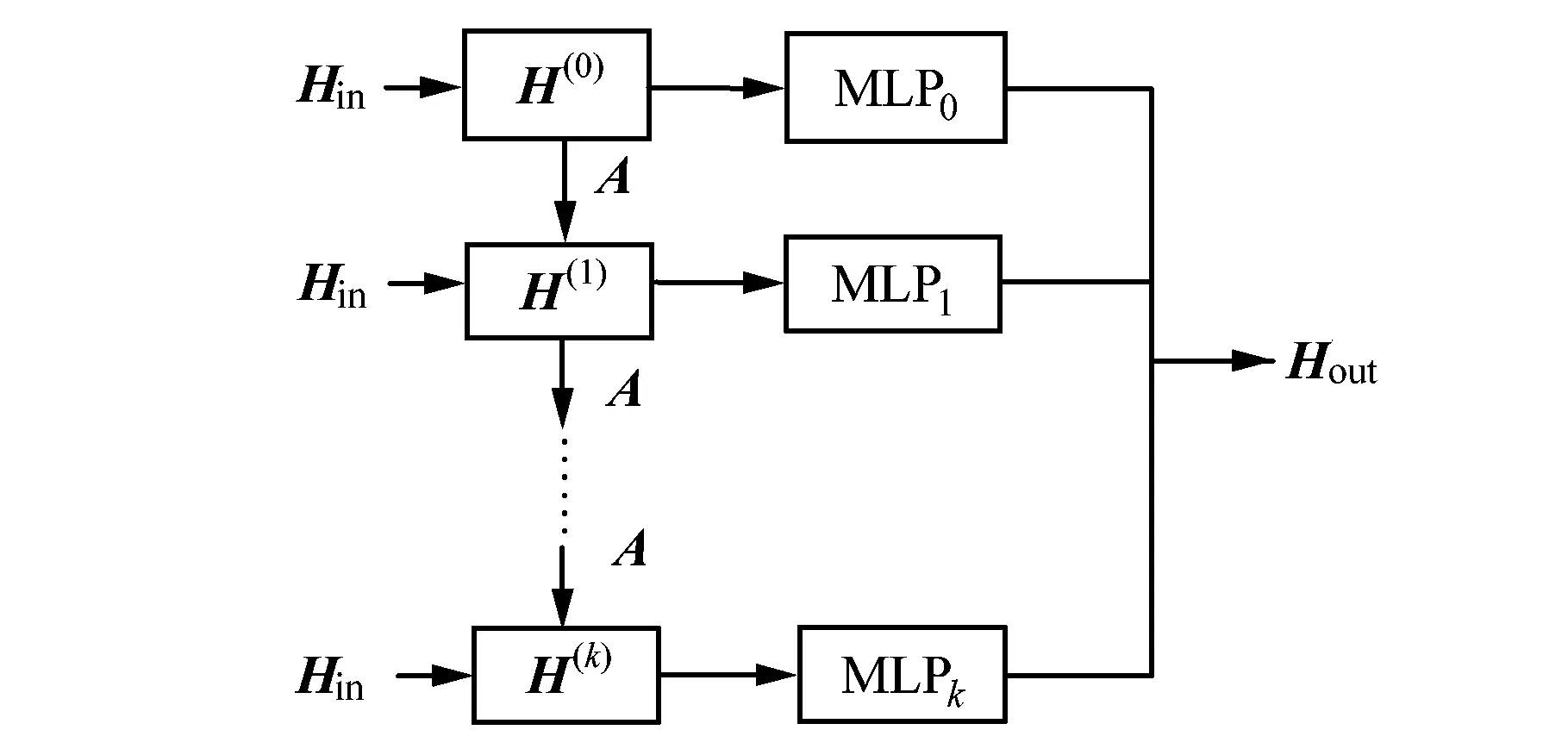
图3 混合传播层的传播过程

3.2.3扩张初始层

时间层面信息提取模块主要由两个扩张的初始层组成。一个扩张的初始层之后是一个切线双曲线激活函数作为过滤器，另一层之后是一个sigmoid激活函数，其作为一个门，来控制过滤器传递给下一个模块的信息。由于时间信号往往具有一些固有的时间周期，而量化的舆情值是日度数据，符合这些时间周期的范围，1×7尺寸的滤波器组成的时间初始层可以覆盖上述周期。同时，卷积网络的感受野大小、网络深度及过滤器内核尺寸呈线性关系增加，比如一个卷积网络具有n个一维卷积层，并且每个卷积层的内核大小为c，那么这个卷积网络的感受野大小为

感受野=n(c-1)+1。

(8)

扩张初始层可以减少模型的复杂度，因为当处理很长的时间序列，它需要一个非常深的网络即非常大的过滤器，这就意味着复杂度过高导致模型运算困难。解决该问题的具体方法为，设置膨胀因子q(q>1)，对每q步的采样输入应用标准卷积，让每一层的膨胀因子以q的指数形式增加，假设初始膨胀因子为1，内核为c的n个一维卷积层组成的卷积网络，其感受野大小为

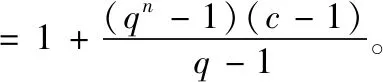
(9)

3.2.4输出层

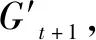
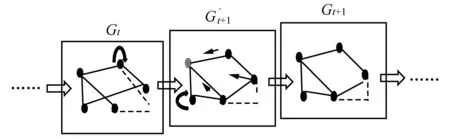
图4 节点信息捕获过程

3.3 价格舆情指数网络

3.3.1价格舆情特征提取

本研究采用基于词典的方法进行文本量化[19]，词典中的每个单词都必须对应地有一个极性得分，称为该词的观点值，观点值的大小用来衡量对应词在特定领域中的观点强度，观点值的正负反映对应词的观点方向(繁荣或衰落)。本部分的目的是，建立与所研究领域主题的新闻特别相关的基于趋势情感映射的舆情词典，其主要由种子词典、程度词典、否定词典和情感词典组成。主题舆情词典的构造框架见图5。

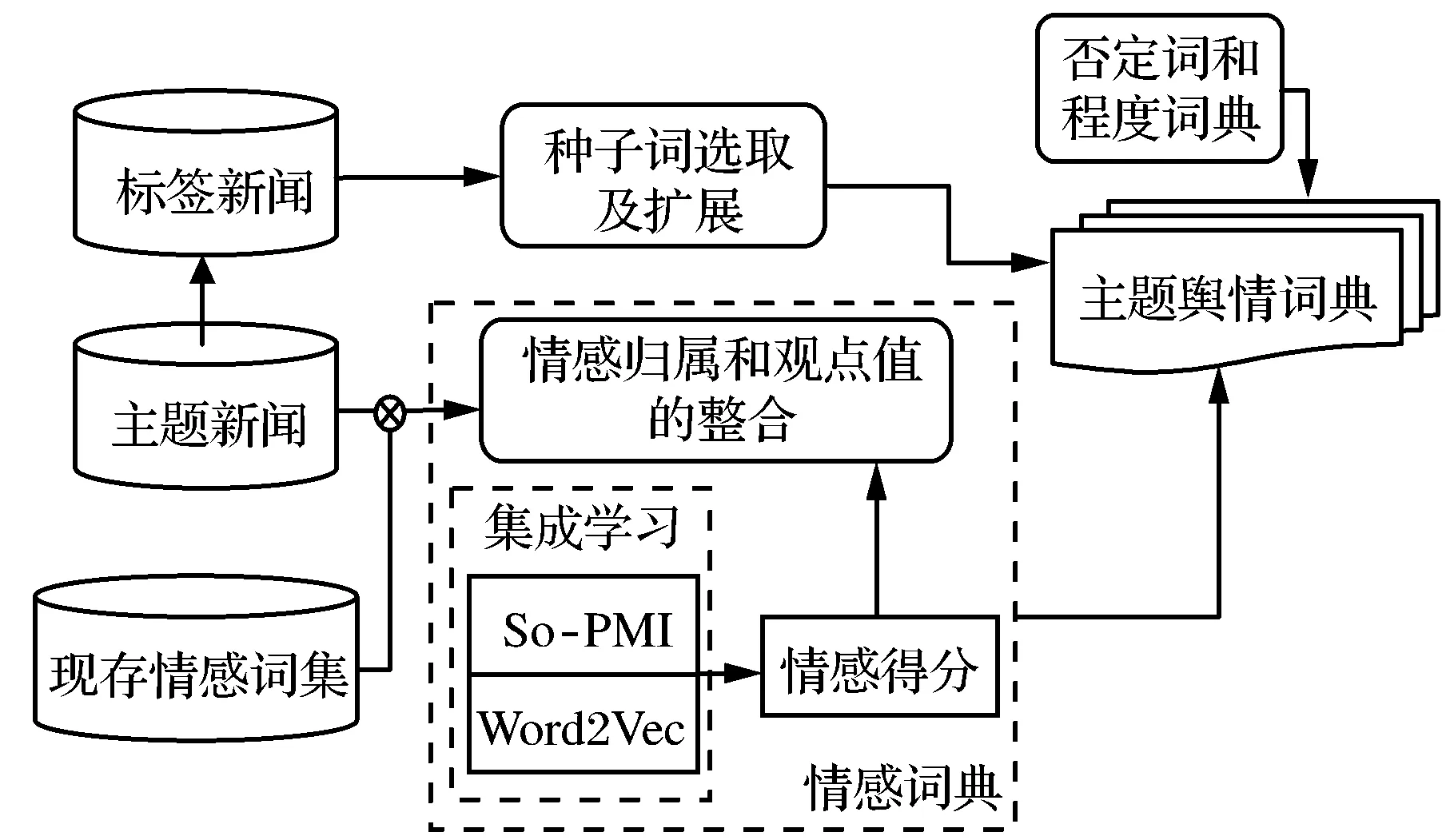
图5 舆情词典的构建

选择的种子词及其扩展为反映经济领域发展趋势的词(如“上升”“下降”等)。这样的词作为词典的“种子”，更能充分提取经济市场的动态信息。使用词频、词频-逆文本频率和TextRank算法选择种子词及其扩展。根据极性，在字典中将种子词i的观点值记为Vd,i。将在同义词林中得到的词与对应种子词组的平均相关性记为ci，则将词典中同义词i的观点值记为Ve,i。使用神经网络词向量训练Word2Vec方法和So-PMI方法对情感词进行处理，通过集成学习两种算法的极性判别结果，来获取情感词在舆情词典中的极性和相似度。情感词i的极性归属可以由相关值Tc,i或Tp,i来判断，而标签数据的敏感性分析决定判别极性的阈值ρ，本研究使用不同的阈值对情感词进行极性划分，获得Word2Vec和PMI两种算法的最佳阈值分别为ρW2V和ρPMI，从而实现情感词的极性划分。完成极性划分后，情感词的相关值Cor_I与趋势种子词及其扩展的观点值并不相关，故需要计算映射系数，将相关值Cor_I映射到趋势种子词及其扩展的观点值的值域当中。

本研究基于标签传播算法进行映射系数的计算。具体为将词典中的词定义为图模型的节点，趋势种子词及其扩展的矩阵记为FL，第i行表示第i个趋势种子词的观点值；情感词的矩阵记为FU，其每行的初始值都为0，将它们合并得到矩阵F(L+U)×1=[FL;FU]。对于图模型的边，将之前计算的Word2Vec和So-PMI算法的相关值的集成值作为图模型的边权wij。该图模型为有向图，情感词与种子词及其扩展分别对应相连，但同属性的词之间无边(边权wij=0)。由图模型的边权可以计算点i到点j的转移概率Pij，得到一个(L+U)×(L+U)维的转移概率矩阵P。进行LP算法更新，结束后FU中的值即为情感词i一一对应的映射系数θi。

经过上述步骤，可以得到情感词i的极性分组Polari、极性相关值Cor_Ii以及映射系数θi。则舆情词典中情感词i的观点值Vs,i为

(10)

式中，Up和Down分别表示上涨集合和下降集合。

3.3.2舆情指数网络

本研究使用构建的舆情词典对收集的文本按照主题进行分类，分别将食品领域和有色金属领域分为若干个细项，通过量化各细项主题下的新闻文本，构建相应的日度物价舆情值。各细项组成图的节点集，细项的日度值视为其特征序列，形成一个图结构数据。利用本研究设计的图神经网络模型对动态图结构进行学习，AGNN继续抓取节点之间的关联关系，捕获时空依赖性；然后利用已有的信息去预测缺失部分，实现各细项的舆情指数的补齐，至此构建了一个特定领域主题下的舆情指数动态网络。

量化某篇新闻文本k的表达式为

(11)

式中，Vword in k表示新闻文本k中词条的观点值，搜索当前词条前后两个词的范围，若出现程度词i，则将当前词条的观点值变换Ve,i倍；搜索当前词条前后3个词的范围，若出现奇数个否定词，则否定系数Neg=-1，否则Neg=1。

基于量化后的新闻，将同日的新闻舆情量化值求和平均。则日度舆情指数定义为

POId=Average(NVd,k)，

(12)

式中，NVd,k表示第d天的新闻值文本量化集合；Average表示求和平均。则月度舆情指数为

POIt=Average(POIt,d)，

(13)

式中，POIt,d表示第t月的日度舆情指数集合。新闻量化的初始舆情值和AGNN补齐后的日度舆情值按日期前后合并成新的日度舆情指数，可定义为

(14)

式中，POIAGNN表示通过AGNN模型补齐的舆情缺失部分。则月度舆情指数为

(15)

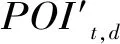
4 实证分析

4.1 食品领域价格指数预测

4.1.1数据描述

本研究采用一个经过检验的相对完整新闻数据集，筛选了来自2009年10月～2014年2月的搜狐新闻公开数据集中，正文包含“食品”“物价”“价格”“CPI”等相关字段，同时仅保留描述国内食品物价情况的新闻，最终共选出2009～2014年全国食品物价新闻219 231条。由于本研究使用的新闻数据时间在2016年前，而在2016年1月之后，国家统计局对食品项构成进行了调整，故考虑旧食品项构成并根据《价格指数生活必需品编制目录》中的食品分项关键词条筛选了9个细项数据集，分别为粮食、畜肉、食用油、水产品、蔬菜、水果、蛋类、调味品和其他食品。但是存在在某些监测日内并未有相关新闻报道的情况，所以收集的新闻数据存在着缺失问题，例如食品主题的缺失天数共计122天。

4.1.2食品价格舆情指数网络构建

物价的变化能够很好地反映通货膨胀等经济现象的趋势情况，在现有的经济指标中，居民消费价格指数(CPI)可解释一定时间内通货膨胀的变动情况，而其中食品项为最重要的组成部分，故本研究使用CPI食品项当月同比数据作为目标变量进行预测分析。使用舆情网络框架对中国食品物价新闻数据集进行量化，针对食品领域的新闻数据，网络框架是由Tensorflow中优化器AdamOptimizer使用梯度裁剪进行训练，选择的学习率为0.001，L2正则化惩罚为0.000 1。在每个图卷积模块之后应用分层形式，混合跃点传播层的深度设置为2，保留率设置为0.04。图学习层激活函数的饱和率设置为3，节点嵌入的维数不超过40。对于本研究量化的舆情值，使用6个图卷积模块和6个时间卷积模块，膨胀指数因子为2。图形卷积模块和时间卷积模块都有16个输出通道，跳过连接层都有32个输出通道，设置了9个节点，每个节点的邻域数设为不超过9，而批次大小设置为5。然后使用本研究所描述的舆情指数构建方式，构建各领域下的日度舆情值；而对于缺失的部分，利用构建的AGNN模型对9个细项进行信息捕获，将其看成9个节点，各自的日度舆情值视为节点的特征序列，图神经网络对存在的隐性图结构进行学习，预测缺失部分。得到完整的日度舆情值后，使用文中的月度舆情指数构建方法，形成各细项的月度舆情指数。根据2016年之前的食品项各构成占比：粮食(10.5%)、食用油(3.9%)、肉禽及其制品(25%)、蛋(3.4%)、水产品(6.6%)、蔬菜(12.1%)、水果(12.1%)、调味品(2.9%)和其他食品(23.5%)，最终合成了食品物价月度舆情指数POIfood。这里使用了常用的补齐方式(选择删除、均值填充和最近邻点填充)对缺失的日度舆情值进行填充，并且按照各构成占比，合成不同的食品物价月度舆情指数；同时用构建的舆情词典对食品项所有新闻进行直接量化，然后合成食品物价总舆情指数POIfood_all(见图6)。

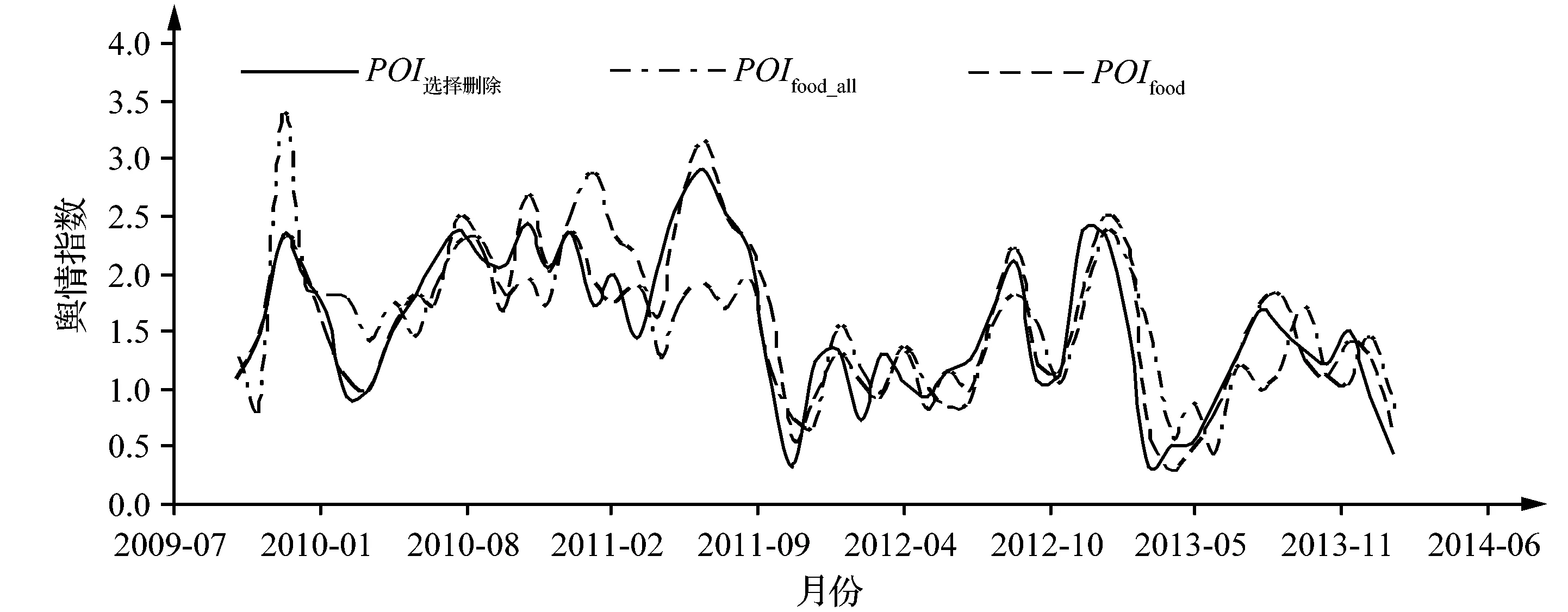
图6 不同补齐方式的舆情指数

食品项CPI和POI的Pearson相关系数见表1。由表1可知，不同方式合成的舆情指数与食品项CPI值之间具有较强的相关性，并且基于舆情网络框架构建的舆情指数和CPI值的相关系数提升至0.654，表明本研究方法可以更有效地提取信息。各细项CPI和POI的Pearson相关系数见表2。由表2可知，细项的舆情指数与CPI值之间都具有较强的相关性，例如肉禽及其制品项中两项指标的相关系数为0.845，粮食项中两项指标相关系数为0.665。进一步说明了本研究方法提取舆情信息的有效性，相比其他方法捕获了更多的信息。

表1 食品项CPI和POI的Pearson相关系数(N=324)(1)利用本研究提出的方法，量化食品价格新闻文本，得到2009年10月～2014年2月的月度舆情指数，共计54条，表1涉及6个变量，观测值总计324。表2～表4同法得到相应的观测值。

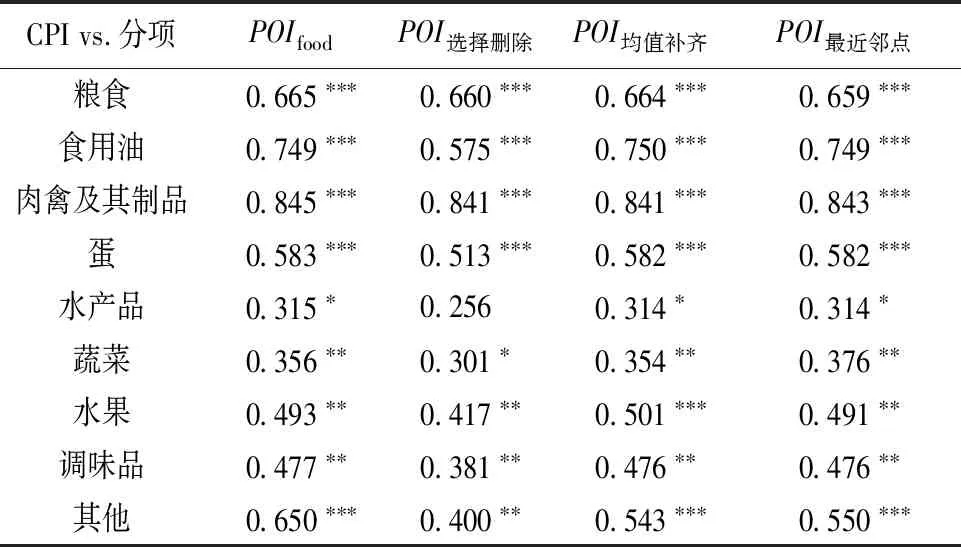
表2 各细项CPI和POI的Pearson相关系数(N=2 430)

4.1.3基于舆情物价修正的食品价格指数预测

为了探究所构建的舆情指数与食品物价之间是否存在长期稳定的均衡关系，对全国食品物价进行基于回归残差的协整检验，检验结果见表3。

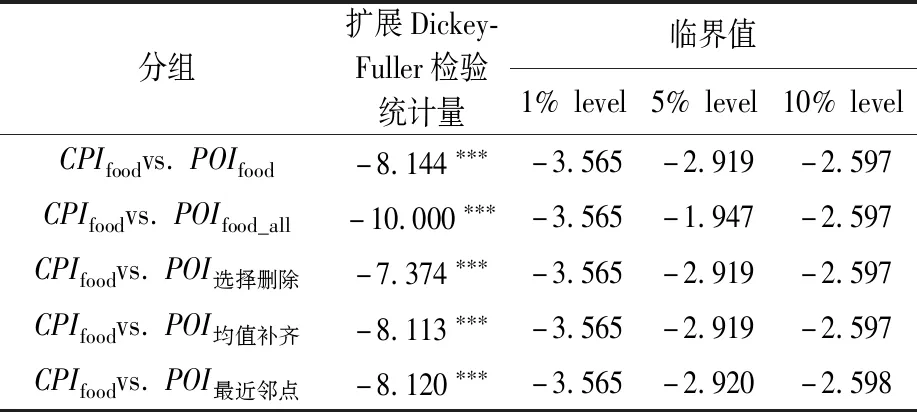
表3 食品物价和舆情指数协整检验(N=324)

协整检验的结果说明，每组的两个变量回归得到的残差序列都是平稳的，即食品物价舆情指数POI与食品项CPI存在长期稳定的均衡关系。长期均衡关系的存在也为利用舆情指数对食品物价进行预测分析奠定了理论基础。

为了进一步验证所构建食品物价舆情指数网络模型的有效性，本研究用基于食品物价舆情指数网络补齐的食品分项舆情指数集合，对消费者价格指数食品项(CPIfood)同比数据进行预测。由于食品项CPI指数具有较强的季节性和趋势性，首先通过X13季节调整加法模型剔除季节因素后，保留季节调整后值(SA项)。而ARIMA模型在经济预测过程中既考虑了经济现象在时间序列上的依存性，又考虑了随机波动的干扰性，对于经济运行短期趋势的预测准确率较高[27]，模型只考虑内生性而不需要外生变量。由于本研究的核心是探索舆情指数是否对食品价格指数变化存在外生影响，所以使用食品项CPI的SA项数据构造自回归滑动平均预测模型(ARIMA)，以去除数据本身内生性带来的效益，将预测的SA项值还原为预测的食品项CPI，与实际的食品项CPI比较分析。本研究使用2009年10月～2013年6月的食品物价舆情指数POIfood、食品物价总舆情指数POIfood_all、选择删除补齐的食品物价舆情指数POI选择删除、均值补齐的食品物价舆情指数POI均值补齐、最近邻点法补齐的食品物价舆情指数POI最近邻点分别与ARIMA模型得到的残差构造最小二乘法回归模型，进行误差修正。

(1)ARIMA模型的确定

对食品项CPI的SA项进行ADF单位根检验，结果显示数据是一阶差分平稳，可以设定ARIMA模型参数d=1；然后根据AIC准则和BIC准则，确立最合适的ARIMA模型参数p=1，q=1；最终选择ARIMA(1,1,1)作为预测模型。模型表达式为

ΔYt=c+β1ΔYt-1+γ1μt-1+μt，

(16)

式中，c为常数项；β1为自回归系数；γ1为移动回归系数；{μt}为白噪声序列。

由ARIMA模型直接预测的Yt为食品项CPI的SA项预测值，然后通过季节调整的加法模型还原为CPI预测值：

CPIt=Yt+季节调整因子t；

(17)

季节调整因子=CPItrue-(TC+I)，

(18)

式中，TC表示季节调整后的趋势循环项；I为不规则要素。

基于该模型的食品项CPI预测结果见图7。由图7可知，预测结果与实际值之间的差距呈现一定的规律性，在大部分时间ARMA模型的拟合值都略微滞后于CPI的实际值。这与现有的CPI预测实证研究中的结果一致[27,28]。

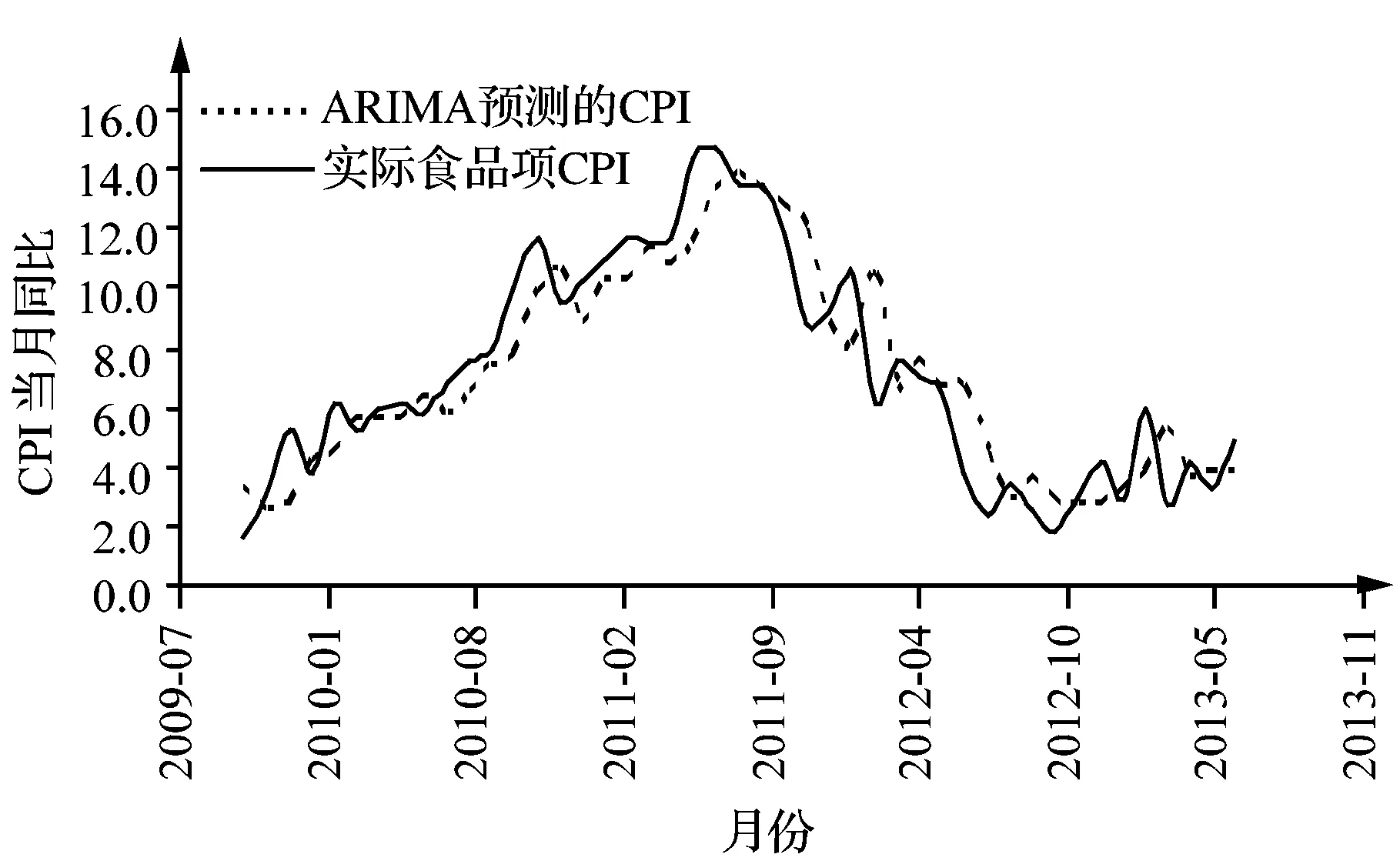
图7 ARIMA预测食品项CPI和实际食品项CPI

(2)食品项CPI的误差修正

ARIMA模型中误差的产生是由于其只考虑了数据本身所在的时间序列特征，并没有考虑外生变量对物价的影响。由于物价相关舆情从一定程度上可以体现很多方面对于物价的外来影响，而根据协整检验的结果可知，本研究构建的舆情指数和食品项CPI是存在长期稳定的均衡关系。因此，这里用本研究构建的食品分项舆情指数来修正食品项CPI预测值的误差，选择OLS回归模型，并使用最优子集回归的方法进行变量筛选。由于OLS回归模型为时间序列模型，允许变量滞后项参与回归过程，则生成各种食品物价舆情指数的1～3阶滞后。经过最优子集回归，根据AIC、BIC、Cp准则以及拟合优度R2，以ARIMA残差(σ)为因变量，分别生成5种食品物价舆情指数的误差修正模型，模型的基本形式为

模型1：

σ=α11POIfood_all+α12POIfood_all(-1)+δ1；

(19)

模型2：

σ=α21POI选择删除+α22POI选择删除(-1)+δ2；

(20)

模型3：

σ=α31POI均值补齐+α32POI均值补齐(-1)+

α33POI均值补齐(-2)+δ3；

(21)

模型4：

σ=α41POI最近邻点+α42POI最近邻点(-1)+

α43POI最近邻点(-2)+δ4；

(22)

模型5：

σ=α51POIfood+α52POIfood(-1)+

α53POIfood(-2)+δ5，

(23)

式中，αij(i=1,2,3,4,5;j=1,2,3)为回归系数；δi(i=1,2,3,4,5)为随机误差项。然后将由舆情指数修正的残差与ARIMA的预测值进行结合，再考虑季节调整因子的因素，得到最终的食品项CPI的预测值为CPIt=Yt+季节调整因子t+σt。

4.1.4预测结果分析

使用处理好的数据集对模型1～模型5和ARIMA模型分别建立预测模型，进行静态的样本内的预测(IN)，时间区间为2009年10月～2013年6月。对模型的预测结果评估依据均方误差(MSE)、误差均方根(RMSE)、平均绝对误差(MAE)、平均相对误差绝对值(MAPE)、对称平均绝对百分比误差(SMAPE)5个指标来评判。为了探究舆情指数在样本外预测的效果，对6个模型分别建立预测模型，进行动态的样本外预测，使用时间区间为2009年10月～2013年6月的样本数据对2013年6月～2014年2月进行预测，样本内外的预测效果对比见表4。

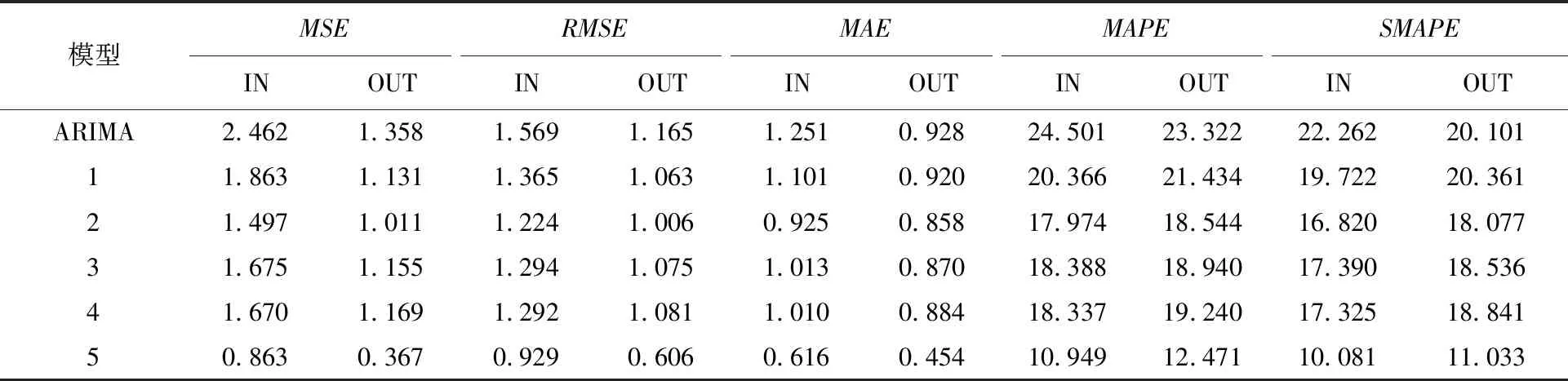
表4 预测结果对比(N=1 620)

由样本内预测结果可知，用食品物价舆情指数对ARIMA误差进行修正后的预测模型，其所有评价指标都逐渐减小，有更加良好的预测结果，并且基于AGNN舆情指数网络的误差修正预测模型各项指标均达到最小。而样本外预测结果表明，加入食品物价舆情指数对预测精度有所提高，并且分细项后再合成的舆情指数能捕获更多的信息，从而更好地预测食品项CPI。除此之外，构建舆情指数网络来实现数据补齐的方式是效果最好的，其涉及的预测模型评价指标也是6个模型中数值最小的，有良好的样本外预测效果。样本内和样本外的预测验证了所构建的全国食品物价舆情指数的有效性，通过对食品项CPI进行预测建模，能够提高食品项CPI的预测精度，为全国食品消费市场的预测研究作出贡献。

4.2 有色金属领域价格指数预测

4.2.1数据描述

为了进一步验证本研究方法的合理性和可扩展性，尝试建立有色金属行业领域基于互联网新闻的舆情指数网络，爬取了来自中国有色网2015年1月～2021年12月的新闻数据，进行数据清洗过滤，最终共保留2015～2021年全国有色金属行业新闻5 604条。

4.2.2有色金属领域舆情指数网络构建

以主要有色金属的价格及需求为主题进行分项，构建有色金属领域的舆情网络，利用本研究方法填补缺失部分，针对有色金属领域的新闻数据，混合跃点传播层的深度设置为2，保留率设置为0.05。图学习层激活函数的饱和率设置为2.5，节点嵌入的维数不超过30。对于本研究量化的舆情值，使用5个图卷积模块和5个时间卷积模块，膨胀指数因子为2。图形卷积模块和时间卷积模块都有10个输出通道，跳过连接层都有20个输出通道，设置了8个节点，每个节点的邻域数设为不超过8，而批次大小设置为4。

合成有色金属行业价格舆情指数(POIprice)和需求舆情指数(POIdemand)，与有色金属的工业生产者出厂价格指数(PPI同比)进行相关性分析，并和其他补齐方法进行比较，结果见表5。由表5可知，基于舆情网络框架构建的舆情指数和PPI值的相关系数提升至最高，表明本研究补齐方式可以更有效地提取信息。

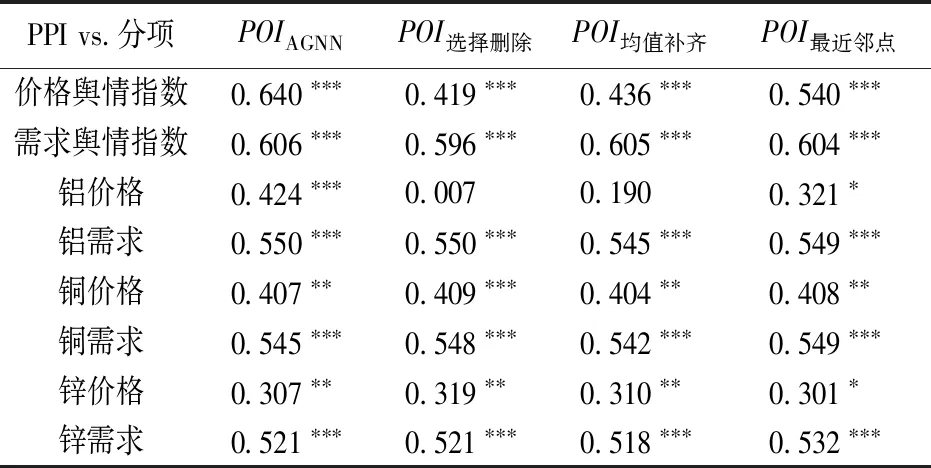
表5 有色金属舆情值与有色金属PPI的Pearson相关系数(N=3 060)(2)利用本研究提出的方法，量化有色金属行业新闻文本，得到2015年1月～2021年12月的月度舆情指数，共计84条，表5涉及40个变量，观测值总计3 360。表6同法得到相应的观测值。

4.2.3基于舆情修正的有色金属行业价格指数预测

同理，对有色金属PPI的SA项进行ADF单位根检验，结果显示数据是一阶差分平稳，可以设定ARIMA模型参数d=1，并根据AIC准则和BIC准则，确立最合适的ARIMA模型参数p=1，q=2，并且协整检验说明，有色金属舆情指数POI与有色金属行业PPI存在长期稳定的均衡关系。因此，最终选择ARIMA(1,1,2)作为基准模型，然后用本研究方法构建的主题舆情指数来修正有色金属PPI的预测残差，根据AIC、BIC、Cp准则以及拟合优度R2，以ARIMA残差(σ)为因变量，分别生成有色金属行业舆情指数的误差修正模型为

模型1(ARIMA+POI选择删除)：

σ=ω11POIprice(-1)+ω12POIprice(-2)+

ω13POIdemand(-1)+δ1；

(24)

模型2(ARIMA+POI均值补齐)：

σ=ω21POIprice(-1)+ω22POIprice(-2)+

ω23POIdemand(-1)+δ2；

(25)

模型3(ARIMA+POI最近邻点)：

σ=ω31POIprice(-1)+ω32POIprice(-2)+

ω33POIdemand(-1)+δ3；

(26)

模型4(ARIMA+POIAGNN)：

σ=ω41POIprice(-1)+ω42POIprice(-2)+

ω43POIdemand(-1)+δ4，

(27)

式中，ωij(i=1,2,3,4;j=1,2,3)为回归系数；δi(i=1,2,3,4)为随机误差项。

4.2.4预测结果分析

使用处理好的数据集对模型1～模型4和ARIMA模型分别建立预测模型进行静态的样本内的预测(IN)和动态的样本外的预测(OUT)，使用时间区间为2015年1月～2021年6月的样本数据对2021年7～12月进行预测，样本内外的预测效果对比见表6。

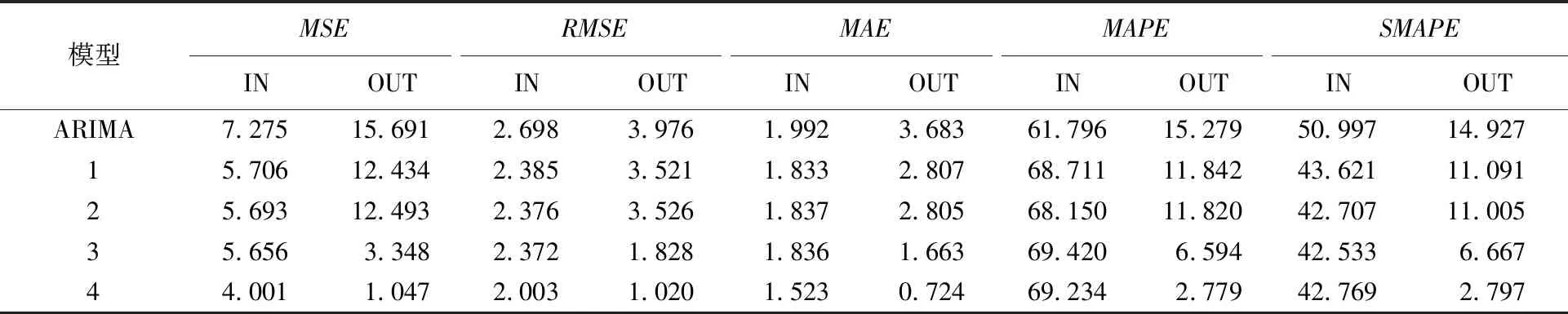
表6 有色金属预测结果对比(N=4 100)

由预测结果可知，构建舆情指数网络来实现数据补齐的方式是效果最好的，其涉及的预测模型评价指标也是诸多模型中数值最小的，有良好的样本外预测效果。样本内和样本外的预测验证了所构建的有色金属舆情指数的有效性，通过对有色金属PPI进行预测建模，能够提高预测精度，本研究所提出的方法适用于不同的价格指数领域，具有扩展性和实用性。

5 结语

本研究构建了特定领域下的舆情指数动态网络，解决了舆情指数构建中由于新闻数据稀疏性导致的连续性和一致性等问题，能更有效地提取公众舆情观点。实证检验显示，本研究所提出的方法可提高基于舆情数据进行食品价格和有色金属价格预测的精度。由于构建过程中仅采用了来自特定领域的新闻数据集和价格指标时间序列，并没有采用其他外生变量数据信息，所以本研究提供了一种不依赖于领域经济知识的建模和预测方法，是数据驱动的便于应用于其他类似领域的方法，具有较好的可扩展性。

本研究将动态图结构的神经网络用于舆情趋势推断，为更好地获取新闻数据中舆情信息提供了一种方法，并且在与其他方法的比较过程中显示出更好的性能，基于本研究舆情网络框架构建的食品物价舆情指数和有色金属舆情指数，与食品CPI和有色金属行业PPI的相关系数结果表明，本研究方法可以更有效地提取信息。另外，在食品项价格指数方面，细项的舆情指数与各自CPI值之间都具有较强的相关性；有色金属行业领域方面，细项的舆情指数与PPI之间也具有强相关性，进一步说明本研究方法的有效性。在这种图形表示下，特征插补可以自然地表示为节点级的预测任务，而标签预测作为动态图随时间变化的参考依据，构造出具备学习动态图结构能力的图神经网络框架，并且考虑了数据的特征性质和标签类型，能更好地利用数据信息。仅需要从时间序列本身提取时序特征，利用舆情信息所蕴含的外部信息作为外生变量的来源对时序预测模型进行修正，从而实现快捷有效的时序预测。根据样本内和样本外预测结果可知，在食品物价领域中，该预测模型的预测误差均为6个预测模型中最低值；而在有色金属行业领域中，基于舆情指数网络方法的预测效果显示最佳。

本研究仅以单变量时间序列作为CPI预测和PPI预测的基准模型进行实证设计，没有考虑其他外生变量；在后续的研究中，将设计方法来验证舆情变量是否能够完全涵盖其他外生因素对于目标时间序列的影响。虽然本研究方法具有一般性，但在其他领域应用中可能会需要进行模型算法的调整和改进，同时需要进一步考虑经济变量理论上的关联作为网络结构生成的约束。