跨声速流场扰动模态与湍流度精细测量
2023-03-28朱博廖达雄陈振华陈吉明
朱博,廖达雄,陈振华,陈吉明
1.中国空气动力研究与发展中心 设备设计与测试技术研究所,绵阳 621000
2.中国空气动力研究与发展中心 空气动力学国家重点实验室,绵阳 621000
人们很早就发现飞机螺旋桨叶尖附近存在跨声速流动,为方便研究跨声速流动引起的飞机操纵面颤振、失效等严重问题,需要研制地面模拟试验的风洞设备,建立与飞行器来流近似的跨声速流场[1-2],通过大量风洞试验复现、研究和解决关键问题。风洞流场质量关系到试验结果的精准度,由于流场湍流度对飞行器气动力系数影响较大[3-4],对非定常试验、边界层转捩试验和洞体结构疲劳都有着非常不利的影响,因此湍流度是风洞流场质量的关键指标之一[5-6]。
近年来,高速飞行器设计日趋精细化,在增升减阻、层流翼型、高速巡航经济性和稳定性控制方面的先进性研究,对跨声速风洞流场品质和试验精准度提出了更高要求。因此,研制新型高性能跨声速风洞是当前的重要工作,精确测量跨声速流场湍流度是关键技术之一[7]。但是,如何准确测量高速可压流场湍流度,尤其是复杂的跨声速流场模态和湍流度,一直是困扰国内外学者的难题[8-9]。
目前,风洞流场湍流度测量的主要仪器是热线风速仪,其在空气动力学中的应用有百余年历史,借助于现代电子技术和计算机高速处理能力,凭借高精度、高频响和易用性的特点,逐渐成为测量低速风洞流场湍流度的标准方法,但是,在高速可压流中的应用还存在诸多问题,需要解决热丝易断,尤其是可压流数据分析问题。1947 年,美国NASA 兰利中心成功研制世界上第1 座跨声速风洞之后,美国学者较早开展了热线测量可压流场的研究,其中,Kovasznay[10]首次建立了基于连续变热线过热比的可压流场流量脉动和总温脉动测量分析方法,此后,变热线过热比测量方法成为热线测量方法的一种重要技术基础。由于早期跨声速流场的稳定性控制技术不成熟,加之马赫数Ma≈1 时的流场较复杂,对其流动机理还有待了解,因此相关试验研究主要是在马赫数Ma>2 的超声速流场进行。Morkovin[11]认为这种超声速测量方法不能直接用于亚、跨声速可压流测量,因为实际上高亚声速时流场速度灵敏度系数与密度灵敏度系数不等,所以提出分别标定灵敏度系数,再通过变热线过热比求解脉动量值。Horstman 和Rose[12]研究认为速度灵敏 度系数与密度灵敏度系数不等只是热线在低过热比时的特征,在高过热比时速度灵敏度系数与密度灵敏度系数高度近似,因此可以利用高过热比测量流场流量脉动。Stainback 等[13]认为跨声速流场远比超声速流场复杂,在一些情况下热线的速度灵敏度系数与密度灵敏度系数不等,通过扰动模态分析和方程简化可以求解流场脉动参数。近年,由于高空高速层流翼型和高性能航空发动机研制的需求,国外学者根据流场测试需求发展了针对特殊高速流场的湍流度测试技术。King等[14]根据热线在高过热比条件下速度灵敏度系数与密度灵敏度系数高度近似的特点,利用高温单过热比方法开展了最低温度116 K 的跨声速流场测试,根据湍流度测量结果优化并评估了美国NTF(National Transonic Facility)低温高雷诺数跨声速风洞的层流试验可行性。Bauinger 等[15]在涡轮机试验中采用三维热线进行了跨声速流场测量,采用傅里叶滤波方法获得湍流度分布。还有学者以激光多普勒测速法为基础开展了高速可压流场湍流度测量研究,但是由于示踪粒子跟随性和分子散射叠加背景光噪声等因素,导致测量精度难以满足跨声速流场湍流度高精度测量需求[16-18]。
国内基于热线的高速可压流场湍流度测量研究最早是在20 世纪80 年代,恽起麟和赵长安[19]采用单过热比方法完成了马赫数为0.5~1.2 的流场湍流度测量,由于单过热比方法无法分辨流场中的速度、总温和密度脉动,因此测量精度较低。此后的相关研究很少,由于技术有限,国内许多跨声速风洞缺少试验段流场湍流度数据,或者采用风洞稳定段湍流度来近似推算试验段湍流度,由此而产生的试验误差缺乏研究和修正。近年,马护生等[20]开展了马赫数为0.7 以下基于单过热比的多项式数学模型的热线校准和湍流度测量。杜钰锋等[8,21]推导了可压流恒温式热线的响应公式,优化了变热线过热比测量方法,开展了马赫数为0.7 以下的变热线过热比可压流场湍流度测量。
由以上可以看出,现有的高速流场湍流度热线测试有单过热比和变过热比方法,在理论认识上的差异和试验测试的难度导致未能形成统一方法。国外对超声速流场湍流度测量研究较多,对跨声速流场湍流度测量研究相对较少,近年主要集中于跨声速流场的精细化测量。国内早期风洞缺少跨声速流场湍流度数据,近年对高速可压流场的精细测量研究主要在马赫数为0.7 以下,而马赫数为0.8 以上的流场湍流度精细测量研究较少,缺乏流场扰动模态分析。
本文在理论上推导了变热线过热比测量高速可压流场扰动的一般模态和3 种特殊模态特征方程,以此为基础,在新型高性能跨声速风洞上,完整测量了马赫数为0.20~1.50 的跨声速流场。通过试验测量获得了一般模态、涡模态和声模态扰动特征图,进而计算得到高精度的流场低湍流度指标,建立了一种可压流场扰动模态与低湍流度测量方法。测量结果为高性能跨声速风洞流场评估、优化和飞行器风洞试验提供了依据。
1 试验设备与测量仪器
1.1 试验设备
试验在中国空气动力研究与发展中心新建的0.6 m 变密度连续式跨声速风洞上进行,风洞及测点位置示意图见图1。该风洞设计采取了一系列降低风洞气流脉动、改善风洞流场品质、提高风洞试验效率等关键技术措施[5],试验段马赫数为0.20~1.50,稳定段总压为(0.05~2.50)×105Pa,气流总温为273~333 K,湍流度设计指标为0.05%~0.25%。风洞设置5 层阻尼网,采用压缩机动力,具有试验时间可以连续运行的优点,满足较长时间高流场品质的变热线过热比测试和低湍流试验需求,热线测点位于图1 试验段核心流A点位置。
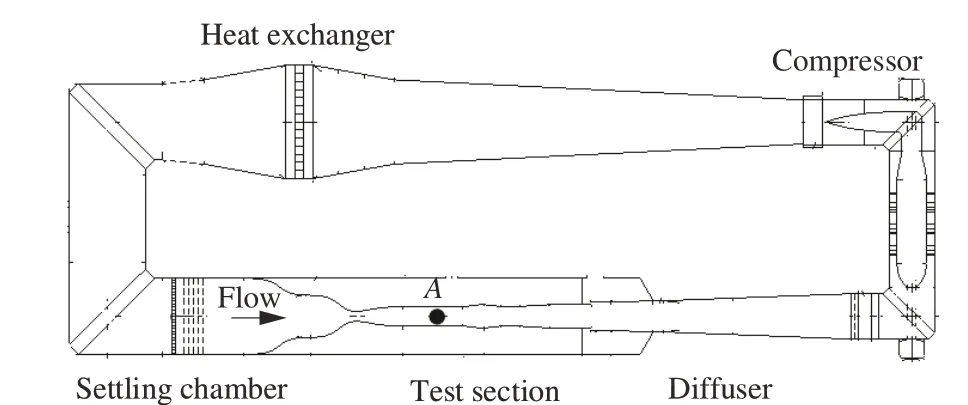
图1 0.6 m 连续式跨声速风洞及测点位置示意图Fig. 1 Schematic of 0.6 m continuous transonic wind tunnel and test point
1.2 测量仪器
测量仪器采用丹麦丹迪公司的Streamline 恒温式热线风速仪和55P11 一维探头,采集卡数据分辨率16 位。
热丝材料采用直径为5 μm 的镀铂钨丝,长度为1.25 mm,电阻温度系数为0.003 6/K。钨丝强度高但是易氧化,增加镀铂层可以降低钨丝的高温氧化效应,保证热丝在较长工作时间内的稳定性,同时重点对探头焊点进行加固,增加了探头热丝的抗断强度。
2 扰动模态与湍流度测量方法
2.1 变热线过热比测量方法
连续式风洞试验段流场覆盖亚跨超声速范围,流体具有可压缩性,存在速度、密度和温度脉动,热线输出电压与流体速度、密度、总温相关,其可表示为
式中:e为热丝输出的电压;ρ为流体密度;u为流体速度;T0为流体总温。
因此,热丝相应的灵敏度系数值不可忽略不计,采用变热线过热比方法测量获得一组方程,进而求解灵敏度系数及流场脉动量是一种有效的方法。
对式(1)采用全微分方式表示,并进行取对数、求偏导运算后得到热线对可压流体响应的关系为
考虑测量中是以热线输出电压信号的均方根偏差来计算脉动值,而且脉动参数之间存在耦合关系,因此对式(2)两边进行平方运算得
由式(3)可见,若先校准获得灵敏度系数,再以不同热丝过热比采集6 组以上数据,就可以得式(3)中的6 个脉动量值,但是这种测试方法在试验中不多见。因为方程组矩阵系数条件及其耦合关系容易导致奇异解,更为困难的是灵敏度系数校准难度很大。在风洞校准热线系数时,直接校准每一个灵敏度系数需要保持其他敏感参数不变,这对风洞运行时间和流场参数控制能力提出了极高要求。同时,增压变密度校准可使气流中的颗粒物随气体密度增加而增加,导致热丝更容易被打断,因此,直接校准的方法可行性不高。
由此,减少方程中的未知数,首先求解流量灵敏度系数及其脉动量更为可靠,考虑将热丝对流体速度和密度的灵敏度统一考虑为流量灵敏度,即
式中:m为流量。
对式(4)采用全微分方式表示,并进行取对数、求偏导、平方运算后可得
通过精确控制风洞流量,可以轻易校准式(5)的热线流量灵敏度系数Sm。方程中的总温灵敏度系数ST0仍然不易直接校准,需要从热丝的热平衡关系式推导总温灵敏度系数。
恒温式热线的热平衡关系式[22]为
式 中:A与B为热丝 的雷诺数Re校准系数;Rw为热丝的工作电阻;l为热丝长度;λ0为气体导热率;Tw为热丝的工作温度;Te为热丝在流场中的非工作温度;k为热丝变过热比响应系数;aw为热丝过热比。
式中:Re为热丝在流场中的非工作电阻。雷诺数的定义式为
式中:d为热丝的特征长度;μ为流体动力黏性系数。
将式(8)代入式(6),并对式(6)两边取自然对数再求偏导,整理后可得
即
式中:FCTA为恒温式热线的流量灵敏度系数;GCTA为恒温式热线的总温灵敏度系数;α*为热丝的电阻温度系数;R*为热丝在参考温度时的电阻值;η为可压流温度恢复系数。
本文试验采用的热丝长度为1.25 mm,在马赫数为0.20~1.50 时,热丝雷诺数Re介于5 500~18 000,热 丝 变 过 热 比 响 应 系 数k[21]为0.11~0.14,由于k远小于Re,则式(10)第2 项数值极小,FCTA主要取决于式(10)第1 项的值。对式(10)第1 项分数上下同时除以,由于系数A与B为同一量级,则的值也较小,因此,式(10)第1 项的值约等于0.25,即FCTA的值约等于0.25。进一步,根据式(11)可以计算恒温式热线的总温灵敏度系数GCTA。
2.2 一般扰动方程与流量总温脉动量计算
对式(9)两边除以GCTA,再取平方,得到热线变过热比响应的一般扰动方程为
根据式(12),作θ值与r值的拟合曲线,可得流场扰动模态,如图2 所示。由r的定义可知:当r值趋向无穷大,则热丝对总温敏感度极小(可以忽略),热丝主要对流量敏感,因此,拟合曲线的渐进线的斜率等于流量脉动值m。当r值趋向0,则热丝对流量敏感度极小(可以忽略),热丝主要对总温敏感。因此,令r=0,则拟合曲线与Y轴的交点等于总温脉动值。RmT0值是流量与总温脉动量的相关系数,计算方式为实测的流量、总温脉动量耦合值与2 个脉动量之积的比值,反映了实测值与理论值的相关性。一般情况下,流量与总温脉动量具有弱相关性,相关系数RmT0较小,此时,由于流量灵敏度系数随着过热比升高而升高,总温灵敏度系数随着过热比升高而降低,因此,拟合曲线为双曲线特征。
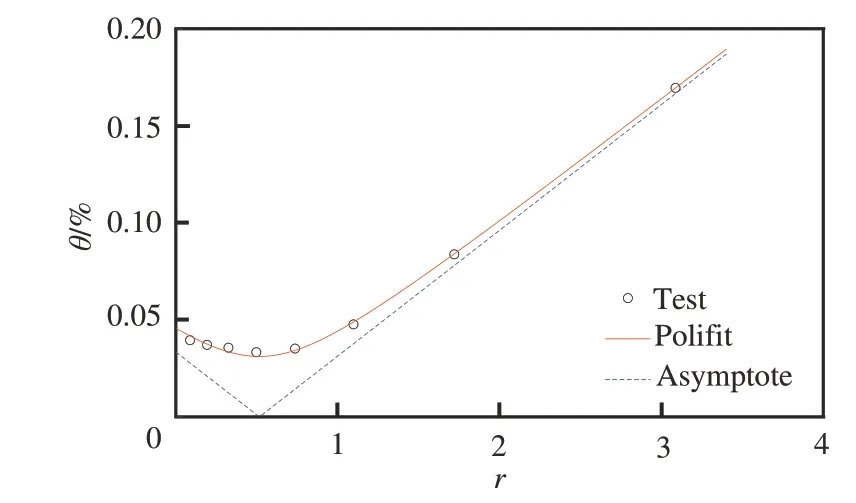
图2 马赫数为0.70 时的流场双曲线一般扰动模态Fig. 2 Hyperbola general fluctuation at Ma=0.70
若实测相关系数RmT0≥1,说明流场模态发生了改变,实测值的脉动量已经转变为或者其中一种脉动量主导的扰动,式(12)将退化为一次方程,扰动图的特征也将发生改变。当流场扰动量主要为速度脉动时,流场扰动模态为涡模态;当流场扰动量主要为温度脉动时,流场扰动模态为熵模态;当流场扰动量主要为静压脉动时,流场扰动模态为声模态[10]。
由质量流公式m=ρu,两边取自然对数求偏导处理,可得
由一维等熵关系式,得
式中:T为流体静温;γ为比热比;Ma为马赫数。
参考文献[8],将式(14)两边取自然对数求偏导处理,并与式(13)一起代入式(9),整理后可得热线变过热比响应的一次方程表达式,即
式中:α=[1+(γ-1)Ma2/2]-1;β=α(γ-1)Ma2。
式(15)是流场以一种脉动量为主导、各种脉动量之间的耦合值极小(可以忽略)时的脉动量解析表达式。2.3~2.5 节将根据式(15)对流场涡、熵、声模态的特征方程及其扰动图的特征形态进行分析。
2.3 涡模态扰动方程
式(16)表明,流场涡模态的扰动图特征为V形折线,折线的折点在X轴上r=β位置。
2.4 熵模态扰动方程
熵模态流场存在温度脉动和温度脉动引起的密度脉动,速度脉动和压力脉动为0。
由理想气体状态方程,得
式中:R为理想气体常数。对式(17)取自然对数求偏导处理,可得
式(20)表明,流场熵模态的扰动图特征为直线,当r=-α时,直线与X轴相交。
2.5 声模态扰动方程
声模态流场存在声波(静压)扰动产生的流场温度、速度和密度波动,流动遵循等熵方程,声波扰动具有方向性。
由等熵过程压力与密度的关系,得
式中:C 为常数。
对式(21)取自然对数求偏导处理,得
将式(22)代入式(18),可得
将式(22)和式(23)代入式(15),可得
由于流场中声波引起的流量不变,即
式中:ua为声波的扰动速度。对式(25)两边取自然对数再求偏导,可得
其中:c为声速。
由马赫数定义,得
将式(22)和式(27)代入式(26),整理可得
设流速u与声波ua的夹角为χ,则有
将式(29)代入式(24),可得
由式(30)可知,声学模态扰动图受流场速度和声波方向影响,可以出现直线或者V 形折线特征,拟合线与X轴相交于:
由于连续式风洞试验段沿流向的附面层厚度逐渐增大使得流场下游噪声逐渐增大,加之下游弯刀支架和引射缝噪声等影响,导致试验段下游噪声往往大于上游,声波方向为180°,可得cosχ=-1,拟合线与X轴相交于:
此时,声学模态扰动图特征为直线。
2.6 湍流度计算
湍流度与噪声是跨声速流场中的2 种主要扰动量[9],其中,流场噪声为无旋扰动,其产生的静压脉动同样可以导致速度波动,因此,对流动的扰动模态可区分涡模态(速度脉动)和声模态(静压脉动),而在计算湍流度时,应忽略静压脉动量分解项[8],把静压脉动导致的速度脉动也计算为流场湍流度,因此,从流量脉动量中主要分解出速度脉动量和密度脉动量。
由式(13)两边平方,可得
由声速的定义,得
对式(14)、式(27)、式(34)取自然对数求偏导后,与式(18)代入式(33),忽略静压脉动量分解,整理可得
将式(12)求解的流量脉动值、总温脉动值和相关系数代入式(35)、式(36),分别可得流场湍流度值和密度脉动值。
2.7 热线仪试验参数优化
Streamline 热线仪为恒温式热线,采用20 m信号线时,低过热比状态与高过热比状态的频率响应之差可达1 倍,响应频率不一致可引入测量误差。为此,在测量前采用方波测试并调理热线各过热比的通道增益,使得在不同过热比下的通道频响大于10 kHz,再通过设置低通滤波器参数,使得不同过热比下的通道频响均在10 kHz的一致水平。
由于低过热比时通道信噪比较低,可导致热线数据失真,因此不宜设置太低的热线过热比,本文设置热线最低过热比为0.1。在试验中,通过程序控制热线仪先测量热丝在当前流场的冷丝电阻,再根据冷丝电阻设置热丝过热比的桥电阻,依次设置0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8 等8 个过热比,进行数据采集。数据采样频率为20 kHz,单点采样时间为5 s,Streamline 热线仪完成8 个过热比设置和数据采集大约需要3.5 min。
3 试验结果与数据分析
3.1 流场扰动模态与流场脉动参数
图2~图4 是根据式(12)采用相同方法测量获得的试验流场3 种典型扰动模态图,其中,图2流场速度为马赫数0.70,拟合曲线的特征为双曲线;图3 流场速度为马赫数0.40,拟合曲线的特征为直线;图4 流场速度为马赫数0.80,拟合曲线的特征近似于V 型折线。
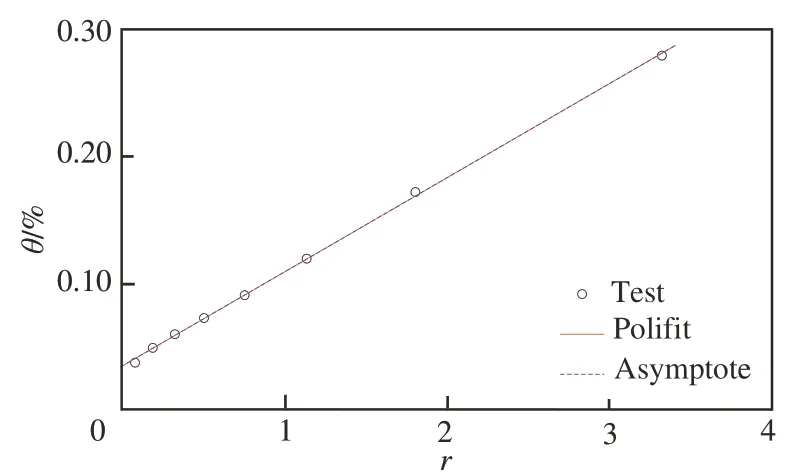
图3 马赫数0.40 流场声模态扰动Fig. 3 Acoustic mode fluctuation at Ma=0.40
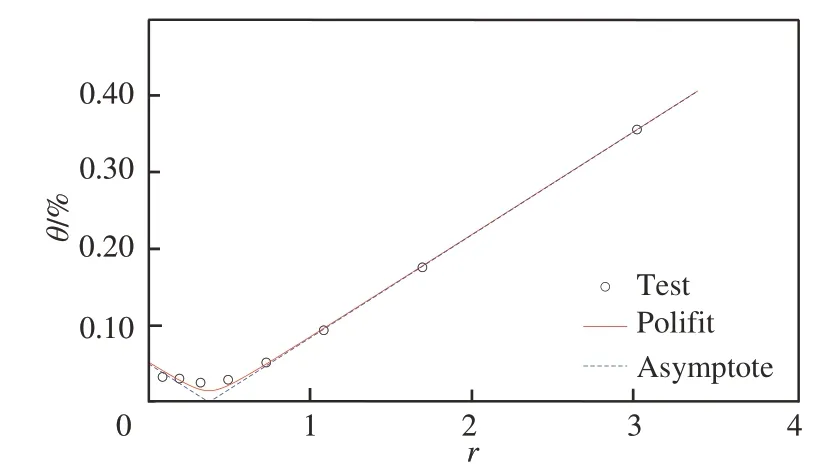
图4 马赫数0.80 流场涡模态扰动Fig. 4 Vorticity mode fluctuation at Ma=0.80
图5为马赫数0.20~1.50 流场扰动模态图的简图序列,所测结果基本可以归结为上述3 种特征图,而且,随着流场马赫数由低到高变化,扰动模态图按照“直线-双曲线-折线-双曲线-直线”的规律变化,即马赫数0.20、0.30、0.40 为直线,马赫数0.50、0.60、0.70 为双曲线,马赫数0.80、0.90、0.95 为 折 线,马 赫 数1.00、1.10、1.20、1.30 为双曲线,马赫数1.40、1.50 为直线,总体呈现较强的规律性,也反映了流场随速度逐渐提高的渐变性客观规律。
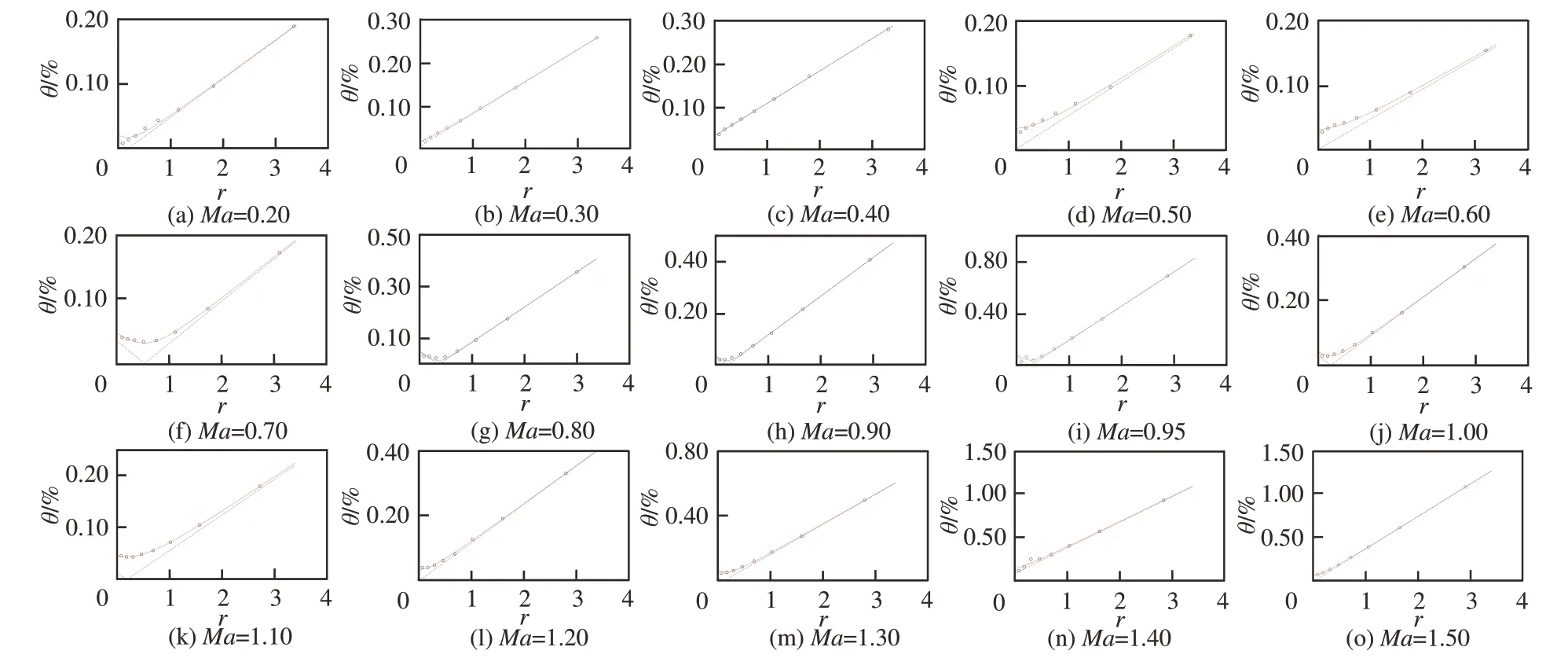
图5 马赫数0.20~1.50 流场扰动模态Fig. 5 Schematic flow fluctuation at Ma from 0.20 to 1.50
试验测得的特殊扰动模态有直线和V 形折线2 种曲线形态,结合流场参数测量结果和扰动方程特征可分析主导扰动的模态类型。根据式(12)、式(35)和式(36)获得的流场参数测量结果见表1。
图3的马赫数0.4 流场扰动曲线为直线特征,由2.4 节和2.5 节的分析可知,直线特征对应的扰动模态有熵模态和声模态2 种可能,由表1可见,马赫数0.40 的流量脉动量比温度脉动量大1 倍多,因此,图3 不可能是熵模态,只能是声模态,而且根据2.5 节的分析,由声模态的直线特性可知,声波主要来自试验段下游,应该是试验段下游弯刀支架和附面层噪声前传所致。文献[5]前期对本文风洞试验段噪声的测量结果表明,试验段下游噪声明显大于上游,印证了本文声扰动主要来自试验段下游的测量结果。
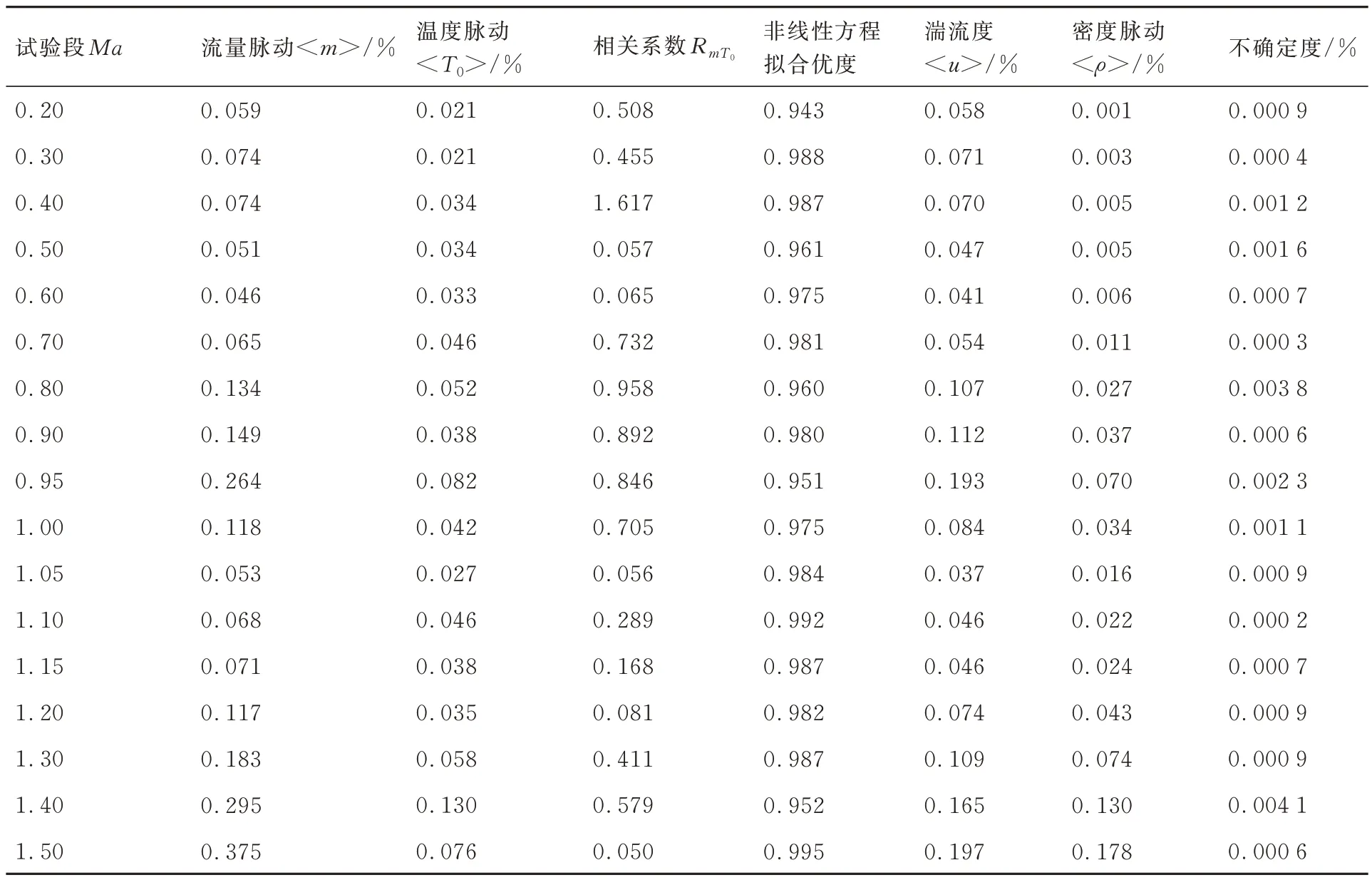
表1 流场参数测量结果Table 1 Measurement results in flow field test
图4 的马赫数0.80 流场扰动曲线为V 形折线,由2.3节和2.5节的分析可知,V 形折线对应的扰动模态有声模态和涡模态2 种可能。由式(13)可计算出β值为0.228,刚好在图4 折线的折点位置,又由2.3 节的分析,由于所测折线的折点在X轴上r=β的位置,因此可判断图4是涡模态。
由表1 流量与总温脉动量的相关系数RmT0值可见,仅有马赫数0.40 的RmT0值达到1.000 以上,说明马赫数0.40 实测值的脉动量已经转变为脉动量主导的扰动,因此是完全的声模态,拟合曲线是严格的直线。流场其他马赫数的RmT0值均小于1.000,例如马赫数1.50 的RmT0值也小于1.000,因此其扰动模态图(见图6)虽然接近于直线,但不是严格的直线,其接近X轴的线段有曲线特征。
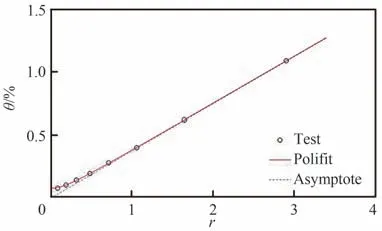
图6 马赫数1.50 流场扰动模态Fig. 6 Fluctuation mode at Ma=1.50
流场脉动量随马赫数变化趋势见图7。由表1 和图7 可见,在马赫数0.20~1.50 的范围,实测湍流度为0.037%~0.197%,总体湍流度水平较低,但是流场脉动量随着马赫数上升呈现波段上升,在马赫数0.40、马赫数0.95 和马赫数1.50 时有3 个波段高点。由图3、图5、图6 可见这3 个马赫数状态的扰动模态曲线为直线或者折线,由特殊扰动模态方程式(16)、式(20)和式(30)的特性可知,导致拟合曲线是折线或者直线的原因,应当是其中一种流场扰动量极突出占据了主导,出现流场扰动的波段峰值。在马赫数0.60 和马赫数1.10 有2 个波段低点,由图5 可见这2 个马赫数状态的扰动模态曲线为双曲线,由一般扰动方程特征式(12)可知,双曲线为一般扰动模态,此时流场中无突出扰动量,出现流场扰动的波段低点。此外,图5 中扰动曲线表现为双曲线的马赫数0.50、0.60、0.70、1.00、1.10、1.20、1.30,由图7 可见其流场流量脉动与温度脉动量较接近,而其他马赫数的特殊扰动模态流场的流量脉动明显大于总温脉动量,符合一种扰动主导时,流场扰动模态的规律发生变化。
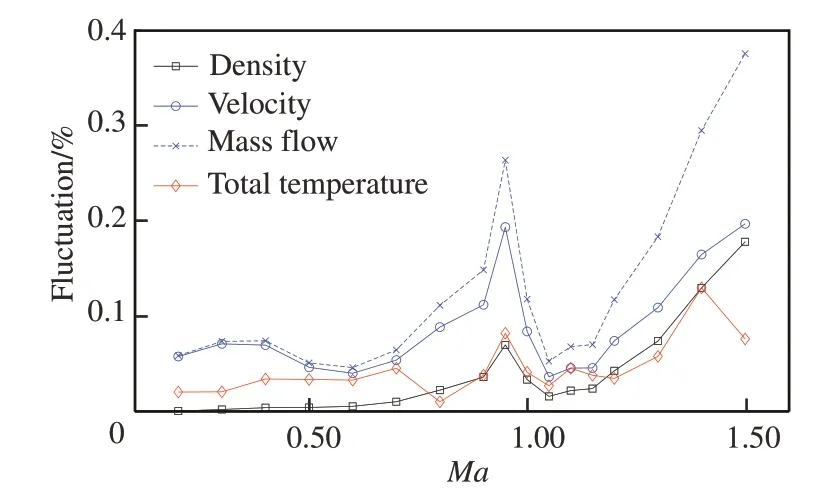
图7 流场脉动量随马赫数变化趋势Fig. 7 Fluctuation quantities at different Mach numbers
由以上分析可见,流场扰动方程与流场扰动图特征吻合,流场扰动图特征与流场试验条件、脉动量发展趋势吻合,流场扰动模态图反映了流场扰动特征。
3.2 流场频谱与流场扰动模态
当RmT0值小于1.000,扰动图又接近于特殊扰动图特征时,说明该流场大部分扰动是特殊模态,但是同时还存在其他模态的局部扰动,实际上,可压流场中极少仅有单纯一种扰动量,大部分流场同时存在速度脉动、静压脉动和温度脉动,从流场频谱的特定频率区域可以分析其主要扰动特征。
图8 是马赫数1.50 流场的热线电压脉动信号的频谱图,由图可见,信号频谱能量从低频向高频呈现指数衰减,符合自由射流的湍流耗散特征。
采用5 kHz高通频域滤波器进行滤波,对滤波后的信号再作扰动模态,得到图9,可见高通滤波后的扰动模态在接近X轴的部分也是直线,是完全的声模态扰动,说明该流场中的声扰动主要存在于原信号的高频区域,是超声速流动引起的高频声波脉动。这也引证了许多高速风洞随流速提高而噪声增大和刺耳的特点,这种噪声对气流速度产生了扰动。由图7 可见,在马赫数1.00 以后,流场湍流度随着马赫数提高也不断增大。
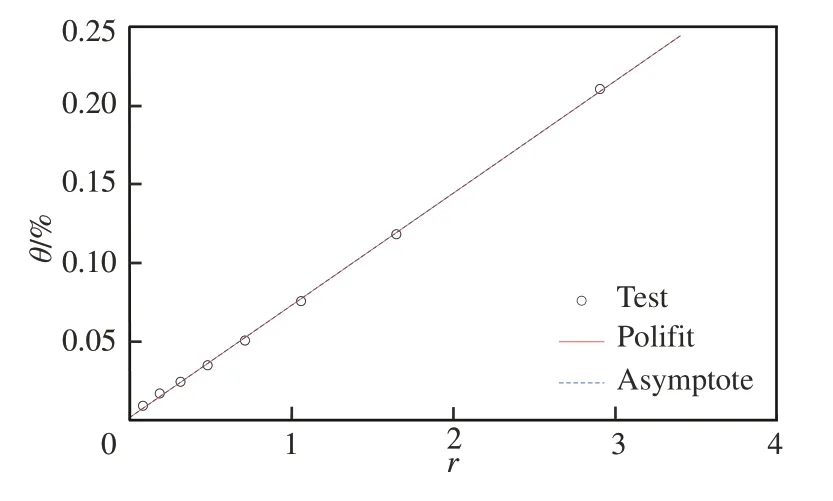
图9 马赫数1.50 流场5 kHz 高通滤波扰动模态Fig. 9 5 kHz high pass filtered signal fluctuation at Ma=1.50
3.3 数据拟合优度和不确定度
由图5 可见,扰动图拟合曲线主要为非线性特征,因此,为评估热线信号扰动模态方程与试验数据的拟合程度,统一按照非线性方程计算拟合优度。
式中:G表示曲线拟合优度;z表示实测值;z*表示预测值。
非线性拟合优度计算结果见表1,数据非线性拟合优度为0.943~0.995,说明实测数据与预测值吻合度较高。按照蒙特卡洛模拟方法[21],以实测值与预测值的差值为标准偏差,按正态分布随机产生1 000 组数据,进而计算湍流度的测量不确定度(见表1),蒙特卡洛模拟不确定度为0.000 2%~0.004 1%,在马赫数1.05 测得流场最低湍流度0.037% 对应的标准不确定度为0.000 9%,可见不确定度比湍流度低2 个数量级,说明测量结果可靠性较高。
3.4 试验误差与优化
针对实际测量中可能存在的误差,可采用蒙特卡洛模拟方法[21]和分析扰动曲线的拓扑形态,去掉误差较大的个别测点,以降低试验误差对测量结果的影响。
例如图5 中马赫数1.40 的扰动曲线,第3 个测点(过热比0.3)与扰动曲线预测值的相对误差达22%,按照蒙特卡洛模拟方法[21],以实测值与预测值的差值为标准偏差,按正态分布随机产生1 000 组数据,得到1 000 条模拟测量的扰动曲线,见图10,可见模拟扰动曲线的形态取决于误差的大小和误差点的位置。由于测点3 靠近Y轴一侧,因此对总温脉动测量结果影响较大,总温脉动模拟测量误差可达20%,但是对湍流度测量结果影响不大,湍流度模拟测量误差为2.5%。
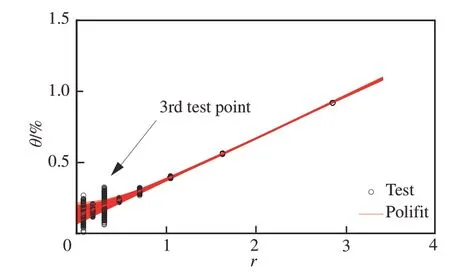
图10 马赫数1.40 流场蒙特卡洛模拟扰动曲线Fig. 10 Monte Carlo simulation for fluctuation diagram at Ma=1.40
若去掉测点3,按照蒙特卡洛模拟方法[21]再次随机产生1 000 条模拟测量扰动曲线,见图11,由于去掉了测点3,模拟扰动曲线重合度增加,总温脉动模拟测量误差降低至10%,湍流度模拟测量误差降低至0.9%。

图11 无测点3的马赫数1.40流场蒙特卡洛模拟扰动曲线Fig. 11 Monte Carlo simulation for fluctuation diagram at Ma=1.40 without the 3rd test point
4 结 论
1)从理论上推导了变热线过热比测量跨声速可压流场扰动的一般模态和3 种特殊模态特征方程:涡模态、熵模态和声模态,以及扰动模态的特征曲线。建立了利用扰动图特征和流量总温脉动相关系数等参数分析流场扰动模态的方法。
2)在流场速度为马赫数0.20~1.50 的范围内,通过试验测量获得的一般模态、涡模态和声模态扰动特征图,与流场试验条件、脉动量发展趋势吻合,湍流度0.037%~0.197%,优于设计指标,对流场评估、优化和飞行器低湍流试验有重要意义。
3)采用特征方程与扰动图分析了跨声速风洞中声模态的声波传播方向,采用频域扰动图分析方法探讨了马赫数1.50 的流场声模态扰动机理,对跨声速风洞噪声与湍流度耦合流动机理研究具有借鉴意义。
4)采用非线性方程拟合优度评估了试验数据拟合效果,并采用蒙特卡洛模拟方法计算了标准不确定度指标,不确定度比湍流度低2 个数量级,说明测量结果可信度较高。
