单桩基础弱化对海上风机动力响应的影响
2023-03-27席义博龚优华潘嘉宁王振宇
席义博,龚优华,潘嘉宁,王振宇
(1.浙江大学 建筑工程学院,浙江 杭州,310058;2.中国广核新能源控股有限公司,山西 太原,030000)
单桩基础是目前海上风机应用最广泛的基础型式[1],通过采用较大直径的钢管桩,将其打入到足够的深度以承受设计载荷。单桩支撑的海上风机是典型的高柔性结构,且由于结构服役环境复杂恶劣,对基础的性能提出了高要求。对于在役风机,桩周土体刚度退化和塑性应变累积[2-4]、土体液化[5-6]、桩基础周围局部冲刷[7-9]都将导致风机基础刚度削弱,严重降低基础的服役能力,不利于风机长期运行。
考虑桩土作用是海上风机结构分析需要关注的问题之一[10-11]。ⅤATANCHIAN 等[12]以NREL 5 MW风机为例研究了桩土作用对地震激励下的风机响应的影响,认为在模型中考虑桩土作用十分必要。ABDELKADER 等[13]针对NREL 5 MW 风机的缩尺模型进行了风洞试验,测试作用在基础上的风致荷载,结果表明,考虑基础的柔度会降低基础荷载,而刚性基础假定会导致基础荷载较为保守。PAⅤLOU[14]提出了考虑土体柔度和惯性的海上风机土体-结构-波浪相互作用的半解析模型。
土体在长期循环荷载或地震荷载作用下性状会发生改变,CHENG等[15]开展了侧向循环加载条件下黏土中考虑土体循环特性的大直径海上风机单桩基础响应的有限元分析,发现土体的强度和刚度随着循环加载次数增大而退化。ACHMUS等[16]基于一种土体的退化刚度模型评估了单桩基础在水平循环荷载下的累积变形。ISHIHARA等[17]认为基础阻尼受土体刚度影响较大。PATRA 等[18]研究了地震参数对可液化土体中单桩支撑的海上风机动力响应的影响,讨论了在风-浪-地震联合作用下的响应。LIN等[19]基于模型试验发现调谐质量阻尼系统对土体液化的海上风机仍能起到振动控制的作用。DEPINA等[20]在考虑了土体刚度退化的条件下评价了单桩在循环加载下的长期响应,随着加载次数增加,响应的均值和方差不断增大。
局部冲刷不仅导致土体对基础约束不足,还会导致基础的模态发生改变,CHEN等[21]提出了一种基于模态识别的冲刷深度预测方法,发现基础的自振频率随着冲刷深度加深而较小。TANG等[22]研究了考虑冲刷作用的海上风机动力特性,发现冲刷作用对塔筒、基础、叶片的振型均会产生影响。REZAEI 等[9]以NREL 5 MW 风机为例,基于梁单元的有限元模型分析了局部冲刷对单桩基础疲劳寿命的影响,认为冲刷作用会显著降低基础的疲劳寿命。
目前已有研究中在考虑基础刚度弱化时多数针对基础或土体本身,对基础弱化条件下的风机整体响应分析仍然较少。通常,在采用风机结构计算软件分析固定式风机时假定基础在地面完全固定,并不考虑基础与土体间的相互作用,也无法考虑基础刚度弱化的影响。本文作者以某单桩基础的海上风机为例,首先在FAST(fatigue aerodynamics structures turbulence,FAST)软件中建立起能够考虑桩土相互作用的风机结构模型,并确定桩土系统所提供的基础刚度,进而通过选取不同的基础刚度以建立不同基础弱化程度的风机结构模型。最后在FAST软件中对各个模型开展整体动力响应计算,分析风机基础和塔筒的变形、振动、载荷及疲劳特性,从而评估基础刚度弱化对风机结构动力响应的影响。
1 基础刚度模型
桩土相互作用可采用表观固定法(apparent fixity,AF)、耦合弹簧法(coupled springs,CS)、分布弹簧法(distributed springs,DS)模拟[23]。表观固定法将桩土系统等效为泥面以下的一段虚拟悬臂梁,基础刚度由该虚拟段提供;耦合弹簧法将桩土系统等效为泥面处的一组耦合弹簧,弹簧刚度即为基础刚度;分布弹簧法即p-y曲线法,沿桩深度方向布置若干水平弹簧,用以模拟桩土相互作用。表观固定法和耦合弹簧法是对p-y曲线法的有效简化,文献[24]指出三种方法具有较好的一致性,其中表观固定法计算简便,因此本文采用该方法模拟基础刚度。
表观固定法中,泥面以上仍为真实单桩,泥面以下的单桩由底部固定的虚拟桩代替,如图1所示,其长度与刚度由变形(挠度、转角)和载荷(弯矩、剪力)条件共同控制。将虚拟桩视作悬臂梁,其自由端作用有水平集中力F和弯矩M,在荷载作用下自由端产生挠度u和转角φ,即单桩在原桩土系统中泥面处的位移和转角。挠度u和转角φ表示为[23]:

图1 基础刚度计算模型Fig.1 Calculation model of foundation stiffness
式中:L为虚拟桩的长度;EI为虚拟桩的抗弯刚度。
由式(1)和式(2)求解出虚拟桩的长度L和抗弯刚度EI,由式(3)和式(4)表示,其中L取两者之中大于零的值[23]:
当采用泥面等效刚度矩阵描述桩土系统时,桩土关系由下式表示:
以上便建立起表观固定法和耦合弹簧法的等效关系,即可得到虚拟桩在泥面处的等效刚度矩阵K:
2 风机叶轮荷载
叶素动量理论是计算风机叶轮荷载的有效方法,该方法能够满足工程设计的精度要求,且不需要耗用过多的计算资源。叶素动量理论将风机叶片沿展向离散为若干个叶素,并假定各叶素间相互独立,通过求解每个叶素上的作用力,沿叶片展向积分得到作用在整个叶轮上的作用力。这种方法将每个叶素看作不考虑厚度的二元翼型,并且认为每个叶素上的作用力只由翼型的升阻特性决定。叶片截面所遇到的相对速度w看作是轴向速度va和切向速度vt的合成,如图2所示。由动量理论得到的风机叶片上dr范围内的水平推力Tb和转矩Mb为[25]:

图2 叶素受力示意图Fig.2 Blade element stress diagram
式中:ρ为空气密度;u0为无穷远来流风速;a为轴向诱导因子;a1为切向诱导因子;Fb为叶尖损失修正系数。
空气流动对叶素产生的作用力可以分解为两个方向,即垂直于相对速度方向的升力L,平行于相对速度方向的阻力D(合力为R):
式中:c为叶素截面的弦长;Cl为升力系数;Cd为阻力系数。
将升力L和阻力D投影到与叶轮平面垂直方向的PN和相切方向的PT,则有:
式中:φ为入流角,为桨距角θ和攻角α之和。
由于PN和PT是单位长度上的力,所以厚度dr上水平推力Tb和转矩Mb分别表示为:
式中:B为叶片数量。
将式(13)和(14)分别代入式(15)和(16)中,则有:
联立由动量理论得到的水平推力和转矩,即可得到轴向诱导因子a和切向诱导因子a1,采用迭代法求解诱导因子,进而得到叶轮出的水平推力和转矩。
3 等效疲劳荷载
风机在运行中受疲劳荷载作用十分突出,疲劳是结构设计的主要控制指标之一。在风机结构设计中,常用等效疲劳荷载(damage-equivalent load,DEL)来评价疲劳荷载,并可以此大致评估结构的疲劳损伤。利用等效疲劳荷载的概念可以将交变的荷载等效为一常幅荷载,可以直观地描述荷载的疲劳属性。等效疲劳荷载可由雨流计数法计算,通过雨流计数法统计荷载时程的循环次数,得到不同荷载水平的幅值和循环次数。之后指定一个或多个S-N曲线斜率m和频率f,可以得到一组固定频率f下的正弦波曲线,等效疲劳荷载的计算公式为[26]
式中:PDEL为等效疲劳荷载;ni为在荷载幅值为SRi情况下的循环次数;T为原始时间序列的持续时间。
4 实例分析
4.1 模型基本条件
算例模型中风机选择IEA 3.4MW 风机,基本参数如表1所示。地质条件选自我国东海某海上风电场,水深为9.6 m,泥面以下分别为①粉砂、②淤泥质粉质黏土夹粉土、③粉砂。单桩基础直径DP=5.5~6.0 m,壁厚tP=70 mm,长度Lp=79 m,其中泥面以下的埋入深度为55.4 m,持力层为③粉砂层。塔筒为一变截面钢塔筒,长度为73 m,塔底在静水面以上14 m处,轮毂高度为87 m。
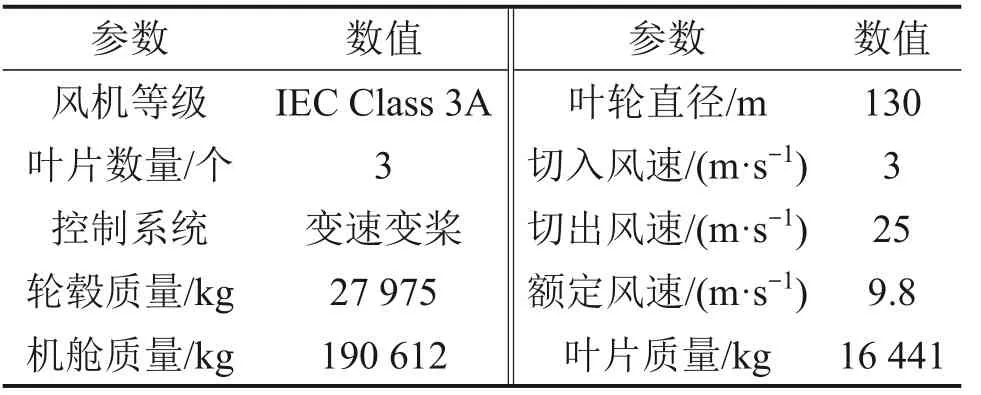
表1 算例风机基本参数Table 1 Basic parameters of example wind turbine
依据地质条件参数与单桩基础设计荷载,基于p-y曲线法计算出单桩泥面处的位移和转角,由式(3)计算出虚拟桩的长度L为28.72 m,代入式(8)得 到 泥 面 等 效 刚 度 矩 阵K=以泥面等效刚度矩阵中的平动刚度Kuu作为基准,分别取0.9Kuu、0.6Kuu和0.3Kuu三种情况以考虑不同程度的基础刚度弱化,并计算对应的虚拟桩长度。
采用BModes软件[27]计算结构的自振频率,结果如表2所示。从表2 可见:风机结构在SS(sideside)方向的自振频率高于FA(fore-after)方向的自振频率。随着基础刚度下降,结构的柔性增大,自振频率基本呈下降趋势。其自振频率会接近风机1P频率,可能会诱发结构共振的不利影响。

表2 风机结构自振频率Table 2 Natural frequency of wind turbine
采用TurbSim软件[28]模拟风速场,脉动风谱选择Kaimal 谱,轮毂处平均风速分别取9.8,12.0,15.0,18.0,21.0和24.0 m/s共6种情况。海浪采用Pierson-Moskowitz谱模拟,有效波高Hs=4.0 m,谱峰周期Tp=9.4 s。分别取Kuu,0.9Kuu,0.6Kuu和0.3Kuu共4 种基础刚度对应的虚拟桩长在FAST 软件中建立风机模型。在FAST软件中分别进行共6×4=24 种工况的计算,每个工况计算时长为660 s,进行动力响应分析。为避免初始时刻导致的瞬时不稳定响应,响应结果输出后取后600 s 时程进行分析。
4.2 基础弱化对单桩和塔筒变形的影响
变形是风机结构设计的控制指标之一,结构的过大位移容易诱发风机整体倾覆。提取各工况下结构在泥面、桩顶(塔底)、塔顶三个位置FA 方向的最大水平位移,结果如图3~5所示。由图3~5可见基础刚度对单桩水平位移具有显著影响,随着基础刚度降低,单桩在泥面和桩顶处的水平位移均呈现出增大趋势。泥面最大水平位移出现在基础刚度为0.3Kuu、风速为9.8 m/s时,泥面最大水平位移为49.4 mm。相比单桩的水平位移,基础弱化对塔顶水平位移的影响较为有限,图5中只有当风机处于大风速(24 m/s)时,塔顶水平位移会明显随着基础刚度降低而增大,而当其他风速条件时,塔顶水平位移对基础刚度的变化并不敏感,甚至可以忽略不计。此外,风机结构位移同时受风速影响,当风速处于额定风速(9.8 m/s)时,结构水平位移最大。这是由于风机存在变桨操作,在正常运行工况下额定风速时荷载最大,超过额定风速后变桨操作会降低结构荷载。风速对风机水平位移的影响随着结构高度增大而增大,塔顶水平位移受风速的影响最大,而泥面水平位移受风速的影响较小。

图3 单桩泥面最大水平位移Fig.3 Maximum horizontal displacement of monopile mudline

图4 桩顶最大水平位移Fig.4 Maximum horizontal displacement of monopile top

图5 塔顶最大水平位移Fig.5 Maximum horizontal displacement of tower top
4.3 基础弱化对塔筒振动的影响
风机结构在风、浪等动力荷载的作用下始终处于振动状态,过大的振动对结构安全十分不利。为讨论基础刚度弱化对振动的影响,提取每种工况下的桩顶FA方向加速度时程,选用均方根作为振动加速度响应的评价指标,结果如图6所示。从图6 可见:塔顶振动主要受风速影响,风速越大,塔顶加速度越大。塔顶振动加速度随着基础刚度降低而增大,但增大的程度十分有限。可见,当基础刚度存在弱化且风机在大风速条件下运行时,对于结构振动具有不利影响。

图6 塔顶振动加速度均方根Fig.6 Root mean square of tower top vibration acceleration
4.4 基础弱化对塔筒荷载的影响
风机运行时主要在FA 方向承受荷载,提取各工况下塔底FA方向的最大弯矩,结果如图7所示。从图7可知:额定风速附近时塔底弯矩最大,由于风机存在变桨操作,荷载并不会随着风速增大而增大。塔底最大弯矩受基础刚度变化的影响较小,只有当风速为24 m/s 时,塔底最大弯矩会随基础刚度降低而明显增大,对于其他风速,基础刚度降低会较小幅度地增大塔底最大弯矩,但影响程度有限。
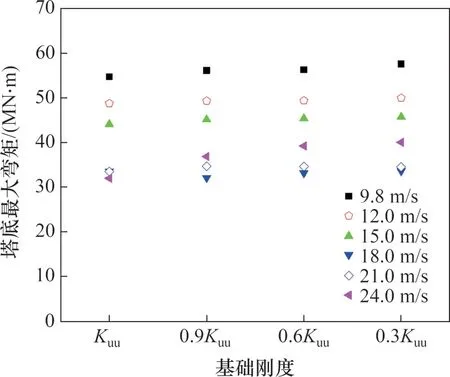
图7 FA方向塔底最大弯矩Fig.7 Maximum bending moment of tower bottom in FA direction
海上风机在服役期间持续受到循环荷载作用,极易产生疲劳损伤,结构疲劳强度是需要特别关注的指标。以等效疲劳荷载作为评价指标,讨论基础刚度弱化对结构疲劳的影响。提取各工况下塔底FA 方向弯矩的等效疲劳荷载,结果如图8所示。图8中,随着基础刚度降低,塔底弯矩的等效疲劳荷载增大,可见基础刚度弱化将引起对结构疲劳的不利影响。当轮毂处平均风速为24 m/s时,塔底弯矩的疲劳荷载最大。综合以上结果可见,相比瞬时的最大弯矩,塔筒的疲劳对基础刚度变化更加敏感。

图8 FA方向塔底弯矩的等效疲劳荷载Fig.8 DEL of tower bottom bending moment in FA direction
4.5 紧急停机工况下基础刚度对风机动力的响应
风机在运行过程中出现故障、极端环境条件等情况时会进行紧急停机操作,紧急停机工况是需要特殊关注。以轮毂处平均风速为12 m/s 条件为例,进行风机在进行紧急停机操作下的结构响应计算。假定在计算时长中第460 s 时进行紧急停机操作,包括在模型中设置关闭发电机以及叶片开始顺桨。得到泥面处水平位移结果如图9所示。图9中,当基础刚度为Kuu时,在紧急停机操作下,泥面水平位移在瞬时出现明显下降,由于风机已经停机且叶片顺桨,泥面水平位移均值下降至0附近变化,并且泥面水平位移的变化范围比停机前的大,但泥面最大水平位移仍比停机前的小。当基础刚度下降时,泥面水平位移的变化规律与基础刚度完好时类似,但紧急停机后泥面水平位移的变化范围增大,特别当基础刚度为0.3Kuu时,紧急停机后的泥面最大水平位移仍可达到停机前的水平。风机紧急停机工况时塔顶水平位移如图10所示。与泥面水平位移类似,紧急停机操作会使塔顶位移在较大范围内变化。当基础刚度下降时,紧急停机操作初期,塔顶水平变化较剧烈,一定时间后塔顶水平位移逐渐到达较稳定范围内,且基础刚度下降越大时,位移稳定所需的时间越长。塔底FA方向弯矩结果如图11所示。从图11可见紧急停机时塔底弯矩瞬时降低,紧急停机操作后,塔底弯矩均值显著比紧急停机前的小,但塔底弯矩的变化范围比紧急停机前的大,即均值降低但峰值增大。由于结构疲劳主要受循环荷载的影响,紧急停机会增大结构的疲劳。当基础刚度下降时,会进一步增大塔底弯矩的峰峰值,更加剧结构疲劳损伤的风险。

图9 不同基础刚度下的泥面水平位移Fig.9 Horizontal displacement of monopile mudline at different foundation stiffness
图10 不同基础刚度下的塔顶水平位移Fig.10 Horizontal displacement of tower top at different foundation stiffness

图11 不同基础刚度下的塔底FA方向弯矩Fig.11 Bending moment of tower bottom in FA direction at different foundation stiffness
4.6 讨论
本文是以IEA 3.4MW 风机为研究对象,对于更大装机容量的海上风机,仍可采用本文技术路线。当采用更大直径单桩基础时,传统p-y曲线难以考虑桩基础尺寸效应,导致低估基础承载力,因此需要对大直径单桩的p-y曲线进行改进[29-31]。此外,本文是针对软黏土场地条件讨论了基础弱化,当场地条件不同时,如砂土场地时,桩周砂土在长期循环荷载作用下可能会更加密实,使得基础出现强化现象[32-33],需要根据具体条件进一步分析。
5 结论
1)基础刚度弱化会降低风机结构的自振频率,使其接近风机的1P频率,可能会诱发结构共振。
2)基础刚度弱化会明显增大单桩基础的水平位移,而塔顶位移受基础刚度变化的影响较小,塔顶水平位移主要受风速影响。
3)塔顶振动加速度随着基础刚度弱化而轻微增大,塔顶振动主要受风速影响,风速越大,塔顶振动越剧烈。
4)基础刚度降低会增大塔底疲劳荷载,导致对结构疲劳承载力产生不利影响,基础刚度降低对极限荷载的增加影响相对较小。
5)在风机进行紧急停机操作时,基础刚度的变化对结构动力响应的影响十分明显,基础刚度下降会使各响应量在较大范围内变化,使结构响应变化更为剧烈,不利于结构安全运行。
