基于压力舒适性的400km/h双线高速铁路隧道净空面积研究
2023-03-27王田天吴小梅张雷钱博森陆意斌
王田天,吴小梅,张雷,钱博森,陆意斌
(1.中南大学 交通运输工程学院,轨道交通安全教育部重点实验室,湖南 长沙,410075;2.湖南大学 机械与运载工程学院,湖南 长沙,410082)
近年来,中国高铁蓬勃发展,目前最高运营速度已达350 km/h[1]。为满足人们对更高出行速度的需求,国内正在积极开展400 km/h 速度等级的高速铁路研发工作[2-3],其中一项重要研究是确定该运行速度下的隧道净空面积。确定铁路隧道净空面积时,不仅应考虑隧道建筑限界和机车车辆界限,而且要考虑列车通过隧道时诱发的空气动力学效应[4-5]。随着运行速度提升,列车隧道交会时瞬间气动载荷呈指数增大,不仅会对列车结构和隧道附属设施造成损坏,而且车外的剧烈压力波动会传入车内,冲击乘客的耳膜,引起车内人员压力舒适性的问题[6]。列车内瞬变压力的变化能否符合乘客舒适度标准是确定高速铁路隧道断面尺寸时最重要的考量因素[7]。冉腾飞等[8]对速度为140 km/h的高速地铁隧道净空面积进行了研究,发现当隧道净空面积采用现有速度为120 km/h、地铁常用净空面积26 m2时,所需地铁列车密封指数为6 s;当地铁列车密封指数取4 s和3 s时,所需地铁隧道净空面积分别为30.5 m2和35.7 m2。吴剑等[9]结合我国列车的实际密封条件和现行舒适度标准,对车速分别为120,160 和200 km/h 的城际铁路隧道净空面积予以论证,为我国城际铁路相关标准、规范的制订提供了参考依据。韩运动等[10]研究了车内压力幅值与列车速度的关系,构建了车内压力幅值与列车速度的表达式,为高速列车在隧道内运行时的安全性指标提供了压力评判依据。马瑶等[11]对速度为350 km/h 的高速列车在不同时间间隔下高速列车通过不同长度隧道时车辆自身的动态时间常数进行了探讨。研究者对列车内外压力传播机理和影响因素等也开展了研究,并基于舒适度标准对实际工程应用提出了建议。史宪明等[12]基于舒适性标准,探讨了400 km/h 高铁维持现有隧道净空断面运行的可能性。
上述对于隧道净空面积的研究大多集中于速度在350 km/h 及以下,对于速度为400 km/h 的高铁研究缺乏具体的计算方法和过程展示。本文以16 车编组高速列车为研究对象,采用数值模拟和动模型试验方法研究速度为400 km/h 的高速列车在不同净空面积隧道交会时的气动载荷,并基于现有列车气密性和压力舒适性标准对速度为400 km/h的长编组高速铁路双线隧道净空面积提出建议。
1 数值计算模型
1.1 数值模型
本研究选用16 车编组的高速列车,总长为413.2 m,模型如图1所示,不同净空面积双线隧道模型横截面如图2所示。其中,净空面积为100 m2的标准双线隧道断面高度为8.78 m,线间距为5 m[13]。净空面积分别为90,95,105 和110 m2的隧道断面参数则是由100 m2标准双线隧道断面乘以相应的系数得到。为了模拟列车隧道交会时压力波动的极端情形,本文隧道长度采用最不利隧道长度Lcritical[14],其表达式为

图1 16车编组高速列车模型Fig.1 16-car unit high-speed train model
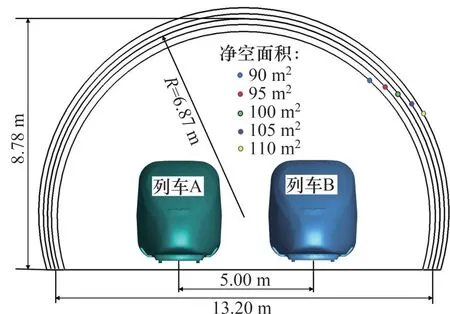
图2 不同净空面积双线隧道横截面Fig.2 Cross section of double track tunnel with different clearance area
其中:Ltr为列车长度;Mtr为列车运行速度的马赫数。由式(1)可得本研究对应的最不利隧道长度为
1 265 m。
1.2 计算区域及边界条件
图3所示为本研究的计算区域尺寸及边界设置示意图。为了保证列车进入隧道时计算域初始流场趋于稳定,开始计算时,列车均距离隧道口50 m 处[15]。采用滑移网格技术模拟列车与列车以及列车与隧道之间的相互运动[16],整个计算区域被划分为3 个不重叠的区域。其中,2 个区域为滑移域,分别包裹着列车A和列车B以速度400 km/h相向运动,其余域为静止域。滑移域与静止域的交界面定义为交换面、列车和隧道壁面,外部空气区域靠近隧道2个侧面(山体面)以及地面设置为无滑移壁面。其他区域面设置为压力出口。
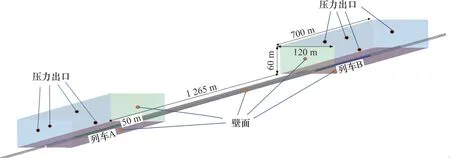
图3 计算区域和边界条件Fig.3 Computational area and boundary conditions
1.3 计算网格
计算网格如图4所示。本研究的高速列车带有转向架等复杂部件,因此,选择混合网格对计算域进行离散。将列车周围区域离散为非结构化网格,其余部分离散为结构化网格,列车表面上的最小网格边长为0.05 m,隧道壁上最小网格边长为0.2 m。在隧道净空面积分别为90,95,100,105和110 m2工况下,网格总数分别为6 790万、6 798万、6 888万、6 984万和7 088万个。
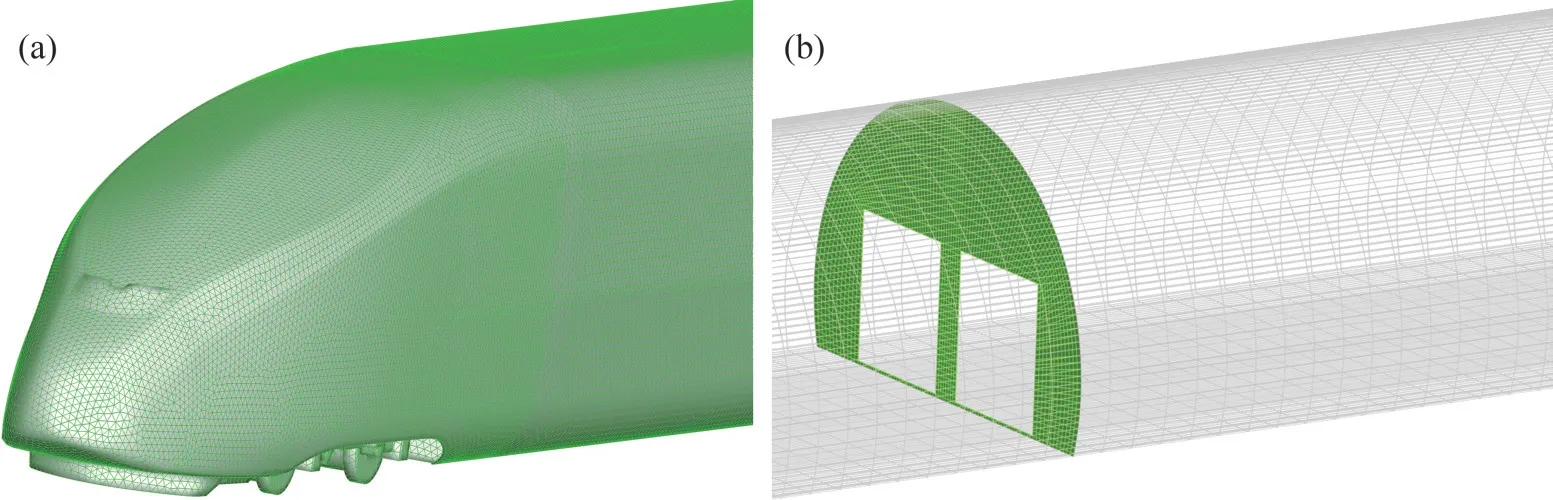
图4 计算网格Fig.4 Computational grid
1.4 求解设置
本研究选用的求解软件为FLUENT,这是一款基于有限体积法的商用求解器。列车在隧道内运行时,由于空气受到隧道和车体壁面的影响,空气应视为可压缩气体[17]。考虑到列车与隧道间的空气受到摩擦和传热等影响,气流为不等熵流动,因此,采用非定常、黏性、可压缩流的N-S方程来求解列车过隧道的流场。k-ε湍流模型目前广泛应用于列车通过隧道时的数值模拟[18],其中,RNGk-ε湍流模型引入了时均应变率,从而能提高列车流场求解的准确性和可靠性,且与试验结果有更高的吻合度[19],因此,本文选用RNGk-ε湍流模型求解。求解速度和压力的耦合方式选用SIMPLE算法,基于格林高斯的单元法用来控制梯度变化,二阶迎风格式用于离散对流相[20]。为了保证滑移网格每步移动的距离不会影响计算速度和可靠性,设置每步的时间为0.007 5 s,内迭代50次[21]。
1.5 测点布置
列车模型部分测点布置如图5所示,头车分布12个测点,分别记为分别H1,H2,…,H12。中间车每节车外表面分布8个测点,14节中间车外表面共112 个测点,分别记为M13,M14,…,M124。尾车与头车前10 个测点分布一致,后2 个测点分别距离尾车鼻端点3.3 m和5.1 m,并位于列车中心面上,分别记为T125,T126,…,T136,16节车共布置136个测点。
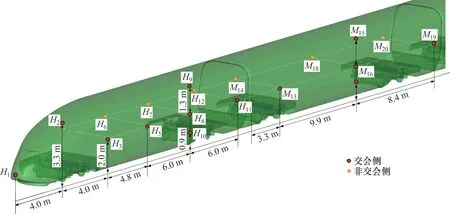
图5 列车表面测点Fig.5 Train surface measuring points
2 数值验证
2.1 动模型试验
中南大学轨道交通安全教育部重点实验室的动模型试验平台可使橡胶弹射使模型动车组在模型线路上无动力高速运行,能准确模拟两动车组在隧道中的交会过程。为了对本文采用的16 车编组隧道交会的数值方法可靠性进行评估,在此平台上展开速度为400 km/h 的高速列车隧道交会的动模型试验。在进行模型实验时,为了有效模拟实车在线路上运行的实际情况,使测试数据具有真实性,应确保一些重要的相似性参数在模拟试验和实车试验中一致。对于动模型实验,重要的相似性参数包括几何相似、马赫数相似、雷诺数相似[22]。在本次动模型试验中,前2个参数保持一致,对于后1个参数,只需保持试验中模型列车雷诺数大于等于临界雷诺数(研究表明,临界雷诺数约为3.6×105[23]),就可保证动模型试验中列车模型周围流场和产生的压力满足相似性原理和流动现象的自模性。本动模型试验选用的模型缩比为1:20,当模型列车以400 km/h 运行时,雷诺数为1.45×106,超过临界雷诺数3.6×105,模型列车已进入自模拟区。故本试验选择缩比为1:20 的三车编组列车与隧道模型较合适。本次试验共进行15 次弹射,其中,发射速度不在目标速度1%以内的工况不被选用,并采用所有选用工况的平均值为最终的试验结果。
试验选用的三车编组的高速列车模型,对应总长为82 m的实际列车。头车外表面分布12个测点,对应数值模拟的测点H1,H2,…,H12,中间车外表面分布8 个测点,对应数值模拟的M13,M14,…,M20,尾车外表面分布12 个测点,对应为T125,T126,…,T136。隧道模型对应的实际净空面积为100 m2,长度为164 m,如图6(a)所示。对比验证的数值方法采用的计算网格和求解设置分别与本文1.3 和1.4 节中的一致,数值模型为全尺寸模型。本次试验采用的Honeywell DC030NDC4压力传感器如图6(b)所示,记录高速列车通过隧道时压力随时间的变化。传感器采样频率设置10 kHz,在重复性试验中所测量的压力幅值误差在±1%以内。净空面积为100 m2的隧道壁面上的测点布置如图7所示。试验中,在隧道壁面上共布置8个测点,图7中可见的(即隧道长度的一半)隧道交会侧壁面测点数为6个,非交会侧壁面测点数(图7(a)中括号内测点)为2个,分别记为S1,S2,…,S8。

图6 试验模型及压力传感器Fig.6 The models and pressure sensor

图7 隧道壁面测点分布Fig.7 Distribution of measuring points on tunnel wall
2.2 结果比较
3车编组动车组以400 km/h于隧道交会,车体表面测点M13与隧道壁面测点S4的压力时程曲线分别如图8(a)和图8(b)所示。由于数值模拟的隧道长度是动模型试验长度的20 倍,因此,将试验的时间进行相应转换。同时,由于雷诺数大于3.6×105,模型尺寸对列车周围的流场影响很小,因此,试验测点的压力可以代表全尺寸模型的压力[15]。从图8可见:除了隧道壁面测点S4在1.2 s后动模型曲线比数值模拟曲线有所延后外,其余时间的数值计算曲线与动模型曲线都较吻合;曲线的正负压幅值之差为压力峰峰值,表1所示为列车头车测点H2、中间车测点M18、尾车测点T134以及隧道壁面测点S3。S5和S6的压力峰峰值,最大压力的数值计算结果与动模型试验结果的峰峰值之差在±3.2%之内,证明本文采用的数值方法具有较高的准确性和可靠性。

图8 数值模拟与动模型试验压力曲线对比Fig.8 Comparison of pressure curves between numerical simulation and dynamic model test

表1 数值模拟与动模型试验压力峰峰值比较Table 1 Comparison of pressure amplitude between numerical simulation and moving model test
3 结果分析
3.1 隧道压力波分析
高速列车在净空面积为100 m2标准双线隧道等速交会时的压力波动传播和隧道中间测点的压力变化如图9所示。规定列车车头驶入隧道时(t=0 s),到车尾驶出隧道整个过程持续15 s。取隧道中点处竖直方向为3 m的测点进行隧道压力波传播分析,压力波动经历了2 次上升和上次下降过程。从图9可见:列车A和列车B进入隧道时,初始压缩波在隧道中点相遇叠加导致C处压力上升;压缩波以声速沿隧道传播到隧道出口时反射成膨胀波并向隧道内传播,当该膨胀波传播至隧道中点时,与此同时,2列列车车尾进入隧道引起的膨胀波到达此处并叠加导致D处压力急剧下降,这些膨胀波以声速传播到隧道终点反射成压缩波在隧道中点叠加导致E处压力上升,这些波又反射回来导致F处压力下降。隧道长度的改变将使压力波在隧道内叠加情况发生变化,进而改变压力波的最大幅值与出现位置。本文隧道模型采用列车隧道交会时的最不利隧道长度,车头和车尾进入隧道的时间间隔恰好等于波沿隧道单程传播的时间,进而导致车头进入隧道的初始压缩波反射的膨胀波和车尾进入隧道引起膨胀波在隧道两侧同时产生且恰好在隧道中点处叠加,在隧道中点处产生最大负压,使得隧道内的气动效应最大,压力波动情况也最剧烈。
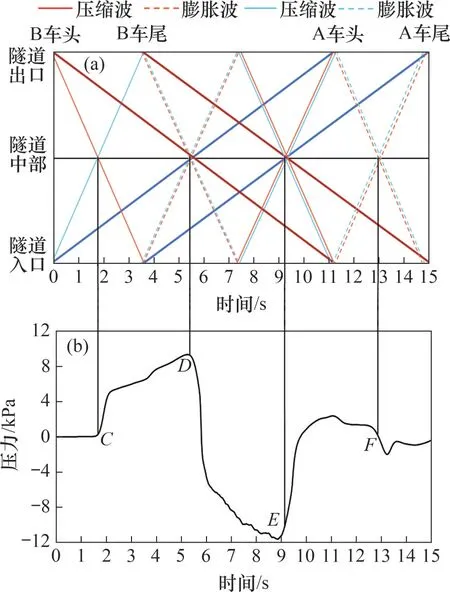
图9 隧道中部测点的压力传播图以及点压力曲线Fig.9 Pressure propagation diagram and pressure curve of measuring points in the middle of tunnel
3.2 车内外压力传递
为反映列车气密性能,常常使用密封指数进行量化[24]。密封指数分为静态密封指数与动态密封指数。静态密封指数在数值上等于车内外压差由初始值减少到初始值的37%所用的时间[24]。在试验过程中,车外的压力保持恒定,而列车在隧道运行过程中,车身经历的压力是瞬态且剧烈变化的,因此,静态密封指数无法很好地评估车内的压力波动情况。而动态密封指数能表征车外瞬变压力传递至车内的能力,可反映列车通过隧道时室内压力的变化,因此,本文选用的是动态密封指数τ。国内现无针对400 km/h列车密封性能的标准,按照相关标准,350 km/h列车的静态密封指数要求不小于50 s[25],国际铁路联盟标准规范中规定车辆动态密封指数通常仅为车辆静态密封指数的1/3~1/2[25],这样可得出350 km/h 列车的估算动态密封指数为18~25 s。由于长隧道使传递过程压力波能量产生更大衰减,隧道长度增加,列车的密封性能更好,动态密封指数升高,可达到20 s。经综合考虑,本文采用动态密封指数τ=20 s进行研究。车内部压力变化率与内外压差呈正比,与密封指数呈反比,表达式为
其中:Pi为车内部压力;Pe为外部压力;τ为动态密封指数。当列车密封指数为0即列车内外压力相等时,车内压力与车外压力同步变化。列车密封性能越好,则车内外压力平衡的速率越小,即车内的压力波动越滞后于车外的压力波动。由于2列列车速度相等,在隧道交会过程中压力波动完全对称,因此,只需分析列车A 压力波动情况。将每节车厢的测点车内外压力峰峰值取平均值得到车内和车外表面平均压力峰峰值,分别如图10(a)和图(b)所示。从图10 可以看出:随着隧道净空面积增大,车内和车外表面的平均压力峰峰值都不断减小;从头车到尾车,车外表面的平均压力峰峰值不断减小,尤其尾车处压力减小得很快;车内的平均压力峰峰值则呈现相反的趋势,尾车部位增大的较快;车内外平均压力峰峰值在从头车向尾车呈现相反的趋势,说明车内的压力波动情况不仅与车外表面压力峰峰值有关,而且与车外表面压力峰峰值的形成、持续时间以及衰减的时间有关。

图10 从头车到尾车方向列车平均压力峰峰值变化Fig.10 Peak to peak variation of train average pressure from head to tail
为了进一步探究列车内外压力传递关系,选取列车在净空面积为100 m2的双线隧道交会的情况下进行分析。以列车刚驶入隧道时刻为时间零点,到车尾驶离隧道整个过程持续15 s。分别取头车交会侧测点H3,中间车交会侧测点M40和M104以及尾车交会侧测点T134车内外压力进行对比,如图11所示。从图11 可见:车内的压力振动情况较车外平缓,压力幅值比车外约小1个数量级;列车各车厢外表面经历的压力波动有很大差异,测点H3,M40和M104都有第一个波峰,测点T134缺少第一个波峰。这是由于列车在隧道交会过程中,当列车A的尾车驶入隧道入口时,对向列车驶入隧道引起的初始压缩波已经在隧道入口反射为膨胀波反向传播,测点T134没有经历初始压缩波带来的第一次压力上升。随后,测点H3,M104,M42和T134的压力依次经历了车尾进入隧道的膨胀波引起的下降,10 s以后,车内外压力趋于平稳。
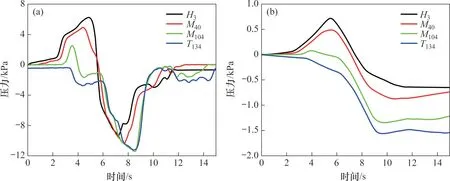
图11 列车在净空面积为100 m2隧道的交会压力曲线Fig.11 Pressure curves of train crossing in 100 m2 tunnel
3.3 隧道净空面积的影响
在不同隧道净空面积下,头车测点H3、中间车测点M64和尾车测点T134车内外压力波动曲线分别如图12~14所示。以列车刚进入隧道的时刻为零点,到车尾离开隧道整个过程持续15 s。在列车驶入不同净空面积隧道过程中,测点H3,M64和T134的车内外压力峰峰值都随着隧道净空面积增加而减小。由于隧道长度不变,不同隧道净空面积下车内外压力波动趋势一致,车内的压力波动滞后于车外的压力波动。12 s后,头车在离开隧道,测点H3车外表面压力趋近于零,车内压力稳定在-700 Pa左右。对于测点H3车外表面的第一个波峰和波谷,车内的压力都有所响应。当车外表面压力稳定即车内外压差保持不变时,车内的压力以极小的速率和车外表面压力平衡。测点M64车外表面压力经历了波峰和波谷后趋于平稳,车内压力变化趋势和车外表面的相同。测点T134车外表面压力缺少第一个波峰,在8 s 左右达到第一个波谷后迅速回升到初始值,之后又开始小幅度下降,车内压力对于第一个波谷有很好的响应,对于之后的压力迅速回升几乎没有响应,12 s后又开始稳步下降。
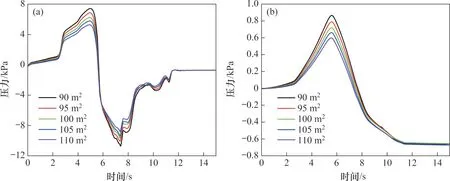
图12 测点H3压力波动曲线Fig.12 Pressure fluctuation curves of measuring point H3
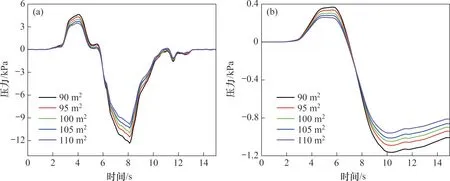
图13 测点M64压力波动曲线Fig.13 Pressure fluctuation curves of measuring point M64
表2所示为测点H3,M64和T134车内外压力峰峰值。从表2可见:相较于90 m2净空面积的隧道,列车在110 m2净空面积的隧道交会时,测点H3车外表面压力降低了29%,车内压力下降了22%;测点M64车外表面压力降低了28%,车内压力降低了16%;测点T134车外表面压力降低了25%,车内压力下降了28%。可见,头车的车外表面压力峰峰值和尾车的车内压力峰峰值受隧道净空面积影响较大。在同一个隧道净空面积下,测点H3车外压力峰峰值都大于测点T134车外压力峰峰值,而车内压力峰峰值则相反。测点H3车内压力峰峰值都小于测点T134车内压力峰峰值。产生这一现象的原因是头车车外压力2个峰值之间的幅值大,但持续的时间很短,车内压力对车外的压力波动响应不完整。而尾车车外压力未经历第一个峰值,正峰值几乎为零,因此,车外压力峰峰值比头车的小。尾车压力负峰值形成以及持续的时间很长,车内的压力响应很完整,尾车车内的压力峰峰值比头车的大。
3 s 内最大的压力波动是车内人员出现耳感不适的主要原因[26]。根据“铁路隧道设计施工有关标准补充规定”[27],当线路中隧道所占比例大于25%或通过隧道大于4座/h时,单、双线隧道对应的舒适度标准分别为800 Pa/(3 s)和1 250 Pa/(3 s)。本文研究的是16 车编组以速度400 km/h 在隧道中交会的情况,因此,选用车内压力波动幅值不超过1 250 Pa/(3 s)为基准对速度为400 km/h的高速铁路隧道净空面积进行研究。
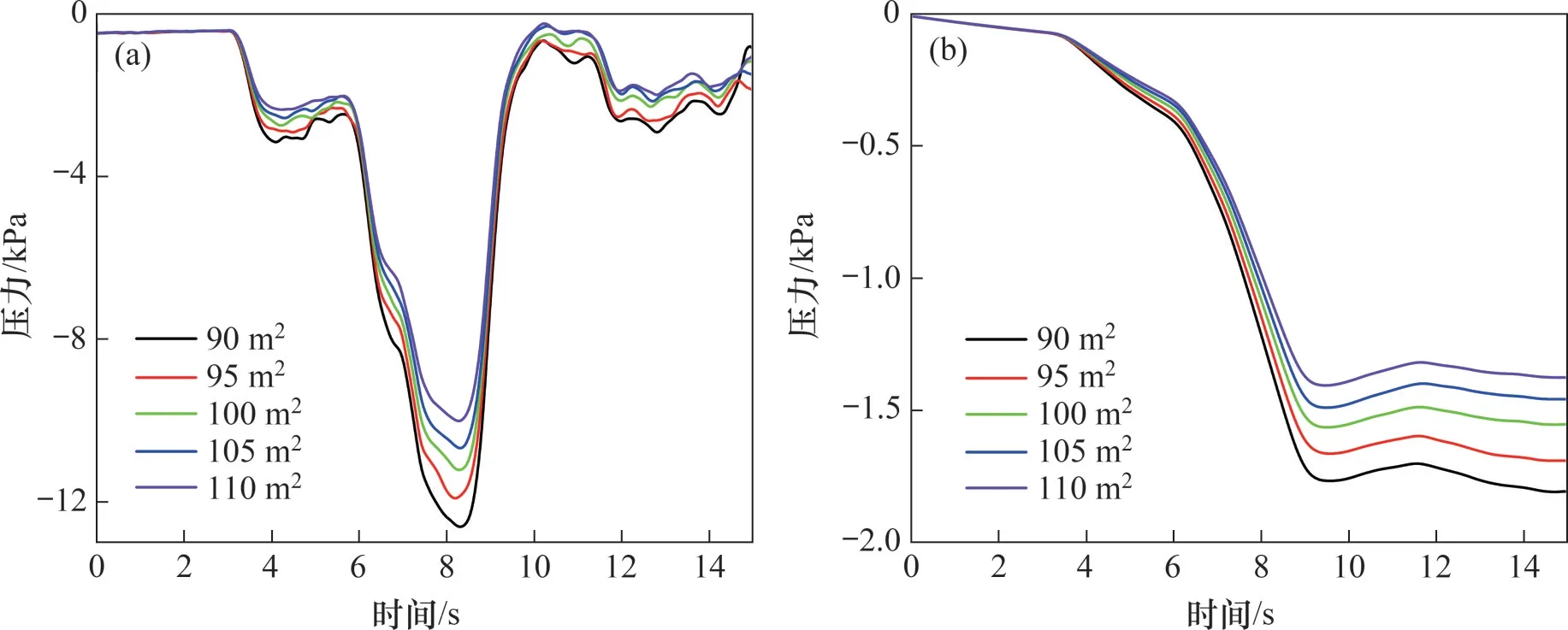
图14 测点T134压力波动曲线Fig.14 Pressure fluctuation curves of measuring point T134
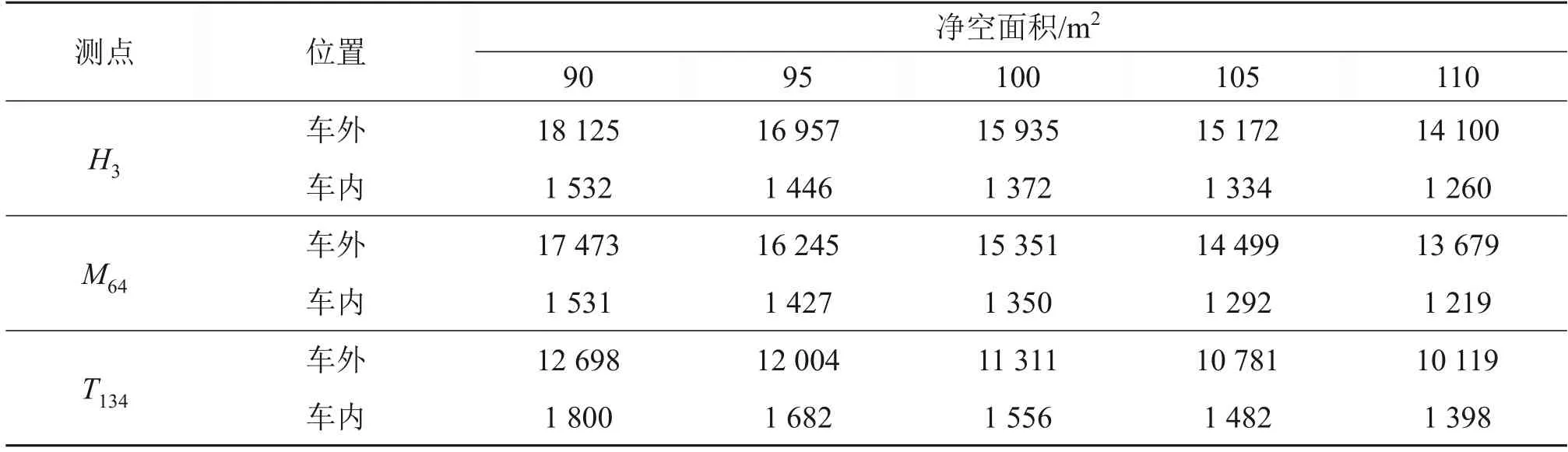
表2 不同测点车内外压力峰峰值Table 2 Comparison of pressure amplitude inside and outside the train of different measuring points Pa
图15所示为列车交会侧测点对应的3 s内车内最大压力波动幅值。从图15可见:从头车到尾车,列车车内3 s 压力波动幅值先逐渐增大又缓慢下降,在中间车测点M104达到最大值;当隧道净空面积从90 m2增加到110 m2时,各测点的压力波动幅值呈现稳步下降的趋势,测点M104的压力波动幅值从1 393 Pa 下降到1 102 Pa,下降20.9%;尾车的附近车外表面压力波动幅度较大,对气密性能要求较高。由于车体总的气密性受气密性最差的部件影响最大,可局部加强车内压力波动幅度较大、气密性较差部位的密封性能来提升车辆总体气密性。参考车内压力波动的舒适性标准,当隧道净空面积为90 m2和95 m2时,分别有15 节、10 节车厢的车内压力波动幅值超过规定舒适值,对于净空面积为100,105 和110 m2的隧道,车内压力波动都满足规定舒适值,并且对于净空面积为105 m2和110 m2的隧道,车内的压力波动幅值离舒适度标准还有较大差距。增加隧道净空面积,可以有效减少列车内压力波动,但同时也会增加隧道土建部分的建造成本。基于现有列车能达到的气密性标准,在保证车内压力舒适度的前提下,400 km/h速度等级的长编组列车推荐的隧道净空面积为100 m2。
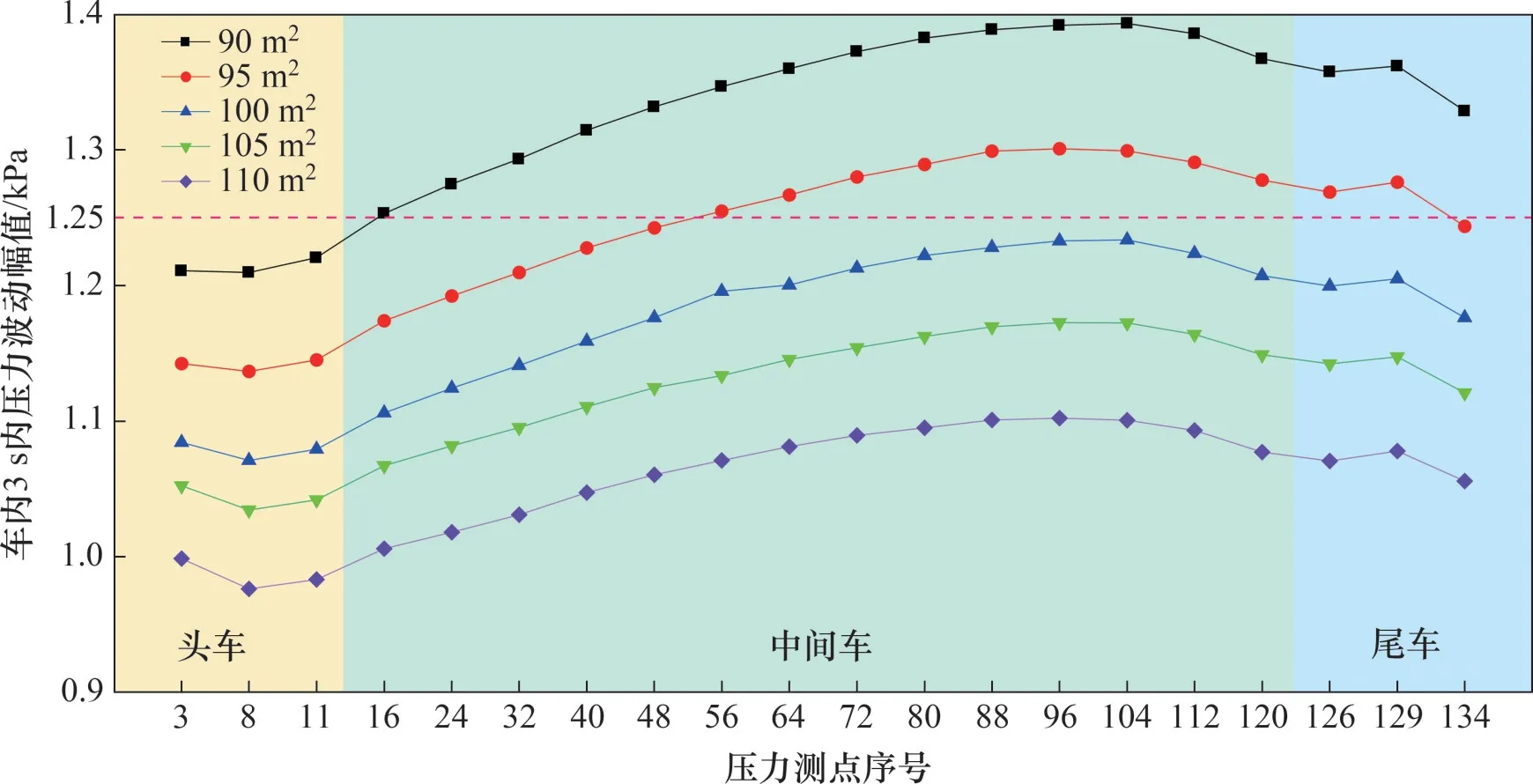
图15 不同净空面积隧道3 s内车内压力波动幅值Fig.15 Amplitude of pressure fluctuation in vehicle within 3 s in tunnels with different clearance areas
4 结论
1)16 车编组的高速列车以速度400 km/h 在净空面积为100 m2的标准双线隧道内交会时,从头车到尾车上,车外表面的平均压力峰峰值不断减小,车内的平均压力峰峰值不断增大。
2)列车在净空面积为90 m2和95 m2的隧道交会时,分别有15 节、10 节车厢的车内压力波动幅值超过规定舒适值。净空面积为100,105 和110 m2的隧道车内压力波动都满足舒适性标准,并且净空面积为105 m2和110 m2的隧道车内的压力波动幅值离舒适性标准还有较大差距。综合考虑现有高速列车气密性与舒适度标准,运行速度为400 km/h的长编组高速列车双线隧道净空面积推荐采用100 m2。
