Brittle and ductile characteristics of intermetallic compounds in magnesium alloys: A large-scale screening guided by machine learning

Russln Jfreh ,Yoo Seong Kng,b ,Kotib Hmd,∗

aSchool of Advanced Materials Science &Engineering,Sungkyunkwan University,Suwon 16419,South Korea

bSchool of Applied Data Science,Sungkyunkwan University,Suwon 16419,South Korea

Abstract In the present work,we have employed machine learning (ML) techniques to evaluate ductile-brittle (DB) behaviors in intermetallic compounds (IMCs) which can form magnesium (Mg) alloys.This procedure was mainly conducted by a proxy-based method,where the ratio of shear (G)/bulk (B) moduli was used as a proxy to identify whether the compound is ductile or brittle.Starting from compounds information (composition and crystal structure) and their moduli,as found in open databases (AFLOW),ML-based models were built,and those models were used to predict the moduli in other compounds,and accordingly,to foresee the ductile-brittle behaviors of these new compounds.The results reached in the present work showed that the built models can effectively catch the elastic moduli of new compounds.This was confirme through moduli calculations done by density functional theory (DFT) on some compounds,where the DFT calculations were consistent with the ML prediction.A further confirmatio on the reliability of the built ML models was considered through relating between the DB behavior in MgBe13 and MgPd2,as evaluated by the ML-predicted moduli,and the nature of chemical bonding in these two compounds,which in turn,was investigated by the charge density distribution (CDD) and electron localization function (ELF) obtained by DFT methodology.The ML-evaluated DB behaviors of the two compounds was also consistent with the DFT calculations of CDD and ELF.These finding and confirmation gave legitimacy to the built model to be employed in further prediction processes.Indeed,as examples,the DB characteristics were investigated in IMCs that might from in three Mg alloy series,involving AZ,ZX and WE.

Keywords: Mg alloys;Intermetallic compounds;Ductile-brittle;Machine learning;Algorithm;Features;DFT.

1.Introduction

Magnesium (Mg) and its alloys are among the most promising materials for several fields including structural and medical applications [1].This is due to its naturally abundant(2.5%),and lightweight(33%and 75%lighter than aluminum and steel,respectively) [2].In addition,Mg-based alloys exhibit both biocompatibility [3] and suitable mechanical properties [1] to be employed as implants in medical applications[4].Mechanical properties,including strength,ductility,and toughness,of Mg alloys are mainly associated with their microstructural features,such as texture,grain size,grain boundaries,and second phases,which,in turn,are evolved after the processing of these materials.Among these features,the characteristics of the formed 2nd phase intermetallic compounds are very significan as the morphology,size,and distribution of these phases can highly influenc the plasticity of the host alloy.For example,in AZ-based Mg alloys,those which basically contain Al and Zn as alloying elements,Mg17Al12phase forms in the matrix,and under specifi characteristic of size and morphology,this phase can contribute to enhance both the strength and ductility of the AZ alloy by reducing the dislocation mobility (particle-dislocation interactions) and enhancing the strength of grain boundaries [1].In addition to the previous characteristics,the mechanical nature of these compounds,whether they are ductile or brittle,is also of importance in controlling the performance of the alloy.In this regard,the mechanical properties of the Mg-based intermetallic compounds,which form in Mg alloys,are usually determined theoretically using density functional theory (DFT) calculations [5].Classically,the DFT-calculated ratio of shear (G)and bulk (B) moduli can indicate to the nature of the counterpart compound,and accordingly,it can be used as a proxy which is a distinct,quantifiabl material property that scales with ductile-brittle behavior.Using this proxy,the compounds with G/B>0.57 are brittle,whereas they are ductile when this ratio is less than 0.57,and this is known as the Pugh criterion [6].

Such elastic moduli (G and B) are intrinsic properties of compounds,and they can be accurately calculated using DFT methodology.To classify the intermetallic compounds in Mg alloys using the previous criterion,DFT calculations will be needed for every and each compound that is presents in the phase diagrams of Mg alloys.Considering the complicated,costly and time-consuming nature of the DFT method,it will be impossible to establish a ductile/brittle database solely using DFT alone.Although,DFT is a powerful tool to provide high accuracy calculations for materials moduli in most cases,up to now,this approach has been employed to calculate the elastic constants for ∼6000 crystalline materials,which is less than 1% of the known materials in this class,as calculated from AFLOW database.In this regard,the recent development in the fiel of machine learning (ML) algorithms and the proportional progress achieved in the computing capability opens the door widely in front of the accelerated materials design and discovery [7–10].This was additionally motivated by the large amount of data which are available from reported works and materials databases,like Materials Project(MP) [11],AFLOW [12],and the Open Quantum Material Database (OQMD) [13].By ML,a predicative model can be built based on previous experiences on the targeted property,and the model is employed to predict this property starting from various features that might describe the materials using their composition [14],crystal structure [15,16],microstructure,and/or processing conditions [17].

Up to here,the present work was designed to accelerate the mechanical property-based classificatio of intermetallic compounds,which are expected to form in the various series of Mg alloys,such as AZ,ZK,AM,WE,etc.,using the ML techniques.Here,the constructed proxy (G/B) for compounds that have B and G,as they are available in the open source DFT materials databases (MP,AFLOW,OQMD),is arranged,the related features of the compounds are generated,and finall this data (proxy and related features) are included in a learning process using suitable ML algorithms.The models to be reached by the present learning process,accordingly,will be used to determine the proxy of other compounds,which have no related DFT calculations,leading to an extremely extended database (>106compounds).To validate the reached ML model,this work will also be combined with first-principle calculations of some compounds form the ML-extended database that show a characteristic brittle and ductile behavior based on the aforementioned proxy.

2.Learning procedure

2.1.Initial dataset construction and dada characteristics

The initial dataset used in the present work contains the DFT-calculated moduli (G and B) and the counterpart compounds with their crystal structure information and space groups.This information was extracted from the AFLOW database [12],which is a publicly available database of 3562,831 compounds with more than 705,440,538 DFTcalculated properties,including electronic,mechanical,thermal,optical,and magnetic properties.Based on the main target of the present work,the properties in AFLOW were screened to fin the compounds that have DFT-calculated moduli (G and B),and out of the total number of compounds(3562,831),5663 compounds were found to have the G and B moduli.Here,the G and B moduli were taken as the Voigt-Reuss-Hill approximation (VRH) of bulk and shear moduli as given in the AFLOW database from Voigt (GV,BV) and Reuss (GR,BR) moduli [18],as follows:

Fig.1a shows the distribution of the moduli obtained from the AFLOW for the 5663 compounds.It can be noted that the G modulus was distributed between 0.5 and 530 GPa with a maximum distribution in the range 60–80 GPa (30%).For the B,this distribution was from 1 to 440 GPa with a maximum distribution at the range from 80 to 100 GPa(∼20%).In addition,the elemental contribution in the extracted compounds with moduli is presented in Fig.1b,and this shows that amongst 72 elements,oxygen is the most contributing element in these compounds,whereas Mg was found in 244 compounds,as highlighted in Fig.1b.The extracted compounds were also classifie based on their composition elements and crystal structure as shown in Fig.1c and d,respectively.These are mostly ternary (2931) and binary (2627) compounds,and 2550 and 1041 compounds have cubic and hexagonal crystal structures,respectively.The distributions presented in Fig.1a–d will provide models which are powerful to predict the moduli in the same range of the training set in terms of,moduli values,composition,and crystal structure.For more insight into the initial dataset,the Excel file containing the moduli (G and B),composition,and space group of the compounds to be employed in the further learning steps,is presented in the supplementary materials.

Fig.1.(a) Initial dataset containing bulk and shear mossduli collected for 5663 compounds.(b) The contribution of the chemical elements in the collected compounds used in the initial dataset.This analysis shows that the Mg contributed to 244 compounds.(c) The number of 1-,2-,and 3-element compounds in the initial dataset,showing that most of cases are ternary compounds (2931).(d) The crystal structures of the materials used in the initial dataset,showing that cubic crystal structures are the most dominant,with 2550 compounds.

The used proxy of (G/B) ratio to identify ductile or brittle behavior could in fact be used as an output to the machine learning process used in this work,but we opted not to do that due to several reasons;the firs reason is that using G/B as a targeted property will merely be a meaningless ratio in the ML model revealing little to no information about how G and B change with changing the material or crystal structure;which makes it very difficul to compare between DFT,experimental and ML results.The second reason is that G/B as a ratio does not reveal any information about the concrete value of G or B or the validity of the model in understanding those integrated values,for instance a G/B ratio of 0.5 can either be 1/2,20/40,50/100 or any ratio that results in 0.5 rendering the constructed model inefficien in giving any accurate physical or logical insight into the behavior of G and B separately or when examining their joint relationship.

2.2.Features generations and preprocessing

After preparing the initial dataset as described in the previous section,feature-related processes,including features generation and features filtering are described within this section.Firstly,considering the significanc of machine learning in properties predication and materials design,one can think about how to connect the material with the targeted property,how right can this connection be,and to what degree we can actually describe the materials? Those are powerful starting questions to build an accurate ML model that can predict the target property,and here,the “feature” is the keyword to answer the proposed questions above.Simply put,features of a specifi material are the representations of this material in order to transform it into a set of quantitative attributes which,in turn,are used as input to build the model and to predict the property in new materials.Accordingly,in ML,the type of features to be employed in the learning process is very critical,where these features should accurately describe materials,and can definitel distinguish between one material and another.In this work,crystalline materials are targeted,and accordingly,features built based on the crystal structure and composition of the compounds were chosen.These features were basically generated using the free to access Magpie software [19],in which the Voronoi tessellation structure (VTS) and the Weiger-Seitz cell representations of compounds were employed.The feature calculation in this platform is conducted through two routes.In the first the composition and the DFT-calculated parameters of the compounds including band gap,formation energy and stability for instance,along with their relaxed crystal parameters,such as lattice constants,are used to generated 271 features for each compound (presented in Table S1).Usually,these features are easily managed through the compounds information available in the open-source database mentioned previously and since they are totally based on the relaxed structure of the compound,we are to call them relaxed features here on.Attractively,these features can also be managed only through the composition of the compound and the crystal parameters of a prototype structure resembling the compound in question,those features are to be called non-relaxed features as a counterpart.By this type,the targeted property of new compounds,with no experimental history or any related DFT calculations,can be predicated,where starting from a prototype structure and by chemical substitution of the elements in the periodic table,a large number of (non-relaxed) structures are constructed,and their features are accordingly generated.In our previous works on the applications of the ML to predict the hardness[15]in crystalline materials,both the relaxed and non-relaxed features were employed,and a well matching between their predication outcomes were reported,suggesting the validity of non-relaxed features to be employed.In the present work,since the target is to classify the intermetallic compounds of Mg alloys in terms of their ductile-brittle behavior based on the G/B ratio,as predicted by ML,there will be no need to discover new compounds,and accordingly,a simultaneous dealing with relaxed and non-relaxed features is avoidable.In this regard,the relaxed set of features were generated for the extracted compounds (5663) using their DFTrelaxed crystal parameters and the counterpart calculated electronic properties (formation energy,spacegroup),as presented in the AFLOW database [12],leading to 271 features.Those are listed in Table S1 in the supplementary materials,and more information related to the features were included in our previous works [15,16].

Of course,other possible features that relate to the nature of testing conditions (loading axis and temperature) come to mind when representing a material,for example,when examining the fracture behavior of materials,the fracture is not only dependent on the structure of the material itself,but it is also dependent on the testing conditions (loading axis and temperature).In general,the moduli(elastic and shear moduli)of single crystalline materials are very sensitive to the crystallographic axis,along which the targeted material is loaded,where the variation between those parameters measured along the most docile and stiffest axes can reach to 4 folds at temperatures close to melting point.For example,experiments showed that the room-temperature shear modulus of Li single crystal along<001>is 3 times bigger as compared to that along<111>[20].This also will be significan when the temperature,at which the moduli were determined,is also considered.The experiments and calculations conducted on the single crystalline Li showed that the temperature had less effect on the moduli (bulk and shear) as compared to that of the loading conditions [6].More or less,those parameters are of a great importance when fracture behavior is investigated.Considering the main point targeted in this work,one can rise a question on how such parameters (loading condition and temperature) can be handled in the ML model.First,the initial dataset containing the compounds and their moduli (B and G) to be used in the learning process is mainly obtained from a high-throughput DFT calculations database(AFLOW).In this set,the moduli were averaged for each polycrystalline material,as obtained from AFLOW,and this is consistent with the very firs assumptions and finding reached by Pugh [6],where through the analyzing of experimental data obtained for several polycrystalline metals,it was found that metals with small G/B generally show ductile behavior.In addition,since the DFT work done in the high-throughput DFT calculations was conducted at an assumption of a static crystal or 0 K,the built ML model will be just applicable for low-temperature scale of materials,and by this model,the average outputs are predicted.

To reduce the complexity of the ML model to be built in the present work,and thusly to reduce the overall subsequent overfitting the features were subjected to a refinemen process,where unnecessary features are removed from the dataset.Here,we usually use two criterions to fin such features [21],those are variation threshold filterin (VT) and Pearson correlation (PC).In the 1st,features that have a variance less than a specifi threshold (0.01 in this work) along the cases in the dataset are considered to have no or less effect on the targeted properties (B and G) and assumed to be constant,and accordingly,they are less worthy as compared to other features with a variance that is larger than the variance threshold set.The 2nd criterion,PC,deals with the internal linear relationships between the various features,where the highly correlated features are expected to have the same effect on the targeted properties.If a strong correlation between two features is found,as it can be detected by the PC coefficien (R >0.75),then one feature can be turned aside.The VT-and PC-refinemen process resulted in 64 features for each case in the initial dataset,and those are listed in Table S2 and the PC heatmap are presented in Fig.S1 in the supplementary materials.

Up to this end and in the light of the previous conversations,one might still have two lingering concerns in mind that this discussion might alleviate,the firs is the rationale behind using the DFT data as opposed to real experimental data,and the second is why we have used the features we did in this study.To expand further upon these questions,it is pertinent to note that ML is a methodology that feeds off of data,and this data has to have the sufficien quality and quantity in mind.Yet,it is the quantity that is always favorable as it gives more room for variation and the individual data instance error contribution is negated by the sheer amount,given that the data are somewhat sensical and not pure Gaussian noise[22].The concern about DFT vs.experimental measurements is certainly justifiabl and very appropriate given the nature of the data that have been collected,DFT methodology is inherently limiting by its approximation of the wave function,and is limited even further by the approximation parameters that are involved.Yet it is a flagshi methodology that is used by many researchers in order to establish a basis of analysis to predict the intuitive behavior of materials depending on their properties.The limitations restrict themselves by firs computational time/available hardware that is related to tuning parameters (k-point mesh,cutoff energy,supercell size)and second by accuracy to experimental measurement due to modeling limitations and approximations in the theoretical foundations of the physical equations.The previous points are certainly hindering and sometimes limiting to the amount of materials that can be analyzed.Yet research after research,DFT methodology have proven that it is a good assisting tool in giving intuitive results about a specifi material especially ones that have not been experimentally examined yet [23].

The second problem about relying on experimental data rather than data collected from databases,is that experiments differ widely from one research group to another,collecting data from experimental studies done by other groups will introduce the behemothic problems of biases and external effect,without even mentioning homogeneity and cohesiveness of the large volume of collected data.To delve into the nitty gritty of those problems;experimental data are very subject to not only selective biases that would enhance the properties or performance of many materials but to general noises of measurements that are inescapable in this case [24].The solution to this problem is in fact collecting for the same material from multiple sources,which seems like a good idea in theory but in practice will severely limit the number of data that will be used for the ML process another solution is to set a number of criteria for collecting the data,which would have to be defended by a sound rationale and reviewed by the scientifi community to assess the soundness of the criteria merits.The second major problem is the problem of external effects,this includes and not limiting to;processing history,microstructure,effects of temperature and pressure and other effects as well that if we are to account for them in our ML model,we will be forced to add them as features,this will no doubt restrict the model by reducing the number of unifie data points collected from each group or create nonsensical features by imputing most of the data that miss those features.

2.3.Training and building the ML model

After the preparation of initial dataset,features generation,and fina features preprocessing,the data for training the ML models became ready to be handled further in the learning process.Generally,to an get an accurate model with balanced fitting various type of machine learning algorithms with different mathematical and statistical natures are used to train the model.In this work,we compared the performance of mainly ensemble techniques and algorithms including an XGBoost base learner and enhancing it further using boosting and bagging using two well-known algorithms;AdaBoost(XGB-Ada)and Bootstrap Aggregation (XGB-Bag),this process of ensemble learning enhances the performance of a specifi algorithm while maintaining generality and avoiding overfittin on a small-scale data as the data used in this paper becomes challenging [25].Subsequently,the data was divided into training dataset and testing dataset,80% (5096) and 20% (567),respectively,this split is called the “representative split” from here on and is used to visualize the results in Fig.2(those are presented in the supplementary file separately).The accuracy of a model is usually measured using a variety of metrics such as the Root Mean Squared Error (RMSE) and the R2score[26].RMSE follows an assumption that the error is unbiased and follows a normal distribution.It is useful when comparing the performance of several models against each other.In turn,R2is a powerful metric to judge the performance of models,individually,with no needed to other models,and this makes it more reliable as compared to RMSE in the case of a regression model that the output itself (experimental) has a considerable margin of error (due to technical parameters in DFT for example).

3.Results and discussion

Fig.2a–c present the testing results of the moduli ML models as built using XGB,XGB-Bag,and XGB-Ada,respectively,showing the ML-predicted moduli (B and G) and their counterpart DFT-calculated values.Roughly,here one can expect the quality of the built model based on the deviation of the data points from the linear guideline inserted in the figures In general,the B models from the various algorithms gave more consistent trends between ML-prediction and DFT-calculations as compared to those noticed in G models.This can be more evidently compared using the R2scores of the various ML models of the moduli,as shown in Fig.2d,where the scores of the B models are higher than that of G models using the various algorithms.Such behavior can be mainly attributed to the distribution of the moduli data used in the present work.As shown by the representative split used to train the models (Fig.2e and f).The full dataset of bulk modulus was more scattered along the full range as compared to that of the shear modulus,whereas it was mostly concentrated between 0 and 100 GPa for the shear modulus.The B data distribution allows the model to learn consistently well in a wide range of values,leading finall to a more powerful ML model.In addition,the comparison between the models built using the various algorithms employed in the present work(XGB,XGB-Bag,and XGB-Ada) reveals that the XGB-Ada based models is the most accurate with R2scores of 0.94 and 0.90 for the B and G models,respectively (Fig.2d).As introduced above,this is related to the different working nature of these algorithms,where through the application of the XGB-Ada,the sequential overtime update of the weights of models and their success or lack thereof directly affects the next model in the boosting process,this enhances the model by identifying the critical and difficul cases that might hinder the prediction accuracy in the other algorithms used.Although,this is the case in the algorithm used here,as can be seen from the accuracy score,it comes at a sacrific for the time consumed to train the data.The training and prediction times have been given in Table 1 for comparison,it can be seen that the accuracy versus complexity tradeoff comes exactly here;the sequential nature of the boosting method is more time consuming than the counterpart bagging method for the XGB base learner used in this work.That being the case,when push comes to shove,the predictive power that is provided by the adaptive boosting technique in this work is higher than its counterparts and considered paramount,and thusly any increase in accuracy is more desirable than overall time needed for the model to train or predict,given that the time is reasonably quick relative to any other methodology[27].The “stacking” of multiple ensemble models is certainly showing its effects here,although the base learner in this case is (XGBoost) the differing ensemble methods that are based on this learner show different accuracy.Fig.3 shows a simplifie inner-working fl w for the AdaBoost algorithm,harder cases,namely cases that their prediction is way off the actual prediction values are colored red.Their error is way higher than other and therefore they influenc greatly the next iteration of the ensemble through the same basic learner (XGB in this work) until the iteration completes and the ensemble reaches an acceptable accuracy.

Fig.2.(a)–(c) Testing results of the ML models (bulk and shear) built based on XGB,XGB-Bag,and XGB-Ada,respectively.(d) The R2 scores of the built models using the various algorithms (XGB,XGB-Bag,and XGB-Ada).(e) and (f) The splits (bulk and shear) used in the training and testing of the models.

Table 1 The operation time for training,prediction and the overall average accuracy given by the (R2B+R2G)/2 of each algorithm used in this work.

To show the potential of the used XGB-Ada model for predictions,the built model was used to predict the moduli for crystalline materials,and for this purpose,the crystal information of over 30k compounds available in the Inorganic Crystal Structure Database (ICSD) were extracted,where those compounds were not seen by the models before.The information,including crystal parameters and electronic properties,was used to generate the features,which,in turn,are the inputs to predict the moduli of the counterpart compounds.This mass prediction process can be also utilized to fin the moduli of compounds listed in other open data sources,like OQMD which contains the information of more than 1 million compounds.The mass predication results are shown in Fig.4a and b,where the shear and bulk moduli of the ∼30k ICSD compounds were presented together with their formation energy.In addition,the ML-predicted shear and bulk moduli were presented in Fig.4c.Unsurprisingly,as shown by the data distribution in Fig.4c and inserted marginal histograms of the two moduli,the predicted data has a similar distribution with that of the initial data (B and G) used in the learning process.

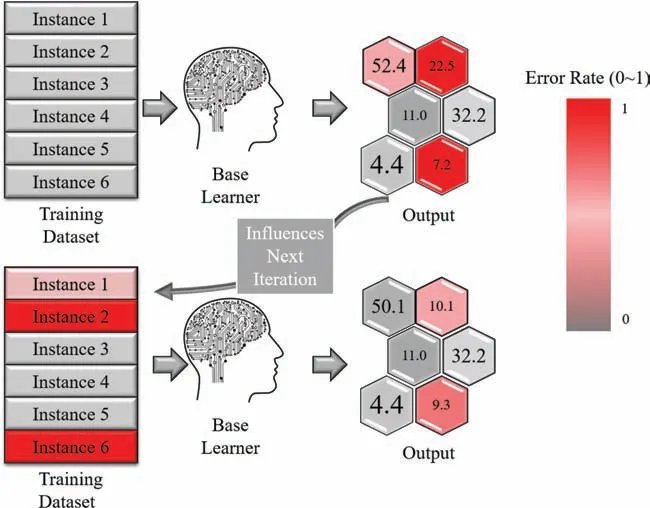
Fig.3.Simplifie inner-working fl w of the AdaBoost algorithm.The series nature of this algorithm can be seen,where each iteration heavily influenc s the other based on the difficul cases.

Fig.4.(a)–(c) Large-scale prediction of the bulk and shear moduli of compounds presented in ICDS (∼30k) using the ML models built using the XGB-Ada algorithm.(d) The ML-predicted moduli (shear and bulk) of the Mg-containing compounds,as listed in the ICDS (1101).(e) and (f) The validation results of the ML models built in the present work,showing the ML-predicated moduli and their counterpart DFT-calculated moduli of 21 Mg-containing compounds.(g) The bulk modulus as function to the G/B ratio of the 1101 compounds listed in ICDS,as predicted by the ML models.

By a screening process,the moduli of the Mg-contained compounds (1101) were extracted from the mass-predicted data in Fig.4a and b (Fig.4d),For validation of the ML models,the moduli of 5 compounds(Mg2Ca,MgCd3,MgCu2,Mg2Ge,and Mg2Sn) were extracted from experimental [28–32] and DFT sources [33] for direct comparison between the constructed ML model and obtained results from literature and is shown in Table 2.A well matching can be seen between the ML and experimental values collected for those compounds with an average 4.92% and 16.9% errors for both the bulk and shear modulus respectively as opposed to 7.19 and 13.8% average errors for B and G of the DFT method done by Ganeshan et al.[33].For further confirmatio between DFT and ML done in this work,21 Mg-containing compounds were chosen to conduct further confirmin DFT calculations,and those were not included in the initial dataset and nether have any DFT-based elastic properties calculations.The selected compounds are listed in Table.3 along with theircrystal information and the prediction interval of the model,in short,the prediction interval gives us a glimpse on the interval at which the prediction of the ML model will yield 95%of the time.This is to ensure that our model is a statistical methodology that is open for interpretation and optimization,for more information please refer to the supplementary document.The Ab-initio calculations done in this work have been carried out by utilizing the Perdew-Burke-Ernzerhof (PBE) exchange correlation functional and generalized gradient approximation(GGA) provided by the quantum espresso (QE) DFT calculation package [34].To calculate the elastic constant tensor needed for bulk and shear moduli calculations,Thermo_PW driver extension implemented for Quantum Espresso (QE)was used [35] with a consistent 1×1×2 supercell for each calculated compound and a dense 6×6×6 k-point mesh was used for the supercells with an optimized cutoff energy of 60 Ry and a fin self-consistency convergence threshold of 10−10Ry to ensure a smooth transition to convergence for the energy calculation.As for the accuracy of the 6×6×6 k-point mesh usage for each of the 21 compounds,an additional convergence plot (Fig.S2) for each (k-point vs.energy difference [eV]) has been given in the supplementary materials.Here we prioritize two things based on the convergence plot;accuracy and cost efficien y,in other words,we opted to use a mesh that shows early convergence while it being computationally feasible,i.e.(6×6×6).From Fig.S2 for each of the 21 compounds,it can be noted that most of the compounds had shown a convergence behavior beginning at 6×6×6 mesh.Therefore,this mesh can be used for each compound in order to calculate their elastic constants.Another reason why a reasonable 6×6×6 mesh can be used in the current DFT calculations,is to emulate the high throughput calculations that are generally done for G and B moduli,and using a higher mesh for those calculations could institute a computational encumbrance that is not viable to establish for the 21 compounds in this work,which aligns with this work that is intended to give a large scale prediction to give an insight on the applicability of our model rather than give a detailed DFT case study.

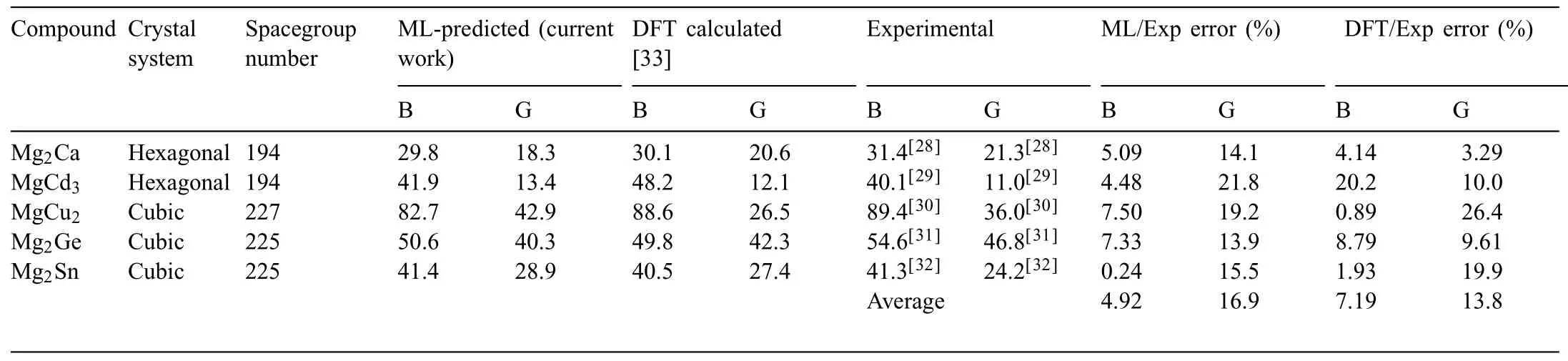
Table 2 The compounds selected to validate the ML models built in the present work using the experimental calculations [28–32] and DFT calculations done by Ganeshan et al.[33].

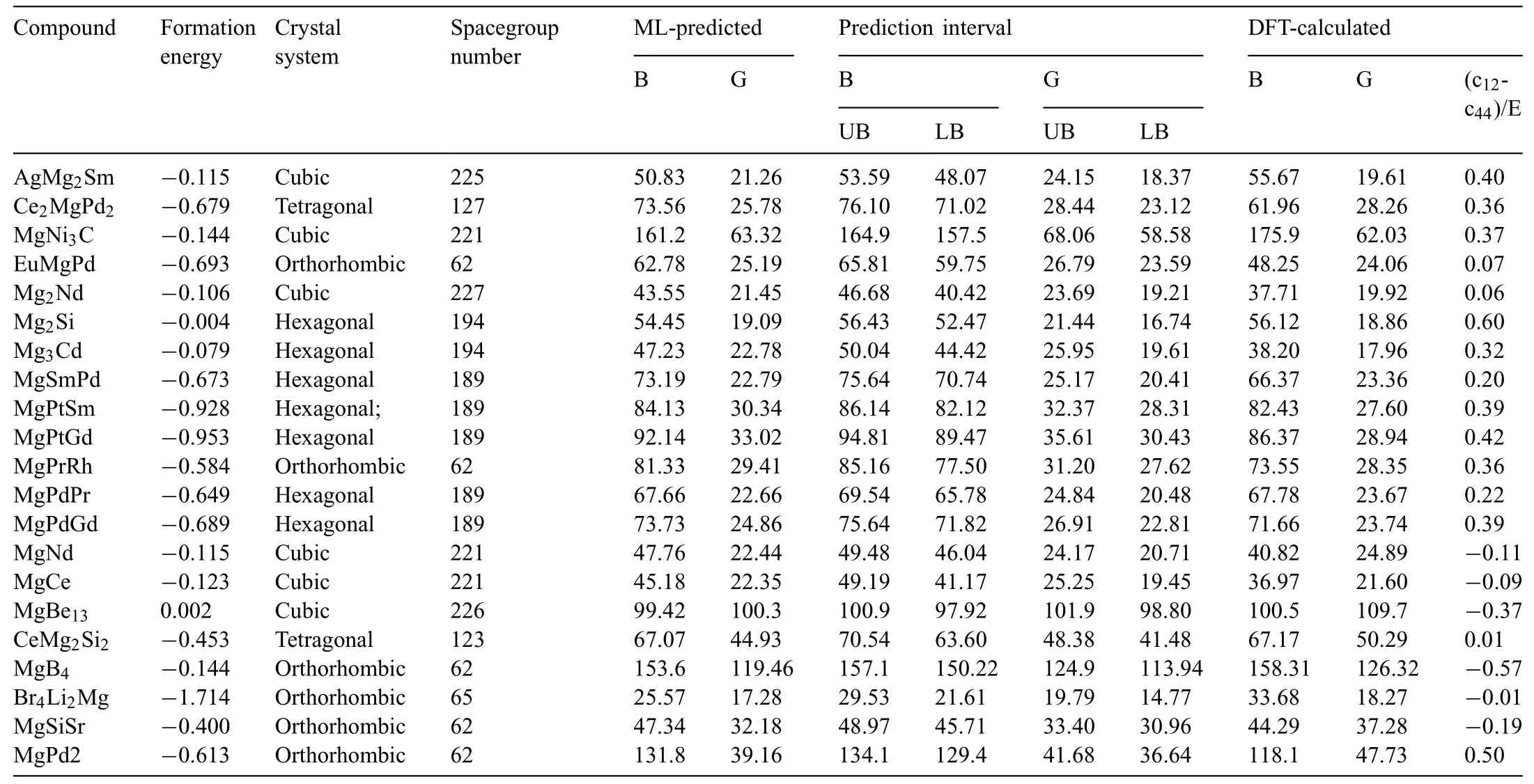
Table 3 The compounds selected to validate the ML models built in the present work using the DFT calculations.The unit of G,B and E is GPa,and for the formation energy is eV/atom.The Upper Bounds (UB) and the Lower Bounds (LB) of the prediction interval are given alongside each modulus.

The DFT validation results using the selected compounds are shown in Fig.4e and f,and additionally,they were listed in Table 3.It can be seen from Fig.4e that the ML-predicated moduli of the addressed compounds and their counterparts calculated using the DFT,were fairly matched with each other.The R2scores,for both the bulk(0.96)and shear(0.98)moduli,as reached through the validation process,were even higher than those in the testing results (Fig.2c).This can be attributed to both the characteristic of the initial dataset used in the learning process and the selected compounds.Here,most of the addressed compounds (Table 3) were found to have moduli in the low range (less than 100 GPa(Fig.4e and f)),in where the moduli in the initial dataset are mostly distributed,especially the case of shear modulus(Fig.1a).

Here,as an additional step,some experimental results to confir the ML prediction are presented.For this purpose,experimental works on the Mg17Al12compound,as reported by other groups [36,37] were presented and compared with the ML results in the present work.It can be seen from Fig.4g that the ML-predicted G/B ratio of this compound was 0.52,which is within the range of ductile materials,but close to that of brittle materials,and this behavior can be related to the chemical bonding nature of the Mg17Al12.In this regard,the firs principle calculations of the charge density conducted for this compound revealed that the Al-Al and Mg-Mg bonds were covalent and metallic,respectively [38].This type of bonding in the Mg17Al12,where the covalent and metallic bonds are mostly comparable to each other,brings it to be located close to the critical point where the ductile-tobrittle transition occurs.On the other hand,the experimental works on mechanical properties of Mg alloys containing the Mg17Al12phase revealed that this phase exhibited a brittle fracture at room temperature,which is inconsistent with the related ML results of the Mg17Al12,as found in the present work.The contrary between the experimental results and ML finding here can be attributed to that the Mg17Al12compound in real experiments is usually defected,whereas ML model were mainly built based on the perfect crystal features,as described in the“Features generations and preprocessing”section.Most works including this phase showed that the Mg vacancies and AlMg(Al-substituted Mg) are easily created in the Mg17Al12,leading to the formation of Al-rich compositions.In this composition,the number of metallic bonds(Mg-Mg),which explained the ductile behavior predicted for this compound,is reduced,and as a result,the brittle behavior becomes more dominated experimentally.In addition,based on the Pugh’s assumption in his criterion,the work hardening needs to be neglected,and accordingly,this criterion will be more suitable to assess the behavior in defect-free structures.Up to here,all microstructural factor,such as dislocation density,grain size,and texture,can lead to adverse behaviors compared to that predicted by the ML model where it is chiefl built using perfect crystal assumptions.

The validation of the predictive ML model built in the present work is the starting point where more material science concepts related to the targeted behavior (ductile-brittle)are to be introduced for the further discussions.First,considering crystalline materials,the ductile-brittle behavior is intrinsically related to the type of chemical bonds which form in the unit cell of these materials.Usually,the brittle behavior is conjugated with the covalent bonds between atoms,like diamond,where these bonds are directional and very strong,making the covalent-bonded materials brittle and hard to be deformed plastically.In addition,due to the strong interaction in ionic bonds and the large Burgers vector,ionic crystals,like NaCl,exhibit brittle behaviors.On the other hand,metallic materials are generally ductile,due to the weak and non-directional metallic bonding between the atoms.Based on this simple concept,the DB characteristics of materials that have variety of bonding systems (heterogenous bonds) are mainly associated with contribution of each type of bonding.The more contribution of metallic bonding leads to a more pronounced ductile characteristic,and more brittle characteristics will be notable for the covalent-and/or ionic-dominant materials.Fig.4g shows the G/B ratio of the 21 Mg compounds,as predicted by the ML model built in this work,and the ratio predicted to the gold (Au),the well-known highly ductile metal.As shown by the Fig.4g,the ratio of Au was predicted to be 0.22,indicting its ductile characteristic.In addition,the ratio of Mg17Al12,one of the most common intermetallic compounds that form in AZ series (AZ31,AZ61,and AZ91),was predicted and is highlighted in Fig.4g.The ML-predicted ratio of this compound was found to be 0.52,indicating its ductile nature.This is consistent with the find ings of Wang et al.[39],who investigated the DB characteristic of Mg17Al12based on the G/B ratio determined using their DFT calculations ((G/B)DFT=0.52).Their work was mainly designed to investigate how the DFT parameters,such as kpoints,cutoff energy(Ecut)and DFT method,can influenc the calculation output (G/B ratio).They found that k-point mesh is the most effective parameter during the DFT-based elastic calculations,where it was reported that the elastic moduli changed pronouncedly when k-point is tuned,and this change was more significan as compared to those associated with the tuning of other parameters.6×6×6 k-point was determined to be the optimum mesh for the calculation,and no further change was recorded by using denser meshes,like 8×8×8 or 10×10×10.

Pettifor criterion is another method employed to trace the DB behavior in crystalline materials.Using this method,crystals with non-directional bonds (metallic materials) exhibit a positive Cauchy pressure (c12-c44),indicating a ductile behavior,whereas covalent crystals in which bonding is directional,the pressure is negative,and thus,they show brittle behavior[40].Recently,a correlation between the two criterions (Pettifor and Pugh) was established using the elastic modulusnormalized Cauchy pressure ((c12-c44)/E),and this monotonic correlation was found to be valid for cubic materials [41].In the present work,the DB ratios of both cubic and non-cubic Mg-based compounds,as predicted by the ML models,were represented by their counterpart DFT-calculated ((c12-c44)/E)values.The results shown in Fig.5a,accordingly,can confir further the validity of the present ML models used to predict the GB ratio.The DB behaviors predicted by the ML models based on the Pugh criterion (G/B ratio) was fully consistent with the behaviors of the same compounds as found by DFT calculation based on Pettiford criterion (Cauchy pressure).

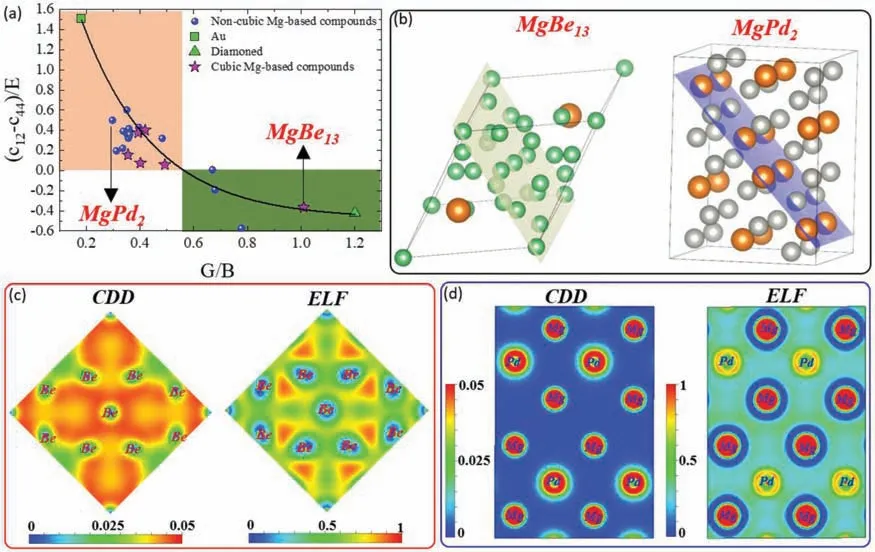
Fig.5.(a) DFT-normalized Cauchy pressure ((c12-c44)/E) of the 21 compounds used in the validation process as function to their G/B ratios predicated by the present ML models,the red-highlighted and green highlighted area shows the ductile and brittle ranges,respectively.The Au and diamond were also included in this figur to adjust the range from max-ductility (Au) and max-brittleness (diamond).In addition,the star symbols show the Mg-containing compounds with cubic crystal structures.(b) The crystal structure of two compounds (MgBe13 and MgPd2) chosen from the 21 compounds to conduct the calculations of charge density distribution (CDD) and electron localization function (ELF).The highlighted crystallography planes in this figur are planes where the calculations were conducted.(c) and (d) The CDD and ELF calculations of the MgBe13 and MgPd2,respectively.

For more interpretations on the DB characteristics,chemical bonding should be addressed,and here,two compounds(MgBe13and MgPd2) were chosen to conduct charge density distribution (CDD) and electron localization function (ELF)calculations.Those compounds were taken from the two different ranges,ductile and brittle,as shown by Fig.5a.Figures 5(b-d) show the structures,CDD,and ELF of MgBe13and MgPd2,respectively.The CDD map of the MgBe13taken in the highlighted plane (Fig.5b) showed a strong interaction between the Be atoms in this plane.For more detail on the nature of these interactions,the ELF calculated in the same plane is presented in Fig.5b.ELF represents how electron clouds are localized in a specifi crystallographic plane,indicating the type of the bonding.For covalent bonds,electrons are highly localized with ELF values of higher than 0.5.On the other hand,the electrons are distributed more homogenously in metallic bonds,and this is indicated by an ELF value of 0.5.Based on the ELF concept,one can see a strong electron localization,with ELF=0.75,between Be atoms,suggesting a strong covalent bonding between them in this plane.This can explain the brittle behavior of MgBe13,as found through the ML-predicted G/B ratio of this compound(1.009).In comparison,the ductile behavior of the MgPd2compounds predicted by the ML models (G/B=0.3) is attributed to the metallic bonding between the atoms in the highlighted plane (Fig.5b).As shown by the ELF map of the plane in MgPd2compound,the less electron localization was noted with ELF ∼0.5,confirmin the dominance of metallic bonding in this compound.Based on the present electron localization and charge density analyses of the chosen compounds (MgBe13and MgPd2),one can clearly observe the potential of the ML models to predict the elastic properties,where the predicted properties are quite consistent with the bonding nature of these compounds,as found by the ELF.

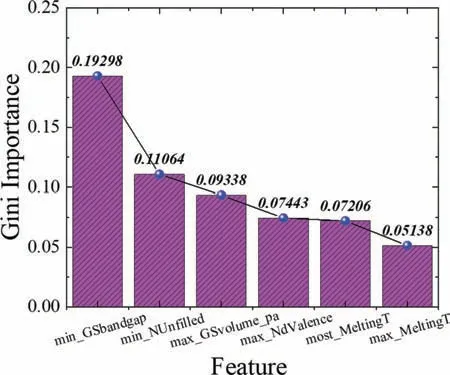
Fig.6.The average feature importance that have been obtained for both ML models of G and B.

To show how the ML model can also provide similar physical intuition for interpretability,Fig.6 shows the top 6 important features based on Gini importance [42] that can significantl influenc the output (moduli),as predicted by the ML model built in this work.It can be seen from Fig.S2 that a band gap-related feature (min_GSbandgap : minimum ground-state bandgap of an element in a specifi composition)is the most influentia one with an average Gini importance of 0.193.Interestingly,from a material science point of view,the band gap is a very important parameter that can affect the strength of materials.In this regard,the band gap in crystalline materials is highly correlated to the dislocation mobility,where it was found that the energy needed for breaking down bonds constraining the dislocations during the plasticity process is directly proportional with that needed for exciting two electrons through the band gap,thus,the wider gaps is usually conjugated with high strength in materials.Based on the main assumptions made by Pugh in relation between the ductile/brittle behavior of materials with their moduli,the yield strength (σy),which describes the plasticity of materials,was scaled with the shear modulus of the counterpart material.Furthermore,the fracture stress(σF)was scaled with the bulk modulus,finall leading to the criterion of Pugh as follows:

Based on this equation and according to the aforementioned discussion,it is worth mentioning that the moduli in general can be highly scaled by the bandgap-related feature(min_GSbandgap),which is consistent the ML model giving it an interpretative edge.

Up to here,the validity of the built ML models has been supported by the testing results (Fig.2d),DFT calculations of the moduli in some compounds (Fig.4 e and f and Table.3),and more deeply,by the CDD and ELF calculations.Accordingly,the present model can be employed to foresee the DB behavior of intermetallic compounds that form in Mg alloys.To achieve that,the crystal information of these compounds in various series of Mg alloys,such AZ,WE,and ZX,were collected from OQMD.The information was then used to generate features,which in turn,are the inputs to predict the moduli of these compounds.Each of these compounds were chosen based on its formation energy,where it has the lowest formation energy as compared to other competing phases with the same composition.The prediction results of the targeted Mg alloys series are presented in the ternary contours in Fig.7 as well.

In general,along with the volume fraction,distribution,morphology,and size of the IMCs that form in metallic alloys,the DB characteristics of these compounds play an axial role to determine the mechanical performance and corrosion response of the alloy.For example,the brittle and strong IMCs can enhance the strength of steel based-materials (hardening by the 2nd phase),but this usually comes at the expense of its plasticity [43].To reduce the harmful effect of IMCs compounds on the plasticity,and to reach a simultaneous enhancement of strength and ductility,other parameters (volume fraction,distribution,morphology,and size) are usually optimized [44].On the other hand,controlling those parameters influenc differently in Mg alloys as compared to other metallic materials.This can be explained based on the type of slip systems which are activated in Mg during the plastic deformation,where generally,dislocations in Mg alloys belong to one of three families,those are basal family (3 systems) with low critical resolved shear stress (CRSS),prismatic (high CRSS),or pyramidal (high CRSS).Based on their CRSSs,the basal slip is activated first and due to the limited number of slip systems in this family (von Mises yield criterion),pure Mg exhibits brittle behavior.To enhance the ductility and accommodate the plastic strain in the pure Mg,more contributions from prismatic and pyramidal families with high CRSSs is needed.Intrinsically,this can be achieved by alloying Mg with some other elements,like Y,which can alter the deformation mechanism,leading to enhanced plasticity in this alloy(Mg-Y).One convincing interpretation of this enhancement is that substitution of Y by Mg in the alloy was found to reduce the firs intrinsic stacking fault energy of pure Mg.Since the partial dislocations of those faults have pyramidal characteristics,and thus,by reducing their stacking energy,these faults will act as heterogeneous source of pyramidal dislocations,leading to enhance plasticity [45].Another path to get the plasticity enhanced is by controlling the IMCs characteristics.In this regard,it was found that the hardening by the 2nd phase particles can also enhance the plasticity[46].This was explained based on the role of the particles to increase the strength in the basal plane,and this results in reducing the ratio between CRSS of prismatic slip to that of basal slip [47],leading finall to enhance the plasticity by more contribution of non-basal (prismatic) dislocations.Going back to the ML-evaluated BD characteristics of the three series (Fig.7),one can see that the ZX (Mg-Zn-Ca)and WE (Mg-Y-Ce) series show vaster areas in the contour maps with brittle characteristics as compared to that in AZ series.On the other hand,in the AZ series,the area with ductile characteristic is more dominant as compared to the brittle one.Considering the effect of the brittle and strong IMCs on the strength and plasticity in Mg alloys together with the ML-evaluated DB characteristics done in this work,it can be stated that results reached here might generally explain more promising performance which commonly noticed in such alloys (ZX and WE).All in all,in addition to facilitate the calculations related to the elastic moduli of crystalline materials,the present analyses provide an additional tool to figur out the performance-properties-structure relationships in Mg based-alloys.Yet,we as a material science community should proceed with cautious optimism about ML,although it is indeed a discernable tool for researcher to make swift predictions about behaviors or properties of materials based on previous experiences,the keyword here is “reliability”,and this pertains to the dataset,model and validation procedure.For the dataset;one must follow the 7Vs of big data [48],for the model one must appropriately choose a model that is complex to the point of interpretability and generality without overfitting ML can be very alluring with its glamor of rapid predictions,and it certainly is as we have shown in this work,yet one should always remember the infamous quote of“garbage in garbage out” when talking about ML,everything before the learning process should have the necessary quality to be meaningfully interpreted and predicted.

Fig.7.The ML-predicted G/B ratios of intermetallic compounds that form in Mg alloys,including AZ,ZX and WE series.These compounds were selected based on their formation energy,where they have the lowest energy as compared to other competing phases for the same composition.

4.Conclusions

The present work was conducted to build machine learning (ML) based models that can be employed to accelerate the calculations of elastic moduli (B and G) in crystalline materials,and to evaluate the DB (ductile-brittle) behavior of such materials based in Pugh criterion (G/B ratio).The results reached and reported in our work showed that ML is a powerful technique,and by which,accurate models to predict the moduli were built using an ensemble learning algorithm (XGB-Ada),where the R2scores of 0.94 and 0.92 were reached for the B and G models,respectively.The validity of the built models done by DFT calculations for some compounds showed a well consistency between the DFTcalculated and ML-predicated moduli.In addition,the DB behaviors evaluated by ML-predicated moduli of MgB13 and MgPd2 agreed with the type of chemical bonding in these compounds,as found by the DFT calculations of CDD and ELF.According to the DFT validation results,the models was used further to predict and screen large number of compounds ∼30k.Beside the acceleration of calculations related to the elastic moduli of crystalline materials,the present analyses provide an additional tool to figur out the performancestructure relationships in Mg based-alloys,where prediction and screening were conducted on intermetallic compounds that might form in three Mg alloys series.

Funding information

This research was supported by National Research Foundation (NRF) of South Korea (2020R1A2C1004720).

Data availability

All data including tabular,code,structural information or else can be obtained either through the attached file or through the designated GitHub page for this work:https://github.com/russlanj/Ductile-Brittle-Mg-Alloys-Data and https://kotibahamad995.wixsite.com/aem-skku/machinelearning-codes the data is also available upon request from the authors.

Declaration of Competing InterestNone.

Supplementary materials

Supplementary material associated with this article can be found,in the online version,at doi:10.1016/j.jma.2022.05.006.