基于纳米压痕的煤系泥岩细观力学及断裂性能试验研究

2023-03-24顾士坦逯英棋李文帅蒋邦友肖华建

煤炭工程 2023年2期

顾士坦，逯英棋，李文帅，蒋邦友，肖华建

(1.山东科技大学能源与矿业工程学院，山东青岛 266590；2.山东科技大学土木工程与建筑学院，山东青岛 266590；3.天地(常州)自动化有限公司，江苏常州 213000)

在我国已探明的煤炭储量中，有60%埋深在800m以上，53%埋深大于1000m[1]，巷道围岩稳定性控制对深部煤炭资源开采至关重要[2]。煤矿深部巷道大多沿沉积岩层掘进，例如煤系泥岩，研究煤系泥岩的力学性质对于控制巷道围岩稳定性具有重要意义。近年来，众多学者对煤系岩石的宏观力学性质开展了大量的研究，包括岩石的强度、变形以及破坏特征等。然而，由于岩石的非均质性，岩石宏观的破裂多是源于其内部微观裂纹的起裂、聚集和扩展[3]。因此，有必要从微观尺度研究煤系泥岩的力学行为和断裂特征。

纳米压痕试验是一种基于弹性接触力学理论，利用金刚石压头测量材料在压入过程中的载荷-压入深度关系曲线，来获得压痕点区域材料的细观力学参数的一种方法[4]。Constantinides等[5]利用压痕点阵测试和统计分析的方法，提取了不同相的细观力学性质。利用该方法，许多学者围绕煤和页岩[6，7]等材料开展了大量的纳米压痕试验，获得用于评估其力学性质的细观弹性力学参数。根据线弹性断裂力学理论，通过测量压痕表面裂缝长度即可得到该压痕点区域材料的断裂韧度[8]。然而，泥岩属于典型的多相准脆性材料，在压入过程中很难获得表面放射性裂纹[9]，无法直接观测到压痕裂纹及其几何尺寸。因此，部分学者基于能量守恒原理，利用压入过程中总能量与弹性能、塑性能及断裂能之间的关系，研究了材料的细观断裂性能[10，11]。然而，目前很少有涉及煤系泥岩的研究。由于煤系泥岩的非均质性，获得泥岩各相的细观力学性质及断裂参数对于理解其宏观破坏行为具有重要的意义。

鉴于此，以阜阳口孜东煤矿煤系泥岩为研究对象，对其开展了纳米压痕试验，基于Oliver-Pharr方法及能量原理，研究了泥岩岩样的细观力学性质及断裂力学特征，探讨了泥岩内部不同矿物成分之间的细观力学行为差异，对于进一步理解煤系泥岩破坏行为具有重要的意义。

1 纳米压痕试验原理

1.1 弹性模量和硬度

纳米压痕试验是通过使设备压头尖端与试样表面接触，然后连续施加压痕载荷，并记录压痕深度或位移随压痕载荷变化的一种方法。典型的纳米压痕试验获得的载荷-位移曲线如图1所示，图1中，Pmax为峰值载荷，hmax为最大压痕深度，hf为弹性卸载后的最终压痕深度。根据该卸载曲线，可以计算该压痕点的细观力学性质[12]。

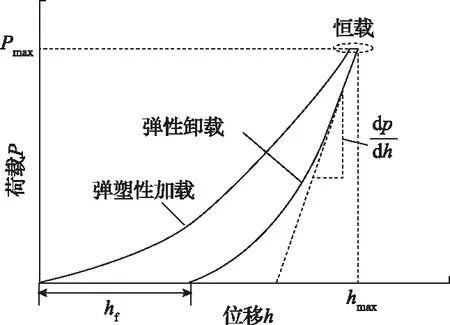
图1 典型的纳米压痕试验载荷-位移曲线

由图1可知，初始卸载刚度可以表示为[4]：

式中，P为压痕载荷。

初始卸载曲线可以通过幂律函数进行拟合[4]：

式中，Ac为峰值载荷时刻压头与试样的接触面积；Er为约化弹性模量。

对于本次试验中采用的Berkovich压头(中心线与侧面夹角θ为65.35°的正三棱锥)，接触面积Ac可以表示为：

图1中，hc为压头与试样的接触深度，h为压痕深度，其中，接触深度hc可以通过下式确定：

式中，Pmax为峰值载荷，ξ=0.75。通过式(1)—(4)，即可计算得到Er。

约化弹性模量Er与试样和压头的弹性模量和泊松比密切相关，可以通过下式确定：

式中，E和v分别代表试样的弹性模量和泊松比；Ei和vi分别代表压头的弹性模量和泊松比。对于本试验中使用的压头而言，Ei和vi分别为1140GPa和0.07。压痕点的弹性模量可以表示为：

硬度H可以表示为：

1.2 断裂韧度

在泥岩压入过程中，往往较难观测到放射性裂纹，无法准确地测量裂纹长度。鉴于此，本文通过能量法计算断裂韧度。基于经典线弹性断裂力学理论，材料的断裂韧度可以表示为[13]：

式中，Gc为裂缝扩展单位面积所消耗的能量，可以表示为：

式中，Wfrac为断裂能，Afrac为开裂面积，近似为最大压入深度时的接触面积Ac[10，14]。

在不考虑热耗散的情况下，压痕过程中产生的总能量Wt可以分解成弹性能We和不可逆能量Wir。而不可逆能量又由塑性能Wp和断裂能Wf组成，如图2所示。则断裂能可以表示为：

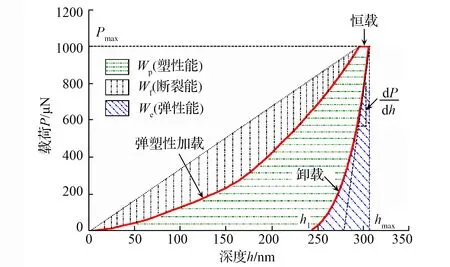
图2 能量分解示意

Wf=Wt-We-Wp

(10)

对于纳米压痕试验，其加卸载曲线可以通过幂律函数进行拟合[4]：

式中，K，n，α和m均为拟合得到的参数。通过对式(11)进行积分，即可得到Wt和We。

塑性能Wp与Wt存在以下关系[9，15]：

通过式(10)计算得到断裂能Wfrac，从而进一步获得压痕点的断裂韧度。

1.3 统计分析

以纳米压痕试验获得的细观力学参数为基础，通过统计分析的方法来评估泥岩岩样各相的细观力学性能。假定各相力学性质服从Gaussian分布，可以通过多峰曲线对试验结果进行拟合[5，16]：

式中，μ和σ分别代表各拟合峰值的平均值和标准差。

2 岩样制备和试验方法

2.1 岩样制备

泥岩样本取自安徽省阜阳市口孜东煤矿，泥岩呈灰色，含水率约为2.4%。根据XRD结果，泥岩的主要矿物成分为石英(7.4%)、绿泥石(43.1%)、高岭石(12.3%)以及伊利石(37.2%)等。

由于纳米压痕试验对岩样表面光滑程度要求较高，在试验之前，首先要对岩样表面进行光滑处理(精磨和抛光)：在获得初始研磨后的泥岩岩样后，将岩样浇筑于环氧树脂中，以便为后续的精磨和抛光创造整体稳定性条件；采用52μm、35μm、22μm和15μm等级的碳化硅纸对岩样进行研磨；进一步利用9μm、6μm、3μm、1μm和0.05μm等级的金刚石悬浮液进行精磨，并在抛光布上进行抛光[17]，即可得到用于纳米压痕试验的泥岩岩样。

2.2 试验方案

利用Hysitron T1 Premier纳米压痕测试系统，针对光滑处理后的泥岩岩样开展了一系列纳米压痕试验。本研究随机选取了两个50μm×50μm大小的代表性区域开展纳米压痕试验，如图3所示。在该区域中，纵横向的压痕点间距均为10μm，每个测试区域均包含25个压痕点(图3)，总计50个压痕点。测试时，采用力控制加载模式，以200μN/s的恒定加载速度，加载至1.0mN；然后在最大载荷处稳定2s以消除蠕变效应[18]；之后，按照加载时的速度卸载至0μN。

图3 岩样表面待测试区域

3 细观力学与断裂性能

3.1 载荷-位移关系

其中一个测试区域的典型泥岩纳米压痕载荷-位移关系曲线如图4所示。可以看出，在相同的最大压痕载荷条件下，压痕点的压痕深度变化范围约为50～600nm。图4中，最左侧的曲线压痕深度要明显低于其他曲线，表明了该压痕点区域对外部作用力有较强的抵抗作用，可能反映了泥岩中硬质矿物的力学性质(石英等)；最右侧的部分压痕深度最深的曲线，可能代表了岩样表面最薄弱区域或软弱矿物的力学响应(孔隙或软弱的黏土矿物等)。

图4 典型的泥岩纳米压痕载荷-位移关系曲线

3.2 细观力学性质

根据纳米压痕试验获得的载荷-位移关系曲线，可计算得到每个压痕点区域的弹性模量和硬度，其中两个测试区域的弹性模量和硬度分布如图5和图6所示。两个测试区域中的弹性模量和硬度云图颜色差异较大，表明了细观尺度上泥岩岩样的非均质性。

图5 测试区域1的弹性模量和硬度分布

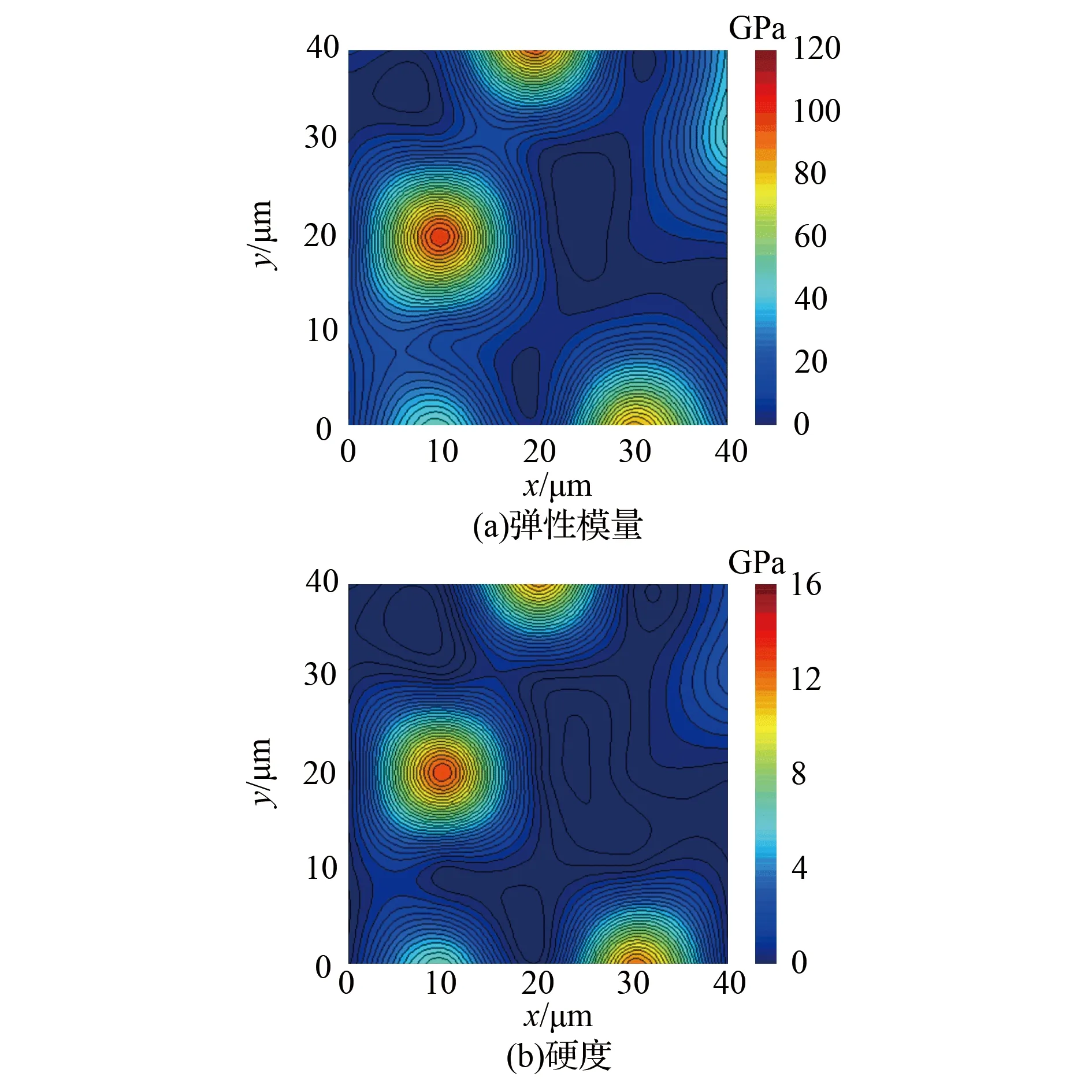
图6 测试区域2的弹性模量和硬度分布

弹性模量分布如图7所示。由图7可知，泥岩岩样的弹性模量变化范围较大，最低约为2.0GPa，最高达到114GPa；此外，柱状图中存在不止一个频率峰值。

图7 弹性模量分布

在0～4GPa区间(占比4.0%)，岩样的弹性模量较小，该区域压痕点可能存在孔隙或极软弱矿物成分。随着弹性模量的增加(4～14GPa范围内)，频率也逐渐增加，且该区间占比达到48.0%。根据XRD结果可知，该区域弹性模量所代表的的矿物成分可能为黏土矿物(包括伊利石和高岭石)，以及部分黏土矿物-绿泥石混层(压痕点位置可能处于两种矿物之间)。当弹性模量从14GPa增加到62GPa时(其中，14～32GPa之间占比约为20.0%)，该区间的占比约为30.0%。结合XRD分析结果，该区间弹性模量代表的矿物可能是绿泥石，以及绿泥石与坚硬矿物(例如，石英等)混层。随着弹性模量的增加，分布在84～114GPa区域内的弹性模量占比约为18.0%，该范围内弹性模量较高，代表了石英矿物的力学特征。根据各压痕点测得的弹性模量，可以计算得到各相弹性模量均值为31.9GPa，远高于泥岩宏观弹性模量[1]。泥岩各相之间的纳米压痕数据(弹性模量、硬度或断裂韧度等)存在较大的差异，各细观力学平均值结果可能无法反映其真实性质。

利用Gaussian分布函数，对弹性模量进行多峰拟合，如图8所示。弹性模量概率密度曲线表现为三个明显的峰值。结合XRD结果，从该曲线中可以近似获得三种不同的矿物：黏土矿物，或黏土-绿泥石混层；绿泥石，或绿泥石-石英混层；石英。

图8 弹性模量概率分布

各相的弹性模量参数见表1。表1中，黏土矿物的弹性模量约为7.83GPa，这与以往的研究略有不同。对于黏土矿物，Zhang等[19]测得的黏土矿物弹性模量小于5.0GPa，而Liu等[12]测得的结果约为22.3GPa，两者相差较大。作者分析认为，黏土矿物弹性模量的差异很可能与试样的含水率有关。对于石英而言，本研究中测得的其弹性模量约为97.3GPa，该数值与Zhu等[16]获得的石英相的弹性模量较为接近(～104.2GPa)，但略低于Broz等[8]针对纯石英相获得的试验结果(～117.6GPa)。

表1 煤系泥岩各矿物成分弹性模量

3.3 断裂韧度

根据能量原理，进一步计算得到了泥岩表面压痕点区域的断裂韧度。需要指出的是，由于本试验中部分加载曲线出现了“跳跃”现象(图4)，无法通过幂函数进行拟合。因此，试验中获得了29组有效断裂韧度数据，如图9所示。

图9 断裂韧度分布

从图9中可以看出，在0～0.2MPa·m1/2范围内，频率约为48.3%，反映了泥岩表面大多数矿物成分(主要为黏土矿物)的断裂韧度。当断裂韧度从0.2MPa·m1/2增加到0.4MPa·m1/2时，该区间频率约为20.7%；随着断裂韧度的进一步增加，0.7～1.1MPa·m1/2范围内的占比约为10.3%。结合弹性模量分布(图7)，0.2～1.1MPa·m1/2范围内(总占比约为40.0%)的断裂韧度所代表的矿物成分可能为绿泥石，以及绿泥石与石英混层。当断裂韧度增加到1.6～2.3MPa·m1/2范围内时(占比约为20.7%)，该区域表现为较高的断裂韧度，反映了石英矿物的力学响应。

断裂韧度概率分布如图10所示，泥岩各主要矿物成分的断裂韧度参数见表2。由图10可知，弹性模量和断裂韧度的概率密度曲线呈现相似规律。

图10 断裂韧度概率分布

由表2可知，所有压痕点中黏土矿物的断裂韧度所占比例高达70.0%，表明黏土矿物成分对于泥岩宏观断裂力学性质起决定性的作用。对于黏土类矿物，其断裂韧度约为0.09MPa·m1/2，抵抗裂纹扩展的能力较差；而对于绿泥石类矿物和石英矿物，其断裂韧度分别为0.91和1.95MPa·m1/2，表现为较高的断裂韧度。Broz等[8]对纯石英相的断裂韧度进行了测试，其得到的石英的断裂韧度约为1.6MPa·m1/2，与本文的研究较为接近。