基于GMM-DBC 的CSI 室内定位算法

李新春，李莹

(1.辽宁工程技术大学 电子信息工程学院,辽宁 葫芦岛 125105；2.辽宁工程技术大学 研究生院,辽宁 葫芦岛 125105)

0 引言

随着时代的进步和科学的发展，定位技术在定位精度、可靠性方面有了实质性的突破.定位分为室外定位和室内定位.室外定位技术如GPS、基站等已经可以满足在室外场景下的定位需求.然而，受障碍物遮挡、多径效应等因素的干扰，GPS 等技术不能满足室内定位的需求，所以室内定位方法成为近年来研究的热点[1].室内定位从技术角度可以采用Wi-Fi、蓝牙、蜂窝网络、超宽带(UWB)、超声波、雷达、地磁指纹等，实现室内人员导航和对室内人、物的定位及跟踪[2].其中由于Wi-Fi 设备在现实生活中设备成本很低且普及度很高[3]，所以本文选用Wi-Fi 进行室内定位的研究.

传统的Wi-Fi 室内定位方法多采用由多条路径信号强度叠加而成的接收信号强度(RSS)进行定位.但室内环境的复杂性和多径效应会使RSS 波动较大，不够稳定[4].为了克服RSS 的缺点，出现了利用更稳定的信道状态信息(CSI)代替RSS 进行室内定位的方法.CSI 室内定位方法分为确定性方法和非确定性方法.确定性方法有K 均值算法(K-Means)、K-近邻算法(KNN)以及改进的KNN 算法等.文献[5]提出一种加权KNN，算法实现简单，但定位时的时变特性带来的定位误差难以消除.所以出现了如贝叶斯算法的非确定性方法，减小了时变特性对定位结果产生的影响.但该算法需要大量数据进行全局搜索计算建立精确的概率模型，时间复杂度较高，所以在保证定位精度的同时降低时间复杂度成为贝叶斯室内定位算法研究的热点之一.文献[6]提出了基于CSI 贝叶斯室内定位方法，CSI 降低了多径效应产生的影响，但其只是简单的叠加了RSS和CSI 信号，不但增加了数据量而且大幅度降低了计算速度；文献[7]提出了以信号符合单高斯分布特性为前提的贝叶斯室内定位算法，提高了定位精度，但是CSI 信号的分布往往更加复杂，单高斯模型不能充分表示信号的分布特性；文献[8]提出了结合CNN 的贝叶斯室内定位方法，提高了定位精度，但也是以单高斯模型为前提来进行室内定位；文献[9]提出了结合加权KNN和贝叶斯算法进行定位，先根据加权KNN 选取子区域，再运用贝叶斯算法进行定位，虽然降低了计算速度，但是在选取k个参数求权值时，k值的选取具有主观性，并且KNN 对噪声点不敏感，噪声点的存在会对聚类结果产生较大影响，进而造成定位精度不高.

为了解决上述问题，本文提出了一种基于GMMDBC 的CSI 室内定位算法.首先，对CSI 数据进行预处理，根据处理后的数据进行模型参数的初次估计，并构建高斯混合模型(GMM)；提出确定分模型个数(DSM)策略，结合累积误差结果更新GMM 模型参数，得到CSI 最终分布特征；其次，基于不同参考点的CSI 分布特征，判断参考点间的紧密程度，将紧密相连的参考点划为一类，以此来确定每个子载波所在的簇；最后，根据分簇结果，利用贝叶斯概率算法进行权值计算，得到最终定位结果.

1 相关理论

所谓CSI 是利用正交频分复用(OFDM)技术将收发链路间子载波以CSI 的形式输出，它描述了信号在每条传输路径上的衰弱因子，如散射、环境衰弱、距离衰减等信息[10].CSI 以n×3×30的矩阵形式输出，n为数据的组数，可以根据实验需求进行采集，3 代表三根天线，30 代表30 个子载波.每个矩阵中的数据C以复数形式显示，即C=a+bi，a为实部，b为虚部.根据运算得到子载波的幅度|C|和相位 ∠C表达式为

图1为1 个数据包和100 个数据包不同子载波序列的幅度值对比图，由图1 可知，幅值上下波动幅度大体相同，信号相对稳定.图2为RSS和CSI 在相同参考点下的幅度值对比，CSI 选用的是任一子载波的幅度值.可以看出，在100 组数据对比下，CSI 比RSS 稳定.

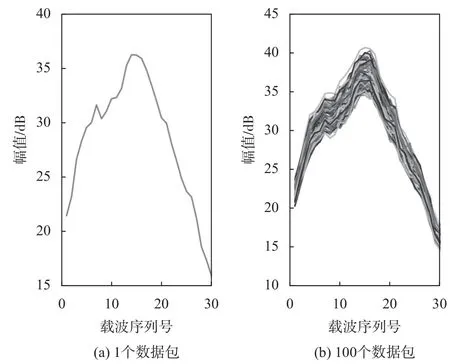
图1 不同数据包数量的CSI 幅度信息

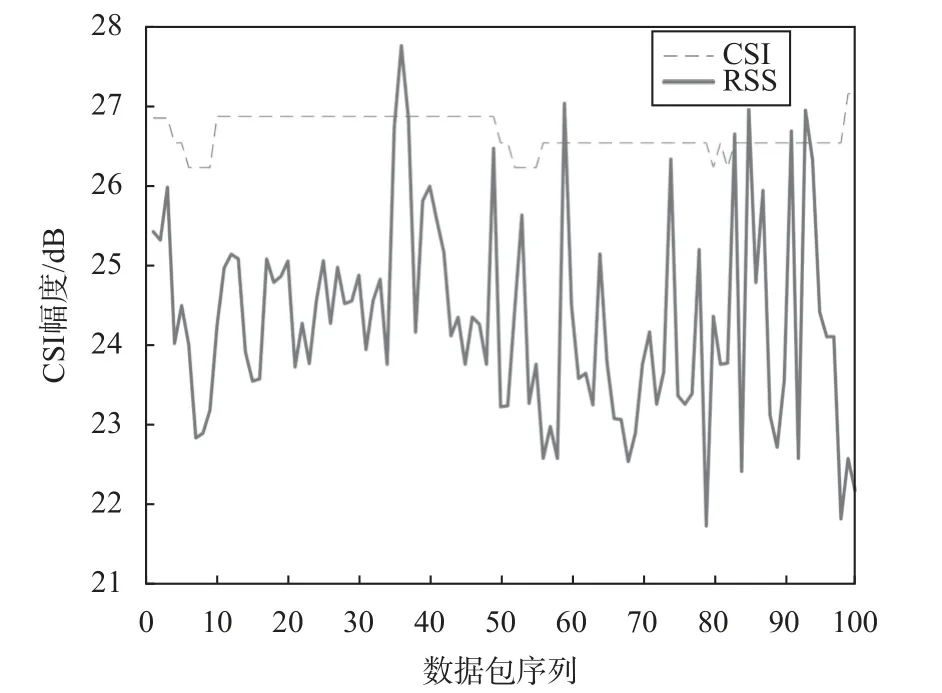
图2 RSS 与CSI 幅度值对比

虽然CSI 比RSS 稳定，但由于数据采集过程中存在一系列微小的随机波动，会造成异常值的产生.为了获得更加准确的定位结果，需要对异常值进行剔除.本文选用3σ准则对数据进行异常值的处理，通过计算得到期望 μ和标准差 σ，选取(μ-3σ，μ+3σ)作为标准，超出这个区间的即判定为误差，含有该误差的数据需要进行剔除.图3为剔除误差前后的对比，可以明显看出进行预处理后的数据更加的稳定.

图3 预处理前后对比

2 基于GMM-DBC 的定位算法

针对贝叶斯算法在进行室内定位研究中，存在定位精度较低，时间复杂度较高的问题，提出了一种基于GMM-DBC 的CSI 室内定位算法.图4为系统流程图.

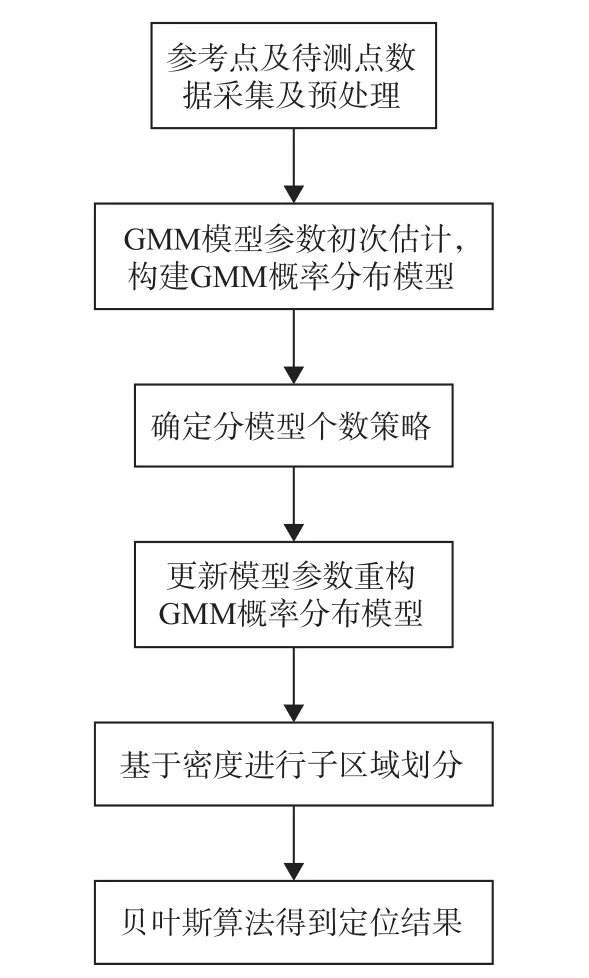
图4 系统流程图

算法步骤如下：

1)构建GMM 及参数估计

在运用贝叶斯算法确定权值的过程中，需要对输入CSI 数据的模型进行预测，预测的模型与真实的数据模型越吻合，计算得到的权值越准确，最终定位精度越高.所以本文引入GMM 对贝叶斯算法进行改进.GMM 是针对非均衡问题提出的一种概率增强算法[11]，由多个单高斯模型(GSM)混合而来的[12]，它保证了少数类数据集在平衡前后概率分布的一致性[13].由K个单高斯模型混合而成的混合高斯模型的概率分布为

式中：x=[x1,x2,···,xN]，为观测数据；N(x|μk,σk)为任意参考点的某一子载波训练形成的高斯混合模型中，第k个单高斯模型的概率密度函数，其服从期望为μk，标准差为 σk的正态分布；综上，需要估计的参数有，第k个高斯分布占的权重pk、均值 μk以及标准差σk.

为获得上述参数，本文选用EM 算法[14]进行求解计算.EM 算法分为两步，E是对似然函数求期望，目的是消去潜在变量.M是对期望求最大值.总体的迭代公式为

式中：θ=(p1,p2,···,pK,μ1,μ2,···,μK,σ1,σ2,···,σK)为所求的所有参数的集合；为第t次迭代的θ值；Q(θ,θt)为根据 θt所求的似然函数的条件期望，其中Q(θ,θt)的表达式为

式中：zi为属于某一高斯分布的概率，p(zi=ck)表示属于第k个高斯分布的概率；xl表示第l个子载波的完整的数据集，由,,···,组成，和之间相互独立，N=100 ；l ogP(|θ)为第l个子载波的第i个数据的似然函数，表达式为

P(zi|θt)为xi来自第k个高斯分布产生的后验概率，其公式为

代入到迭代式(3)可以求解出所求参数 θ的迭代公式为：

重复EM 算法直至 θ收敛，得到最终的估计值，将 θ代入式(2)，得到高斯混合模型.

2)确定分模型个数策略

EM 算法在估计参数时，除了需要确定各分模型初始参数外，还需要输入构成高斯混合模型的分模型个数.分模型个数的选择对定位误差的影响较大，如果模型个数选取较少，则达不到选用GMM 模型代替GSM 模型的目的，如果模型个数选取较多会大大增加算法的时间复杂度.

所以本文提出DSM 策略.首先根据参考点的数据，获取其期望值 μ1，标准差值 σ1，并作为建立模型的初值.然后初始化GMM 模型，设分模型个数K为1.把 μ1、σ1、K=1作为EM 算法的输入，求解出此时的GMM模型的概率分 布模型p(x1)，并根据p(x1)和求解出模型的累积误差E1，保存此时的误差为E′、K值为K′.令K=K+1，重复上述计算，求解得到累积误差EK.若EK＜E′，保存K′=K，E′=EK，直至K=4.通过对不同的参考点和不同的子载波的CSI 幅度进行模型的预测过程中发现，累积误差较小时的分模型个数在1～4.最终得到累积误差最小时的分模型个数K′.

重复上述计算，求出所有参考点的子载波的最终GMM 的概率分布模型.

3)子区域划分

为了解决贝叶斯算法进行全局搜索计算导致定位时间较长的问题，需要对不同子载波的参考点进行区域的划分.根据各个参考点之间的欧氏距离[15]，选取前t个距离最大点进而进行子区域的划分的传统方法，对t值的选取具有主观性，且在划分区域时噪声点的存在会对最终划分结果产生影响.所以本文引入基于密度的聚类算法[16-17]进行子区域的划分.

在相同子载波下，第i个参考点的均值 μi，标准差σi.第q个待测点的CSI 数据均值为 μq，标准差为 σq.在对第q个待测点的位置进行预测前，需要对其进行子区域的划分.M为参考点个数，加上待测点信息，共有M+1组(μ,σ)数 据，即((μ1,σ1),(μ2,σ2),···,(μM,σM)(μq,σq))作为输入数据集.

针对这组输入数据集，分别对期望和标准差进行子区域的划分.以每一个参考点期望和标准差为圆心，以两核心点之间的距离(Eps)为半径画一个圆的区域，这个区域被称为Eps邻域；统计在这个区域内的参数个数.如果区域内参数的数目超过了密度阈值(Mpts)，那么将这些参数记为核心点.将核心点的Eps邻域内的所有的核心点连在一起，这样不断地将区域内的核心点连在一起，形成一个簇.

对其余子载波做相同的处理，得到针对每个子载波所形成的簇.统计待测点q的每个子载波所在的簇的交集，作为最终确定待测点位置可能出现的参考点的集合.将这T个参考点作为下一步进行贝叶斯位置预测的计算点.通过上述运算，避免了全局搜索，降低计算量.

4)贝叶斯求解最终位置

贝叶斯算法[18]是一种从概率的角度看待定位问题的非确定性定位算法.通过求解测试点所有子载波的CSI 信息发生的后验概率，再通过后验概率与位置一一对应相乘求和，实现最终位置估计.结合上一步，最终定位的目标是在已知待测点q的CSI信号为xq=[xq1,xq2,···,xqN]的 前提下，预测q点的位置.所以需要分别计算在预测点信号为xq的前提下，在第t个参考点出现的概率[19]，目标公式为

式中：P(pt)为待测点q在第t个位置出现的概率，一般认为为等概率事件即P(pt)=1/T；分母P(xq)为信号xq出现的概率，P(xq)表达式为

式中，P(xq|pt)为待测点位置在第t个参考点的前提下，接收到的CSI 信号为xq的概率，因为xq由N个子载波构成，所以其表达式为

通过步骤2)对数据的整理，结合式(2)可以统计出第t个参考点的第i个子载波的CSI 幅度值的高斯模型表达式为

将式(11)和式(12)代入到式(10)中得到后验概率.对得到的t个后验概率P(pt|xqi)进行归一化处理，得到的值作为最后求解目标位置的权重系数.通过式(14)求解出最终的目标位置.

3 实验分析

3.1 实验环境布置

本实验采集数据环境为辽宁工程技术大学实验楼东304 室，面积约为140 m2，环境内包含通信实验器材、桌椅板凳、手机、电脑、投影设备等，设置80 个参考点(黑色圆点表示)，32 个测试点(黑色菱形表示)，参考点间隔90 cm，测试过程中路由器位置保持不变，图5为分布图，图6为真实场景图.

图5 室内分布图

图6 真实场景图

采集数据采用2.4 GHz和5.0 GHz 兼容的TPLink 路由器作为发送器，接收端是运行10.04LTS 本的笔记本电脑，系统是32 位Ubuntu Kinux，计算机通过其内置的三天线Intel 5300 半高内置网卡接收路由器发送的信道状态信息信号[20].采集数据时，首先连接路由器电源，保证路由器可以正常发送信号，打开计算机，移动计算机到待测点，保证计算机与路由器距离地面的高度一致，每个参考点在四个方向分别采集数据30 s，每个方向的数据取250 组，每个参考点获得1 000 组数据.

实验利用累积分布函数(CDF)、累积误差、平均定位误差和运行时间作为评价算法性能的指标.累积误差在利用公式对各部分计算结果进行累加时，其误差值也随之累加，最后所得到误差总和称为累积误差.累积分布函数，是概率密度函数的积分，能完整描述定位误差的概率分布.运行时间即算法的处理时间，一般被用来衡量算法的时间复杂度.

3.2 高斯混合模型分模型个数的选择

如表1 所示，为不同k值下的GMM 模型的累积误差.根据采集到的1 000 组数据，用直方图表示真实值的数据分布，与高斯混合模型的不同幅度值对应的概率密度值做差，将差值相加，得到累积误差值.序号1为第一个参考点的第15 个子载波，累积误差最小时对应的k值为2.序号2为第9 个参考点的第22 个子载波，可以看出累积误差最小的点在k=3.序号3为第4 个参考点的第2 个子载波，可以看出累积误差在k=4时最小.通过上述三组数据可以得出，在选择分模型个数时，应选择累积误差最小时的分模型个数.在实验过程中如果遇到在不同分模型个数下最小累积误差相同的情况，应选择模型个数少的进行计算.

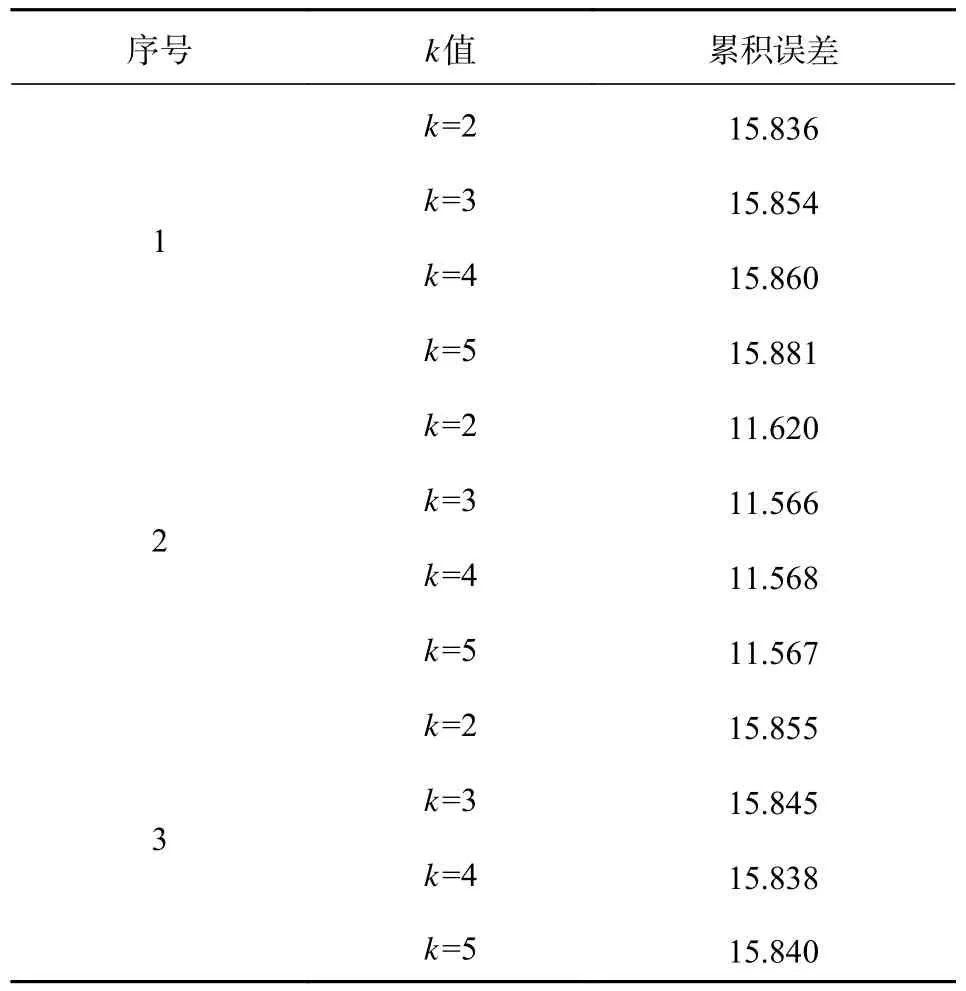
表1 k值对累积误差的影响

3.3 高斯混合模型与单高斯模型比较

根据EM 算法和DSM 决策，能够获取高斯混合模型的待估计参数 θ.如图7 所示，为第1 个参考点的第3 个子载波的CSI 幅度直方图、单高斯模型的概率密度函数和k=2时的高斯混合模型的概率密度函数对比图.

图7 CSI 直方图、GMM、GSM 分布曲线

图8为迭代次数与权重、期望、标准差之间的关系，可以看出，随着迭代次数的增加，期望值、标准差和权重值都趋于稳定，说明在迭代次数范围内可以得到准确的参数值.最后得到k=2时的高斯混合模型中，第一个单高斯模型的期望为14.24 dB，方差为0.39，权重为0.43；第二个单高斯模型的期望为12.61 dB，方差为0.84，权重为0.56.

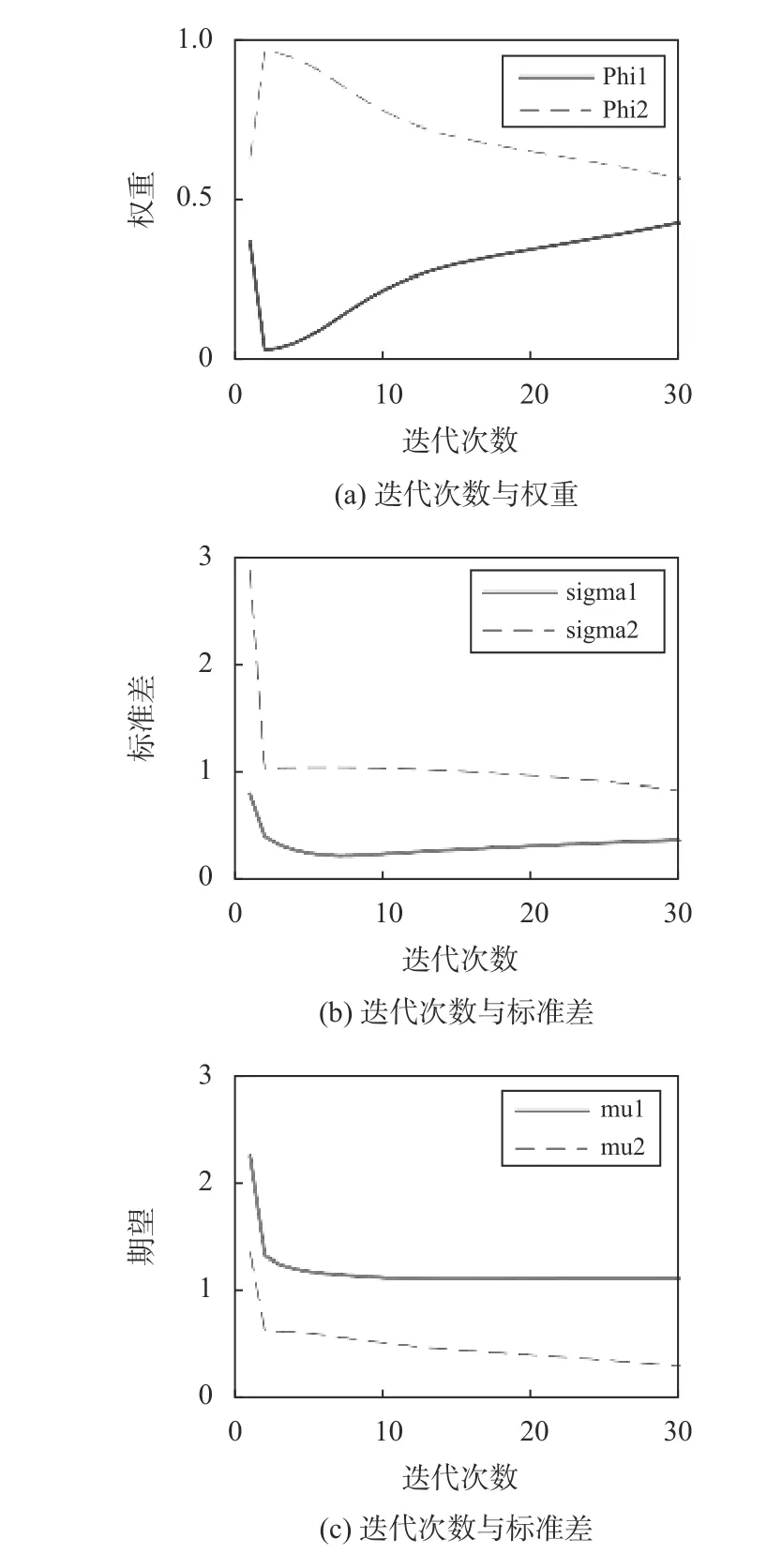
图8 迭代参数

在保证其他条件不变，只改变数据模型类型的情况下，根据式(14)得到预测的位置坐标，然后根据式(15)计算得到真实位置与预测位置之间的误差E.

式中：(,)为 预测点真实坐标；(,)为预测的位置坐标.根据E得到误差累积分布函数.在相同误差下，CDF 越大，定位精度越高，定位效果越好.

如图9为GMM和GSM 的误差的累积分布函数.定位误差在2 m 以内时，GMM 的累积概率分布达到了90%，同一误差下GSM 只能达到75%.并且利用GMM 进行定位的平均定位误差为1.012 3 m，与GSM 的1.458 4 m 相比，减小了0.446 1 m.根据上述数据及对比图可以看出GMM 比GSM 更好地描述信道状态信息的分布情况.

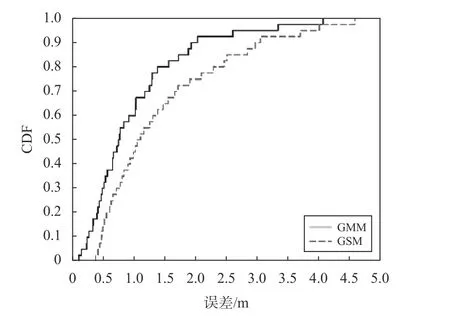
图9 GMM 与GSM 误差累积分布函数

3.4 不同定位算法比较

本文算法与传统贝叶斯算法、文献[8]中以单高斯模型为基础的CNN-贝叶斯室内定位方法、文献[9]提出的根据加权KNN 选取子区域室内定位的WKNN-贝叶斯定位方法在相同环境下进行对比分析，针对23 个测试点，根据式(14)和式(15)计算误差及累积概率分布验证算法性能.包括本文算法在内的四种算法的累积概率分布如图10 所示.

图10 不同定位算法的CDF

从定位精度来看，四种算法的累积概率分布都能达到95%以上.但当室内定位误差在2.75 m 以内时，本文算法的CDF为0.950，最先达到95%以上，CNN、WKNN-贝叶斯、传统贝叶斯算法的累积概率分布分别为0.875、0.825和0.775，均低于本文算法.如表2 所示，本文算法平均定位误差可以达到1.012 3 m，与CNN、WKNN-贝叶斯、传统贝叶斯比，分别降低了0.256 3 m、0.655 5 m、0.767 4 m.从定位时间来看，本文算法与CNN和传统贝叶斯算法相比都有大幅度下降，WKNN-贝叶斯算法虽然与本文算法定位时间接近，但是最大定位误差、平均定位误差均大于本文算法.综上，本文算法定位效果优于其他三个对比算法，在提高定位精度的同时，降低了时间复杂度.

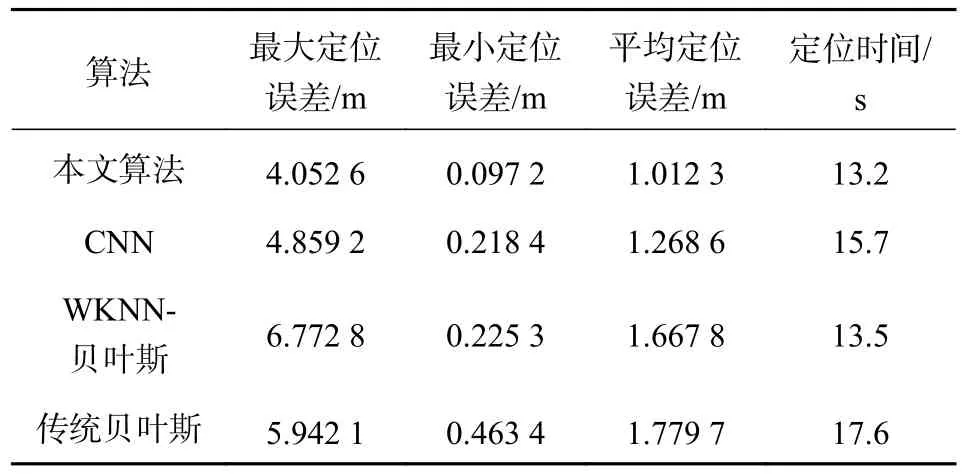
表2 不同方法定位精度对比

4 结论

本文提出一种基于GMM-DBC 的室内定位算法.引入GMM 对贝叶斯算法进行改进，并提出DSM策略进一步提高模型精度，进而减小定位误差.此外利用基于密度的聚类算法进行子区域的划分，解决了全局搜索计算导致的时间复杂度较高的问题.通过实验的验证，当该算法定位误差在2.75 m 以内时，误差累积概率分布为0.950，降低时间复杂度.本文研究虽有一定成效，但在多目标和移动目标定位方面仍然存在缺陷，后续将着重在这方面进行深入研究.

致谢：感谢首山聚创团体和李新春老师的讨论.