Comparison and quantitative assessment of two regional soil erosion survey approaches
2023-03-22LixiDongSuhuFuBoyunLiuBingYin
Lixi Dong , Suhu Fu , Boyun Liu ,b,*, Bing Yin
a Faculty of Geographical Science, Beijing Normal University, Beijing,100875, PR China
b Advanced Institute of Natural Sciences, Beijing Normal University at Zhuhai, 519087, PR China
c State Key Lab Soil Erosion and Dryland Farming on the Loess Plateau, Institute of Soil and Water Conservation, Northwest A&F University, PR China
Keywords:Regional soil erosion Soil erosion survey Grid approach Sampling approach CSLE
A B S T R A C T Regional soil erosion surveys are the first step of soil conservation planning.Grid and sampling approaches are commonly used for soil erosion surveys at the regional scale.With the grid approach, the region is divided into grids(e.g.,1 km×1 km),and the soil erosion rate of each grid was calculated.With the sampling approach, a small portion of the area (typically 4% or less) was taken and then the soil erosion rate was calculated.Based on the above calculation, both approaches evaluated the soil erosion area (which is the area where the soil erosion rate is greater than the soil loss tolerance (t)) and its distribution in the whole region.The purpose of this paper is to compare the assessment results of the two approaches and analyse their practicality using Yunyang County, Chongqing, China (area is 3636 km2).The soil erosion rate, percentage of soil erosion area (PSEA, which is the ratio of the area where the soil erosion rate is greater than the soil loss tolerance(t)to the area of the total study region)and its spatial distribution were compared between the two approaches.The results showed that the grid approach overestimated the average soil erosion rate and PSEA overall for all 33 sample units and the whole region in comparison to the sampling approach.The sampling approach can yield a reasonable spatial distribution of the soil erosion rate in the whole region.In addition,the soil erosion regions were more clustered than those using the grid approach, which can be more suitable for soil conservation planning.Therefore,the sampling approach is an efficient and practical approach in regional soil erosion surveys.The results can provide insights into regional soil erosion surveys.
1.Introduction
Soil erosion leads to soil degradation and environmental pollution, which influences the sustainable development of agriculture.Regional soil erosion surveys are the first step of soil conservation planning.There are two main types of soil erosion survey approaches at the regional scale: the grid-based surveys and sampling-based surveys, which are referred to as the grid and the sampling approach in this study, respectively.
With the grid approach,the region is divided into grids,and soil erosion model is applied to each grid to assess the erosion rate.The grid size, commonly 1 × 1 km and 30 × 30 m, etc., at present, is chosen based on the spatial resolution of available data such as the digital elevation model (DEM) and fractional vegetation cover(FVC).This approach is employed by Australia(Lu et al.,2001)and European Union countries (Grimm et al., 2002; Panagos et al.,2015).From 1997 to 2001, Australia adopted the grid approach for soil erosion surveys: the grid was divided across the country, and soil erosion rates were calculated using the RUSLE (Revised Universal Soil Loss Equation) (Renard, 1997) model with a 0.025°×0.025°grid.For EU countries,the USLE(Universal Soil Loss Equation)model(Wischmeier&Smith,1978)was used to calculate the soil erosion rate and to assess the potential and actual soil erosion risk.The potential risk calculations considered climatic,topographic and soil conditions without considering the cover and management factor (C) and support practice factor (P).The actual risk took into account C(i.e.,P=1).The monthly and annual rainfall erosivity values were calculated using the daily rainfall data from 578 rainfall stations in Europe during 1989-1998 and then interpolated onto a grid with a resolution of 1 × 1 km.Soil erodibility factor values were calculated using 1:1,000,000 soil data from Europe.Topographic factors were calculated using a DEM with a resolution of 1 × 1 km.The C factor was calculated using the normalized difference vegetation index (NDVI), and the P factor was assigned as 1.
With the sampling approach, soil erosion assessment was performed in a selected small proportion of the area by applying soil erosion model, with model parameters obtained through detailed field surveys and interpretation of remote sensing images.This approach has been used for soil surveys in the United States(Breidt&Fuller,1999;Nusser&Goebel,1997)and China(Liu et al.,2020).The soil survey in the United States was performed through the National Resources Inventory program conducted by the Natural Resources Conservation Service (Nusser & Goebel, 1997).The sampling approach of the United States has been continuously improved since the 1950s.The USLE model was first used to assess soil erosion in 1977, and by 1997, the soil survey was conducted every five years for a total of five times(Nusser&Goebel,1997).It has been conducted annually since 2000,based on the accumulated data, with a reduced sampling size and dynamic change monitoring.The sampling survey is performed using a stratified twostage unequal probability area sample (Nusser & Goebel, 1997).Stratification includes division of the country into four levels:county, township, section, and Primary Sample Unit (PSU).Twostage represents sampling is divided into two phases: in the first stage,the PSU is selected;in the second stage,sampling points are randomly selected in the extracted PSU.Unequal probability represents different sampling densities that are adopted when PSUs are extracted according to sections.Space represents the sampling points that are a parcel of a certain area.In China, a national soil erosion survey that consists of 32,364 sample units was completed in 2011 using a sampling approach(Liu et al.,2020)similar to that in the United States,but there were two main differences.One was that the survey objects in the United States were sampling points(plots),while those in China were sampling units(1×1 km grids in plain areas or 0.2-3 km2small watersheds in mountainous and hilly areas); second, the sampling points in the U.S.PSUs were randomly selected, while the sample units in the Chinese PSUs were systematically determined.The sampling approach in China was a stratified unequal probability systematic space sample.The stratification was performed in a fashion in which the country was uniformly divided into 4 levels: the first level was at the county level,in which the country was divided into 40×40 km townships.The second level was at the township level,in which each township was divided into 10 × 10 km sections.At the third level, each 10×10 km section was further divided into 5×5 km control areas.Finally,at the fourth level,a PSU with size of 1×1 km was located at the center of each control area.In the plain area,the PSU was the sample unit, whereas in the mountainous and hilly areas, a small watershed with an area of 0.2-3 km2was the sample unit, which needed to intersect with the PSU.Unequal probability was the difference in sampling density;for example,for sampling densities of 4%,1%, 0.25% and 0.0625%, the area of the sample units was 4%,1% and so on of the total area of the study area, respectively.By“systematic space”represents a PSU that was an area of certain size and was located at the center of each control area to avoid artificial influences such as choosing a PSU close to roads.
By comparing the above two approaches,we can learn that both approaches use soil erosion models to calculate soil erosion rates,such as the USLE, RUSLE or CSLE (Chinese Soil Loss Equation) (Liu et al., 2002), and the difference mainly lies in the method of obtaining soil erosion factors.The grid approach calculates soil erosion rates for every piece of land,30×30 m,for instance,but the accuracy is generally lower than that of the sampling approach.Because erosion factors cannot be obtained through cell-by-cell field surveys, vegetation and ground cover are mainly dependent on remote sensing data, the slope length and slope steepness factors generally use small-scale digital topographic maps or a coarse DEM, contour tillage and no-till conservation measures cannot be reflected,and some terraces may be missed.However,the sampling approach allows detailed erosion factors to be obtained through field surveys and the use of large-scale digital topographic maps or high-resolution DEM, and thus can calculate accurate soil erosion rates within the sample units.The disadvantage of the sampling approach is that soil erosion rates cannot be calculated for the entire area but only for the sample units,which is only 4%or less of the surveyed area.Regional assessment can only be achieved through spatial interpolation, which can introduce uncertainty.So in common sense, the gird approach can obtain a better spatial distribution of the soil erosion rate,and the sampling approach can obtain a better calculation of the soil erosion rate.
There are currently a number of studies on these two approaches separately.For the grid approach,the accuracy evaluation of the basic data sources is used for each erosion factor calculation,such as the accuracy evaluation of data on land use and engineering measures(Li et al.,2018;Yang et al.,2020),the effect of topographic factor data of different resolutions on soil erosion assessment (Fu et al., 2015a; Hessel, 2005; Li et al., 2021; Lu et al., 2020), etc.For the sampling approach, the effect of sampling density and interpolation methods is on regional soil erosion assessment(Yin et al.,2018; Zhang et al., 2018; Zou et al., 2016).However, no relevant research has been conducted on the comprehensive comparison of the two approaches.The questions we want to answer are, how accurate is the grid approach in comparison with the sampling approach? Can the sampling approach yield a reasonable and practical spatial distribution of the soil erosion rate in the whole region? Our hypothesis is that 1) the grid approach cannot accurately calculate the soil erosion rate,and 2)the sampling approach is not able to obtain a reasonable spatial distribution of the soil erosion rate.The purpose of this paper is to compare the assessment results of the two approaches for a county and analyse their practicality.The results can provide insights into regional soil erosion surveys.
2.Materials and methods
2.1.Study area
Yunyang County of Chongqing municipality is chosen as the study area,which located in southwestern China between latitudes of 30°35′6′′-31°26′30′′N and longitudes of 108°35′32′′-109°14′51′′E(Fig.1a).It covers an area of 3636 km2.It has a subtropical monsoon climate with an annual average precipitation of 1113 mm.Precipitation is concentrated from May to September, accounting for 73%of the annual total.The landform type is karst.The elevation in the area ranges from 139 m to 1809 m above sea level.The topography is inclined from the north to the middle area,with high mountains,deep valleys and steep slopes.The slope varies from 0°to 88°,with an average slope of 27°.

Fig.1.Location of the study area and an example of sample unit.(a)Distribution of sample unit and location of Yunyang County,(b)base maps of a sample unit for field survey,and(c) land use map of a sample unit with nine parcels and five categories of land use (1-farmland, 2-road, 3-forestland, 4-grassland and 5-construction land).
2.2.Data and processing
(1) Satellite image: Gaofen-1(GF-1) satellite images with 2.0 m resolution in Yunyang County in 2019 were used to interpret land use and soil conservation practices; Landsat 8 surface reflectance data for the three years from 2016 to 2018 with a spatial resolution of 30 m and a time resolution of 16 days were used to calculate the fractional vegetation cover(FVC).
(2) Rainfall erosivity and soil erodibility factors: these two factors were obtained by cutting Chinese maps using the boundaries of counties and sample units.Both maps were produced during the Chinese soil erosion survey with a 30 m resolution(Liu et al.,2020).The rainfall erosivity factor map was made based on daily erosive rainfall (daily rainfall≥10 mm) from 2881 rainfall stations in China.The soil erodibility factor map was drawn based on 7764 soil profiles in China.
(3) Topographic data:digital contour maps at a scale of 1:10000 were used for the sampling approach,and those at a scale of 1:50000 were used for the grid approach.The slope steepness and slope length factor were calculated using a tool developed by Fu et al.(2015b).
2.3.Two approaches for regional soil erosion survey and quantitative assessment
2.3.1.Grid approach
The Chinese Soil Loss Equation (CSLE) model (Liu et al., 2002)was used to assess regional soil erosion.The equation is:
where A is the soil erosion rate in t ha-1yr-1.R is the rainfall erosivity in MJ mm ha-1h-1yr-1.K is the soil erodibility in t ha h ha-1MJ-1mm-1.L and S are dimensionless topographic factors of the slope length and slope steepness, respectively.B, E and T are dimensionless factors of vegetation cover and biological practices,engineering practices and tillage practices, respectively (Liu et al.,2020).
In this paper,the R and K factors were taken from a Chinese map mentioned in Section 2.2 and then resampled to a 10 m resolution.L and S factors were calculated using a 1:50000 digital contour map.Grid-based R, K, L, and S factors were created with a grid size of 10 × 10 m.
B,E and T factors were calculated based on land use map,which were obtained by visually interpreting GF-1 satellite images.The B factor was mainly calculated based on the canopy cover and ground cover of forest,grassland and orchard.Canopy cover was calculated using FVC for 24 half months.Seasonal curves of 24 half months were drawn based on a field survey.Each curve represents the forest and orchard of one county by the grid approach.The calculation was also combined with the field survey results at the survey time.The sampling approach used field survey data for each parcel of forest and orchard.For details, refer to Liu et al.(2020).
Engineering measures were obtained by visual interpretation of GF-1 satellite images, and the E factor was assigned according to Table 1.The T factor was assigned a value of 0.424(Guo et al.,2015)based on the effects of single crop soil erosion ratios and 24 ratios of the average half-month erosivity to annual erosivity.
Finally,soil erosion rates were calculated in ArcGIS 10.2 software with seven raster layers of erosion factors.Each 10×10 m grid was identified as a soil erosion or non-erosion grid according to whether the soil erosion rate was greater than the soil loss tolerance(t)(Liu et al.,2020).The t value was 5 t ha-1yr-1in this study area according to a standard of the Ministry of Water Resources of PR China (2007).The soil erosion area is the area where the soil erosion rate is greater than the soil loss tolerance (t).The percentage of soil erosion area(PSEA)is the ratio of the area where the soil erosion rate is greater than the soil loss tolerance(t)to the area of the total study region.The soil erosion area and PSEA were calculated.
2.3.2.Sampling approach
(1) Sample design: based on the method of the national soil erosion survey of China completed in 2011(Liu et al.,2020),33 sample units were evenly distributed with a 1%sampling density (Fig.1a).
(2) Field survey: a field survey was conducted.First, the base maps for the field survey were made based on GF-1 satellite images, contour maps and sample unit boundaries (Fig.1b).Then,the boundary of the parcel with the same land use and engineering practice was drawn (Fig.1c).Finally, for each parcel, the land use, canopy cover, ground cover, and type and quality of soil conservation practices were surveyed and recorded.
(3) Calculation of the soil erosion rate:the soil erosion rate was calculated for each sample unit using the CSLE model,which was the same as that used in the grid approach, except that the L and S factors of the sampling approach was calculated using 1:10000 digital contour maps,while the grid approach was calculated using 1:50000 digital contour maps.The ground cover was determined by a field survey, while the grid approach was an average for the whole county.Furthermore, the land use and engineering practice data of the sample unit were more detailed.
(4) Interpolation:the soil erosion rate and PSEA were needed to interpolate from sample units to the whole region.
(a) Interpolation of the PSEA(PSEA-Interp).First,the weighting average PSEA for different land uses in each sample unit(PSEAsl) was calculated:
where PSEAsl(%)is the percentage of the soil erosion area for land use l of sample unit s; PSEAplis the percentage of the soil erosion area for parcel p of land use l in the sample unit;LUApl(km2)is the land use area of parcel p of land use l in the sample unit;and n is the number of land use l in the sample unit.
Then, the PSEA for each land use in the sample units was sequentially interpolated to the whole region using inverse distance weighting (IDW), and this interpolated result was clipped using regional land use boundaries.Finally, the PSEA of the whole region was obtained by merging clipped results together into a map.
(b) Depending on the level of detail or accuracy of the basic data used for each erosion factor calculation, different methods can be chosen to interpolate the soil erosion rate (Yin et al.,2018).In this study, two methods were employed to interpolate the soil erosion rate.With the first method, we used the average soil erosion rate (A) of each sample unit of each land use (A-Interp).First, the weighted average soil erosion rate for different land uses in each sample unit (Asl) was calculated:
where Asl(t ha-1yr-1)is the average soil erosion rate for land use l of sample unit s and Apl(t ha-1yr-1)is the average soil erosion rate for each parcel p of land use l in the sample unit.
Then,the soil erosion rate for each land use in the sample units was sequentially interpolated to the whole region using inverse distance weighting(IDW),and this interpolated result was clipped using regional land use boundaries.Finally, the soil erosion rate of the whole region was obtained by merging clipped results together into a map.

Table 1 Values of the E factor for engineering practices.
With another method,we used the product of five factors at each sample unit and for each type of land use: the slope length, slope steepness, biological, engineering and tillage factors (LSBET).In contrast, this method is denoted as LSBET-interp.The same calculation process as the method of A-Interp was used to obtain the LSBET product for the whole region, which was then multiplied by the R and K factors of the whole region to obtain the regional soil erosion rate.This method considered the same accuracy of the R and K factors of the sampling approach and the grid approach, without interpolation,and directly used the R and K of the whole region.
2.4.Data analysis
(1) Soil erosion rate and percentage of soil erosion area (PSEA)
The soil erosion rate and PSEA were obtained by four methods,two for the sampling approach and two for the grid approach.The sampling approach has high calculation accuracy of the soil erosion rate within sample units,so this is used to evaluate the calculation accuracy of the soil erosion rate for the grid approach.The four methods were as follows: (a) sample unit calculation, (b) interpolation the whole region result from sample unit calculation, (c)clipping by sample unit boundaries from the map of grid approach,and (d) grid approach calculation for the whole region.By comparing the four results, the accuracy of the sampling and grid approach in regional soil erosion surveys was analysed.
(2) Similarity of the spatial distribution of soil erosion rate
The grid approach has a better spatial distribution of the soil erosion rate,so this result was used to evaluate the reasonableness of the spatial distribution of the soil erosion rate of the sampling approach, as measured by the similarity index.In this study, the similarity index refers to the percentage of the number of cells or units assessed by the two approaches both as eroding or neither as eroding to the total number of cells or units studied.
To calculate the similarity index,five steps were taken.In step 1,the whole region was divided into 1 km2and 4 km2cells and small watershed units (7.52 km2on average) for similarity assessment.The reason for this division was that the size of the control area in soil conservation planning is generally 1-10 km2; therefore, we chose three sizes: small, medium and large.In step 2, calculate whether each 10× 10 m grid is accelerated erosion(erosion grid).In this step, the grid and sampling approaches were slightly different.For the grid approach, the soil erosion rate in each grid(10 × 10 m) was compared with the soil loss tolerance to distinguish whether it was an erosion grid.For the sampling approach,because the soil erosion rate cannot be calculated grid by grid(10×10 m)for the whole region,only the average soil erosion rate of sample units can be interpolated to the whole region.This rate cannot be used for erosion grid determination;therefore,the PSEA of each grid (10 × 10 m) was used to identify whether it was an erosion grid.For this purpose, the PSEA was ranked and then assigned as soil erosion grids from great to small one by one.This was continued until the total erosion area was equal to the soil erosion area calculated by the sampling approach, and the other grids were not soil erosion grids.In step 3,the PSEA for each 1 km2cell, 4 km2cell and small watershed unit was calculated and ranked.In step 4, the cells or units were assigned as soil erosion cells or small watershed units, one by one, according to the PSEA from great to small.This was continued until the total erosion area was equal to its own soil erosion area calculated by the grid and sampling approach, respectively, and the other cells or small watershed units were not soil erosion areas.In step 5,the similarity index was calculated.The results of step 4 for the two approacheswere compared accordingly.There were four possible scenarios for each cell or unit (Table 2), in which Scenarios 1 and 4 were considered identical, and Scenarios 2 and 3 were different.The percentage of the number of identical cells or units to the total number was the similarity index.

Table 2 Four scenarios of soil erosion cells or non-erosion cells.
3.Results
3.1.Soil erosion rate
The average soil erosion rates by the sampling and grid approaches of the sample units were 12.04 and 14.79 t ha-1yr-1,respectively, and the grid approach significantly overestimated by 22.8%(P=0.05)in comparison to the sampling approach(Table 3),although at some sample units,soil erosion rates estimated by the grid approach were lower than those by the sampling approach(Fig.2).Compared to the sampling approach, 21 (63.6%) sample units were overestimated and 12 (36.4%) sample units were underestimated by the grid approach,with two sample units being significantly underestimated (Fig.2) because farmlands with high erosion intensity were incorrectly interpreted as forestland or shrubland with low erosion intensity.The average soil erosion rates for the whole region calculated by the sampling approach were 15.41 and 15.62 t ha-1yr-1, while the grid approach was 17.24 t ha-1yr-1(Table 3);the relative differences were 11.88%and 10.37%, respectively.The results of the whole region were still overestimated by the grid approach,which was consistent with the results of the sample units.This indirectly showed that the sampling approach can reasonably calculate the soil erosion rate for the whole region.The average soil erosion rates of farmland and orchard were significantly different between the two approaches,which were 48.82 and 3.12 t ha-1yr-1respectively,by the sampling approach and 67.9 and 5.93 t ha-1yr-1, respectively, by the grid approach (Table 3).The grid approach overestimated farmland by 39.1% and orchard by 87.1% because the engineering practice investigated by the grid approach was not detailed.There was a small difference between the two approaches in the results of forest, shrub and grassland, and the relative difference was between -1.5 and 7.5%.In addition, the differences in the average soil erosion rates over the whole region obtained by A-Interp and LSBET-Interp were very small,with a relative difference of 1.3%,and the average erosion rates for each land use were also very close(Table 3).Therefore, among these two methods, A-Interp is recommended,because its calculation is simple,its expression form is straightforward, and it is relatively easy to understand.
3.2.Percentage of soil erosion area
The percentages of the soil erosion area(PSEA)by the sampling and grid approaches of the sample units were 37.0% and 47.4%,respectively (Table 4).The grid approach significantly overestimated by 28.1% (P = 0.00), although at some sample units, the estimated average PSEA by the grid approach was less than that by the sampling approach, with 24 (72.7%) of the sample units being overestimated and 9 (27.3%) being underestimated (Fig.3).The average PSEA for the whole region calculated by the twoapproaches were 39.5% and 50.3% (Table 4), respectively, and the relative difference was 27.4%.The results of the whole region were still overestimated by the grid approach,which was consistent with the results of the sample units.It can be seen that the sampling approach can assess the soil loss area in the whole region.There was a small difference between the two approaches in the results of farmland,shrubland and grassland,and the relative difference was between-5.9 and 7.5%.The average PSEA of orchard and forestland were significantly different between the two approaches, which were 28.6%and 22.7%,respectively,by the sampling approach and 46.6% and 49.9%, respectively, by the grid approach (Table 4).The grid approach overestimated the PSEA of forestland by 72.0% and that of orchard by 337.0%because the ground cover investigated by the grid approach was not detailed.In addition, some engineering measures in the orchard were not investigated.

Table 3 Soil erosion rate by the sampling and grid approaches for the sample units and the whole region.
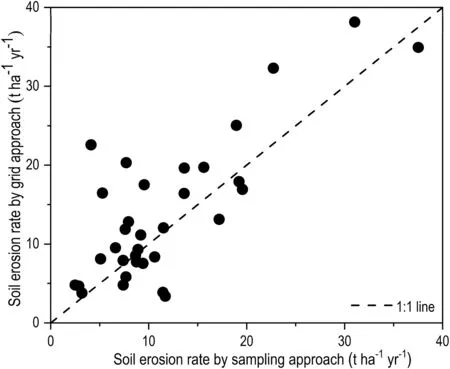
Fig.2.Soil erosion rate by the sampling and grid approaches of the sample units.
3.3.Spatial distribution of soil erosion
One purpose of regional soil erosion surveys is to determine where soil erosion areas are,which means that the soil erosion rate is greater than the soil loss tolerance.In general,the grid approach can obtain a better spatial distribution of the soil erosion rate.The spatial distribution of the soil erosion rate of the sampling approach similar to that of the grid approach was obtained when we interpolated the results of the sample units of the sampling method to the whole region.The similarity was 66.0%,68.0% and 71.1%at the scales of 1 km2cells, 4 km2cells and small watershed units,respectively.Moreover,compared with the grid approach,the areas of soil erosion in the sampling approach were more clustered(Fig.4),which can be more suitable for soil conservation planning.Therefore, the sampling approach can yield a reasonable and practical spatial distribution of soil erosion in the whole region.
4.Discussion
From the comparison of the two approaches, the sampling approach can yield a reasonable spatial distribution of the soil erosion rate in the whole region,which goes against the hypothesis two.Soil erosion assessed by the grid approach was overestimated on average,despite some grids were underestimated,which lends support for the hypothesis one.This was because some input data were not detailed or accurate, mainly including topographic, land use and soil conservation measures.
(1) Topographic data
The average slope steepness and slope steepness factor were 26.13°and 5.19 for the sampling approach and 21.93°and 4.47 for the grid approach (Table 5).The average slope length and average slope length factor were 57.93 m and 1.64 for the sampling approach and 121.32 m and 1.90 for the grid approach,respectively(Table 5).The grid approach underestimated the slope steepness and overestimated the slope length, underestimating the slope steepness factor by 13.79% and overestimating the slope length factor by 15.79%.The combined action of the slope steepness and slope length factor would reduce the error of the LS factor by the grid approach.The 1:1 scatter plot showed a good correlation of the LS factor between the grid and sampling approach (R = 0.83,p = 0.00) (Fig.5).Compared with the sampling approach, the grid approach underestimated the LS factor when the LS factor was small and overestimated it when the LS factor was large.In turn,soil erosion could be underestimated or overestimated.The average LS factor was 8.85 for the sampling approach and 9.07 for the grid approach.The average LS factor was overestimated by 2.4% by the grid approach in comparison to that with the sampling approach.On average for all sample units, soil erosion was overestimated by the grid approach.In relevant studies, compared with 1:10000 digital contour maps, Lu et al.(2020) found that the average LS factor was overestimated by 0.17%based on a 1:50,000 topographic map in Southwest China.Li et al.(2021)found that soil erosion was overestimated by 4.43% based on 1; 50,000 topographic maps in mountainous areas of Huailai County.However, it may not always be similar to this in other places (Wang et al., 2020).

Table 4 Percentage of soil erosion area(PSEA) by the sampling and grid approaches for the sample units and the whole region.
(2) Land use
Land use in Yunyang County was mainly forestland,shrubland and farmland, followed by orchard, grassland and others.The percentage of farmland and other land use is closer between the two approaches.The percentage of orchard for the grid approach was lower than that for the sampling approach because the orchards were difficult to be distinguished in satellite images.Compared with the sampling approach, the percentage of forest was smaller and shrubland was larger for the grid approach (Table 6).The absolute differences were -10.88% for forest and 11.95% for shrubland, because the two land uses were difficult to be distinguished when the satellite image resolution was coarse.In relevant studies,Li et al.(2018)found that the interpretation accuracies of forest and shrubland were very low,only 78.6%and 68.2%,respectively.Yang et al.(2020) also found that the interpretation accuracies of forest and grassland were low.
(3) Soil conservation practices
The main types of engineering practices in Yunyang County were bench terraces and terraces with slopes.The percentages of terraces (12.6%) and terraces with slopes (10.9%) by the sampling approach were 1.31 and 1.27 times higher than those of the grid approach, respectively.This result was consistent with the conclusions of Li et al.(2019),who found that the percentages of bench terraces and inward sloping terraces obtained from the field survey were twice as high as those from the visual interpretation of satellite images.A field survey found that some engineering practices could not be correctly visually interpreted based on satellite images due to the coarse resolution.The grid approach did not adequately assess the effects of engineering practices and therefore overestimated soil erosion.
The difference in biological practice factors between the two approaches was mainly because of the ground cover.The ground cover in the sampling approach used field survey data for each parcel, while that in the grid approach was calculated considering the average condition of the whole region.The B values of orchards obtained by the sampling and grid approaches for the sample units were 0.026 and 0.023, respectively, and the grid approach underestimated by 11.5%.Ground cover of orchards is greatly influenced by management practices, and the corresponding values vary considerably.The B-factor for the orchard using the grid approach was not correctly calculated for some parcels with extremely low ground cover.The B values of forestland obtained by the sampling and grid approaches for the sample units were 0.012 and 0.014,respectively.The grid approach overestimated by 16.7% due to underestimated high ground cover for some parcels.A field survey of the ground cover value of each parcel for the whole county is unrealistic in terms of time and funds.Du et al.(2021) used nonphotosynthetic vegetation (NPV) data for the ground cover value,but the calculation accuracy and universality of the data were unknown.Therefore, improving the calculation accuracy of ground cover and verifying it with more measured data require further research.
Compared with the sampling approach, the grid approach is time-consuming and labor-intensive.In this study,taking the visual interpretation of satellite images as an example, the grid method needed to interpret the whole area(3636 km2), which was a large workload, while the sampling method only interpreted sample units(7.86 km2),which was a much smaller workload than the grid approach.In addition, the input data of each factor of the grid approach were not detailed or accurate, which led to the low accuracy of soil erosion rate estimation.The sampling approach saves time and effort, and can yield a reasonable spatial distribution of the soil erosion rate in the whole region.Therefore, the sampling approach is an efficient and practical approach in regional soil erosion surveys.However, with the progress of science and technology, the grid approach can be widely applied and promoted when the accuracy of the input data of each factor for the whole region is high enough.
One county was selected for this study, and counties with different types of landscapes should be selected to continue the study in the future.In addition,the density of sample units in this study was relatively small,at 1%,and the interpolation accuracy of the sampling approach was tested by an indirect method(similarity index).In the future, more sample units can be selected and more detailed cross-validation can be performed to better validate the accuracy of the interpolation of the sampling approach.
5.Conclusion
Compared with the results of the sampling approach, the grid approach overestimated the average soil erosion rate and percentage of soil erosion area(PSEA)overall for the sample units and the whole region,which lends support for the hypothesis one.The sampling approach can yield a reasonable spatial distribution of soil erosion rate in the whole region,which goes against the hypothesis two.In addition, the soil erosion areas were more clustered than those by the grid approach, which was more suitable for soil conservation planning.Therefore,the sampling approach is an efficient and practical approach in regional soil erosion surveys.
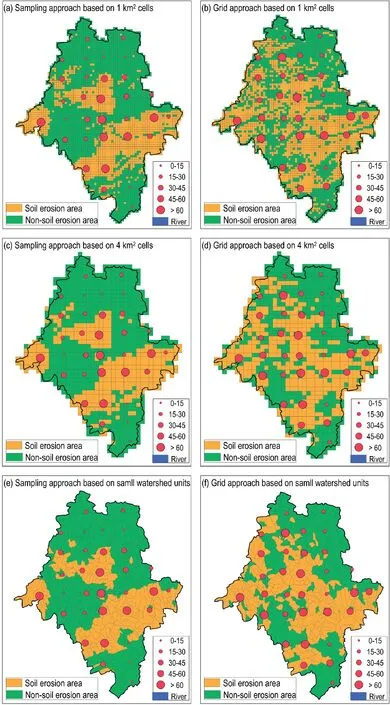
Fig.4.Spatial distribution of soil erosion area and percentage of soil erosion area by the sampling and grid approaches based on 1 km2 and 4 km2 cells and small watershed units.Circles of different sizes represent the percentage of soil erosion area.
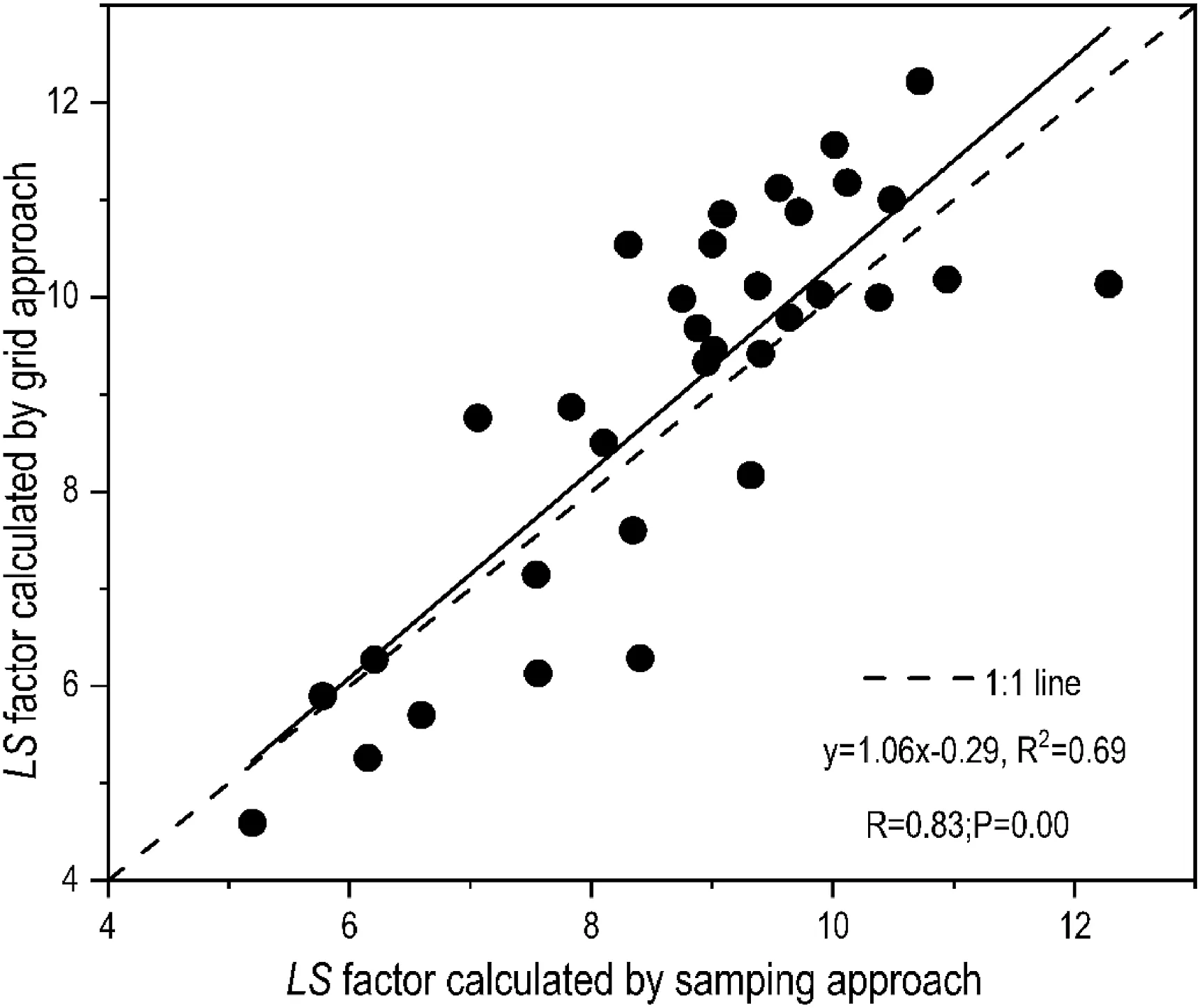
Fig.5.LS factor calculated by the grid and sampling approaches of the sample units.

Table 6 Land use of the sampling and grid approaches of the sample units.
Declaration of competing interest
The authors declare no potential conflict of interest.
Acknowledgements
This work was supported by the National Key R&D Project of China (2021YFD1500704).
杂志排行
International Soil and Water Conservation Research的其它文章
- Atlas of precipitation extremes for South America and Africa based on depth-duration-frequency relationships in a stochastic weather generator dataset
- Saturation-excess overland flow in the European loess belt: An underestimated process?
- Streamflow prediction in ungauged catchments by using the Grunsky method
- Towards a better understanding of pathways of multiple co-occurring erosion processes on global cropland
- Calibration,validation,and evaluation of the Water Erosion Prediction Project (WEPP) model for hillslopes with natural runoff plot data
- Long-term trends of precipitation and erosivity over Northeast China during 1961-2020
