基于改进卡尔曼滤波的叉车载重快速准确估计方法
2023-03-22黄泽雄黄运保李海艳黄东华
黄泽雄 刘 兰 黄运保 李海艳 黄东华
1.广东工业大学机电工程学院,广州,510006 2.广东技术师范大学网络空间安全学院,广州,510655
0 引言
在生产贸易活动中,对货物进行搬运和计重是货物估价必不可缺的环节。伸缩臂叉车作为货物搬运作业最为有效的工程机械之一,不但具备平衡重式叉车搬运货物的功能,而且在车身不动的情况下,可以通过伸缩臂伸缩和臂架变幅等操作进行不同高度与距离下的装卸作业,从而被广泛应用于农业、建筑业和港口装卸等领域[1-2]。而现有伸缩臂叉车主要通过转运过秤的开环反馈方式[3]对所装卸的货物进行估计,效率低下,且需要花费大量的人力物力。
在工程机械载重估计研究领域,目前国内外相关研究主要集中在挖掘机、门座起重机和吊车等工程机械,而对伸缩臂叉车载重估计方面的相关研究目前还未见报道。在国外,MINTAH等[4]于2012年提出了一套液压挖掘机自适应载重监控方案,该方案虽然能够实现载重自适应估计,但由于有效测量范围划分比较难控制,在实际应用中会受到限制。WALAWALKAR等[5]于2016年提出了一种基于测量方式的挖掘机载重估计方法,但是该种方法需要了解工作附件的惯性参数,并且其数学模型的求解较为复杂。为此,WALAWALKAR等[6]于2018年通过估计工作附件的质量、质心和质量惯性矩等参数对载重估计方法进行了改善,但是该方法对关节角加速度和动臂惯性参数的计算要求很高。PALOMBA等[7]于2019年提出了一种基于状态估计的载重估计方法,该方法是基于挖掘机运动学和动态模型的两阶段方法进行估计的,从而需要较多种类的传感器。在国内,温建明[8]于2008年提出了一套基于模糊神经网络的门座起重机载重动态估计方案,但该方案是在假设门座起重机匀速提升货物的理想化状态下进行估计的,且该系统的载重估计误差达到了5%。李婷婷[9]于2017年提出了一种考虑载重重心偏移和考虑地面坡度的叉装车自动载重估计算法,该算法能够有效消除动臂举升速度、载重重心偏移和地面坡度对载重估计结果的影响。但该算法仅适用于典型的反转六连杆机构,对于不同的叉装车工作装置结构,需要对载重估计数学模型进行较大的改动。何经旺[10]于2015年结合挖掘机的结构特点和工作环境的特殊性,根据Kane动力学理论的动力学和运动学,建立了液压挖掘机的载重估计数学模型,然后使用递推最小二乘算法进行载重动态估计。该方法可以在液压挖掘机的任何姿态下估计出铲斗载重大小,但因为其数学模型需要辨识转动惯量等变量,而转动惯量的辨识又会涉及到挖掘机各个杆件的实时重心位置,所以在实际作业中很难进行动态准确估计。
国内配备有载重估计技术的工程机械的估计系统在准确度和稳定性控制等方面都与国外产品有较大的差距,虽然已经研发了一些估计模型,但计算过于复杂且硬件成本昂贵,目前还没有一个可靠且有效的载重动态估计模型。研究一套伸缩臂叉车载重估计方案对国内工程机械智能制造和实现碳达峰、碳中和目标,以及智能化和无人化的货物搬运场景都具有重大的意义。
本文根据伸缩臂叉车工作装置的工作原理和臂架结构的组成特点,对臂架进行动力学分析,建立载重与液压系统压力、臂架变幅角度以及伸缩臂伸缩长度之间成线性关系的载重估计数学模型,然后使用具有实时辨识递推特点的卡尔曼滤波算法[11]对该模型进行求解。最后,针对卡尔曼滤波算法在递推过程中载重发生改变时新测量数据对载重估值失去校正能力的缺点,本文提出了一种基于改进卡尔曼滤波的载重估计算法。目前该载重动态估计方法已初步应用到某企业的超长重载伸缩臂叉车。
1 载重估计方案分析
本文研究了超长重载伸缩臂叉车,实车如图1所示,其尺寸和性能参数如表1所示。

图1 超长重载伸缩臂叉车Fig.1 Super long and heavy load telescopic handler
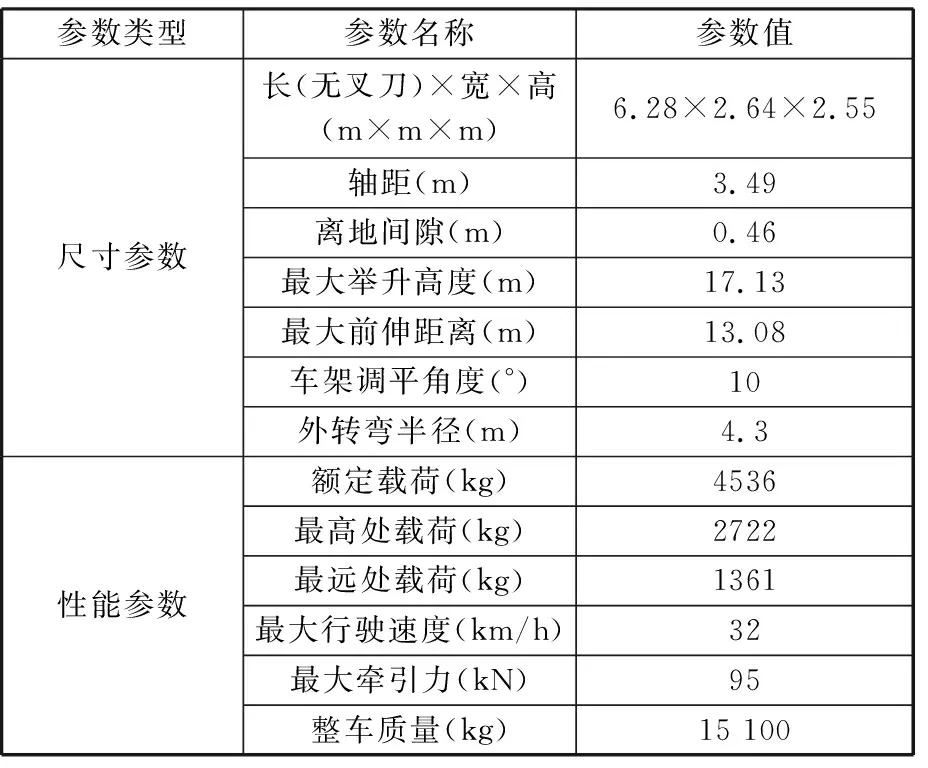
表1 伸缩臂叉车的尺寸和性能参数
1.1 基于动力学转动定律间接估计
根据一些已有的工程机械工作载荷估计方案,结合伸缩臂叉车的工作原理,提出了如下三种工作载荷估计方案:
(1)采用机械轴式传感器直接估计,在伸缩臂叉车第四级臂与货叉的支撑铰链处安装压力传感器,然后在某个固定姿态下,通过对测得的传感器信号进行运算处理,直接对载重进行估计;
(2)基于静力学力矩平衡原理[12]间接估计,将臂架固定在某个确定的变幅角度,用位移传感器和压力传感器分别静止采集伸缩臂伸缩长度、变幅液压缸和随动液压缸有/无杆腔压力,利用静力学力矩平衡原理建立载重估计数学模型,间接对载重进行估计[13];
(3)基于动力学转动定律[14]间接估计,与第二个方案不同,该方案是在作业过程中动态采集臂架变幅角度、伸缩臂伸缩长度、变幅液压缸和随动液压缸有/无杆腔压力,然后根据动力学转动定律建立的函数关系式,实现动态载重估计。
对各方案进行比较分析:方案(1)虽然以直接测量的方式能够实现载重动态估计,且估计准确度高、成本低。但是在作业环境恶劣、叉具频繁更换,以及轴销旋转时压力传感器会受旋转力作用的情况下,容易导致压力传感器失效和损耗,在实际应用中会存在故障率高、使用寿命短和局限性大等问题[15];方案(2)理论上能达到较高的称重精度,但需要静态测量,作业效率较低;方案(3)所建立的载重估计数学模型具有较强的实用性和较高的估计准确度,被目前工程机械载重估计领域应用得最为广泛[16-17]。
综合比较以上三个载重估计方案的优缺点,最终确定采用第三个方案,在不额外增加其他类型传感器的情况下,利用叉车工作装置现有功能模块中已装配的角度传感器、位移传感器和压力传感器实现叉车载重动态估计。
1.2 建立载重估计数学模型
为了简化力学分析和几何分析,假设臂架中心面与底盘纵向中垂面重合,将组成臂架的所有构件都置于这一平面坐标系内,以臂架与车架的回转销轴铰接点O为坐标原点,沿伸缩臂叉车行驶的水平方向为X轴正向,垂直于X轴的竖直向上方向为Z轴正向。将伸缩臂处于全缩回且处于水平状态的位置设为臂架的初始位置。假设各构件均为均质材料,其几何中心即重心,则构件的重心相对于X轴正向的变幅角度定义为Δθ,除此之外,还假设重心只沿变幅角度Δθ的射线上偏移。伸缩臂叉车的载重估计力学模型简图见图2,其中,O为臂架与车架的铰接点;J为变幅液压缸缸杆与基本臂的铰接点;S为变幅液压缸缸筒与车架的铰接点;M为随动液压缸缸杆与基本臂的铰接点;N为随动液压缸缸筒与车架的铰接点;F为四级臂头部与货叉的铰接点。
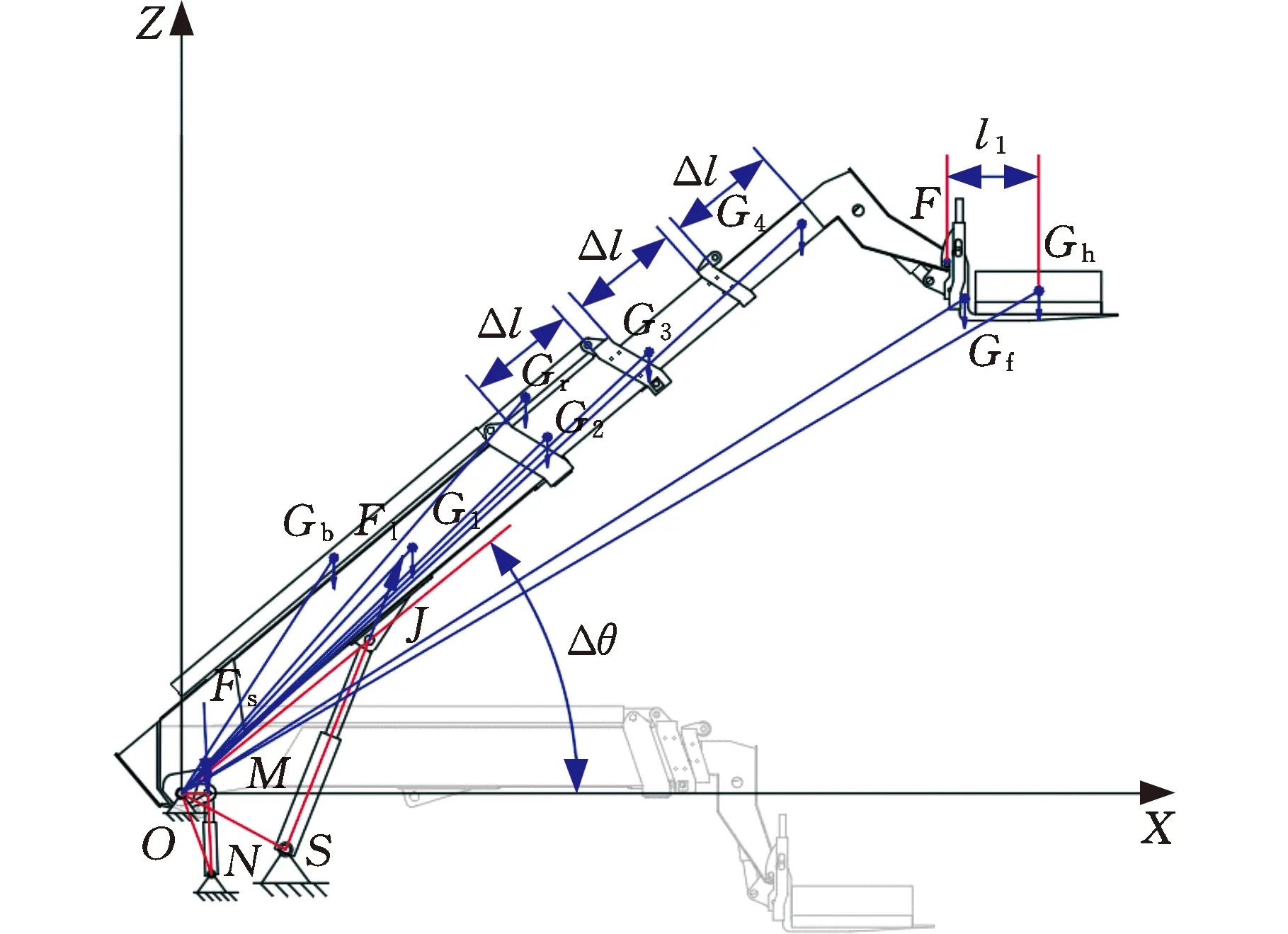
图2 伸缩臂叉车的载重估计力学模型简图Fig.2 Mechanical model diagram for load estimationof telescopic handler
在计算臂架自重对转动轴的力矩时,若直接将四个节臂、伸缩液压缸、调平液压缸、摇杆、连杆、货叉和连接件作为一个整体分析,当叉车进行变幅和伸缩等操作时,其整体重心位置就会难以确定。所以,这里采用离散化的思想,将臂架分成几个主要构件,然后逐个分析臂架伸缩变幅时各主要构件重心的运动规律。
由于叉车工作装置部分在正常工作时,基本臂是通过一根水平销轴与车架松连接的,故臂架受到车架对其支承力的作用可以忽略不计,而摩擦力和调平液压缸对货叉的推力作为臂架的内力则不计算在内。臂架在车身纵截面XOZ内会受到变幅液压缸的作用力Fl、随动液压缸的作用力Fs、载重重力Gh和臂架中各主要构件的自身重力。由于伸缩臂叉车在起吊的时候必须打开支腿且不能移动,因此伸缩臂只能在变幅角度内运动,水平惯性力几乎没有。再进一步忽略惯性较小的调平液压缸等构件对臂架动力学性能的影响后,伸缩臂叉车臂架绕定轴转动的微分方程为
JMα=FlLl+FsLs-G1L1-G2L2-
G3L3-G4L4-GbLb-GrLr-GfLf-GhLh
(1)
式中,JM为臂架对转动轴的转动惯量;α为臂架的角加速度,即对臂架变幅角度Δθ求时间的二阶导数;G1、G2、G3、G4、Gb、Gr、Gf、Gh分别为基本臂、二级臂、三级臂、四级臂、伸缩液压缸缸筒、伸缩液压缸缸杆、货叉以及载重的重力;L1、L2、L3、L4、Lb、Lr、Lf、Lh分别为相对应构件重力对转动轴的力臂;Fl、Fs分别为变幅液压缸和随动液压缸对臂架的作用力;Ll、Ls分别为变幅液压缸和随动液压缸作用力对转动轴的力臂。
对式(1)进一步分析,在合外力矩给定的情况下,刚体的转动惯量越大,则所获得的角加速度越小,即角速度改变得慢,刚体保持原有转动状态的惯性就越大。考虑臂架在变幅伸缩动作的起始加速和终止减速阶段,其角加速度α较大,会对载重估计有影响,但伸缩臂叉车臂架的转动惯量也大,且在变幅伸缩过程中大部分时间内都是处于稳定阶段的。所以一般认为臂架在货物变幅升降过程中其角速度是不变的,或者说角加速度几乎为零。这时,则可以忽略角加速度α的影响,从而避免臂架中各构件因质量和重心位置的不准确而造成动力学中关于转动惯量的复杂计算[18]。故有合外力矩∑MT=0,则式(1)等价于:
G1L1+G2L2+G3L3+G4L4+GbLb+GrLr+
GfLf+GhLh=FlLl+FsLs
(2)
如图3所示,计算变幅液压缸推力对转动轴的力臂。先根据余弦定理,计算出变幅液压缸上铰接点J到变幅液压缸下铰接点S的距离lJS,然后用面积公式计算三角形ΔJOS的面积,最后根据同一三角形面积相等,即可计算变幅液压缸推力对转动轴的力臂Ll,其表达式为
(3)
θl=θOJ+|θOS|
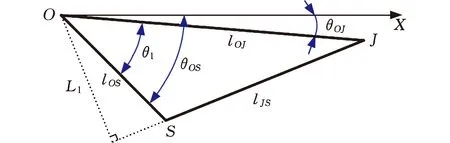
图3 变幅液压缸对转动轴的力臂Fig.3 Luffing hydraulic cylinder to the rotatingshaft force arm
式中,lOJ为臂架处于水平状态时,变幅液压缸上铰接点J到转动点O的距离;lOS为变幅液压缸下铰接点S到转动点O的距离;lJS为臂架处于水平状态时,变幅液压缸上铰接点J到变幅液压缸下铰接点S的距离;θl为臂架处于水平状态时,变幅液压缸上铰接点J、下铰接点S与转动点O形成∠JOS的角度;θOJ为臂架处于水平状态时,lOJ与X轴之间的初始角度;θOS为lOS与X轴之间的角度。
随动液压缸阻尼力对转动轴的力臂Ls也可根据式(3)同理计算得到。根据各臂架中各主要构件的几何结构及其重心位置的平面坐标关系,将求解得到的有关量代入式(2),再对该式的左边分离出变量臂架变幅角度Δθ和伸缩臂伸缩长度Δl可得到以下关系式:
a1cosΔθ-a2sinΔθ+a3ΔLcosΔθ+a4=
(4)
式中,a1、a2、a3、a4为未知参数;lOM为臂架处于水平状态时,随动液压缸上铰接点M到转动点O的距离;lON为随动液压缸下铰接点N到转动点O的距离;lMN为臂架处于水平状态时,随动液压缸上铰接点M到随动液压缸下铰接点N的距离;θs为臂架处于水平状态时,随动液压缸上铰接点M、下铰接点N与转动点O形成∠MON的角度。
进一步将式(4)化简成矩阵的形式:
Φ·Θ=MT
(5)
Φ=[a1a2a3a4]
Θ=[cosθ-sinθΔlcosθ1]T
式中,MT为变幅液压缸压力和随动液压缸压力对臂架的合外力矩。
根据式(4),在伸缩臂叉车处于空载的情况下,即Gh=0时,采集数学模型所需的全部可测变量:臂架变幅角度Δθ,伸缩臂伸缩长度Δl,以及变幅液压缸和随动液压缸有/无杆腔的压力plb、plr、psb、psr,然后将信号数据截取有效区间部分,即可辨识出四个未知参数:a1、a2、a3、a4。
将计算得到的载重重力对转动轴的力臂代入式(5),即可求得出载重重力Gh与臂架变幅角度Δθ、伸缩臂伸缩长度Δl,以及变幅液压缸和随动液压缸有/无杆腔的压力plb、plr、psb、psr之间的函数关系,即载重计算公式为
LhGh=MT-Φ·Θ
(6)
2 基于改进卡尔曼滤波的载重估计数学模型求解算法
参数估计法[19]可以将载重估计作为一个参数估计和预测问题进行辨识递推,本质上可以看作是载重估计模型辨识及其参数估计问题:将载重估计过程作为一个参数辩识的问题来处理,根据已经建立好的载重估计数学模型,推导出一个含有未知参数的模型,然后用该模型去拟合载重估计过程的输出信号,从而获得最小均方误差意义上的参数估计[20]。
卡尔曼滤波算法属于模型辨识与参数估计方法中的一种,该算法采用辨识递推的方式,只需在上一次结果的基础上进行下一步的运算,不需要将数据进行储存,且运算量小,适用于实时过程,可以用来估计只能被系统本身间接或不精确测量的状态变量。
卡尔曼滤波算法的方程分为两组:预测更新方程和测量更新方程[21-23]。在预测更新阶段,利用前一时刻的状态估计值对当前时刻状态进行估计;而在测量更新阶段,则利用当前时刻状态的测量值修正预测更新阶段的预测值,以获得一个更为精确的当前时刻状态估计。
将载重重力Gh作为该载重估计系统t时刻的状态变量;在该估计过程中默认前后两个时刻的载重不发生改变,即相邻两个时刻的状态并无切换,所以将状态转换参数A设置为1;由于系统中无控制信号输入,故将控制信号U(t)设置为0,控制状态参数B也设置为0。则预测更新方程可表示为
(7)
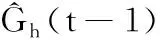
在预测更新阶段,还需要计算t时刻的先验估计误差协方差P-(t):
P-(t)=P(t-1)+Q
(8)
式中,P(t-1)为t-1时刻的后验估计误差协方差;Q为过程误差W(t)的协方差。
将载重计算公式作为估计过程的测量更新方程:
Z(t)=Lh(t)Gh(t)+V(t)=MT(t)-
Φ·Θ(t)+V(t)
(9)
Θ(t)=[cos(θ(t)) -sin(θ(t)) Δl(t)cos(θ(t)) 1]T
式中,V(t)为测量误差。
在测量更新阶段,首先需要根据预测更新部分得到的t时刻先验估计误差协方差P-(t)和测量误差V(t)的协方差R计算出t时刻的卡尔曼增益K(t):
(10)
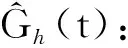
(11)
最后,还需要根据t时刻的先验估计误差协方差P-(t)和卡尔曼增益K(t)得到t时刻的后验估计误差协方差P(t):
P(t)=(1-K(t)Lh(t))P-(t)
(12)
基于卡尔曼滤波的载重估计算法流程如图4所示,可以看出,随着辨识递推的进行,当后验估计误差协方差P(t)减小至0时,载重估计过程将停止。
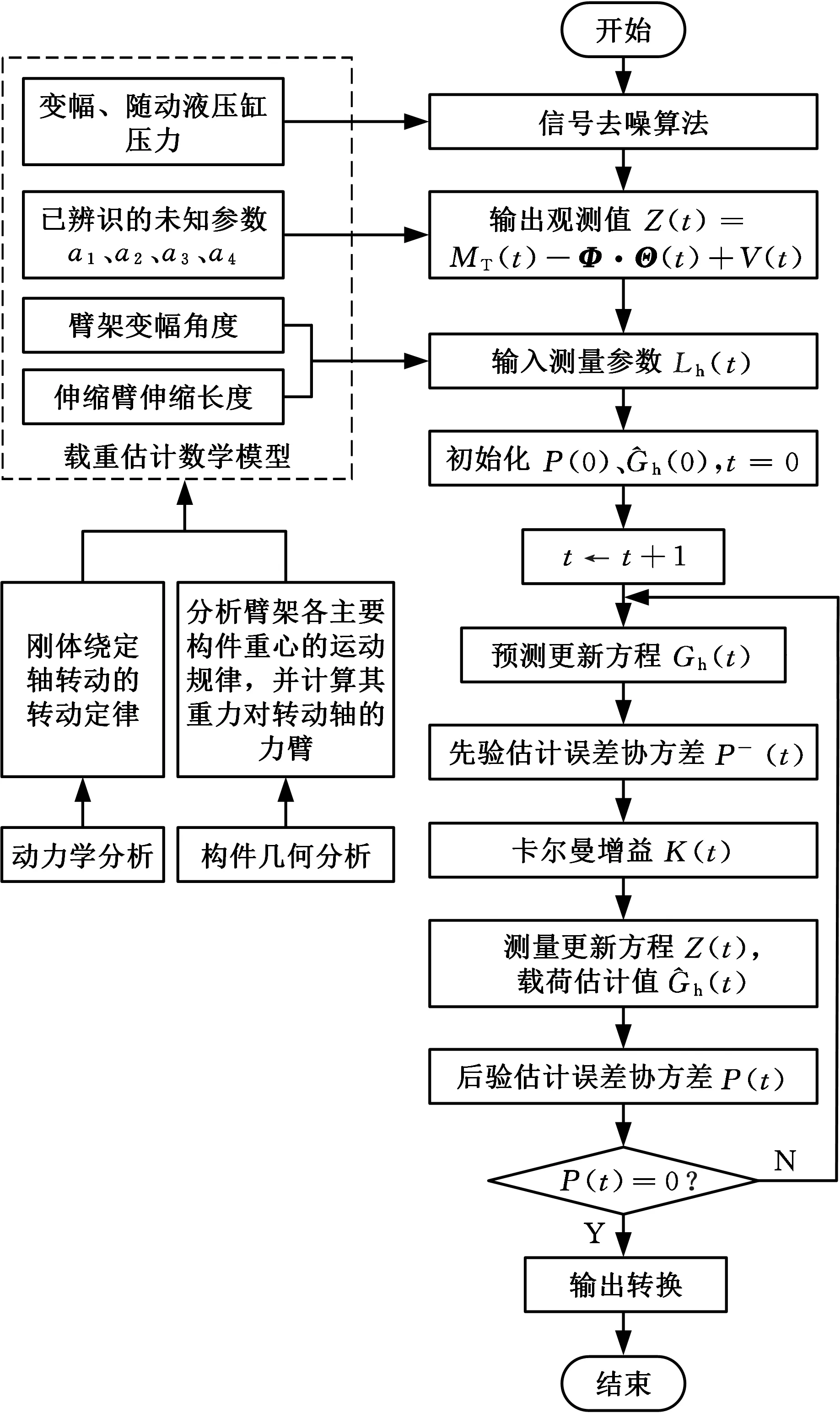
图4 基于卡尔曼滤波的载重估计算法流程Fig.4 Algorithm flow of workload estimation based onKalman filter
在卡尔曼滤波算法辨识递推的过程中,由于后验估计误差协方差P(t)和卡尔曼增益K(t)会迅速衰减到0,并使得大量新测量数据失去对状态变量的校正能力,这种现象称为数据饱和。因此需考虑校正方案,以保持新测量数据对状态变量估计的持续校正能力,进而使载重估计系统能得到准确的估计值。如图5所示的一组数据,在t=100 s时,载重已经发生了很大的改变,但随着P(t)和K(t)快速减小到0,其估计值mh并不能很好地从1500 kg附近迅速地递推到1000 kg附近。
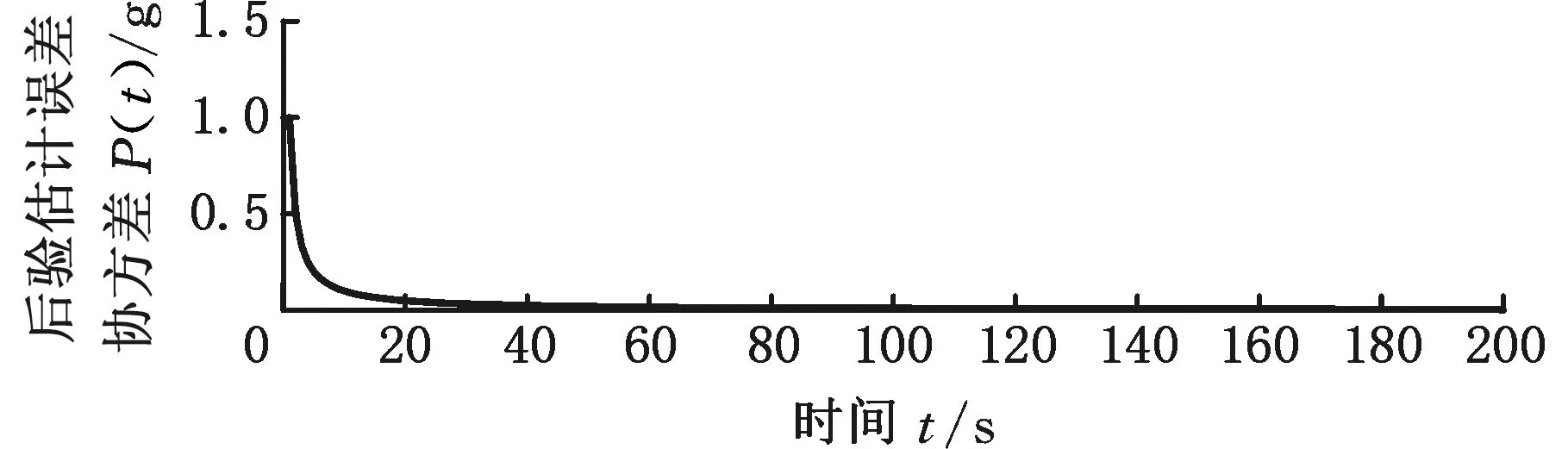
(a)载重质量的后验估计误差协方差
对该现象进一步分析可知,当载重发生改变时,即该估计过程的状态变量已发生了变化,此时的估计过程与状态变量改变前的估计过程已经不是同一过程了,而且此时的后验估计误差协方差也已减小到0,若再延续前一估计过程继续估计,则卡尔曼滤波算法将会无法继续准确递推。
本文受到交互式多模型(interacting multiple model,IMM)[24]的启发,采用两个并行计算的卡尔曼滤波对载重估计数学模型进行辨识递推:第一个卡尔曼滤波主要是起到自适应判断载重是否有较大幅度变化的作用,通过实时监控前后两时刻状态变量之差的更新率,为其设置合适的阈值,进而决定是否重置第二个卡尔曼滤波的后验估计误差协方差,以达到快速响应的效果;第二个卡尔曼滤波主要是起到稳定估计值的效果,其状态变量作为全过程载重估计值的输出。
基于改进卡尔曼滤波的载重估计算法流程如图6所示,具体过程如下。
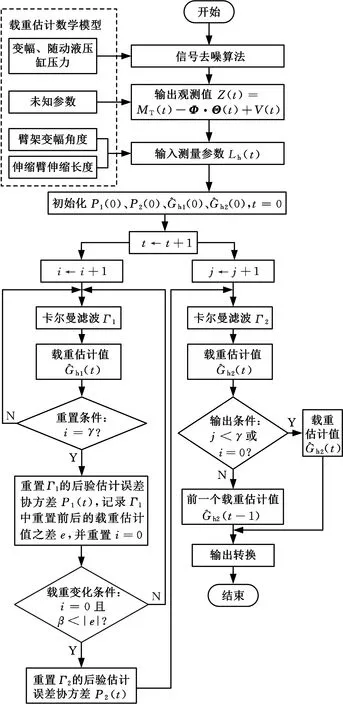
图6 基于改进卡尔曼滤波的载重估计算法流程Fig.6 Workflow of workload estimation algorithmbased on improved Kalman filter
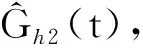
后验估计误差协方差P1(t)和P2(t)重置为初始值的目的是,使大量新测量数据保持对载重估计的校正能力;而采用两个并行计算的卡尔曼滤波进行递推的方式能够起到自适应估计的作用,快速辨识出载重发生变化的时间点,并准确估计出变化前后的载重。
3 载重估计试验验证
3.1 试验平台搭建
试验平台以某企业研发的超长重载伸缩臂叉车为研究对象,具体的基础配置、尺寸参数和性能参数已在前文给出。为了减小各类型传感器测量误差对载重估计准确度的影响,保证其采集信号数据的测量精度,试验采用的传感器包括:Gefran公司GSF系列的位移传感器,长沙湾流智能科技有限公司的VALUER SpaceVector高动态空间角度传感器,Danfoss公司MBS3000型号的压力传感器。传感器的安装位置如图7所示。

(a)角度传感器 (b)位移传感器 (c)随动液压缸 (d)变幅液压缸图7 传感器的安装位置Fig.7 Installation position of sensor
如图7a中白实线圈所示,在第四级臂的头部安装高性能角度传感器,用于实时测量臂架变幅角度。如图7b中白实线圈所示,在基本臂安装拉绳式位移传感器,导线挂在第二级臂,当伸缩臂进行伸缩动作时,实时测量伸缩臂伸缩长度。图7c所示为随动液压缸;图7d所示为变幅液压缸,其中白实线圈内为变幅液压缸无杆腔压力测点,白虚线圈内为变幅液压缸有杆腔压力测点,在测点处安装压力传感器,则可以测量变幅液压缸四个腔的压力。
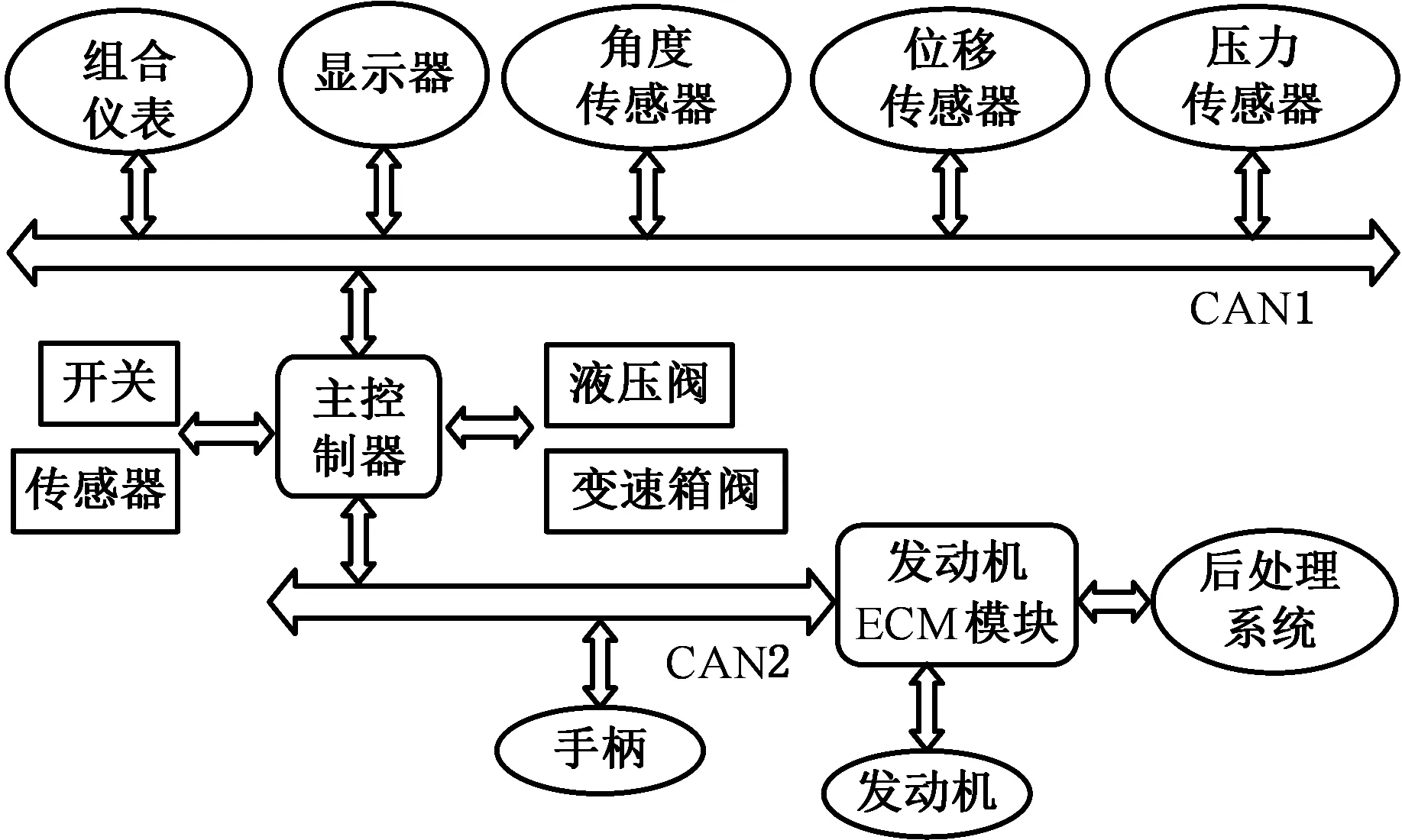
图8 电气系统的主要控制架构Fig.8 Main control architecture of electrical system
伸缩臂叉车电气系统的主要控制架构如图8所示。可以看出,位移传感器和角度传感器以及与采集电路板检测装置的压力信号输入端连接的四个压力传感器通过CAN总线将这六个传感器的模拟量数据发送到主控制器;然后,由主控制器读取传感器输出得模拟量数据并转换成数字量,再将其发送到CAN总线;最后,由主控制器中的载重估计算法模块进行运算处理,最后再将估计结果发送到CAN总线,且由显示器接收并显示。
在试验平台的搭建过程中,为了能够充分满足应变、位移和压力等不同类型信号数据的输入要求,这里使用HBM公司的SoMat eDAQ数据采集系统进行数据采集与分析。将压力传感器连接到臂架系统的液压油路,从总线中接出电信号的采集数据,将压力传感器输出线接入与计算机直接连接的数据采集仪,即可将信号数据输出至计算机中,然后使用SoMat TCE软件进行信号数据采集,试验时的采集频率设置为40 Hz。数据采集仪与计算机直接连接如图9所示。
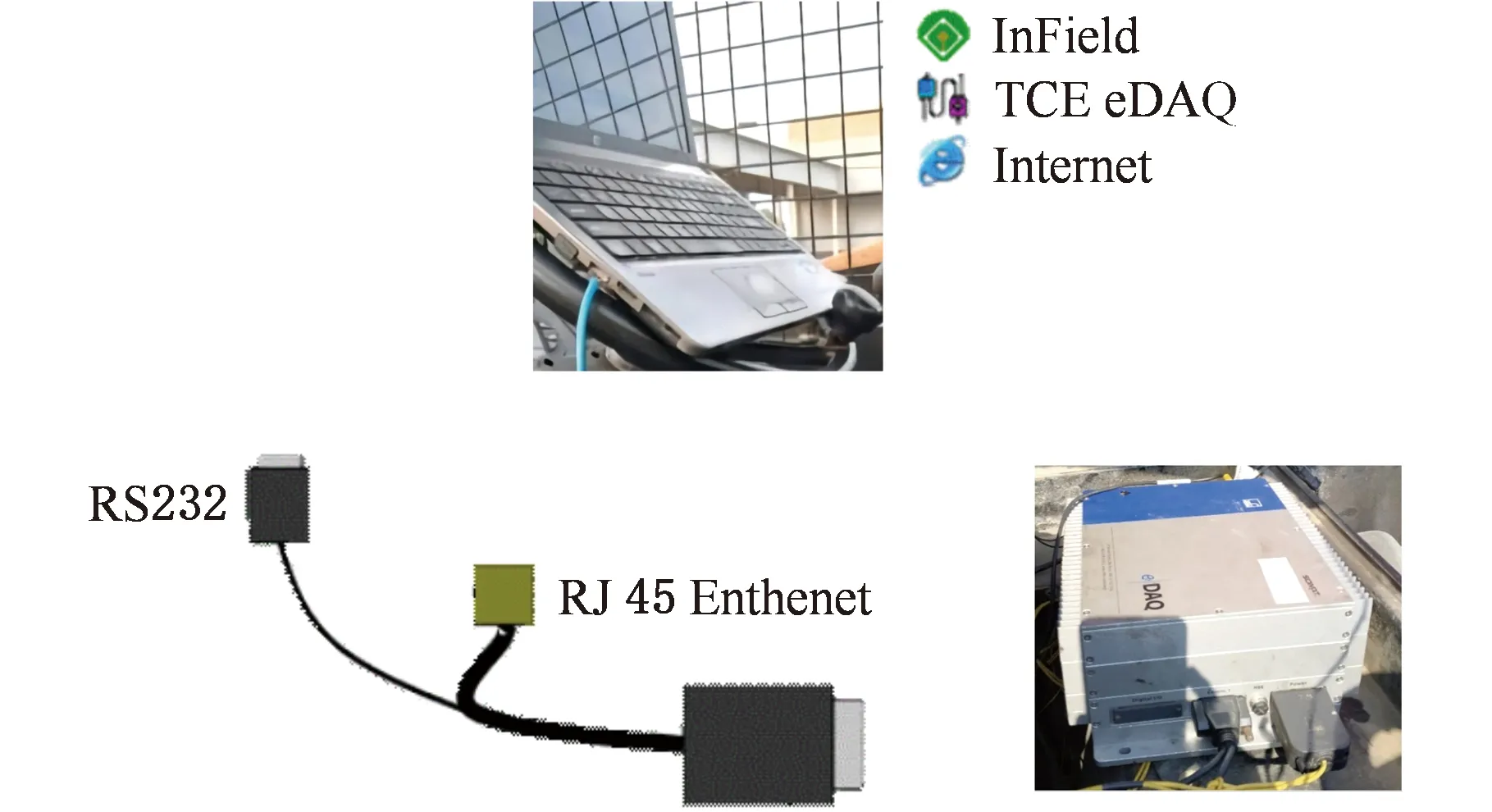
图9 Somat eDAQ数据采集仪与计算机直接连接Fig.9 Somat EDAQ data acquisition instrument isdirectly connected with the computer
3.2 算法初值选择和参数设置
算法中参数的说明与设置如下:
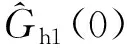
(2)后验估计误差协方差初始值。由式(10)可知,在测量误差协方差R确定的情况下,卡尔曼增益K(t)与先验估计误差协方差P-(t)正相关;而由式(8)可知,在过程误差协方差Q确定的情况下,P-(t)又与后验估计误差协方差P(t)成正比的关系。故P(t)的初值越大,就会使递推过程中计算的K(t)就越大,则意味着实际测量值Z(t)更可信。在该载重估计系统中,由于液压系统压力的测量噪声是很大的,故后验估计误差协方差的初始值P1(0)、P2(0)都设置为100。
(3)测量误差协方差初始值。由预测更新方程和测量更新方程可知,载重估计系统某一时刻的载重值会有两个,分别为经验的预测值和模型的测量值,而卡尔曼滤波算法需要在预测值和测量值之间的过渡阶段,结合过程噪声W(t)和测量误差V(t),递推出该系统在统计意义下最为接近载重真实值的最优估计值,因此在递推过程中到达稳定估计值之前会具有一个过渡阶段。而测量误差协方差R则会影响该过渡阶段所需要的时间以及载重估计值与真实值之间的近似程度。当R比较小时,意味着实际测量值Z(t)越来越可信,而估计测量值Lh(t)Gh(t)则越来越不可信,此时算法收敛至稳定估计值的响应时间很短,但当R过小时,系统容易出现震荡现象;当R比较大时,意味着Z(t)的可信度越来越低,而Lh(t)Gh(t)则越来越可信,此时算法收敛速度很慢,系统的响应时间较长[25]。在实际应用中,可以采集一些离线样本信号,并对其测量信号的噪声,通过分析纯噪声来对R进行确定。通过多次试验的参数调整,卡尔曼滤波Γ1和Γ2的R取0.01~1.00。
(4)过程误差协方差初始值。过程误差协方差Q表示建立的预测模型本身带来的噪声,该参数被用来表示状态转换参数A与实际过程之间的误差。Q会影响辨识递推后曲线的平滑程度,因为无法直接观察系统的估计过程,所以确定其大小是比较困难的。由于在该载重估计过程中默认前后两个时刻的载重是不发生改变的,故卡尔曼滤波Γ1和Γ2的Q都取0[26]。
(5)若卡尔曼滤波Γ1中的阈值γ过小,则会影响系统估计值的不稳定性;若γ过大,则会延长估计系统的响应时间。故γ一般取一到两个采样周期,这里取40~80个采样点。阈值β表示为判断载重发生变化的幅度,变化幅度一旦超过阈值就会触发后验估计误差协方差P2(t)重置为初始值,这时估计过程将重新开始。阈值β根据试验时的经验值,取200~500 kg。
3.3 离线试验结果与分析
进行了四组不同载重的离线试验,验证所提出的基于改进卡尔曼滤波的载重估计算法是否达到以下产品研发要求:
(1)对于454 kg的轻载荷,其估计结果的最大绝对误差应小于91 kg。因为该载重估计数学模型主要利用液压系统压力信号实现间接估计,轻载对液压缸压力变化的敏感度较小,伸缩臂叉车臂架的稳定性较差,从而会导致估计难度陡增,所以在轻载情况下,估计精度可以适当地降低。
(2)对于2268 kg、3368 kg和4536 kg的重载荷,其估计结果的平均绝对百分比误差应小于3%。
(3)在臂架变幅和伸缩臂伸缩等多任务况造成较大的冲击时,算法依然能够快速收敛到真实值,即算法需要满足载重估计的稳定性。
离线试验的结果如图10~图13所示,其中伸缩臂长度l为基本臂与3倍伸缩臂伸缩长度Δl之和。离线试验是在MATLAB2019a环境下进行的,计算机处理器为英特尔第三代酷睿i5-3320M 2.60 GHz,运行内存为海力士8GB DDR3L 1600 MHz。
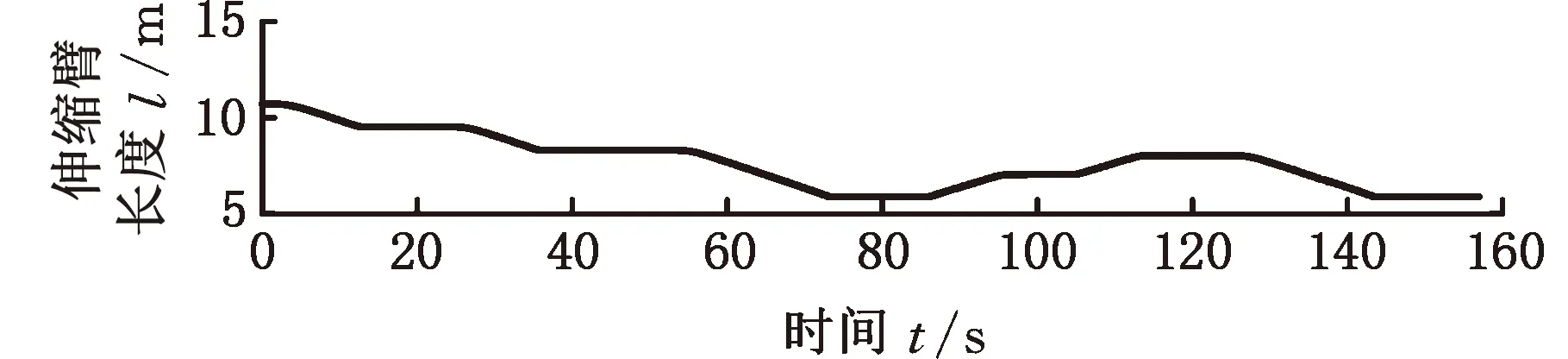
(a)伸缩臂长度
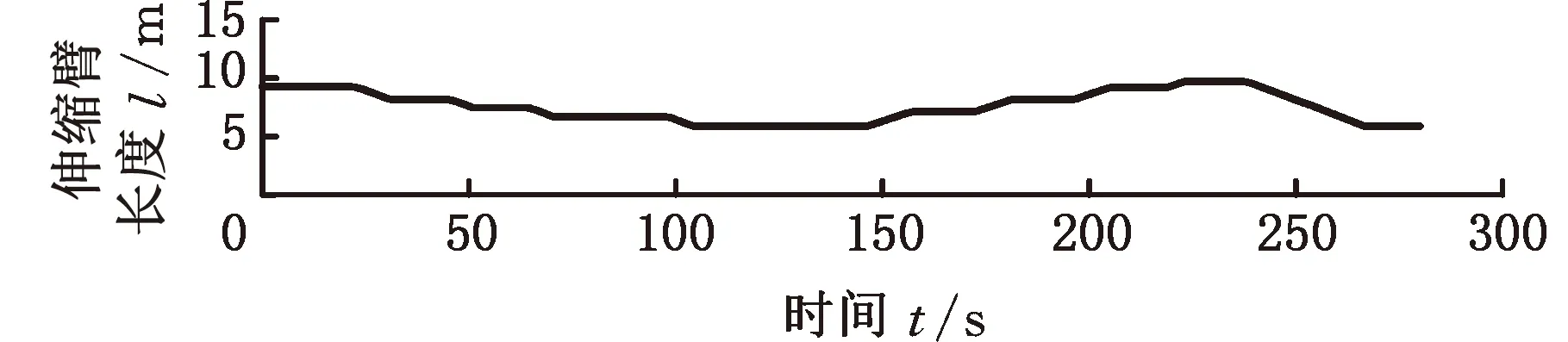
(a)伸缩臂长度
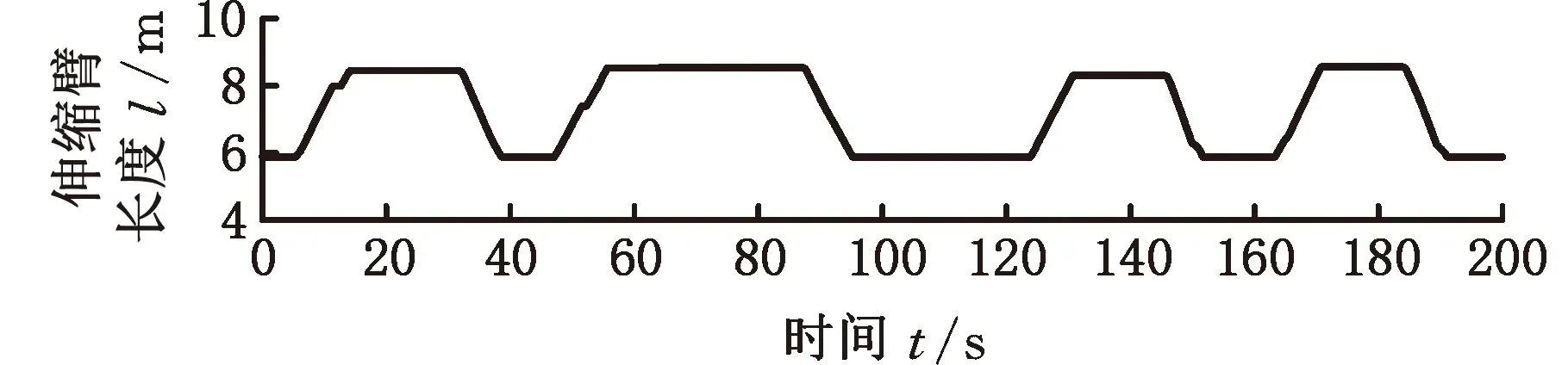
(a)伸缩臂长度
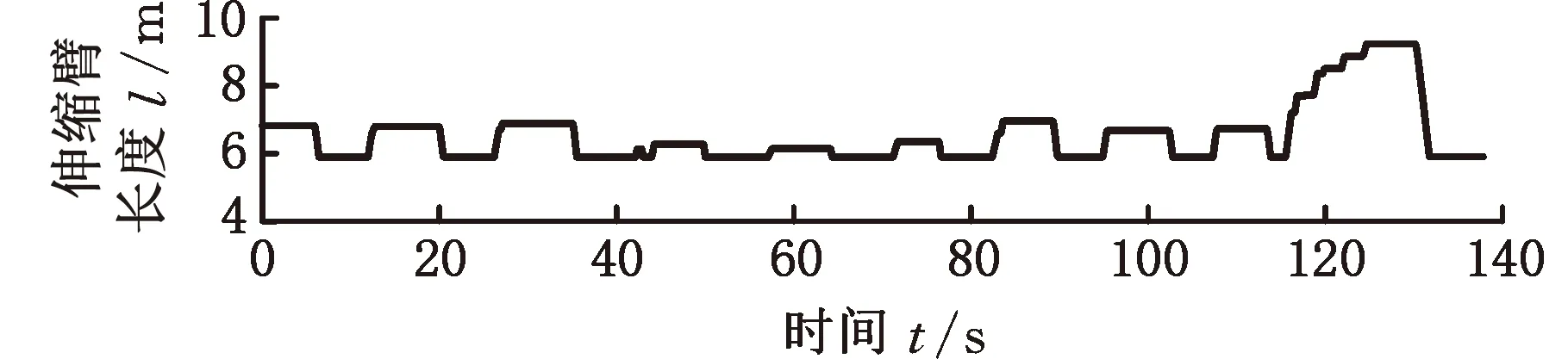
(a)伸缩臂长度
分析图10~图13的臂架变幅和伸缩臂伸缩过程可以发现,当进行变幅和伸缩动作时,会造成液压系统压力振荡等不稳定性情况,在未使用载重估计算法辨识递推而根据载重计算公式直接求解时,载重会有相当大的波动,严重偏离了真实值;而使用载重估计算法辨识递推之后,载重估计值可以快速收敛至真实值。辨识递推前后的载重质量见表2。
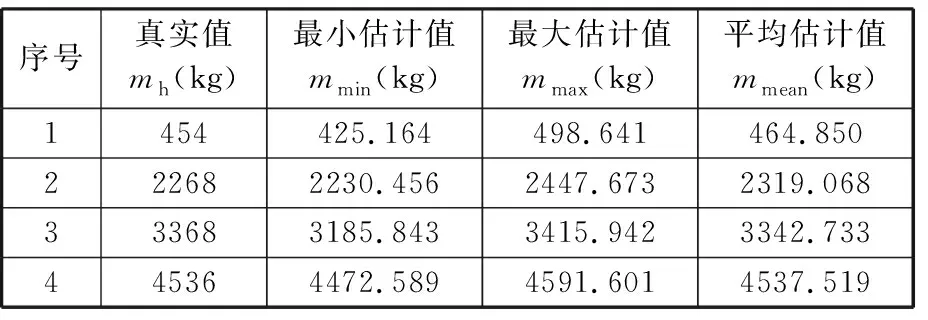
表2 辨识递推前后的载重质量(离线试验)
使用最大绝对百分比误差emax和平均绝对百分比误差emape以及其辨识递推过程所需的计算处理时间对所提出的基于改进卡尔曼滤波的载重估计算法进行定性和定量评价。emape表示估计值较真实值的平均偏离程度,其值越小,说明载重估计模型准确度越高。辨识递推后的载重绝对百分比误差及计算时间见表3。
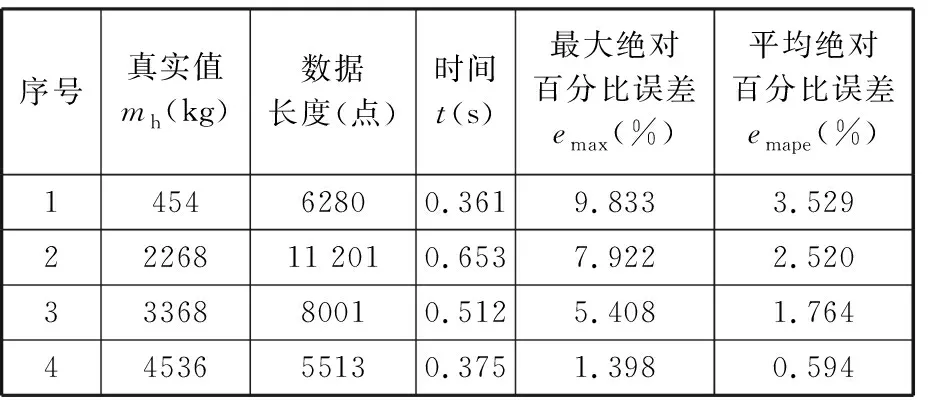
表3 辨识递推后的载重绝对百分比误差及计算时间
由表3可以看出,经过载重估计算法快速准确辨识递推之后,除了第1组454 kg的载重试验外,第2~4组试验的平均绝对百分比误差都在3%以内;再结合图10~图13来看,最大绝对百分比误差都是在臂架变幅上升的初始阶段或变幅角度最大的位置(红实圈处),因为在这些位置上,伸缩臂处于变幅的极限位置或者叉具触碰地面等情况,导致整个臂架受力比较复杂;对于454 kg的载重试验,其平均绝对百分比误差和最大绝对百分比误差都比较大,但其最大绝对百分比误差9.833%在要求的范围内;从辨识递推时间来看,基于改进卡尔曼滤波的载重估计算法的计算效率比较高。根据离线试验的分析结果,初步达到了试验的目的与研发的要求。
3.4 在线试验结果与分析
最终的在线试验结果如图14~图18所示。对图14~图18中伸缩臂叉车带载重时臂架变幅和伸缩臂伸缩过程分析可知:
(1)对比辨识递推前后的载重质量,使用基于改进卡尔曼滤波的载重估计算法求解该数学模型,估计结果的稳定性得到了很大改善,即使辨识递推前载重会有相当大的波动,辨识递推后也可以快速收敛至载重估计值真实值附近;
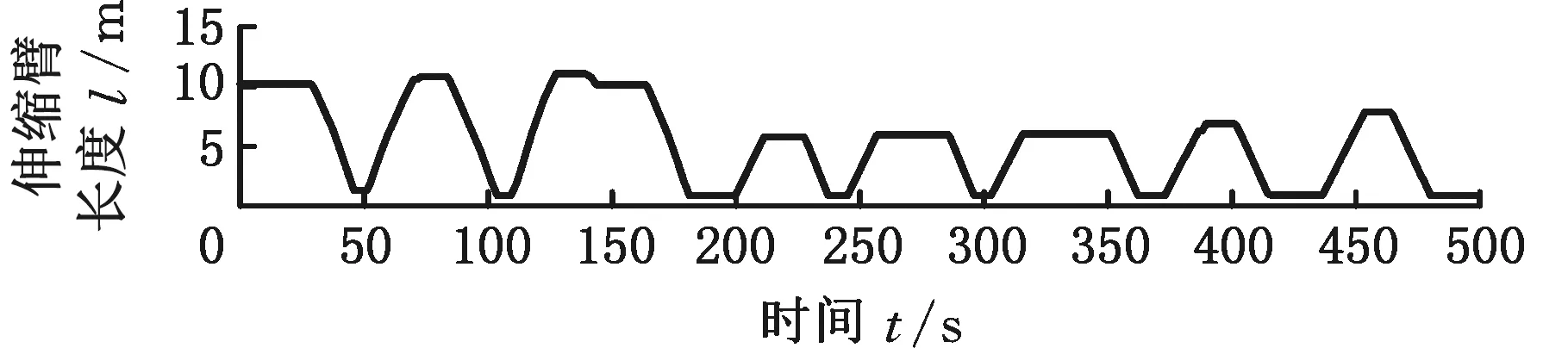
(a)伸缩臂长度
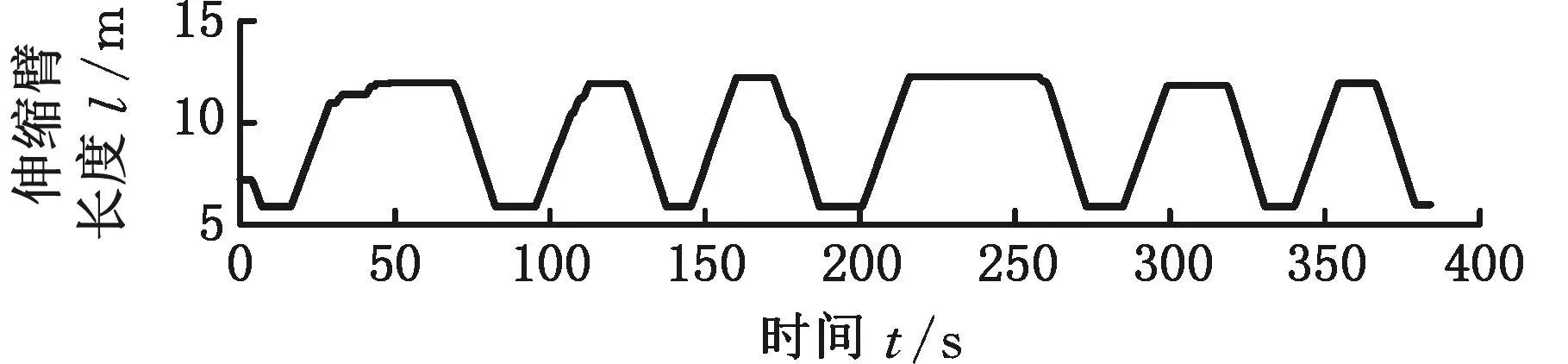
(a)伸缩臂长度
(2)当要叉起一个置于地面的货物时,由于提升前货叉是处于松弛状态,而伸缩臂叉车以较快的速度突然变幅提升载重,这样的起升过程会产生一个较大的惯性冲击,从而导致载重估计值偏离真实值(红实线圈处)。所以为了提高载重估计的准确度,在作业现场,操作员应当以较低的速度叉起重物,进而使臂架逐渐受力及变形后,再以额定速度变幅提升;
(3)当臂架变幅角度达到最大角度71°或者变幅角度为0°时,整车的稳定性能最差,载重估计值会产生较大的波动(红虚线圈处)。这是由于液压系统的泄压、保压和漏油等原因造成的。
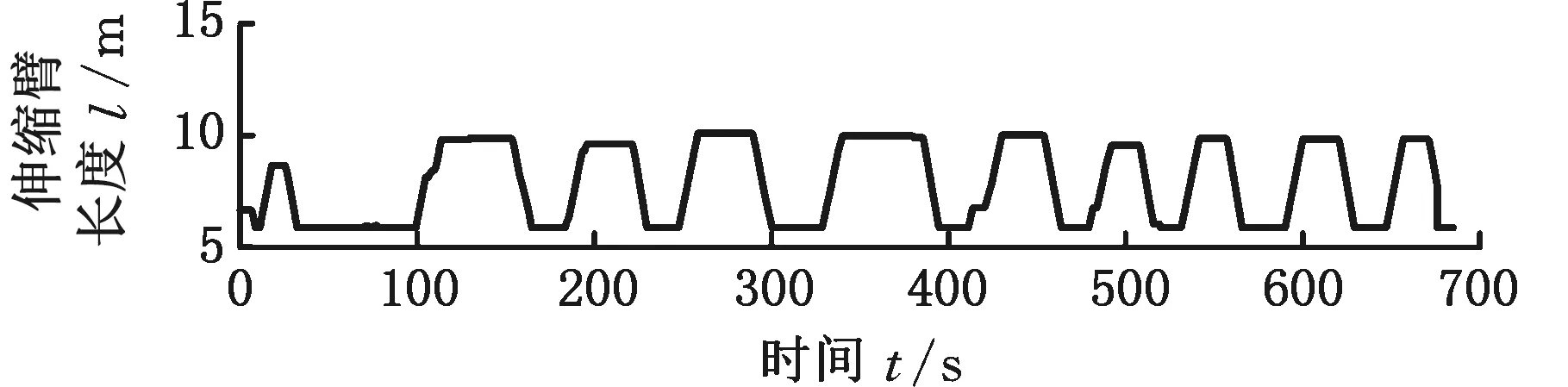
(a)伸缩臂长度
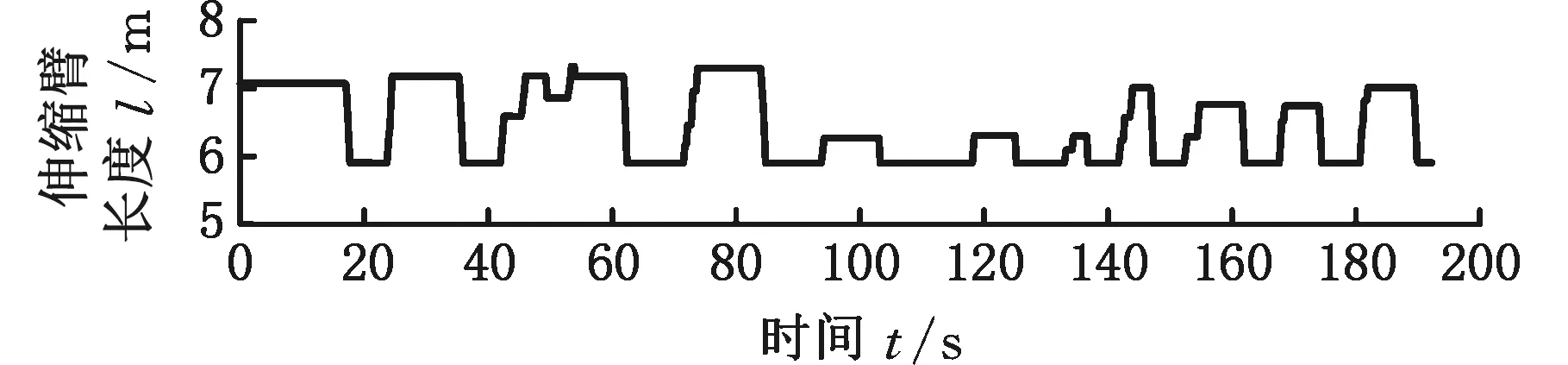
(a)伸缩臂长度
以上5组不同载重的在线试验,其辨识递推前后的载重质量见表4。辨识递推后的载重绝对百分比误差见表5。
由表5可以看出,经过载重估计算法快速准确辨识递推之后,除了第5组454 kg的载重试验外,第6~9组试验的平均绝对百分比误差都在3%以内;与离线试验相同,最大绝对百分比误差也都是伸缩臂处于变幅范围的极限位置或在变幅提升的初始阶段;对于第5组454 kg的载重试验,其平均绝对百分比误差和最大绝对百分比误差也比较大,其最大绝对百分比误差16.142%,但也在要求的范围内。
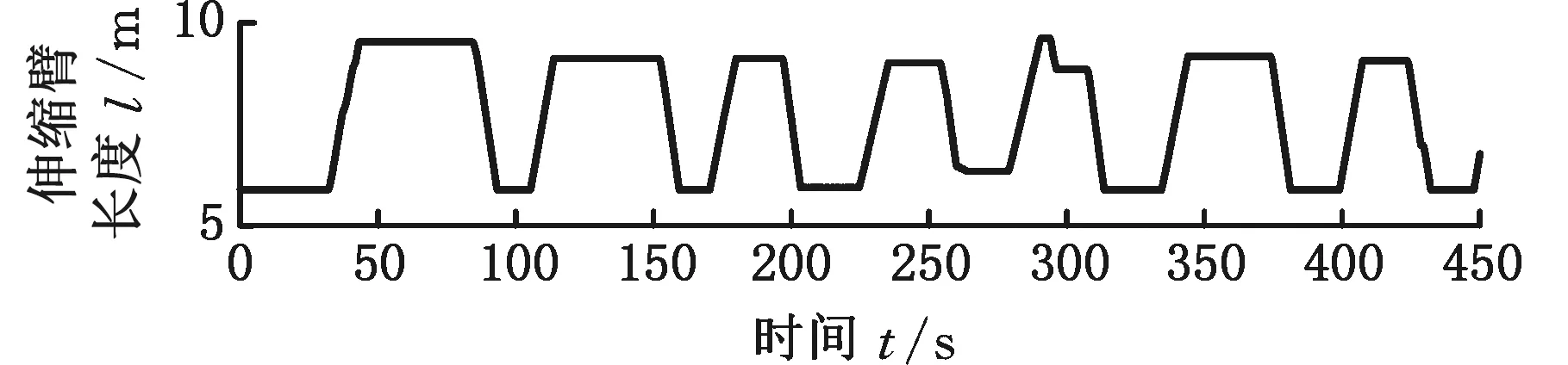
(a)伸缩臂长度
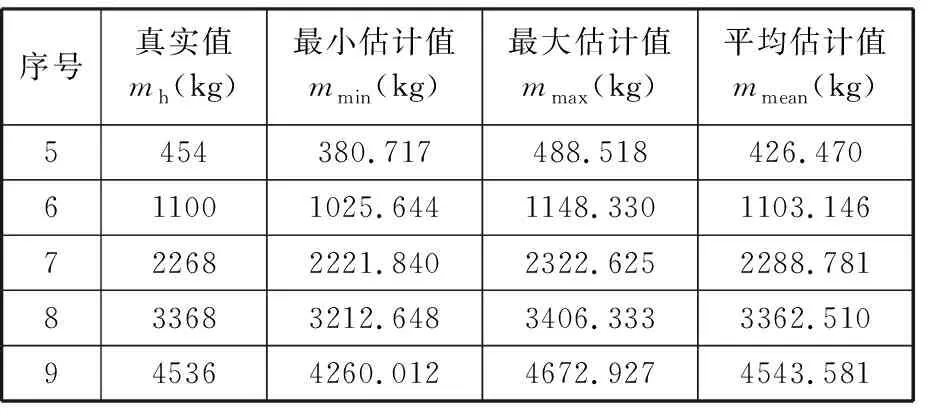
表4 辨识递推前后的载重质量(在线试验)
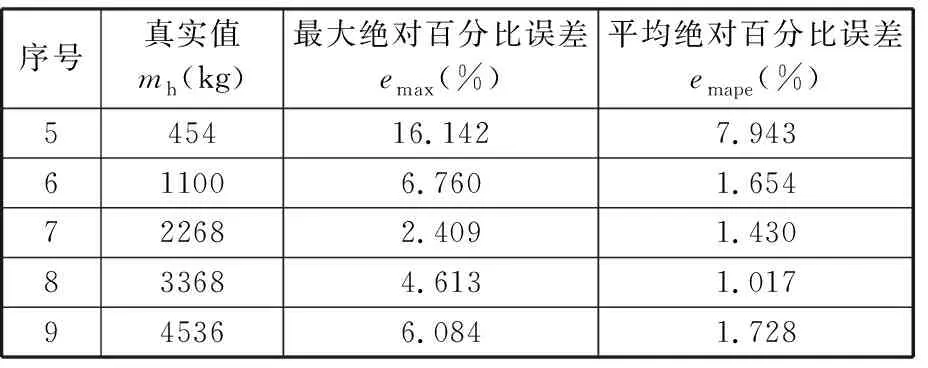
表5 辨识递推前后载重估计的绝对百分比误差
为验证本文所提出的载重估计算法解决数据饱和现象的性能表现,以及更换载重或载重发生较大幅度变化时,该算法能否快速收敛到相应载重的真实值,即载重估计系统达到稳定估计值的响应时间是否很短,进行了更换不同载重的在线试验。伸缩臂叉车载重发生变化时的在线试验如图19所示。
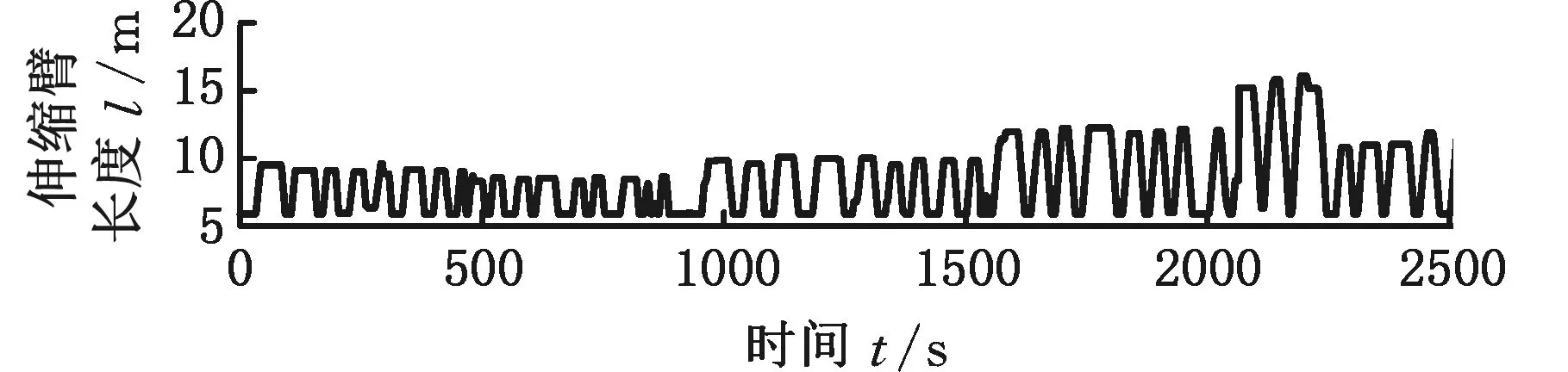
(a)伸缩臂长度
与图5相比,由图19可以看出,每当载重发生变化时,该系统不仅能够自适应估计,而且能够快速准确地辨识递推到相应载重的真实值附近,趋于稳定估计值的响应时间可以在1 s之内。
4 结语
本文在伸缩臂叉车工作装置的结构组成和工作原理的基础上,建立了基于动力学的载重估计数学模型,并推导出了载重计算公式,然后将该公式作为卡尔曼滤波算法的测量更新方程,将载重估值作为预测更新方程的状态变量,对数学模型进行求解。最后,通过不同载重的离线试验和在线试验,得出以下结论:
(1)将载重估计作为一个模型辨识和参数估计的问题来处理,即根据动力学原理和伸缩臂叉车工作装置的几何结构关系,推导出一个含有未知参数的数学模型,然后用基于卡尔曼滤波算法递推辨识载重的估计值,此种通过液压缸压力值间接估计载重的方法具有可行性和可靠性。对于454 kg的轻载荷,其估计结果的最大绝对误差小于91 kg,而对于1100 kg、2268 kg、3368 kg和4536 kg的重载荷,其平均绝对百分比误差小于3%,而且估计系统稳定性好。该估计方法模型简单、可移植强,可以扩展应用到吊车、门座起重机等工程机械的载重估计领域,对工业领域的自动化、智能化具有一定的实际应用意义。
(2)经过在线试验验证,本文所提出的基于改进卡尔曼滤波的载重估计算法能够解决因载重发生突变以及大量新测量数据失去而对载重估值进行校正的数据饱和问题。当载重发生变化时,该算法能够自适应且快速准确地辨识递推到相应载重的真实值附近,趋于稳定估计值的时间可以在1 s内。
本文针对伸缩臂叉车工作载荷快速准确估计方法进行了初步的理论分析和试验验证,但由于研究内容涉及的范围较为广泛,对影响该方法的一些其他因素和情况未能进行更加详细和深入的研究。后续可以从以下几个方面进行进一步研究:
(1)在建立基于动力学的数学模型时忽略了液压油温度、摩擦力和工作装置磨损度等因素。不同温度下液压系统液压油黏度等特性会发生变化,从而改变液压缸液压力,但是影响不大,一般可以采用强制预热的方法解决;而摩擦力主要产生于工作装置各个铰接点处,特别是臂架与车架的铰接点,为了减小误差,可以考虑在工作载荷估计数学模型引入补偿系数。这些因素还会影响工作载荷估计数学模型中的四个未知参数,而本文采取的是离线辨识,为了避免需重新辨识参数而造成的麻烦,还需研究在线辨识未知参数的情况。
(2)由离线试验和在线试验的试验结果可知:当进行变幅和伸缩动作或以较高速度突然变幅提升重物时,由于惯性冲击等作用会造成液压系统压力的不稳定,导致工作载荷的绝对百分比误差会比较大;在初始阶段或变幅角度最大处时,由于伸缩臂处于变幅的极限位置或者叉具触碰地面等情况,导致臂架受力比较复杂,通过工作载荷估计算法辨识递推得到的工作载荷估计值也会有相当大的波动。为此,可以在伸缩臂上安装霍尔传感器,在设定的变幅角度和伸缩长度条件下,自动采集液压缸压力数据,选择数据中的某一区间作为估计系统的有效数据采样区间,进而进一步提高估计的准确度。
