基于密度聚类和圆外切线斜率拟合的埋地排水管道声呐点云去噪技术

吴俊豪，李 琛，王 蓉，刘文黎，周星宇

(华中科技大学 土木工程与力学学院，湖北 武汉 430074)

1 前 言

排水管道作为城市的生命线工程，关系着城市防涝[1]、水体黑臭整治[2]、城市水循环[3]等重要领域的健康安全运转。然而，目前由于管道的阶段化建设，周边施工诱发管道迁移，管道老化、破损、变形等病害的影响，导致管道信息不全面、不完备、不准确，从而给管网的运维管理带来不便。因此，如何准确高效地探明城市既有地下排水管网情况，对城市的管网维护有着重大意义。当前，排水管网的现代检测方式有CCTV检测[4]、探地雷达检测[5]、激光检测[6]、声呐检测[7]等。其中，声呐检测[8]因为可以实现水下检测和高稳定性的特点，在城市排水管道探测中得到了广泛应用。但是，由于检测设备自身振动、管道内水流混声等因素的影响，在管道检测中利用声呐技术生成的点云数据中往往会不可避免地存在噪声点，如何高效精确地去除这些噪声点，是利用声呐技术进行管道检测面临的一大难点。

国内外学者一直关注点云去噪技术的发展，如Ester等提出了基于密度的噪音聚类方法[9]，但在进行聚类优化时，需要主观输入部分关键变量；2014年，Rodriguez A和Laio A在《Science》上提出聚类中心的特征是密度高于其临近代理值，并且与密度较高的点的距离相对较大[10]；张玉存等提出基于曲率约束的点云分割去噪方法，通过曲率约束来保持模型特征[11]；程一峰和刘增力采用稀疏贝叶斯学习对图像信号进行预处理，结合Bartlett检验法裁剪掉噪声原子[12]；章曼等提出了一种基于自适应可达距离的密度峰值聚类算法(ARD-DPC)，利用非参数核密度估计方法计算点局部密度，避免了截断距离的主观选取[13]。总体来说，目前的研究主要聚焦于从数理方面改进噪声聚类优化算法，缺少结合实际工程背景和声呐点云特点，给出适用于特定领域，如聚焦城市排水管道的点云去噪聚类优化方法等方面的研究。

为了更精准地去除基于声呐技术生成的排水管道点云模型中的噪声点，同时有效保留管道内壁和淤积线的点云特征，本文提出将密度聚类优化算法(density clustering optimization algorithm, DBSCAN)和类圆外切线斜率拟合相结合的方式进行点云去噪。首先针对管壁环状的特征，确定合适的全局邻域半径和Min Pts个数，通过密度聚类优化算法识别核心对象和密度相连点，有效排除噪声对象，得到去噪后的管道内壁扫描点和淤泥扫描点；其次，在处理后的点云数据基础上，采用类圆外切线斜率拟合的方式，提高管道内部特征点云数据拟合的效率和识别精度，得到精确的管道内壁和淤积淤泥拟合曲线；最后以武汉市某排水管道为工程案例，分析了DBSCAN密度算法和斜率拟合方法的应用效果。

2 点云去噪和拟合方法

声呐检测过程中，由于排水管道内水流混声和声呐检测设备自身的振动等多因素的影响，导致声呐点云扫描结果噪声严重、边缘恶化，不易识别出管道内壁和淤泥淤积线。因此，为提高声呐扫描数据处理的效率和准确度，首先需要在现有声呐检测技术基础上，通过对扫描点云结果的去噪优化，在保留管道内壁特征同时，去除噪音点，得到优化后的点云数据；其次，通过类圆截面拟合算法，拟合出排水管道的内壁曲线；最后，结合管壁和点云扫描特征，得到淤泥淤积曲线。

2.1 DBSCAN算法

DBSCAN算法作为一种经典密度算法，基于点云密度对数据进行处理，避免了需要人工设定聚类簇的数量，可以在有噪声的数据库中有效识别任意形状的簇。其算法的核心步骤在于寻找核心点，通过将寻找到的相邻核心点连成一片，从而得到所需要的簇。

为理解DBSCAN算法，有几个基本定义[14]：

(1) 邻域(Eps)：指在数据集范围内，以每个数据点为圆心所形成的半径为ε的圆圈区域，对于任意数据点xi落于圆圈范围内，则称xi属于该Eps。

(2) 密度值：落在数据集内任意数据点xi既定半径ε邻域范围内的数据点个数称为该点的密度值。其中，可以人为选定密度阈值(MinPts)作为核心点判别标准，如果数据点xi密度大于等于密度阈值，则判定该点为核心点。

(3) 边缘点：当数据点密度小于密度阈值，但位于核心点邻域范围内时，则称该点为边缘点。

(4) 噪声点：若数据点密度小于密度阈值，且该点不处于任意核心点邻域范围内时，记该点为噪声点。

(5) 直接密度可达：对于核心点x1和任意数据点x2，数据点x2位于核心点x1邻域范围内，则称点x1和点x2直接密度可达。

(6) 密度可达：对于数据集内数据点x1，x2，…，xn，其中n≥2，满足xi到xi+1直接密度可达，则称数据点x1，x2，…，xn密度可达，显然，数据点x1，x2，…，xn-1都必须是核心点。

(7) 密度相连：如果数据集内存在数据点xx到数据点xy和xz都是密度可达的，则称数据点xy和xz密度相连，可以看出，该性质具有对称性，既点xy和xz密度相连等价于点xz和xy密度相连。

DBSCAN算法的详细流程如图1所示。

图1 DBSCAN算法流程Fig.1 DBSCAN algorithm process

在算法的实际应用过程中，通过设定邻域(Eps)和密度阈值(MinPts)，寻找出数据集中的核心点，选定任意核心点xi为起点，通过将直接密度可达的核心点连接起来，同时将边缘点连接至最近的核心点上，直至所有密度相连的点都连接起来，形成所需要的簇，实现聚类，同时识别噪声点。

在性质上，同一个簇内的点必定是密度相连的，且簇内点的任意密度可达点必定属于该簇。

2.2 圆外切线斜率拟合(SFA-COT)算法

由微分定义可知，当平面内两点之间相距距离极近时，斜率与微分近似相等。因此，对于圆截面来说，可以将圆面上点的切线斜率近似等价于该点的微分。

(x-a)2+(y-b)2=r2

(1)

(2)

图2 标准圆面上点切线斜率变化趋势Fig.2 The slope change of the outer tangent of a standard circle

其中，式(1)为圆的标准方程，式(2)为圆的斜率方程，根据圆的切线斜率方程性质可以知道，当设定圆心为原点时，圆上点切线斜率变化与圆的半径无关，且圆斜率呈连续变化趋势，如图2所示。因此，通过计算相临近点云之间的斜率变化趋势是否与圆斜率变化趋势相匹配，可以筛选出位于圆截面上的扫描点云点。

为表述方便，定义正圆面上点与圆心连线和y轴夹角、椭圆面上点与原点连线同y轴夹角统称为圆心偏向角。

由图3可以看出，当为正圆面时，圆上一点A切线的斜率k与圆心偏向角tanθ1数值相等，而根据两条相互平行线之间内错角相等原理，tanθ1的值可由对应两条边的长度比值得到，即有如下等式：

(3)

图3 圆外切线计算原理图Fig.3 The calculation principle of the outer tangent to the circle

针对椭圆面，由于椭圆上一点的切线斜率与该点和原点之间连线斜率乘积为定值，即：

(4)

(5)

其中，式(4)为椭圆标准方程，式(5)为椭圆面上一点的切线斜率与该点和原点之间连线斜率的乘积定值计算公式，显然椭圆上一点的切线斜率与该点和原点之间连线斜率成反比例关系，即与圆心偏向角斜率呈线性关系。当需要拟合的截面为椭圆时，同一象限内相邻点云点的斜率变化仅与椭圆长短轴相关，具有连续变化趋势。在实际应用中，通过迭代确定椭圆长短轴长度范围，可以得到较好的拟合效果。

结合图2和图3可知，当以x轴为起始线逆时针选点进行斜率计算时，位于圆面上的点云点之间斜率变化趋势符合tanθ曲线。在实际应用场景中，虽然不能确定管道圆心的坐标，但通过选取点云的均值中心点作为假设圆心O1，其第一和第二象限上的逆时针相邻点云点间斜率仍呈单调递增趋势。选定假设圆心，计算固定角度θ范围内点云之间的最小斜率，minkθn>minkθ2>minkθ1>tanθi，通过增大θi的值，最终能筛选出合适的拟合圆截面。

当然，为减少计算量，根据圆切线斜率连续变化性质，且圆上相邻两点之间的欧氏距离必定最小，可以选择位于同一邻域内的直接密度可达点之间进行斜率计算。在已知两点坐标的情况下，通过代入斜率计算公式，算出两点之间的斜率，再代入圆切线斜率变化方程进行迭代计算。图4为圆外切线斜率拟合流程图。

图4 圆外切线斜率拟合流程图Fig.4 The process of fitting the slope of the tangent to the circle

3 DBSCAN算法应用和拟合流程

本文研究对象为排水管道，其标准制式为圆柱体，因此，对排水管道内壁进行拟合时需要得到的聚类簇可以视作圆面。

根据最小二乘法和中垂线定理推论可知，至少3点能够确定一个圆面，当圆面上的确定点越多，拟合效果越好。为保证排水管道内壁的拟合效果，需要尽可能准确地找到位于管道内壁同一截面上的点。因此，通过采用DBSCAN密度算法，对声呐扫描得到的点云数据进行聚类优化，去除原始点云数据中的噪声点。之后，在去噪处理初筛后的数据基础上，利用圆面外切线斜率拟合的方式，尽可能找出更多圆面上的点，得出最终的类圆拟合曲线。此外，由于管道内部存在淤泥，在实际数据处理过程中还需要识别出淤积线。

DBSCAN算法在计算过程中需要自主设定邻域半径和密度阈值(MinPts)。为得到最优的计算结果，通过计算数据点之间的欧式距离，由大到小排序并绘制曲线，选择曲线上临近中段部分梯度最大点的欧式距离作为邻域半径。因为由梯度定义可知，该点两侧的点云欧式距离变化幅度最大，选定该点数值能兼顾去噪效率和精确度。在确定了邻域半径的基础上，试运行程序得到每个数据点的密度值，将全部密度值的算术平均值作为密度阈值(MinPts)。

(6)

Pi为数据点i的密度值。在数据去噪结果基础上，通过圆外切线斜率拟合方式，确定排水管道内壁截面上的点，之后，通过类圆曲线进行光顺处理。

具体流程如下：(1) 多次试验确定密度算法的邻域半径和密度阈值(MinPts)；(2) 基于密度算法，去除截面点云数据中的噪声点，得到排水管道内壁数据核心点和淤积曲线数据核心点；(3) 通过圆外切线斜率拟合算法，在全部核心点的基础上识别出管道壁上的核心点；(4) 设定半径线性变化的圆截面去网罗数据点，所包含数据点最多的圆面即为最终拟合管道内壁；(5) 在得到排水管道内壁截面的基础上，针对DBSCAN算法所发现的非噪声点，其中单独聚类且斜率变化相对平缓的数据集点即为拟合出来的淤积线。

4 实验结果与分析

为验证算法的实用性，本文以武汉市某排水管道为工程案例，进行实地探测。由于本文主要探究声呐点云去噪和排水管道内部情况截面拟合问题，管道本身的连接性质并非显著影响因素，为简化实地检测过程，故选取直线布置的城市支干管道作为试验场地，相邻管道的设计直径保持一致。

管道的空间布局和井口布置如图5所示，在实地测量过程，通过搭载有HLD-S1型号声呐机器人进行管道扫描，共得到98万个点云数据。

图5 武汉市某排水管道布置示意图Fig.5 Schematic diagram of a drainage pipeline layout in Wuhan

图6(a)为其中一个截面声呐扫描点的原始数据二维呈现。可以看出，初始扫描点云图除了管道壁和淤积线以外，还存在有大量噪音点，影响管道内壁和淤积线的最终拟合效果。

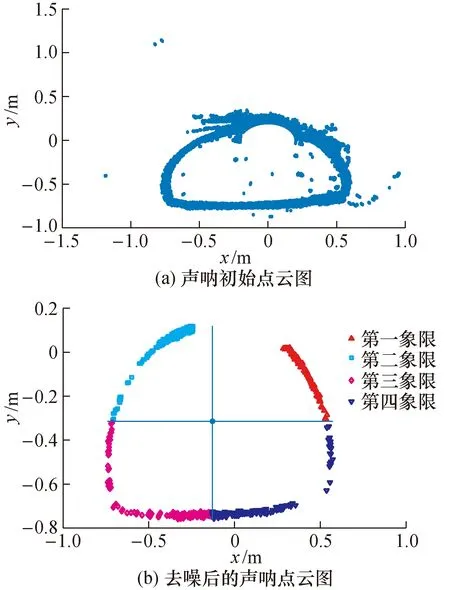
图6 声呐扫描点截面数据Fig.6 Sectional data of sonar scanning points

由于噪声的发生具有瞬时性[15]，有理由相信，当多次扫描同一截面时，反复出现的信号点即为管壁点或者淤积点。所以，为减少数据处理量，通过声呐自带的信号值强度检测，可以初步筛选出描述管道内部特征的点云点。

将初筛后的声呐扫描点二维坐标数据代入设定好初始邻域半径(ε0=0.04)和密度阈值(MinPts0=10)的DBSCAN算法，可以有效识别出点云中密度值符合要求的核心点，删除掉噪声点后，根据剩余全部点云点的均值中心点划分出4个象限的排水管道内壁和淤泥点云二维呈现如图6(b)所示。

根据圆外切线斜率拟合算法，固定角度为10°，可以将全部点云数据划分为36个部分，如图7(a)，其中每个部分范围内求取临近角度两两核心点之间的斜率，可以得到范围内核心点的斜率值。

根据计算得到的斜率结果，以对应角度作为横坐标，斜率取值作为纵坐标，可以绘制出每个核心点在坐标轴范围内的空间位置，通过与标准圆的斜率变化进行比较，可以筛选出位于圆面上的点。由于存在斜率值过大的离散核心点，为更好地比较效果，图7(b)将y轴值范围限制在[-20,20]之间。

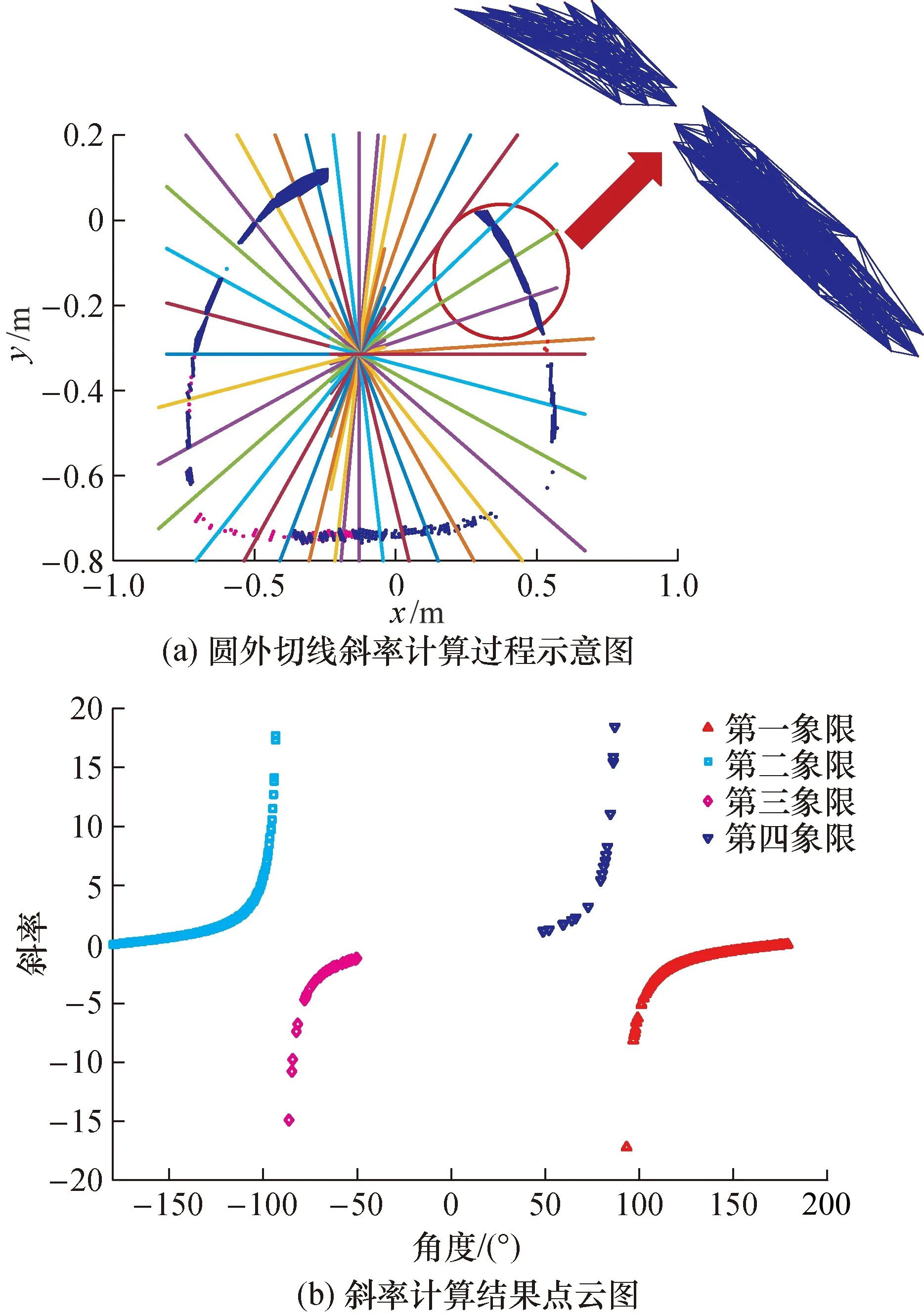
图7 斜率拟合算法过程示意图Fig.7 Schematic diagram of the slope fitting algorithm process

结合圆外切线斜率拟合原理筛选后得到的圆面上核心点，用圆的极坐标方程去拟合相关点，根据最小二乘法原理，圆方程需满足尽可能多的核心点位于圆面上。如图8，通过迭代计算得出圆极坐标相关参数值，从而绘制出拟合圆截面，

x=x0+ρcosθ

(7)

y=y0+ρsinθ

(8)

图8 排水管道壁拟合示意图Fig.8 Fitting diagram of the inner wall

图9为光顺处理过后的最终结果，从图中可以明显看出管道内壁轮廓和淤泥的淤积曲线，相较于图6(a)，已经完全处理了声呐扫描过程中形成的噪音点，并且通过圆外切线斜率拟合的形式，在保留原始扫描管道内壁特征的同时，得到了管道的内壁截面和淤积曲线图，验证了文中方法的实用性。

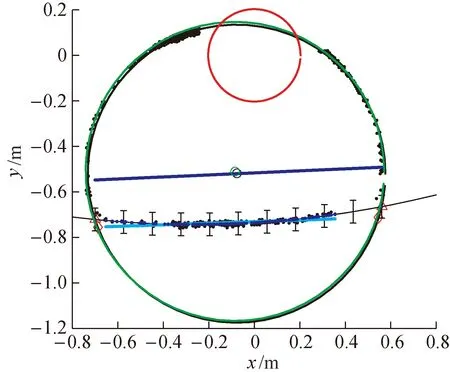
图9 管道内壁和淤积拟合曲线Fig.9 Fitting curve of pipeline inner wall and siltation

为验证文中方法的精度可靠性，需要对拟合圆心C和半径R进行估计[16]。由于管道空间位置的不变性，本文仅就半径拟合值进行对比分析。通过对比另外3种常见聚类算法聚类得到的半径拟合结果，如表1所示。

表1 常见聚类算法聚类结果指标对比Tab.1 Comparison of common clustering algorithm result indicators m

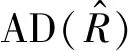
(9)

(10)

(11)

(12)

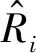
5 结 论

本文以武汉市某排水管道为例进行分析，考虑管道内水流混声、检测设备自身振动等多因素影响，基于现场声呐扫描采集的98万个点云坐标进行数据去噪和管道特征提取。在采用密度聚类优化算法进行点云数据初筛的基础上，提出圆外切线斜率拟合算法，相较于单一聚类算法能够更有效识别出排水管道内壁界限和淤积线，所得结论如下：

(1) 本文所提方法在保留管道原始特征的同时，去除了点云数据中所包含的大量噪声点，并得出最终的排水管道内壁界限和淤泥淤积拟合曲线。

(2) 通过分段圆外切线斜率拟合方式，可以有效识别出排水管道内壁特征，避免多元拟合所带来的管壁局部信息缺失问题。

(3) 试验结果表明，相比于用原始数据直接进行密度拟合，本文提出的方法有效提高了拟合的精度，拟合结果更加稳定。

由于声呐在扫描过程中不能保证呈直线运动，如何实现变化圆心点的管道内壁扫描截面拼接，从而得到整段排水管道的三维模型，将是下一步的研究重点。