电力市场背景下的近用户侧储能站容量优化配置研究

徐天韵，陈涛，高赐威

（东南大学 电气工程学院，南京 210096）

0 引言

如今，随着化石能源危机和环境保护问题日益突出，世界能源格局发生了重大变化，越来越多的可再生能源（如风能或太阳能）代替了化石能源被部署到输电和配电网中。这些清洁能源具有波动性和不可预测性，其频率波动、出力波动从数秒到数小时，电能质量相比传统能源差，增加了电网频率调控的需求，给电网的安全运行带来挑战［1］。因此，寻求新型调频手段提升电网调频能力成为目前的研究热点。电池储能系统具有响应快速、控制精度高、功率-频率特性优异等特点［2］，因此在参与电网调频这方面具有很大优势。在我国，大型储能电站正处于发展阶段。近年来江苏、河南、湖南、青海等省份百兆瓦级电池储能系统成功投运，验证了大规模储能电站快速响应、精准调频等作用［3］。

目前，国内外学者已针对储能系统参与电网频率调节开展了研究，大量的研究集中在电池储能系统的规划层面。文献［4］开发了一个随机模型——预测-控制框架来评估电池参与频率调节市场的效益，使用Ledoit-Wolf 协方差估计器，通过历史数据生产负载和价格来实现规划。文献［5］研究了以储能系统在辅助服务市场的收益最大化为目标，进行一次调频的优化和控制策略。文献［6］提出了基于机会约束规划的储能参与风电场一次调频的容量优化方法，建立以风储系统运行成本最小为目标，以满足一次调频需求为约束的优化模型。文献［7］基于全寿命周期理论，运用净现值法结合仿真模型构建储能电池参与一次调频的技术经济模型，以经济性最优和调频效果最优设计了储能电池参与一次调频的充放电策略。文献［8］对储能系统独立提供一次、二次调频情境下的日前市场申报策略优化方法进行研究，建立基于场景集的随机规划模型，并将其转化为混合整数线性规划问题进行优化。文献［9］考虑电池退化约束和频率调节性能评分，得出电池储能系统参与宾夕法尼亚州-新泽西州-马里兰州（PJM）频率调节市场的最优控制和提供算法。文献［10］提出一种考虑新能源出力和负荷不确定性的储能电站规划方法，构建了面向源-荷不确定性的储能电站双层规划模型。

另一方面，储能系统可以在正常运行状态下参与能源市场进行套利，从而获得收益。关于储能系统参与市场，文献［11］提出了一个在日前市场和实时市场中寻求利润最大化的电池储能系统的随机规划公式，对储能的经济可行性进行评估。文献［12］提出了一种动态规划方法来优化储能系统的实时运行决策，用于能源套利和频率调节，利用问题的嵌套结构，通过在不同的时间尺度上用简化的状态空间求解。文献［13］提出了一种储能参与现货市场联合竞价的双层Stackelberg 博弈模型，建立了以储能为竞价主体，兼顾收益与风险的现货市场联合竞价策略双层模型，利用对偶理论和KKT（Karush-Kuhn Tucker）最优性条件，将双层模型简化为一个均衡约束数学规划问题进行求解。

虽然已有大量国内外文献对于储能系统的频率调节和能源套利进行了研究，并且在储能系统电池的实时控制和运行方面取得了很大进展，但大多都预先假定了储能系统的大小［14-15］。对于储能系统的容量配置，并没有系统的经济模型为基础，文献［7］提出的储能电池参与一次调频的容量配置方法，虽然其全寿命周期的成本模型较为成熟，但并没有定量分析调频的效益。

基于现有研究的不足，本文主要针对电池储能系统参与电网频率调节和能源套利的容量配置进行研究。提出一种配电网中电池储能系统规模和运行的优化方法，构建了储能电池参与频率调节和能源套利的经济性模型，以储能系统成本最小化为目标，综合考虑电池寿命等因素，将其构建为一个非线性规划模型，并通过线性化的数学方法，将其转化为线性规划问题。最后，通过算例验证所提出优化方法的有效性并得出结论［16-17］。

1 储能系统模型构建

1.1 模型假设

本文重点研究了如何规划和评估电池储能系统项目，以主要参与频率调节市场。同时，该储能系统还可以参与能源套利，即在电价较低和较高时分别进行充电和放电，以获取利润。本文假设该电池储能系统每小时只能参与频率调节或者能源套利。如果储能系统只参与频率调节和能源套利，则该储能系统的选址无关紧要，在本文中并不讨论。同时，本文假设导体的载容量满足储能系统与电网之间的电力交换，在这种情况下，不需要对交流潮流进行约束。电池储能系统运行示意图如图1 所示。控制中心通过信号传输线与储能系统互联，发送实时的控制信号和电价。储能系统与电网通过变电站相联。储能系统通过与变电站交互功率以及本身调频或套利的充放电来满足负荷需求。

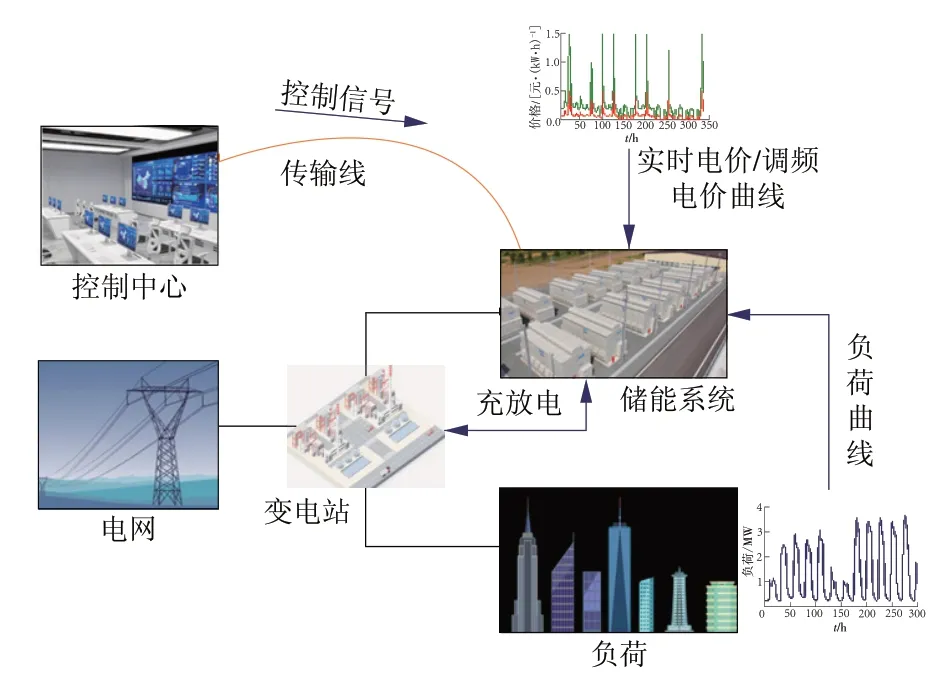
图1 储能系统运行示意Fig.1 Operation of an energy storage system

1.2 目标函数

储能系统参与频率调节和能源套利的目标函数如下［18］，该目标函数以成本最小化为目标。

式中：cInv为年化投资成本；cEne为年能源费用；cRev为年调频市场收益（由于目标函数的方向是成本最小化，因此从成本中减去收益）；cF，B为储能系统的固定投资成本，元；cE，B为储能系统每单位能量的投资成本，元/kW；cP，B为储能系统每单位功率的投资成本，元/kW；和分别为t时刻储能系统参与频率调节的放电和充电功率，kW；为t时刻储能系统的充放电功率（充电时为负，放电时为正），kW为电池储能系统在t时刻与变电站的交互功率（变电站输出能量时为正，否则为负），kW·h为储能系统的功率容量，kW；xB为二进制变量，建设储能系统时为1，否则为0；r为年利率，%；N为储能系统寿命，年；B为充放电1 kW·h 电池老化成本，元；PSt为电池储能系统在t时刻与变电站的交互功率（变电站输出能量时为正，否则为负），kW；cSt为t时刻的电价，元/（kW·h）；S为储能系统参与调频的性能评估系数为t时刻频率调节出清价格，元/（kW·h）；βreg为里程比。式（2）从净现值的角度考虑了在一个投资周期中建设一个电池储能系统的年化投资成本，具体为储能系统的固定投资成本、考虑能源容量的成本、考虑功率容量的成本和储能电池退化的成本之和。同时，考虑电池寿命的折损成本。对于储能电池退化过程的成本折算比较复杂，受到电池种类、规模、运行方式等因素的影响［14］。式（3）考虑了在一个时间段内，能源市场的清算价格与储能系统同变电站的交互功率，即为系统参与能源套利的成本。

本文中对电池的退化模型作简化处理，把电池寿命的折损成本定义为电池组的能量成本，即式（2）中的B，该折损成本的计算如下

式中：K为电池更换成本；L为电池寿命吞吐量，kW·h；E为电池往返效率的平方根，%。该模型将电池寿命的折损成本折算为电池充放电1 kW·h 的成本［14］。

公式（4）考虑了储能系统参与调频时的预留功率和实际充放电功率对收益的影响。PJM 承诺对提供频率管理的资源采用两部分的支付模式，分别是调频市场容量清算价格（RMCCP）和调频市场表现清算价格（RMPCP）。PJM 提供了2 种调节信号，一种是调节信号A（Reg A），针对传统的发电机资源，另一种是低通滤波区域控制误差信号；调节信号D（Reg D）是专门为电池储能系统等可以几乎瞬时跟随信号而响应的系统设计的，是一种高通滤波的控制误差信号［15］，里程比的计算方法为调节信号D 与调节信号A的里程之比，如下

1.3 约束条件

对于电池储能系统的成本，除了与上述提及的一系列投资成本有关，还与系统与变电站交互功率、功率和能量最大容量、电池组荷电状态（State of Charge，SOC）、系统参与调频充放电功率等因素有关，需要满足下述约束条件

式（7），（8），（9）为系统规划阶段的约束条件。约束（7）和（8）分别限制了电池储能系统的功率和能源的容量。约束（9）对于规划储能系统的投资预算进行了限制。

式（10）—（18）为储能系统运行时的约束条件。

约束（10）是变电站节点功率平衡方程。在一个时间段内，储能系统与变电站交互的功率以及参与调频和套利的电池充放电功率需要满足当前时刻负荷的需求。

约束（11）限制了储能系统和变电站的功率交换。

约束（12）和（14）表示储能系统参与能源套利和频率调节的充放电功率收到其功率容量的限制。

约束（13）表示储能系统参与频率调节时的充放电功率为频率调节信号与系统参与调频预留功率之积。其中和分别是储能系统参与调频时电池充放电功率，两者均为正值。在模型的构建中，本文将调频时的充放电功率分开成2个变量，原因在于储能系统参与调频市场时，收益无关于电池组充电或放电。若将其定义为一个统一的变量，则需要通过正负号来区分放电和充电，如此构建出的收益模型是非线性的。本文将其分开为2 个变量，在一定程度上将模型复杂化，但是避免了此处造成的模型非线性问题，也简化了后文将模型线性化的过程。

约束（15）根据电池SOC 的范围约束了储能系统的能量等级。

约束（16）表示储能系统中由于能源套利和频率调节的功率充放电而产生的能量平衡。

约束（17）和（18）说明了储能系统的能量、功率等变量的范围和类型。

需要注意的是，上述的约束条件须在任意时间段内都满足。

1.4 线性化

在上述约束（12），（13），（14）中，由于通过二进制变量来确定储能系统是参与调频还是套利，以及确定储能系统参与频率调节时的充放电，造成了二进制变量与连续变量相乘导致的非线性。为了简化模型在求解时的计算量，本文对上述非线性模型进行了线性化，具体线性化后的约束条件如下

需要注意的是，所提出的算法从经济的角度来确定是否安装电池储能系统。在此问题中，储能系统通过能源价格和调频价格在一个时间段内进行充放电来进行能源套利或者频率调节。这是一个长期的规划问题，不涉及实时的操控。上述提及的储能系统投资成本的经济模型经过线性化后转换为一个线性规划问题，可以通过成熟的规划求解器来进行求解。

2 案例分析

2.1 案例选择

在第1 部分中，本文提出了一个电池储能系统参与能源套利和频率调节的线性化经济性模型。本节所提出的优化模型用于一个真实的案例，该案例提供了历史数据包括负荷数据和实时电价等。

本文的案例研究所在地是山西省。根据国家发改委2019年印发的《关于全面放开经营性电力用户发用电计划的通知》明确推进经营性用户全部进入市场。2020 年国家发改委再次重审逐步取消工商业目录电价。2021年10月，国家发改委发布关于进一步深化燃煤发电上网电价市场化改革的通知，要求取消工商业目录销售电价。目录电价的逐步取消，意味着市场化用户的电价界限被取消，随之电价会随着市场的供需关系而波动。作为电力现货市场的试点省份，山西省电价波动幅度会更大，其峰谷价差达到 1.5 元/（kW·h）左右。

本文将电池储能系统建立在山西省一座商业综合楼宇，该楼宇为国际甲级写字楼。建筑于2007年建成并正式投入运行，目前出租率为95%。建筑地上35 层，地下5 层。建筑总高度为161.5 m，总建筑面积约64 648 m2。建筑B1～B5 为车库和设备用房，5F，6F，21F，22F，37F，38F 为设备层，3F～4F 为餐饮，其他区域为办公楼。需注意的是，储能系统的选址并不是本文的分析内容，选择该案例仅用于研究所提出优化模型的准确性。在时间的选择上，本文选择了2020 年12 月1 日—31 日这31 天。每一天中选择24 个数据点，即以 h 为单位进行数据选择。需要注意的是，本文并没有采取选择典型日的方式来选取数据，而是选择了12 月这一连续的时间段。原因在于：对于典型日的选取，在数据量不大的情况下，由于工作日与周末，月初、月中与月末的电价和负荷会存在不同程度的差异，难以比较准确地替代整体数据。

用于该案例中的优化模型具体参数取值见表1，该案例的负荷特性曲线和实时电价以及调频电价曲线如图2—3所示。需要注意的是，由于我国目前缺乏调频市场数据，案例中用到的频率调节的出清价格来自于假设。根据实际案例的数据，实时电价与调频出清价格显著相关，本文将真实的实时电价数据进行等比例缩放并加之随机扰动得到图中的调频出清价格。

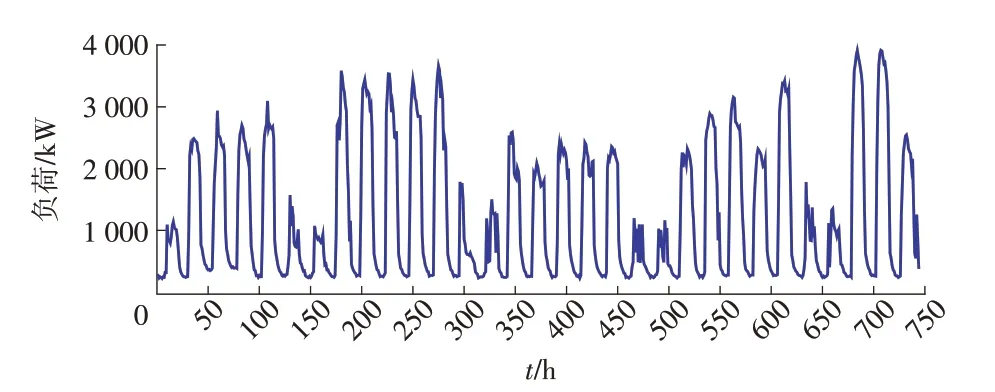
图2 负荷特性曲线Fig.2 Load characteristic curve

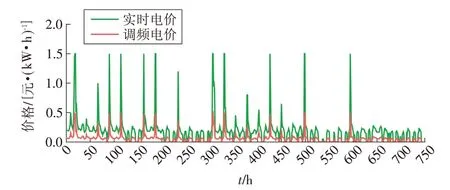
图3 实时电价和调频电价曲线Fig.3 Real-time and frequency regulation prices

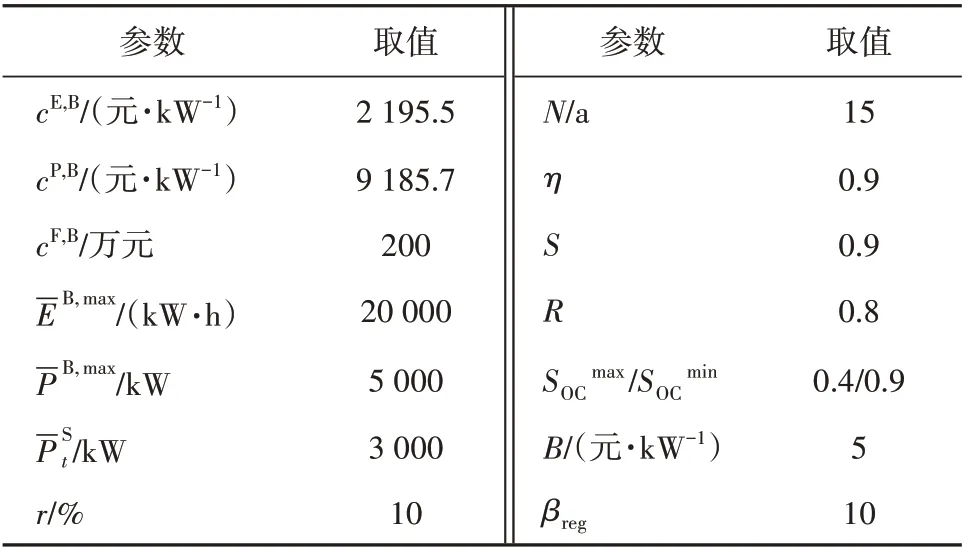
表1 模型参数取值Table 1 Parameters of the model

2.2 结果分析

本案例中，设置储能系统的功率（-PB，max）和能量上限（-EB，max）分别为5 MW 和20 MW·h。固定的成本系数（cF，B）为200 万元，能源成本系数（cE，B，cP，B）分别为2 195.5 元/（kW·h）和9 185.7 元/kW。此外，电池储能系统的寿命（L）和年利润（r）分别设置为15 a和10%。对于储能系统电池组的SOC 范围以及充放电效率，本案例中设置为0.4～0.9和0.9。需要注意的是，其中部分参数不来源于真实的案例数据，而是本文作出的假设，设置可以根据具体情况作出调整。在本文之后的敏感性分析中，会做具体分析。

根据本文提出的基于能源套利和频率调节的优化算法，通过基于Python 语言的Pyomo 开源软件包，利用Gurobi 求解器进行模型求解。经过规划求解，可以确定储能系统的功率容量（-PB）和能量容量（-EB）分别是4.227 MW 和12.175 MW·h，该储能系统的总投资成本为6 755 万元，月利润为314 443元。规划求解得到的每时刻储能系统参与调频或套利的充放电数据如图4 所示，储能系统的储能变化如图5所示。

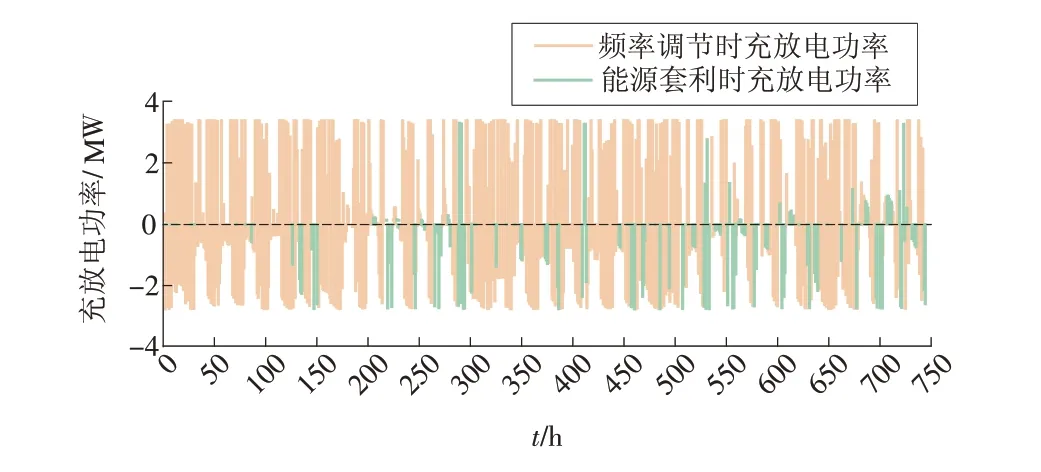
图4 储能系统参与调频或套利的充放电功率Fig.4 Charge and discharge power of the energy storage system participating in frequency regulation or energy arbitrage

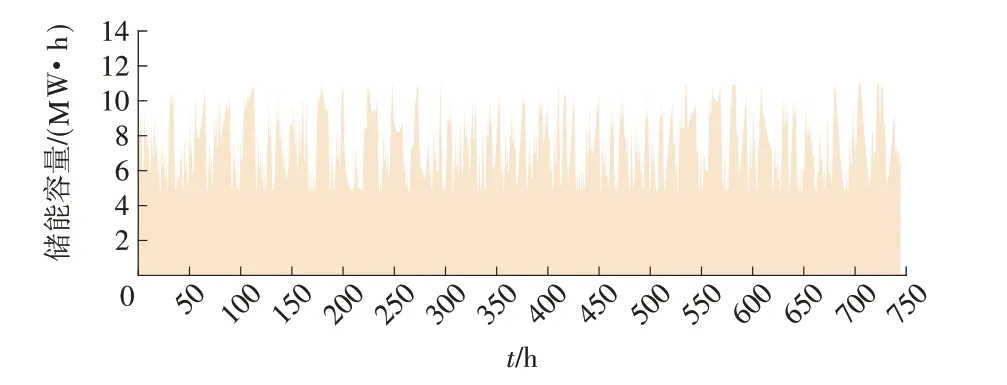
图5 储能系统容量变化Fig.5 Variation of the energy stored in the system

根据对求解数据的分析，在31 d 的 744 h 内，有132 h 储能系统在参与能源套利，另外的612 h 储能系统在参与频率调节。由此可见，大多数时候储能系统运行在调频的状态下，储能系统的能量含量也会发生相应变化。从所获得的收益也可以看出，储能系统的利润主要来源于频率调节。对比图3和图4 可以发现，储能系统能源套利实际上并不一定在电价低时充电或者电价高时放电。系统在电价较高时也出现充电现象，这是为了保证系统的储能和下一步进行的频率调节。这也说明，储能系统能够从参与频率调节相比于能源套利获得更大的利润。

2.3 敏感性分析

2.3.1 参数变化的敏感性分析

下文就本文所提优化算法用于具体算例进行敏感性分析，以分析优化算法中参数对计算结果的影响。在上文提出的目标函数中，将收益作为负成本处理，而在下文的敏感性分析中，采用储能系统的收益来评估，可以更加直观地体现出该储能系统优化模型的可行性。

如图6 所示，通过改变建设储能系统设置的最大功率（-PB，max）的大小，分别将其设置为1，2，3，5，10 MW，其他参数按上述具体案例中的取值不变，来分析储能系统的利润、功率（-PB）及能源容量（-EB）的变化。由图6可知，在其他条件不变的情况下，储能系统通过能源套利和频率调节获得的利润与最大功率（-PB，max）并非正相关，当最大功率（-PB，max）增长时，利润会随之先增长后减少，而能源容量（-EB）变化不大。实际上确定的功率（-PB）会随着最大功率的扩大而固定在某一个值。

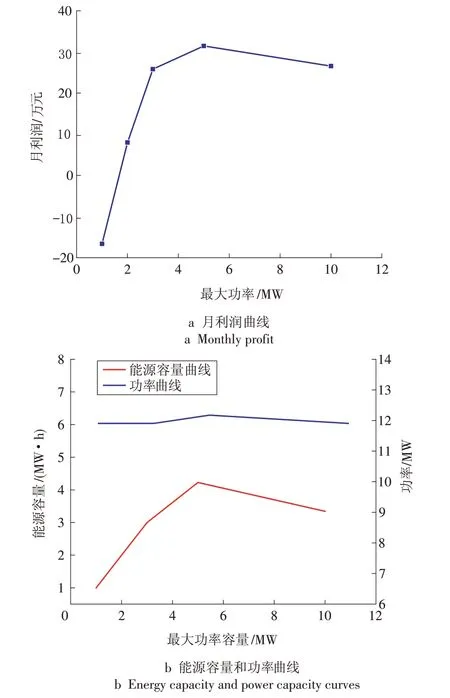
图6 储能系统最大功率的敏感性分析Fig.6 Sensitivity analysis on the maximum power capacity of the system

表2通过改变性能评分（SFR）这个参数来分析该参数对于储能系统利润的影响。该参数是对资源遵循调节信号程度的一种评估，可以包含3个部分，分别是延迟评分、相关性评分和精度评分。现有研究证明，电池储能系统的性能评价是很好的，在0.90～0.98［16］。在本文之前的案例研究中将该参数取为0.90，现通过改变该参数的取值分析计算结果的变化。分析可知，性能评估的取值越高，储能系统的能源容量（-EB）越小，储能系统的利润随之变大。

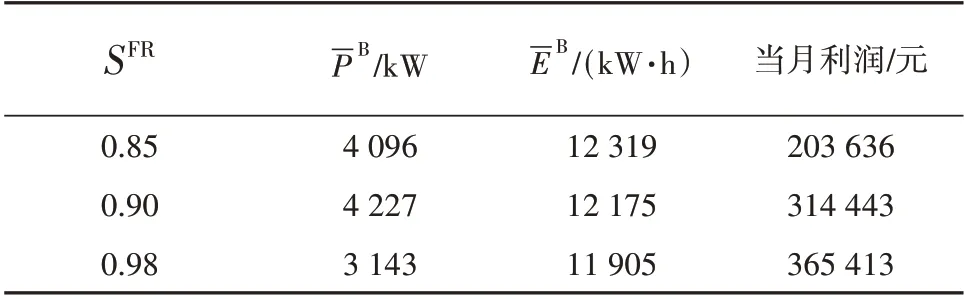
表2 性能评分的敏感性分析Table 2 Sensitivity analysis on the performance indexes

2.3.2 电价波动幅度变化的敏感性分析

上文提到，国家正在逐步出台政策取消工商业的目录电价，这可能导致电价的波动变化更大，在此处的敏感性分析中，将就电价波动变化对于电池储能系统的影响进行分析。

案例中采用山西省的真实电价数据，本文通过数据处理改变其波动幅度。山西省采用的是分时电价，本文将通过在08：00—20：00 以及20：00—次日08：00的数据中分别加以一定范围内不同方向随机扰动的方式（见表3），来调整电价的波动幅度。

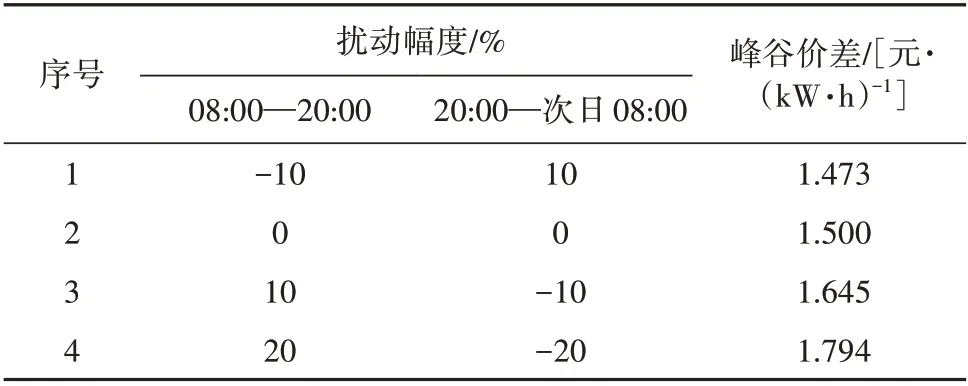
表3 分时扰动幅度参数Table 3 Perturbation amplitudes in different time intervals

模拟得到峰谷电价差最大1.794元/（kW·h），最小1.473 元/（kW·h）（真实数据为1.5 元/（kW·h））。经过本文所提出的优化算法求解得出对应4种电价波形曲线结果（见表4），从结果可以看出，尽管电价的波动程度发生了改变，但对于电池储能系统来说，其利润变化不大。

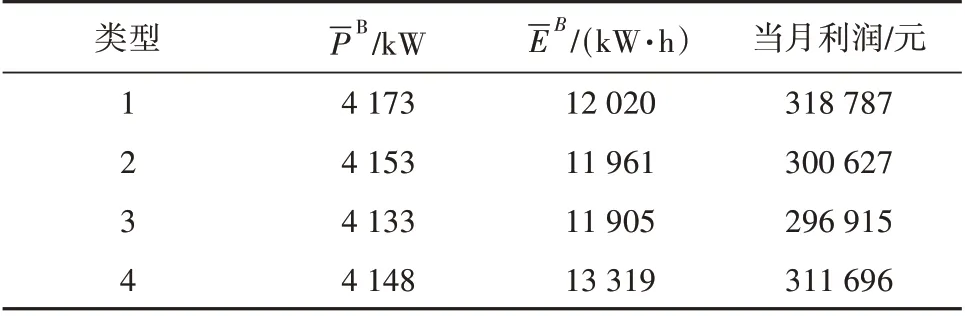
表4 对应4种电价波形的求解结果Table 4 Solutions for the waveforms of four electricity prices

3 结论

为了实现近用户侧储能电池参与电网调频辅助服务及能源套利，本文提出了电池储能系统的容量优化配置方法。本文以储能系统总和成本最小化为目标，建立了储能系统参与调频和套利的经济模型，通过线性化方式构建出一个线性规划问题并进行求解。基于真实案例和历史数据分析，证明了本文所提出的优化算法可以准确、有效配置储能系统的功率和能源容量，并合理参与电力市场交易。从而得出的结论如下。

（1）储能系统参与频率调节市场获得的收益通常高于其参与能源套利获得的收益。

（2）对于储能系统的定容问题，其功率主要取决于设定的最大功率限制，其能源容量主要取决于参与调频市场的相关参数，如调频价格和性能评估。

（3）电力市场未来政策进一步放开定价体系，可能导致电价波动性增强、峰谷价差增大，电池储能系统投资规划将受到一定程度影响。