在创设“问题情境”中发现数学
——以“初识圆锥曲线”一课为例
2023-03-20王文杰
王文杰
(江苏省苏州工业园区星海实验中学 215021)
《普通高中数学课程标准(2017年版)》(下称《标准》)在教学建议中提出:基于数学学科核心素养的教学活动应该把握数学的本质,创设合适的教学情境、提出合适的数学问题,引发学生思考与交流,形成和发展数学学科核心素养[1].那么教师如何在问题情境中引导学生发现数学,培养学生发现问题和提出问题、分析问题和解决问题的能力?笔者在一次省外教学交流活动中开设研讨课“初识圆锥曲线”,对数学课堂教学中实践“问题情境中发现数学”进行了尝试与探索,现将教学过程及思考总结整理如下,与同行分享.
1 教学分析
关于本课教学内容,在高中数学人教A版选择性必修第一册第三章“圆锥曲线的方程”的前言里,只简单叙述了用平面截圆锥面得到圆锥曲线.而本节课研究的主要目的是要让学生感受到“数学知识”与“现实生活”的紧密联系,学会看到生活中的数学问题,即“学生会用数学眼光观察世界”.另外,本课从“感知静态的圆锥曲线”到“探索动态的圆锥曲线”,既符合圆锥曲线发现和研究的历史,渗透数学文化,又遵循学生认知的规律,知识研究循序渐进.
教学目标 (1)通过平面截圆锥面,感知静态的圆锥曲线;(2)通过创设情境,探索动态的圆锥曲线,发现圆锥曲线的特征,掌握圆锥曲线的定义;(3)会用数学眼光观察世界,感悟数学文化,提高发现和提出问题、分析和解决问题的能力.
2 教学过程
2.1 设置情境,引出问题
情境1 生活中你见过这些图形吗(图1)?

图1
师:同学们,我们生活中见过这些图形吗?我们看到过哪些特别的曲线?
生(合):见过……
设计意图借助学生身边常见的图形,激发研究兴趣,逐步引出研究的问题.
情境2 观察圆锥形酒杯的液面,发现水平放置时与微倾时液面图形有何变化(图2)?

图2
师:请观察老师手中酒杯的液面,有什么变化?
生:圆锥形酒杯中液面从一个圆面变成了一个“扁圆”面.
师:轮廓曲线呢?
生:从圆变成了“扁圆”.
师:那什么是“扁圆”?“扁圆”又具有怎样的特征呢?
设计意图用生活实例现场演示,让学生“真”观察,进一步激发探究热情,并引导学生要善于观察生活,善于发现问题.
情境3 公元前3~4世纪,不少古希腊学者在圆锥面中用截面截得不同的曲线.请4~5位同学合作:观察课桌上的几何模型(图3),若用一个平面截该模型,可以得到几种曲线?
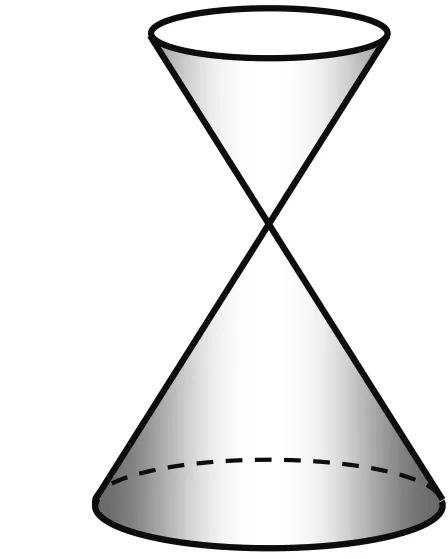
图3
学生观察讨论后,教师动态演示结果(图4).

图4
生:……
师:我们分别称其为椭圆、双曲线、抛物线.又因为这三种曲线最早都是由截圆锥面得到的,所以又将其统称为圆锥曲线.
师:今天我们重点研究圆锥曲线中的椭圆.
设计意图历史文化与现代科技结合,让学生“知其然”又“知其所以然”.
情境4 模拟点光源投影实验.
师:如果点光源位于球心的正上方,平面上的投影是个圆面,轮廓曲线就是个圆(图5);如果点光源稍微偏离正上方一点,平面上的投影是个椭圆面,轮廓曲线就是个椭圆(图6),其实就相当于情景3中的平面截圆锥面得到的曲线椭圆.
师:类比圆的特征,你能发现椭圆的特征吗?
生:圆上的点到切点(圆心)的距离等于定值.椭圆上的点到切点的距离不等于定值.
师:为什么不是定值?
生:因为切点有点偏在右侧.
师:提醒一下,椭圆图形好像也有对称性的,如果考虑对称性,左侧是不是也应该有个切点比较合理?这个切点怎么得到呢?我们可以在投影的下方放一个球,这个球与上方的球一样,满足:与投影面相切,与圆锥面相切(图7).当有两个切点后,你的想法是什么?
生:曲线上的点到两切点的距离之和是否是定值?
师:好.下面我们一起来证明它.如图7,过点M作圆锥面的一条母线分别交圆O1,圆O2于P,Q两点,因为过球外一点作球的切线长相等,所以MF1=MP,MF2=MQ,所以MF1+MF2=MP+MQ=PQ,即MF1+MF2=定值.
师:上面的证明,最早是在1822年由比利时数学家丹德林(1794—1847)发明的,我们将其称为丹德林双球实验.
设计意图考虑数学课堂上实现点光源投影实验有一定难度,且为避免教学重点“本末倒置”,所以简化为模拟点光源投影实验,既让学生体会到生活实例的熟悉感,又快速引出对椭圆定义的研究.
2.2 数学建构,探究问题
问题:类比“圆”的定义,你能给出“椭圆”的定义吗?
师:平面内到一定点O的距离等于定值(定值大于零)的点的轨迹叫作圆,这个定点叫作圆的圆心,定值叫作圆的半径.那么椭圆的定义呢?
生(讨论后,合作补充完成):平面内到两定点F1,F2的距离的和等于常数(大于F1F2)的点的轨迹叫作椭圆,两个定点F1,F2叫椭圆的焦点,两焦点间的距离叫作椭圆的焦距.
设计意图通过生活中实例、问题情境的引导,学生发现数学问题,并将发现的“数学”抽象概括,培养数学的核心素养能力.当然抽象概括数学的概念、性质、定理等都是数学教学的难点,学生的数学抽象能力不是一蹴而就的,但是也不能因“数学抽象”是难点就避而远之,读教材、抄板书是培养不出学生的数学抽象能力的.本节课在数学知识建构时,引导学生思考“圆的定义”,教会学生用“类比”开放式的思维方式去抽象概括,并以师生合作、生生合作的方式慢慢“打磨”椭圆概念,以此培养能力,提升素养.
2.3 数学运用,解决问题
例由2~3位同学合作,试用所给的棉线画出一个椭圆.
师:你确定你画的曲线是“椭圆”吗?若是,请说明理由;若不是,也请找出问题.
设计意图学会运用数学的眼光观察世界,生活中处处都是数学,学生拿着一条棉线画出一个个“圆扁不一”的图形时,心中已经感受到数学无限的魅力.当然教师会充分挖掘“圆扁不一”的图形的价值,追问学生:所画图形是不是椭圆?如果是,理由呢?如果不是,为什么?进而让学生看着自己画的“圆扁不一”的图形,进一步认识椭圆的定义,内化数学知识,升华教学重点.
3 教学反思
3.1 “问题情境”是学生发现数学的窗口
本节课的四个问题情境,从静态初识“圆锥曲线”到动态初识“圆锥曲线”,从生活中的“圆锥曲线”到数学图形中的“圆锥曲线”,从感性地发现“圆锥曲线”到理性地证明“圆锥曲线”,既符合数学历史上发现与发展的客观实际,又遵循学生发现数学的认知规律.《标准》中指出:“教学情境和数学问题是多样的、多层次的.教学情境包括:现实情境、数学情境、科学情境,每种情境可以分为熟悉的、关联的、综合的”[1].所以教师设计的问题情境不仅要很好地引出新知,更要在潜移默化间让学生感受数学知识与现实世界之间的密切联系,要简洁高效、精彩有效、科学正确,不能“哗众取宠”“喧宾夺主”,也不能“简单堆砌”“不知所云”,更不能“歪曲历史”“违背科学”;教师设计的问题情境要结合现实生活、研究数学文化、综合其他学科的知识,要洞悉学生的学习“兴趣点”、了解学生知识的“最近发展区”,要把握课堂教学的方向和目标,要让学生感到既“远”又“近”、既“陌生”又“熟悉”、既“精彩”又“科学”.只有这样设计的问题情境才是学生喜爱数学、发现数学的窗口.
3.2 “问题情境”是学生思考数学的引擎
高中数学课程学习要提高学生从数学角度发现和提出问题的能力、分析和解决问题的能力,这就要求教师设计的问题情境是多样的、多层次的、变化的、灵动的.例如:本课师生探究情境2时,学生课堂意外生成“扁圆”,教师借力追问:“什么是‘扁圆’?‘扁圆’又具有怎样的特征呢?”;当学生用棉线画出“圆扁不一”的图形时,教师适时提问:“你确定你画的曲线是‘椭圆’吗?若是,请说明理由;若不是,也请找出问题.”教师要做好学情分析,了解学生的兴趣点、挖掘学生身边的数学素材、把握知识之间的相互联系,善用“追问”提好问题,让学生在“问”与“答”之间、“思考”与“再思考”之间,学会用数学眼光观察世界、用数学思维思考世界、用数学语言表达世界,让学生在思考和解决问题的过程中,理解数学内容的本质,只有这样设计的问题情境才是学生思考数学的引擎、学生核心素养培育的点火器.
