基于PSO-PID 的拖拉机线控液压转向控制研究*

周达辉 ，赵山虎 ，王涤成 ，魏国俊 ，周俊博 ，肖茂华

（1.江苏省农业机械试验鉴定站，江苏 南京 210017；2.江苏悦达智能农业装备有限公司，江苏 盐城 224100；3.南京农业大学工学院，江苏 南京 210031）

0 引言

拖拉机转向控制系统是保证拖拉机行驶安全性和作业效率的重要系统。作为我国农业生产所不能缺少的动力机械，拖拉机是我国农业机械化、现代化水平的重要保障。拖拉机工作质量直接影响着农业生产质量，所以设计一台适应于拖拉机运行特性的转向控制系统，提升拖拉机行驶安全性和作业效率，已经成为一项关乎国计民生的重要问题[1]。

线控式液压操纵装置的控制系统是闭环控制，实质上是一个非线性、时变系统。另外，由于拖拉机实际驾驶工作条件恶劣，车轮和地面之间产生的摩擦力也非常复杂[2]。传统PID 闭环控制计算通常是针对线性化控制系统模型，以简单的PID 控制算法来实现非线性、时变控制系统的位置闭环控制时，工况出现变化将会导致系统其他参数发生变化。而且PID 控制算法需要准确整定PID 参数，若参数整定经常不理想，闭环控制系统的性能将会下降，甚至达不到控制目标的要求，结果会使系统性能大大降低[3]。因此，针对拖拉机转向系统等运行环境恶劣的非线性、时变系统需要采用正确的闭环控制方法。

近年来，人工智能控制算法飞速发展，粒子群算法因具有人类抽象思维的功能，在工业生产控制系统中得到了广泛应用。课题组通过PSO 算法对线控液压转向控制系统的PID 控制器三个参数进行动态调整，以使整个控制系统达到最高性能指标，主要使用Simulink 模块仿真，探究粒子群算法优化的PID 算法。

1 线控液压转向系统的基本结构

线控液压转向装置的基本结构如图1 所示，整个转向装置由方向盘子系统、电气控制单元、液压和机械控制单元构成[4]。方向盘子系统主要包含路感电机和方向盘转角传感器，通过方向盘转角传感器可以测得驾驶者的转向意图信息，通过路感电机可以供给方向盘阻力矩使驾驶员感知到道路行驶状态。电气控制单元对所收集到的方向盘旋转信息、油压数据等加以处理，并传递目标转角信息至执行元件中，它还能够对驾驶员的操纵信息加以鉴别，从而判断在当前情况下驾驶员的方向盘动作是否正确。当车辆处在非平衡状况下或判断驾驶员产生了错误信息后，前轮线控转向装置就会主动调整纠正驾驶员的错误转向动作，从而使拖拉机尽快恢复至平衡状态。液压执行部分采用电液伺服阀控制进入转向油缸的流量推动活塞杆运动，进而带动机械执行部件转向梯形运动，最终使得前轮实现转向运动。

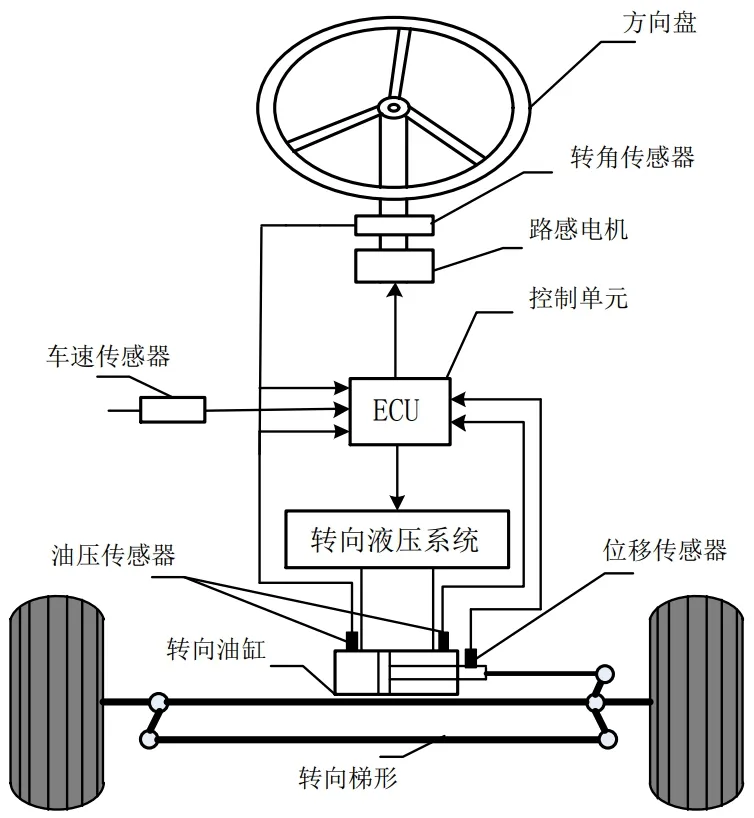
图1 线控液压转向系统基本结构图

2 线控液压系统的控制策略

2.1 PID控制

PID 控制是一种基于反馈控制的控制方法[5]。PID 控制系统结构图[6]，如图2所示。

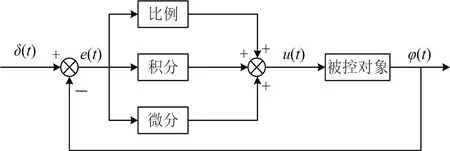
图2 PID控制系统结构图

PID 控制器是把前轮转角信号δ(t)与通过传感器反馈回路的转向缸实际位移输出信号φ(t)作差，获得移动差分e(t)，接着对差分e(t)经过比例、积分、微分计算并求和，获得调节量u(t)并调节被控对象。PID控制过程的数学表示如下：

式中，u0为PID 控制器初始量。

由式（1）知，PID 控制器的核心是对误差实行比例、积分、微分的三个计算过程[7]，由于三者计算相互独立，因此控制器效果的好坏完全依赖三者综合计算的结果，所以通过对比例系数、积分系数、微分系数三种参数的合理选用，可以使控制器达到目标效果。

2.2 粒子群算法（PSO）

粒子群算法，亦称为粒子群优化方法或鸟群觅食方法（Particle Swarm Optimization, PSO）[8]。粒子群算法是一种种群算法，种群中所有个体为粒子，所有粒子均被视为潜在的可行解，种群中食物的位置为全局最优解。粒子在解空间中，通过跟踪个体和群体极值确定最优解方向即各粒子位置和速度，每更新一次位置则计算一次适应度，再通过比较粒子个体和群体极值的适应度更新个体和群体极值[9]。

粒子群算法的数学表述如下：假定种群规模为N，迭代的时间为t，则每个微粒群在D维空间中的位置坐标都可描述为；粒子的速度表达式为。坐标位移xi(t)和速率vi(t)在t+1时刻可以根据以下方法加以调整：

式中，c1、c2表示学习要素；r1、r2表示(0,1)期间的随机数；pi(t)为个体最优解；pg(t)为全局最优解。

公式（2）中惯性权重ω描述了微粒的运动惯性对此粒子速度的直接影响，取值程度可调控PSO 的全域与局部寻优功能。ω比较大时，粒子的全局搜索能力较强，此时收敛速度虽然很快，却不容易得到精确解；ω比较小时，粒子的局部搜索能力强，但是容易陷入局部收敛[10]。因此，本文通过线性权值降低的方法对ω实现动态调整：当算法开始时，可给ω赋予较大的正值，随着算法的执行，可使ω线性地减小，由此使得粒子在算法初期能够以较快的速度探索最优值区域，而在算法后期能够在最优值区域进行精细搜索，从而使算法有较大的概率向全局最优解位置收敛，其表达式如式（4）所示：

式中，Tmax代表最高进化代数；ωmin为最低惯性权重；ωmax为最高惯性权重；m表示当前迭代次数。

3 基于粒子群算法（PSO）的PID 控制器参数寻优

使用MATLAB 实现PID 参数设计优化模拟，建立相等随机因子计算过程如下：

1）首先初步化粒子群的各参量，并判断颗粒速度情况。

2）比较粒子适应度值。

3）将所有粒子适应值和粒子所经过的最优预测位置与粒子群所经过的最优预测位置适应值进行对比更新。

4）进行速度和位置更新。

5）判断是否满足终止条件，若不满足则回到步骤2。

前轮目标转角5°阶跃输入下、连续两次阶跃输入下、正弦输入下的两种不同调参方式下的PID 输出响应曲线分别如图3、4、5所示。

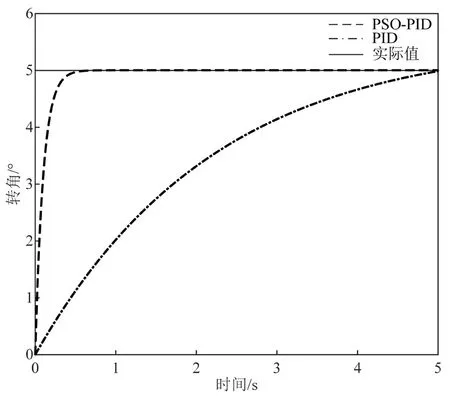
图3 前轮目标转角5°阶跃输入下两种不同调参方式下的PID 参数控制曲线

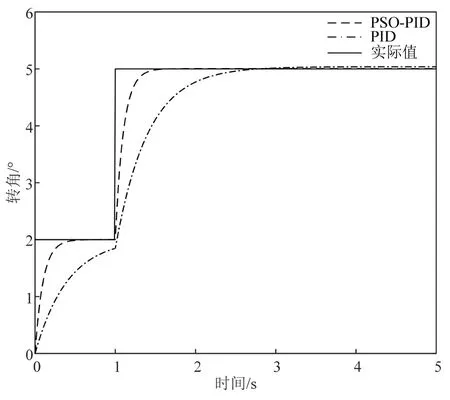
图4 连续两次阶跃输入下两种不同调参方式下的PID 参数控制曲线

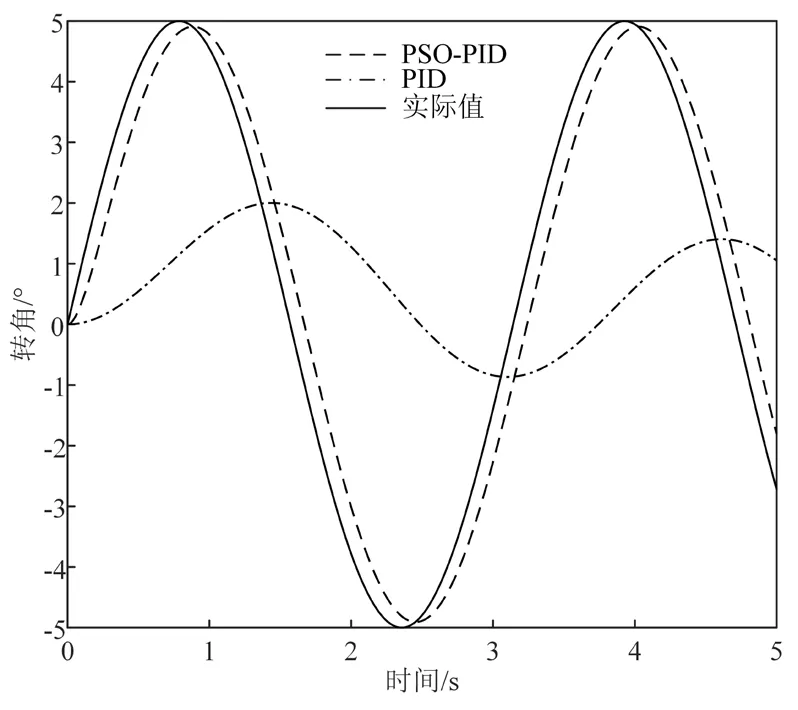
图5 正弦输入下两种不同调参方式下的PID 参数控制曲线

PSO 优化PID 参数后的PID 控制系统有着无超调量及响应时间快等优点。

4 总结

本研究采用了理论分析法及仿真实验法，对线控液压转向系统的模型进行了仿真分析，基于PSO 算法优化了PID 的3 个参数，并且得出了使整个PID 系统性能优异的优化结果，再对结果进行分析总结。

1）此次实验的结果比较准确，实验的仿真设计过程是完整的。

2）本仿真实验是在理想条件下进行的，例如拖拉机的负载是不变的，需对复杂工况下的线控液压转向系统进行进一步研究。

3）本仿真实验采用的PSO 算法本身具有局限性：易陷入局部寻优及随机性较大等问题，在Simulink 仿真过程存在几次误差较大的仿真结果。所以希望在以后的学习中加强对算法的理解，针对PSO 算法的局限性进行相应的优化，不断去学习研究以达到更好的实验效果。