基于优化多尺度排列熵和卷积神经网络的滚动轴承故障诊断方法

伍济钢，文 港

（湖南科技大学 机械设备健康维护湖南省重点实验室，湘潭 411201）

0 引言

滚动轴承作为燃气轮机、航空发动机等重要机械中关键的支承零件，经常工作在高载、高频以及高温的恶劣环境下，容易发生磨损、点蚀等诸多故障。为避免因滚动轴承故障而导致巨大经济损失甚至人员伤亡，对滚动轴承进行精确故障诊断是十分必要的[1]。

故障特征的提取是故障诊断的前提，而滚动轴承振动信号的传递路径复杂，并且滚动轴承与其他零部件的耦合运动会导致故障特征信号的多模态混淆，因此在进行故障特征提取时会面临故障特征信号微弱、信号非线性和多尺度特征难提取的问题[2-3]。针对这些问题，Huang 等[4]提出用经验模态分解（EMD）的方法将复杂信号分解为多个内禀模态函数（IMF），但该方法的模态混叠十分严重。胡茑庆等[5]针对行星齿轮箱振动信号的非平稳特性，通过EMD 分解后根据峭度值选择最优IMF，解决了信号非线性问题，但模态混叠仍严重。集合经验模态分解（EEMD）[6]能够改善EMD 带来的模态混叠问题：朱渔等[7]通过EEMD 和双向长短期记忆（BLSTM）对齿轮行星轮进行故障诊断，田晶等[8]通过EEMD 对滚动轴承故障信号进行分解以及IMF 重构，虽然改善了模态混叠问题，但是会给原信号带来残留的白噪声信号。自适应噪声完备集合经验模式分解（complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN）[9]能够极大降低EEMD 引入高斯白噪声而导致噪声残余的问题：肖俊青等[10]结合CEEMDAN 和深度学习的方法对滚动轴承进行故障诊断，刘起超等[11]通过CEEMDAN 对振动管道的压差信号进行分解，但是CEEMDAN 分解结果仍然存在一定程度的模态混叠问题。综上，虽然EMD、EEMD、CEEMDAN均能针对故障信号的非线性和特征信号微弱的问题予以一定程度的解决，但是模态混叠问题始终未得到很好的解决。Colominas 等[12]在CEEMDAN 基础上针对模态混叠问题进行改进，形成ICEEMDAN方法；但管一臣等[13]利用ICEEMDAN 方法对行星齿轮箱故障电流信号进行分解发现，该方法缺乏多尺度特征提取能力，不便进行精确的故障分类。可见，ICEEMDAN 虽能解决故障信号提取中的模态混叠和低效率问题，但是信号特征提取能力欠缺。

近些年，变分模态分解（VMD）和卷积神经网络（CNN）在故障诊断领域的应用较为广泛，以滚动轴承故障为对象，为了从噪声干扰下的复合故障信号中提取出有效的单一故障信息，张伟等[14]提出蝙蝠算法优化VMD 的分离方法，但是没有进行进一步的特征提取。为了提高旋转机械滚动轴承故障诊断的准确率，曹洁等[15]提出VMD 和反向传播神经网络（back propagation neural network, BPNN）的滚动轴承故障诊断方法，但是该方法将特征提取过程完全依靠BPNN，存在局限性。为了检测强噪声和变工况下的滚动轴承故障类型，赵小强等[16]提出了改进Lenet5 神经网络的轴承故障诊断方法，但将信号的特征提取过程完全交给Lenet5 这样一个黑匣子网络模型，难以保证关键特征的提取。为解决上述方法中在关键特征提取方面存在的问题，本文提出基于优化多尺度排列熵（multi-scale permutation entropy, MPE）[17]和CNN 的滚动轴承故障诊断方法，通过ICEEMDAN 进行信号的分解降噪以及关键特征的显化，再通过优化的MPE 进行关键特征提取，最后通过CNN 实现信号特征的非线性分类。

1 方法原理

1.1 ICEEMDAN 信号分解方法

本文通过ICEEMDAN 信号分解方法来解决滚动轴承故障信号特征微弱和非线性的问题。ICEEMDAN 在对信号进行多次分解和重构后可把信号区分为包含不同模态的IMF 分量，从而实现信号特征加强以及对非线性信号中各模态的区分。ICEEMDAN 和CEEMDAN 都是在每次分解后的残差中添加高斯白噪声后再进行EMD，均可极大程度消减模态混叠现象；但和CEEMDAN 把含噪声的IMF 平均后作为最终IMF 不同，ICEEMDAN把上次迭代的残差和本次含噪声的残差平均值之差作为本次迭代的IMF，可进一步减少无用IMF分量和模态混叠现象。ICEEMDAN 方法的具体运行流程如图1 所示，图中：x为输入的原始振动信号；β1、βk分别为第1 次和第k次分解信号时的期望信噪比；X1n、Xkn分别为构造的第1 组和第k组含n个高斯白噪声的信号（n=1, 2, …）；E1(·)、Ek(·)分别为EMD 分解产生的1 阶和k阶模态分量；M(·)为信号的局部均值；r1、rk分别为第1 次和第k次分解信号产生的残差信号；I1、Ik分别为第1 次和第k次分解信号产生的IMF 分量；ω(n)为均值为0 的高斯白噪声；σ为两临近IMF 之间的标准差，作为迭代结束判据。

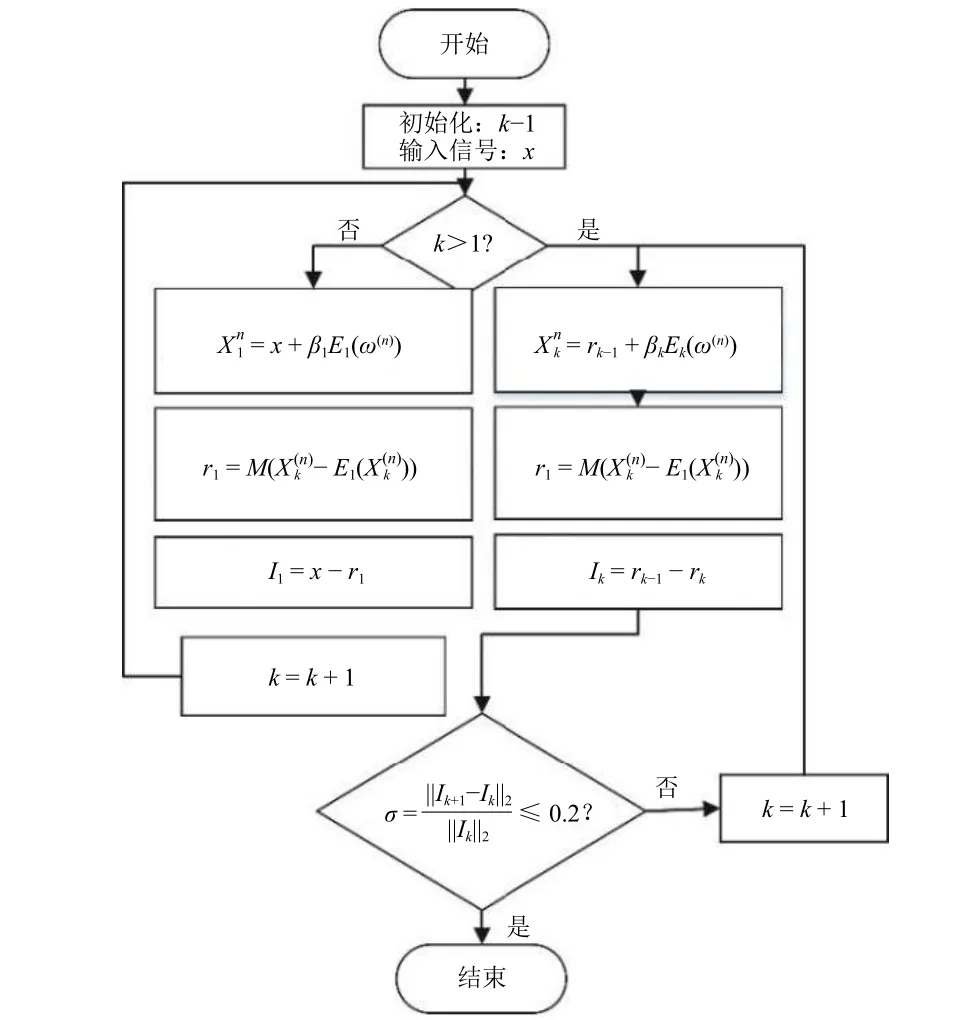
图1 ICEEMDAN 分解流程Fig.1 Flow chart of ICEEMDAN decomposition

1.2 PSO-MPE 特征提取方法

本文选取粒子群算法（PSO）优化的MPE 方法针对滚动轴承中的多尺度特征信号进行提取，其中MPE 的基本原理就是对信号进行粗粒化处理，而引入多尺度因子的MPE 方法能够对信号进行局部尺度上的信号粗粒化，更能反映信号的复杂性和随机性。MPE 的具体步骤可分为时间序列粗粒化、序列重构、概率计算和排列熵计算：

1）对原始信号进行多尺度粗粒化，令

式中：ys(j)为粗粒化后的数据排列；s为尺度因子。

2）序列重构，令

式中：l为重构分量；t为延迟时间；m为嵌入维数。

3）按升序排列，计算每一种符号序列出现的概率Pv；

4）排列熵计算，

式中HP为归一化后的多尺度排列熵。

由式(1)～式(4)可以看出：s值的选择直接影响多尺度特征提取的效果；而m的选择过大时会增加运算时间，过小时会造成重构信息不足；t的选择对时间序列的重构存在一定影响。因此，须引入PSO 针对MPE 中的这3 个参数进行寻优，以获得更好的信号特征提取效果。

1.3 CNN 分类方法

与传统的SVM 方法的线性分类方法不同，CNN因其特有的卷积操作、稀疏连接操作以及非线性函数激活操作对MPE 方法提取后的数值有着更为优秀的分类能力。滚动轴承信号为一维信号，因此本文选择一维卷积核进行网络构造，其网络结构如图2 所示，具体参数为：迭代次数200，mini-batch=4，初始学习率1×10-3，最小学习率1×10-8，通过Adam 方法进行参数优化，卷积激活函数为Relu，分类函数为Softmax。

图2 CNN 网络结构示意Fig.2 Network structure of CNN

2 信号分解和特征提取

2.1 用ICEEMDAN 进行信号分解

以美国凯斯西储大学开放轴承数据库样本[18]中12 Hz 采样频率下编号118 的保持架故障6000采集点信号为对象，通过ICEEMDAN 分解方法对其进行分解。首先，对原始信号进行分解，图3 为保持架故障信号的时域图，图4 为经过ICEEMDAN分解后的各IMF 分量时域图。然后，将各个IMF 分量同原始信号按

图3 原始信号时域图Fig.3 Time domain diagram of original signal

图4 ICEEMDAN 分解的IMF 分量时域图Fig.4 Time domain diagram of IMF component of ICEEMDAN decomposition

进行相关性计算，结果如表1 所示。最后，需选取那些强于弱相关的（即，相关系数＞0.2 的）IMF 分量进行重构。

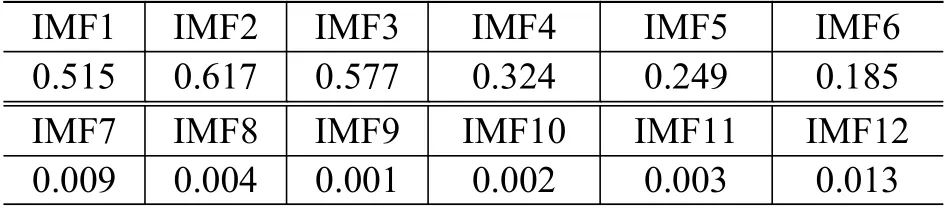
表1 各IMF 分量与原始信号的相关系数Table 1 Correlation coefficient of each IMF component and original signal

2.2 PSO-MPE 信号特征提取

以凯斯西储大学开放轴承数据库样本[18]中12 Hz采样频率下编号为105、130、118 和97 的4 类故障（分别为轴承内圈故障、轴承外圈故障、轴承保持架故障、正常）信号的ICEEMDAN 分解重构信号为对象进行PSO 寻优，对MPE 的参数进行优化，结果见表2。

表2 PSO 寻优的MPE 参数Table 2 MPE parameters of PSO optimization

从4 类故障信号中各选7 条（或12 条）数据分别进行PSO-MPE 特征提取和MPE 特征提取，PSO-MPE 参照表2 选择参数，结果按最少尺度因子的数量进行表示；MPE 的参数参照文献[19]选择s=12、m=6、t=1，结果按12 尺度因子的数量进行表示。两种方法的提取效果对比如图5 和图6 所示，从3D 图和2D 图都能够看出，经过PSO 优化后不同故障之间的MPE 值相差较大，表明经过PSO 优化后的MPE 能够使从各类故障中提取到的信号特征区分更明显，比单纯MPE 方法的特征提取效果更好。

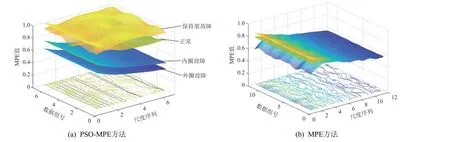
图5 PSO-MPE 与MPE 方法的提取效果3D 呈现Fig.5 3D rendering of extraction effect by PSO-MPE and MPE methods

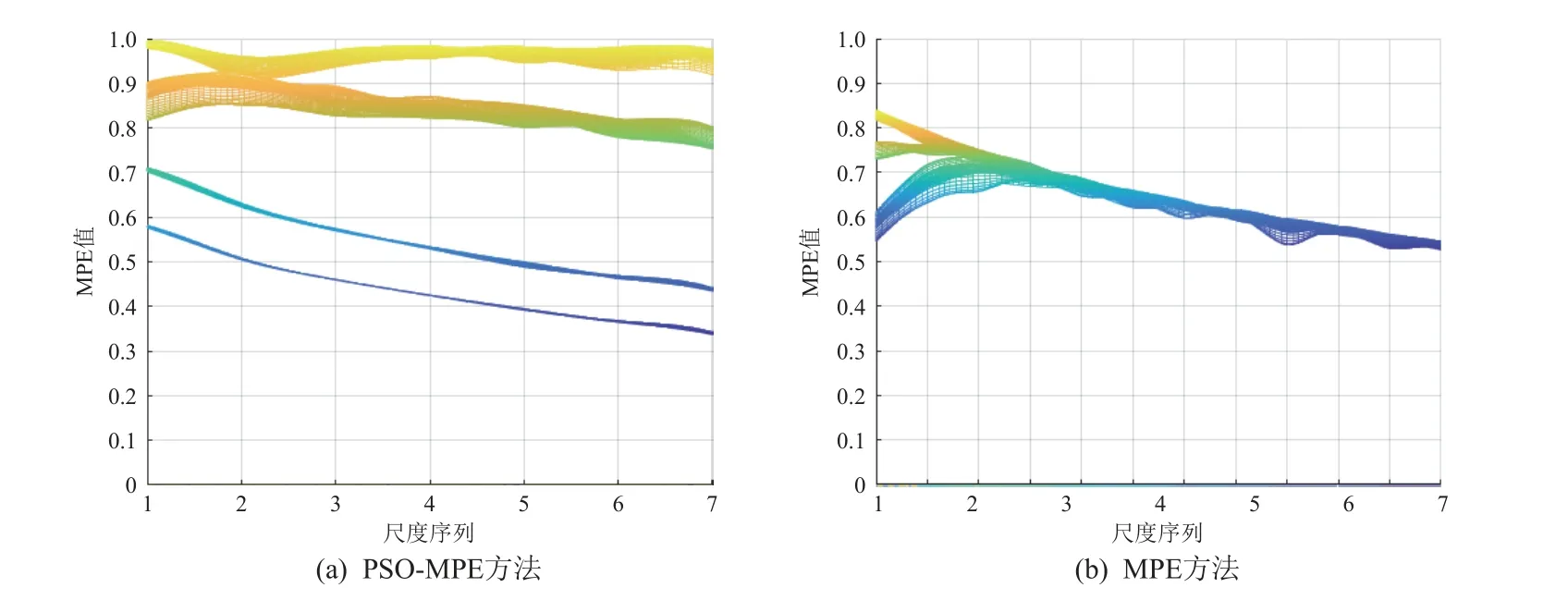
图6 PSO-MPE 与MPE 方法的提取效果2D 呈现Fig.6 2D rendering of extraction effect by PSO-MPE and MPE methods

3 实验与对比分析

3.1 实验平台和实验数据

本文使用的实验计算分析平台为戴尔Precision5820 系列服务器，操作系统为Ubuntu 18.04LTS，显卡为RTX3060Ti×2，CPU 为i9-10920X，显存16 GByte×2，深度学习框架搭建为Keras。

实验数据选自凯斯西储大学开放轴承数据库样本，总共960 条，其中480 条为训练数据集，160 条为验证数据集，320 条为测试数据集。

3.2 实验结果

用本文的ICEEMDAN-PSO-MPE-CNN 方法训练的准确率如图7 所示，可以看出，在20 多次迭代后，训练和验证的分类准确率逼近100%并处于收敛状态。

图7 本文方法的训练准确率Fig.7 Train accuracy of the proposed method

对本文方法的故障分析结果进行T-SNE 可视化，具体如图8 所示，图中不同颜色代表着不同故障种类降维后的结果，在通过ICEEMDAN-PSOMPE-CNN 分类后，相同颜色即相同故障会聚集，而不同故障会明显分开。可以看出不同故障类别之间有着明显的区分界限，这一结果直观地证明了该方法优秀的故障分类能力。

图8 本文方法故障分析结果的T-SNE 可视化Fig.8 T-SNE visualization of fault analysis results of the proposed method

3.3 实验对比分析

以测试集的数据为对象，进行纵向对比实验，将本文构建的ICEEMDAN-PSO-MPE-CNN 方法分别和ICEEMDAN-PSO-MPE-SVM、ICEEMDAN-MPESVM、MPE-SVM 方法进行对比，结果如表3 所示。通过分类结果正确识别的故障数据总数与测试样本总数的比值计算分类准确率，并以此作为不同方法的性能对比指标。

从表3 中可知，ICEEMDAN-MPE-SVM 的准确率比MPE-SVM 的高出21.88 个百分点，证明通过ICEEMDAN 分解重构后的信号使得分类的效果获得了极大的提升。ICEEMDAN-PSO-MPE-SVM的准确率比ICEEMDAN-MPE-SVM 的高出1.25 个百分点，表明PSO 对MPE 的参数优化能够使得提取到的不同故障特征区分度更大。ICEEMDANPSO-MPE-CNN 的准确率比ICEEMDAN-PSO-MPESVM 的高出1.87 个百分点，说明CNN 相对SVM 有着更强的分类能力，达到了100%的分类准确率。综上，最终获得的ICEEMDAN-PSO-MPE-CNN 方法相对最初的MPE-SVM 方法分类准确率提高了25 个百分点，证明了本文改进方法的可行性。

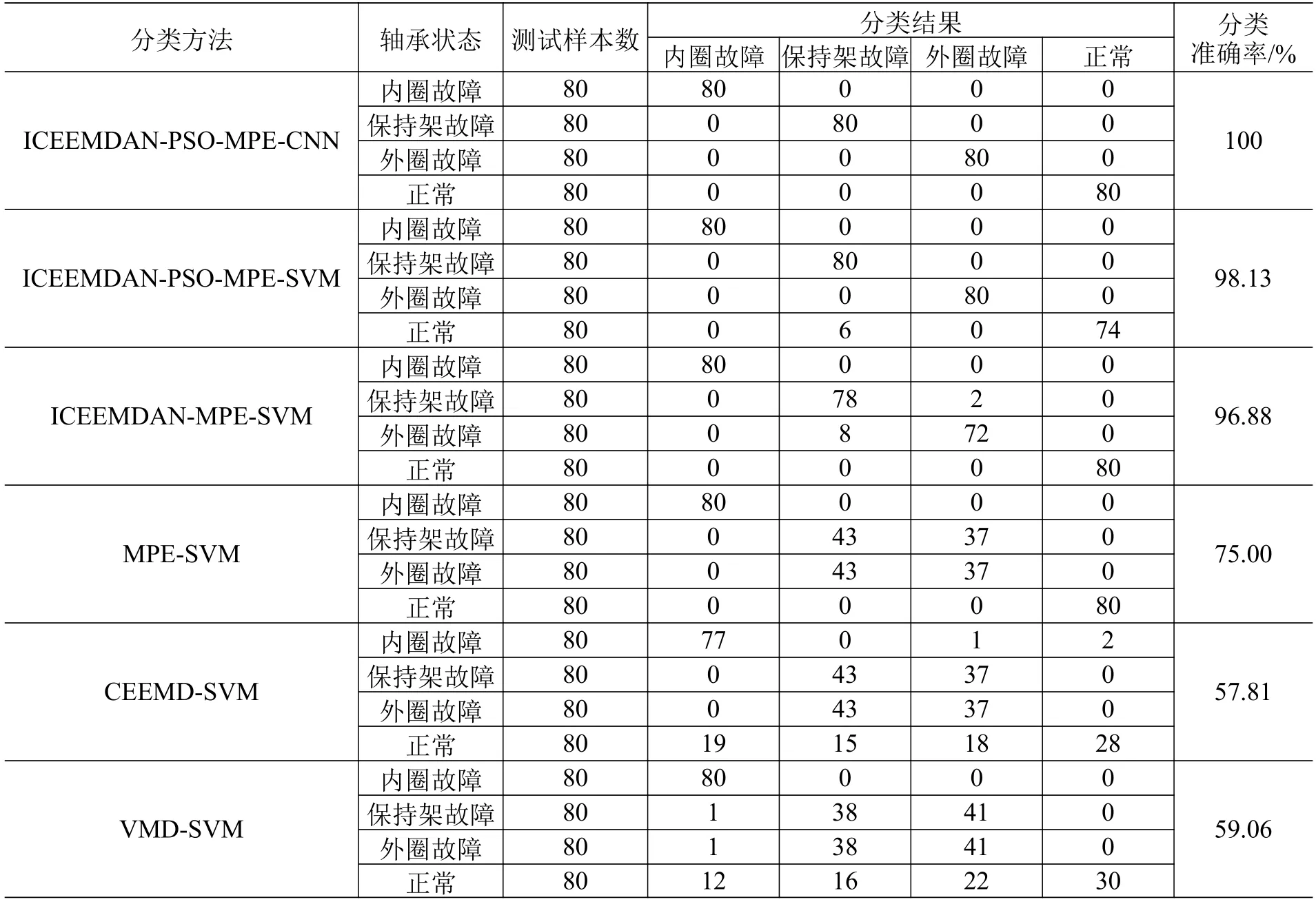
表3 几种故障诊断方法测试结果对比Table 3 Comparison of test results of several fault diagnosis methods

再以测试集的数据为对象，进行横向对比实验，将本文构建的ICEEMDAN-PSO-MPE-CNN 方法分别和CEEMD-SVM、VMD-SVM 方法进行对比，结果同见表3。从表中可以看到，ICEEMDAN-PSOMPE-CNN 方法相对CEEMD-SVM 和VMD-SVM方法的分类准确率分别提高42.19 和40.94 个百分点，证明了本文方法相对一些经典滚动轴承故障诊断方法的优越性。表3 显示，MPE-SVM、CEEMDSVM 和VMD-SVM 在识别分类外圈故障和保持架故障时出现了相互识别错误的结果，说明这些方法没能同时完成分解降噪和特征提取的工作，在数据提取后这2 种故障类别的数据依然存在严重的非线性分布，故通过非线性数据处理能力较差的SVM难以实现很好的分类识别。

为证明用CNN 作为序列预测方法的合理性，将ICEEMDAN-PSO-MPE-CNN 同ICEEMDAN-PSOMPE-RNN 和ICEEMDAN-PSO-MPE-Transformer 进行对比，结果如表4 所示。从表中可知，应用CNN、RNN、Transformer 作为序列预测的方法都能获得100%的检测准确率，这一定程度上也证明了PSOMPE 特征提取方法的优越性。但是，对比参数量，CNN 相较于后两者分别少了16 384 和2 600 782；对比训练时间，CNN 相较于后两者分别缩短3 ms/step和2 ms/step；对比测试时间，CNN 相较于后两者分别缩短24.07 s 和9.50 s。可见虽然应用CNN、RNN、Transformer 对于本文选取的案例都能够获得100%的检测准确率，但是CNN 方法能够在参数量更少的情况下实现更高效率的训练和检测。

表4 三种序列预测方法的效率对比Table 4 Efficiency comparison of three sequence prediction methods

本文方法得到的故障预测精度大幅提升的主要原因是：ICEEMDAN 分解信号减少了信号中的不相关噪声信号，使得重构后的信号更容易进行特征提取；PSO 优化后的MPE 能够更好地把握信号中的多尺度特征，并对关键特征进行提取；通过非线性分类能力强的CNN 能够完成高准确率、高效率的故障诊断。

4 结束语

本文针对滚动轴承振动信号的特征信号微弱、信号非线性及多尺度特征难提取的问题，提出了基于优化多尺度排列熵和卷积神经网络的滚动轴承故障诊断方法。首先通过改进的CEEMDAN 将滚动轴承原始信号分解成包含各类模态特征的IMF，并进行相关性计算后再进行信号重构，以解决信号非线性和特征微弱的问题；其次提出利用多尺度排列熵提取信号特征的方法，并通过PSO 对MPE 进行参数优化；最后通过CNN 深度学习的方法对提取出来的特征进行分类。将本文方法与经典滚动轴承故障诊断方法分别进行纵向和横向的对比表明，本文方法具有更佳的分类准确率和更高效率，能够满足滚动轴承故障诊断对准确率的要求，具有较大的实际应用价值。而且，由于该方法有效实现了原始振动信号的降噪和非线性多尺度特征提取的过程，对于振动信号含噪声明显且包含多尺度特征的齿轮箱和航空发动机转子同样适用，有较大的应用前景。