基于GI-AMED的滚动轴承早期故障诊断

崔奔，郭盼盼，张文斌

(1.昆明理工大学 机电工程学院，昆明 650500；2.红河学院 云南省高校高原机械性能分析与优化省重点实验室，云南 蒙自 661199)

滚动轴承是机械设备中应用广泛的部件，也是极易损坏的部件，其运行状况直接影响整个旋转机械设备的稳定性，对滚动轴承进行健康状态评估和早期故障诊断具有十分重要的意义[1]。滚动轴承发生故障时会产生一系列的周期性脉冲，从被噪声污染的振动信号中提取脉冲特征是轴承故障诊断的关键步骤[2-3]。

最小熵解卷积(Minimum Entropy Deconvolution，MED)于2007年首次应用于轴承与齿轮的故障诊断[4-5]，国内学者陆续将其与稀疏分解[6]、变分模态分解[7]、支持向量机[8]、联合平方包络谱[9]等方法相结合，用于滚动轴承微弱故障特征的提取和分类。最小熵解卷积通过最大化轴承振动信号中冲击分量的峭度值并最小化其他噪声分量的峭度值[3]实现故障信号的降噪并突出冲击成分，其降噪效果取决于滤波器长度的选取。模糊熵是一种可以表征信号复杂程度的熵[10]，轴承振动信号经最小熵解卷积降噪后，周期性脉冲成分与噪声成分分离，信号由无序变有序，模糊熵值也由大变小，可将模糊熵作为标准实现最小熵解卷积参数的自适应选取。

基尼系数[11]是经济学中用来衡量收入分配均匀程度的指标，滚动轴承振动状态出现异常时，监测信号呈现的稀疏性与经济学中描述居民收入分配的不均衡性相似。因此，本文将基尼系数用于处理轴承退化数据，判断轴承产生早期故障的时间范围；并采用自适应最小熵解卷积进行降噪预处理，通过包络解调实现轴承故障特征的提取。

1 理论分析

1.1 最小熵解卷积

最小熵解卷积的实质是通过解卷积的计算过程寻找最优逆传递函数，并作用于输入信号，以此恢复信号中的冲击脉冲[12]。滚动轴承的振动信号y(n)可以表示为

y(n)=h(n)*x(n)+e(n)，

(1)

则

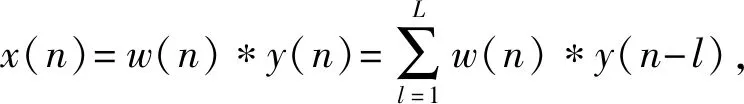
(2)

式中：x(n)为冲击信号；h(n)为传递函数；e(n)为噪声成分；w(n)为最优逆传递函数；L为逆滤波器的长度。

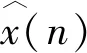
(3)

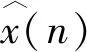
(4)

则

(5)

(6)

式中：b为y(n)和x(n)的互相关矩阵；A为y(n)的自相关矩阵。

最小熵解卷积的算法可以归纳如下[12]：

1)初始化w(0)中的元素全为0；

2)迭代计算x(n)=w(n)i-1*y(n)；

3)计算b(i)(l)；

4)计算w(i)=A-1b(i)；

1.2 模糊熵

模糊熵用于描述时间序列的复杂度，广泛应用于机械设备的故障诊断领域[13]。对于时间序列X={X1,X2,…,XN}，构造m维向量X(i)=[Xi,Xi+1,…,Xi+m-1]，其中1≤i≤N-m。则X(i)，X(j)对应元素之差中绝对值的最大值为

(7)

借助模糊隶属度函数测量向量X(i)，X(j)之间的相似程度。模糊隶属度函数为

(8)

则互相关概率的平均值为

(9)

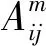
对于维数m+1，迭代(7)—(9)式可得到Bm+1(r)，则模糊熵可表示为

EFE(m,r,N)=lnBm(r)-lnBm+1(r)，

(10)

本文选取模糊熵的维数m=2，相似容限r=0.2[14]。

1.3 基尼系数

当滚动轴承出现故障时，其振动信号的能量通常集中在信号序列的某些位置，故障信号呈现出的稀疏性与经济学中描述居民收入分配的不均衡性很类似，因此可利用基尼系数表征滚动轴承故障的发展趋势并进行健康状态评估。对于时间序列X={X1,X2,…,XN}，向量Xi为

(11)

则基尼系数可表示为

(12)

式中：A为时间序列的正序排列；F为时间序列的和；基尼系数G的取值范围为[0，1]。

1.4 诊断步骤

最小熵解卷积的参数优化流程如图1所示，滤波器长度L的取值范围为2～300，将原始振动信号输入最小熵解卷积中进行优化，得到最佳L并获得自适应最小熵解卷积。将原始振动信号输入自适应最小熵解卷积中进行降噪处理，然后经过包络解调提取出故障特征频率，具体诊断流程如图2所示。

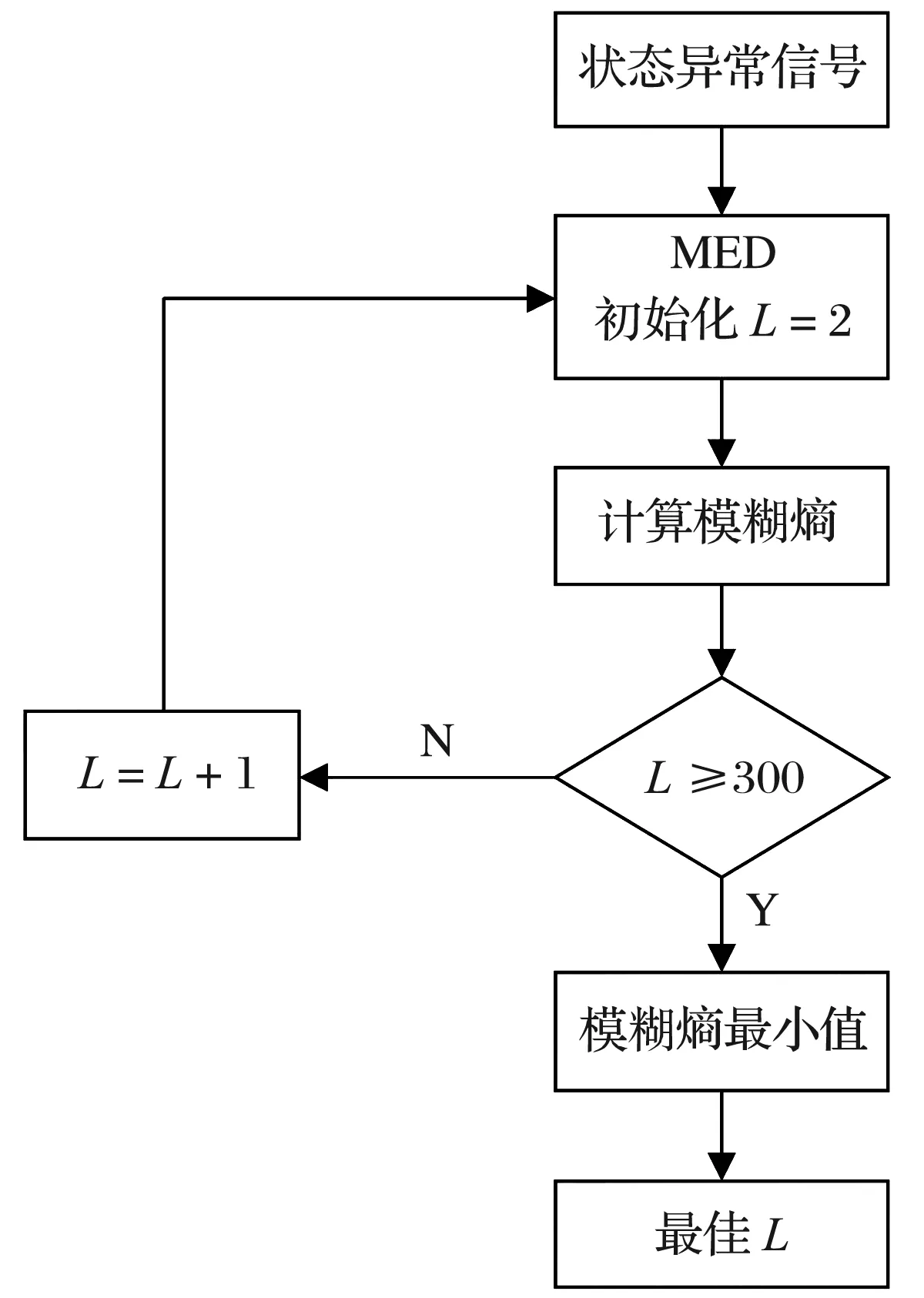
图1 MED参数优化流程图Fig.1 Flow chart of MED parameter optimization

图2 基于GI-AMED的滚动轴承故障诊断流程Fig.2 Fault diagnosis process of rolling bearing based on GI-AMED

2 试验分析

采用美国辛辛那提智能维护中心的滚动轴承全寿命数据[15]进行分析，试验台结构如图3所示，轴承与电动机通过皮带连接，每套轴承的水平和垂直方向各放置一个加速度传感器采集数据。试验轴承型号为ZA-2115，转速为2 000 r/min，具体参数见表1。选用发生外圈故障的1#轴承的数据进行分析，每10 min采集一次数据，共得到984个数据。

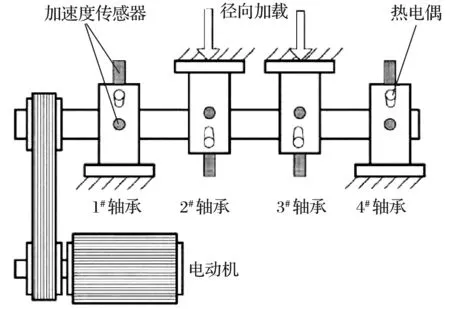
图3 试验台结构示意图Fig.3 Structure diagram of test bench

表1 ZA-2115轴承的基本参数Tab.1 Basic parameters of ZA-2115 bearing

1#轴承全寿命周期的运行趋势如图4所示：在7 020 min时均方根值有明显突变，表明轴承发生了故障[13]；基尼系数则从5 280 min开始有上升趋势，在7 020 min发生了更明显的突变，判断轴承产生故障；采用最小二乘法对轴承运行状态开始变化的上升沿数据进行直线拟合，通过直线斜率K的对比可以看出，相对于均方根值，基尼系数对滚动轴承运行状态的变化更敏感。

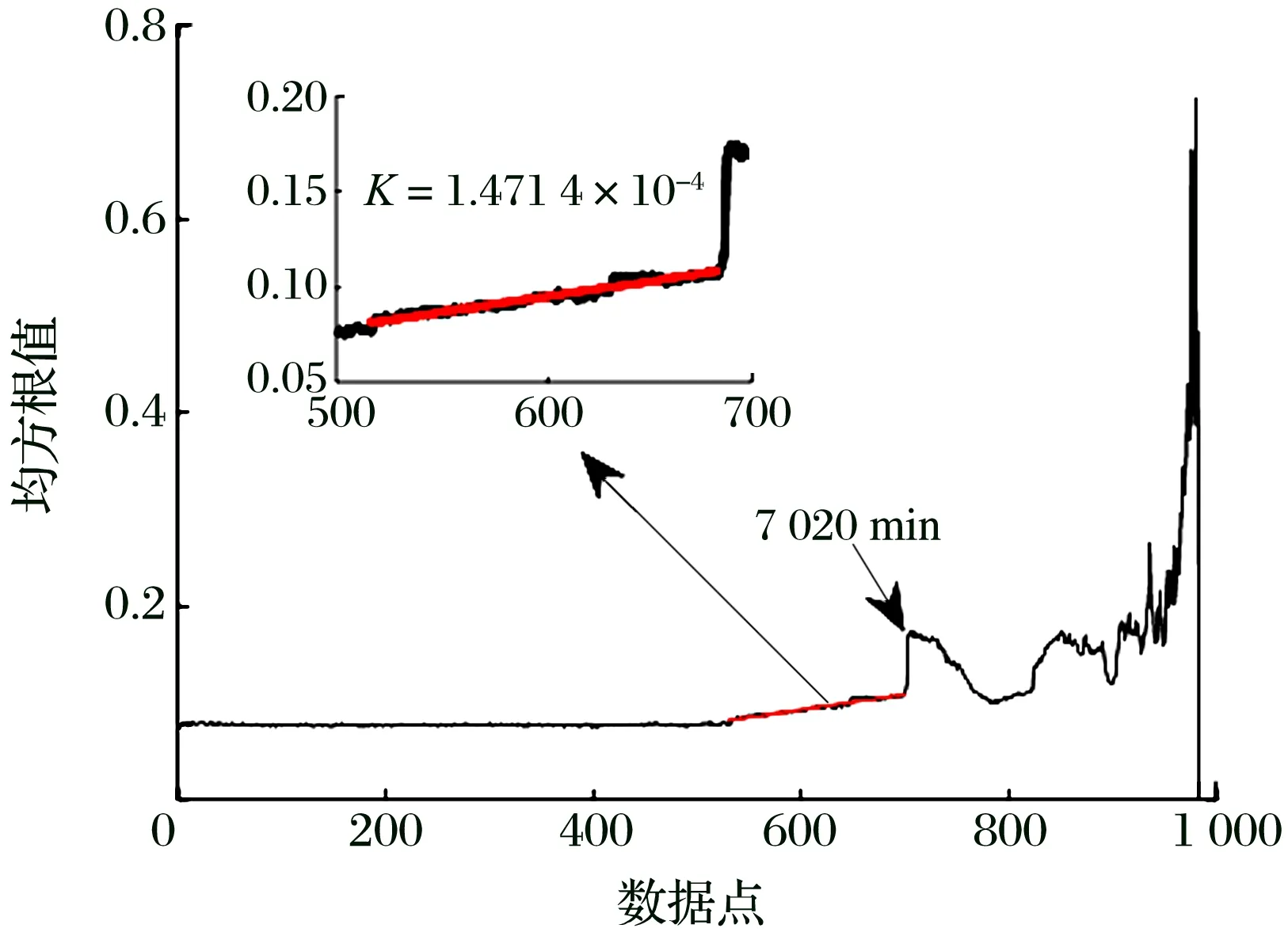
(a) 均方根值

为验证GI-AMED对轴承早期故障诊断的有效性，选取轴承状态初始变化点(5 280 min)的振动数据进行分析，该时刻轴承振动信号的时域波形及其包络谱如图5所示，包络谱中存在较多干扰成分，观察不到明显的故障特征频率。

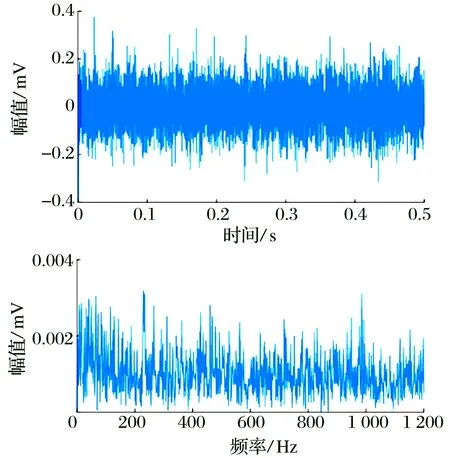
图5 第5 280 min轴承振动信号的时域波形与包络谱Fig.5 Time-domain waveform and envelope spectrum of bearing vibration signals at 5 280 min

采用GI-AMED对第5 280 min轴承振动信号进行处理，通过模糊熵对最小熵解卷积的参数寻优结果如图6所示，利用AMED对轴承振动信号进行降噪处理的结果如图7所示：从包络谱中可以观察到明显的外圈故障特征频率(230 Hz)及其倍频，与发生明显突变的第7 020 min相比提前了1 740 min实现轴承早期故障诊断。

图6 AMED滤波器长度L的寻优结果Fig.6 Optimization result of AMED filter length L

图7 AMED降噪后的时域波形与包络谱Fig.7 Time-domain waveform and envelope spectrum after AMED noise reduction

作为对比，文献[7]采用最小熵解卷积与变分模态分解对5 370 min的轴承振动数据进行分析(图8)，其依靠经验选取MED滤波器长度L为79，直接进行包络谱分析后只能识别故障特征频率，但倍频被干扰谐波淹没，对降噪信号进行变分模态分解后以峭度值为标准选取最优分量进行包络谱分析才能识别出倍频。而GI-AMED只需进行包络谱分析就可提取出故障特征频率及其倍频，且所处理数据提前了90 min采集，故障特征更加微弱，充分说明了本文所提方法在滚动轴承早期故障诊断中更具优越性。

图8 文献[7]最优分量IMF3的包络谱Fig.8 Envelope spectrum of optimal component IMF3 in reference [7]

3 结束语

均方根值是轴承运行趋势常用的统计指标，本文利用经济学中的基尼系数对轴承全寿命周期数据进行处理，与均方根值拟合直线斜率的定量对比证实了基尼系数是一种更优越的指标。利用模糊熵对最小熵解卷积的参数L进行寻优，克服了人为经验选取的局限性，对比分析结果也表明其降噪效果更好，GI-AMED方法能够更好地实现滚动轴承早期微弱故障的有效判定。