牵引力控制对列车乘坐舒适度的影响研究

王景琪，李 鹏，彭志勇，王 雪，李昭孟

应用研究

牵引力控制对列车乘坐舒适度的影响研究

王景琪1，李 鹏2, 3，彭志勇4，王 雪5，李昭孟5

（1. 中车大连机车车辆有限公司，辽宁大连 116021；2. 株洲中车时代电气股份有限公司，湖南株洲 412001；3. 西南交通大学，成都 610036；4. 广州机车检修段，广州 510000；5. 中国铁路沈阳局集团，沈阳 110000）

列车乘坐舒适度本质是多体运动学问题，量化评估需同时获取列车横-纵-垂三个维度的振动信息。因此，在进行列车乘坐舒适性优化研究时通常需要实车实验，这极大的制约了优化迭代效率。为了解决该问题，本文首先使用SIMPACK对列车的轮轨关系、转向架一系二系悬挂、车体以及钩缓装置等进行了建模，并分析了基于列车三维振动信息的乘坐舒适性评价理论下不同速度对舒适度影响。通过对比不同控制策略下的列车动力学情况，并按舒适度理论对其量化，发现优化牵引力加载策略能有效提高舒适度，相比于传统的实车试验，本文提出的多体动力学仿真方法能有效改善舒适度优化成本与效率，通过优化牵引控制来提升乘坐舒适度有着重要意义。

动力学仿真 乘坐舒适性 舒适度量化评估 牵引力控制策略

0 引言

近年来，由于轨道交通列车具有运行准时、安全平稳、方便换乘、性价比高等优点，使其成为市民日常通勤的首选交通方式。随着社会生活水平的不断提高，人们乘坐城市轨道列车出行时不仅追求快速和安全，而且更加注重出行时的舒适性。越来越多的城市地铁招标文件对列车乘坐舒适度提出了更高要求。

列车旅客的乘坐舒适度，一般可通过车辆多维振动信息来量化评价,列车振动状态又受轨面状况、列车转向架结构、车体之间的钩缓装置以及列车牵引状态等多种因素影响。在上述影响因素中，对于已投入运营的线路及车辆而言，其轨面状态与列车机械结构都难以进行针对性优化，只有列车牵引状态可以通过控制策略对其进行优化提升，以改善列车运行时的振动状态。因此，研究列车牵引控制对乘坐舒适度的影响，能有效改善乘客的乘坐体验。

1 列车动力学模型的简化与建立

1.1 列车建模动力学基本参数

本文基于多体动力学软件SIMPACK[1]对列车的舒适度进行建模仿真分析。该模型为四轴动力车，转向架采用B0-B0结构型式。车体模型包括轮对，轨道、转向架、一系悬架、二系悬架、轴承鞍、上车体等。其中一系悬挂中的垂向减振器对缓冲车轮和构架间冲击振动有着重要的作用。二系悬挂由蛇形、横向减震器以及空气弹簧组成，对缓和车体横向的冲击振动有着重要作用。车辆模型中的其他结构参数详见下表。

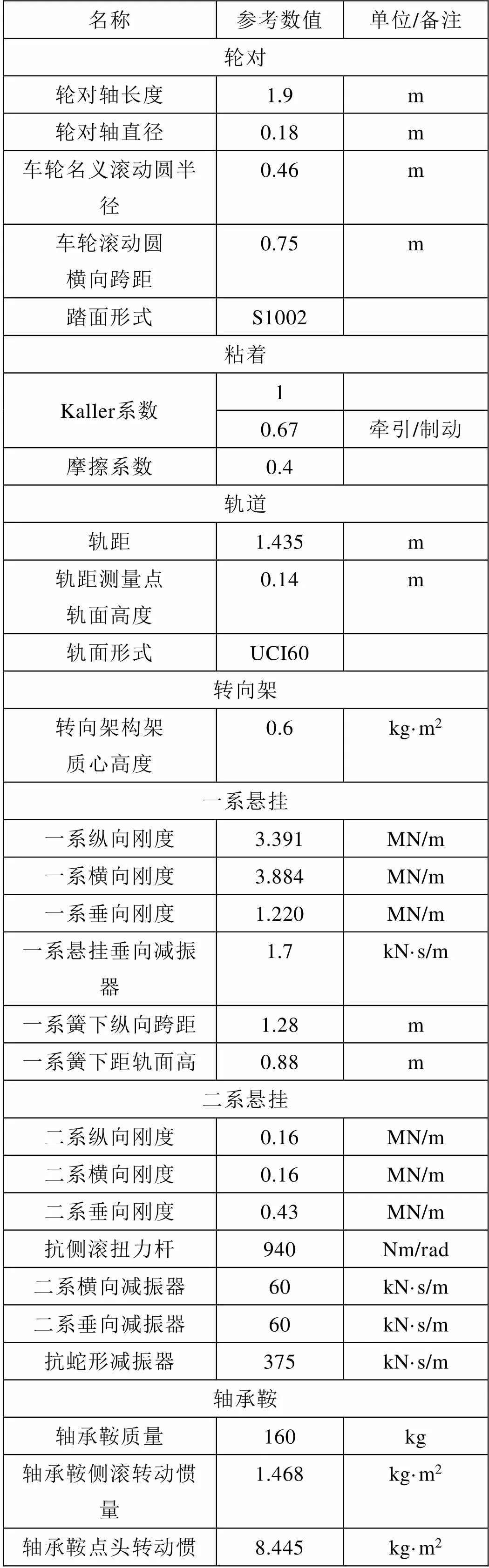
表1 转向架和车体的结构参数表

车辆是一个复杂的多体动力学系统，各个零件均可发生相互作用。如果对整车进行建模，不仅仅工作量巨大，也会使得模型极其复杂，仿真效率得不到有效保证。故本文在建模时，力求保证动力学性能的情况下，聚焦重点的建模要素[2][3]。根据车辆本身的结构特点、各个结构件的参数，本文将模型简化轮轨-转向架-上车体的离散多体动力学系统。重点考虑转向架各个联结零件所发挥的减振作用。

基于上述因素，本模型在建立过程做了如下考虑：

1）列车动力学性能的主要影响因素为两系悬挂，而车体、轴箱等零部件产生的变形很小，可以忽略不计。故将这些零部件视为刚体。

2）列车牵引制动工况中，通过Matlab函数的方式控制电机力矩。这个力矩直接施加在仿真模型的动轴上。

3）不考虑铁轨和道床的相互作用，不考虑铁轨本身的振动，视轨道整体为刚体。通过在轨道上施加外部激励来模拟轨道在垂向和横向上的空间误差。

1.2 车辆拓扑结构

以轨-轮-架-车的离散的多体动力学建模思路，在SIMPACK中分别建立轨道、转向架、上车体的中各个子部件，将所有子部件进行装配。最后将装配而成的整体模型进行静平衡操作。

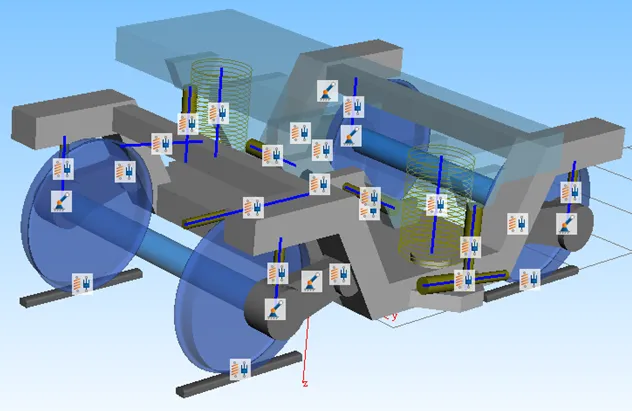
图1 转向架三维图

轮对模型中的弹簧等均设定为无质量的联结单元，其数值参考表1。图1为转向架三维图，其中建立刚度阻尼力元来模拟空气弹簧，刚体形式的轴箱用来约束横、纵两个方向的位移。

1.3 轨道不平顺

Simpack仿真模型中的默认轨道模型均为理想轨道，但实际轨道在垂向和横向上都与理想值误差较大。这种空间误差称之为轨道不平顺[4][5]，它使车辆受迫运动，造成不规律的机械振动，这种振动经过悬架过滤传递到乘坐空间从而影响乘坐列车乘坐舒适性。国外通过深入研究和大量的实地测量分析轨面，得到一些业界认可的轨道谱。目前比较常见的轨道不平顺谱为美国谱、德国谱。我国城市轨道交通路况条件与德国的低干扰谱拟合路况更接近。为模拟接近真实路况，本文将德国低干扰谱施加在轨道模型上。

其轨道垂向不顺的表达式为：

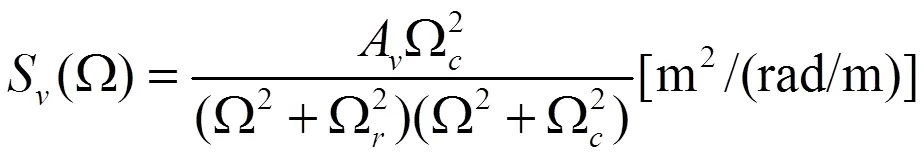
轨道横向不平顺表达式为：

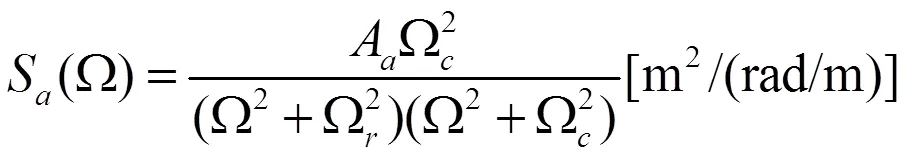
式中，()为功率谱密度；为空间频率；A、A为粗糙度；Ω、Ω截断频率。

式（1）和式（2）中的粗糙度和截止频率取值为：Ω=0.8246，Ω=0.0206，Ω=0.4380，A=2.119e-7，A=4.032e-7

本文的研究工况主要为直线工况。在多体动力学软件SIMPACK中，将德国轨面低干扰谱加在轨面单元上。其横向和垂向不平顺如图2与图3所示。

图2 横向不平顺

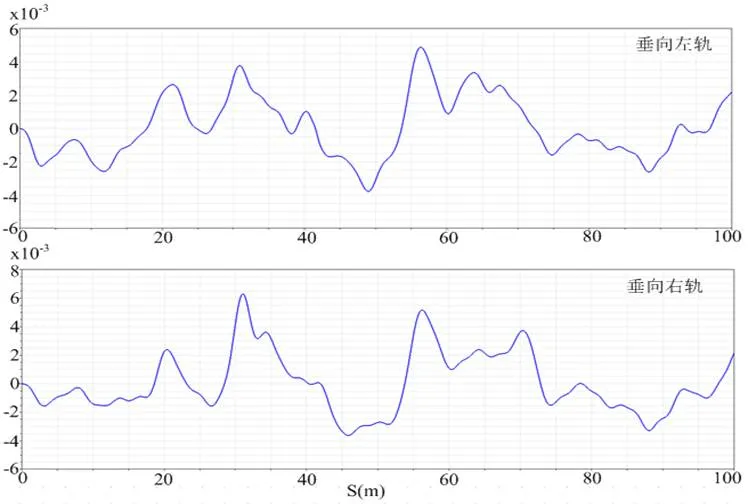
图3 垂向不平顺

2 舒适度分析

2.1 车辆舒适度评价理论

列车作为一个复杂的多体动力学系统，横-纵-垂三向之间存在动力学耦合关系，由于轨面本身的不平顺或牵引制动引起的各向加速度通过车体、一二系悬挂、轮轨、车钩联结等环节传递至车厢内。这种冲击振动对乘坐舒适性的影响最大，故本文的舒适性分析是基于列车各向加速度。本文介绍两种基于加速度的舒适度分析理论：第一种是基于列车车厢地板处加速度值，其中TB/T 2360-93和GB5599-853[6]标准根据车辆加速度极值对舒适的分级，，但是该评价方法较为机械僵硬。第二种是更注重乘客的主观感知敏感程度Sperling舒适度评价理论[7]。该理论采集了大量的列车走行数据对各个维度的加速度值和频率通过加权来综合评价。本文通过舒适度评价理论的指标对列车乘坐舒适这种主观感受进行量化评估，把多体动力学仿真研究牵引力控制对列车舒适度的影响分析环节进行闭环。

1）车体加速度指标

对于客车车体，可根据GB5599-853标准，当其速度≦140 km/h时，其公式如下：

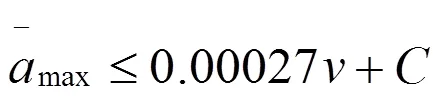
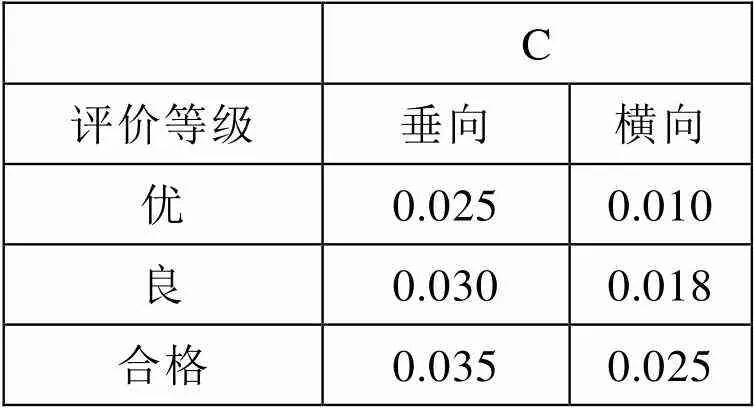
表2 计算常数

对于司机室舒适度评价，可依据TB/T 2360-93标准：

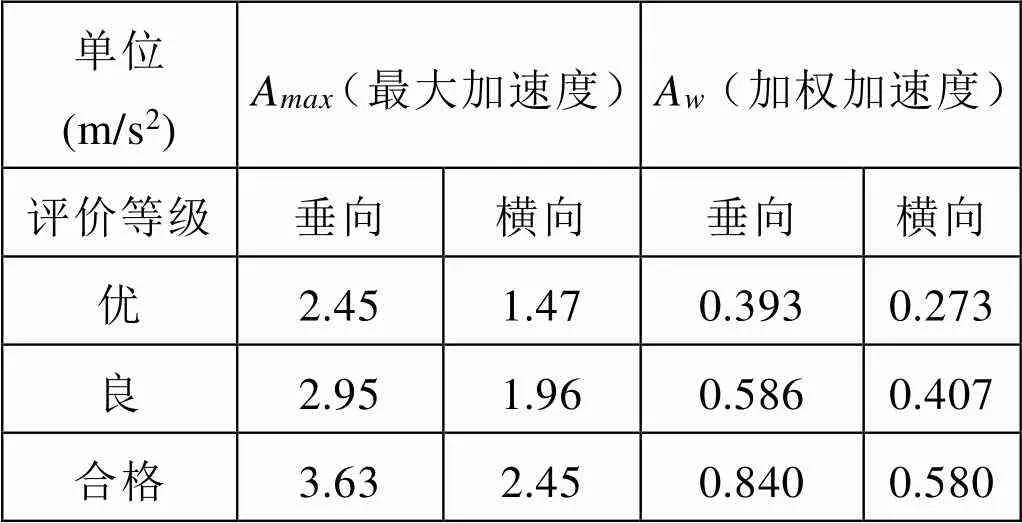
表3 列车加速度评价标准

其中，AA根据垂向和横向振动幅值将舒适度评级分为优、良、合格。

2）Sperling-W指标

Sperling理论是国际上用来评价列车走行平稳性和乘员乘坐舒适性最为认可和运用最为广泛。Sperling舒适度值用来表示，计算公式如下：

用于运行品质的评价：

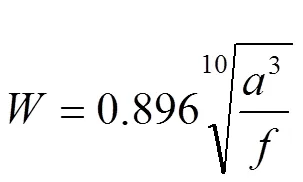
用于舒适度的评价：

式中，为振动加速度(m/s)；为振动频率；为加权系数，和列车振动频率有关，在横向和垂向上，加权系数的值是不一样的，具体加权系数如表4所示。

由于在轨道模型上施加了干扰谱激励函数，所以列车走行产生振动传递到车厢内，乘客感受到的加速度也具有随机性。故根据频率值范围对加速度进行分类并计算值。

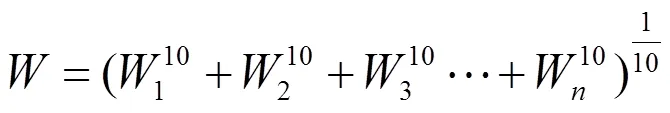
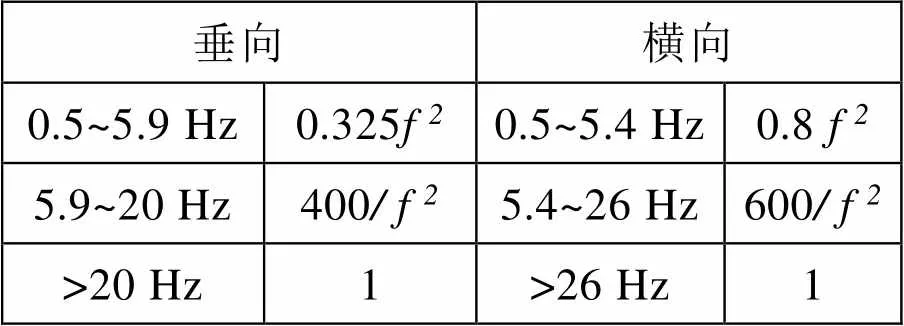
表4 频率加权系数表

经过，人体对横-纵-垂三向振动的主观感受统一到Sperling值来评价舒适度，列车的走行平稳性和乘客乘坐的舒适度对应关系[8]如下表所示。

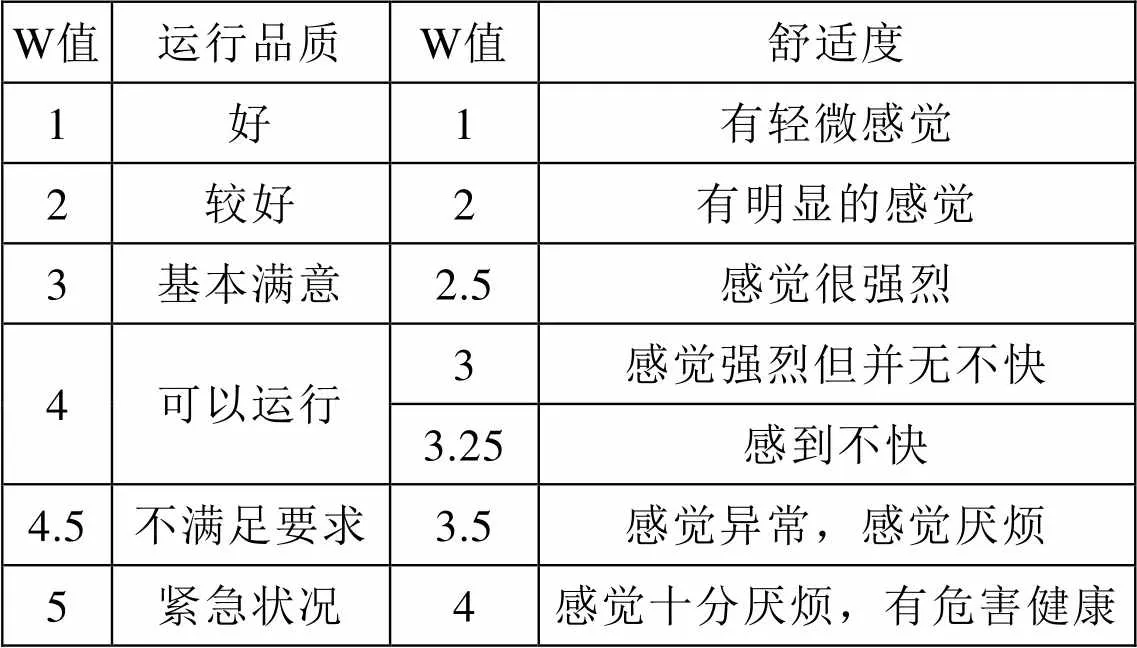
表5 列车平稳性及舒适度评价指标

2.2 车辆速度对舒适度的影响

对四轴动力车设计了三个速度工况：分别是40 km/h，60 km/h，80 km/h。轨道线路总长10000 m，激励路面从10 m处开始，50 m的过渡路段。其工况表如下表所示：

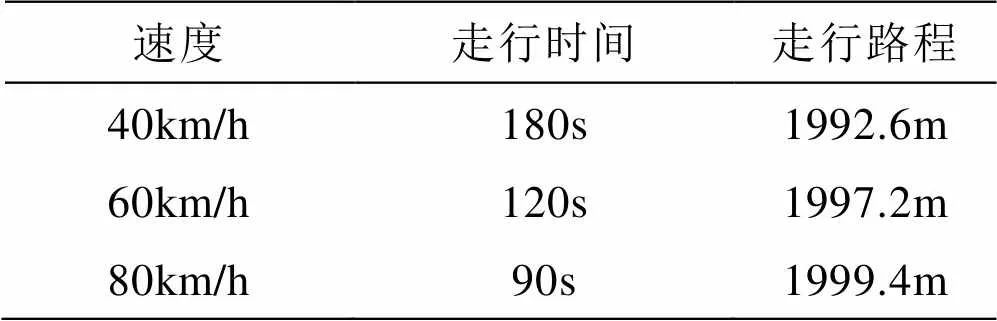
表6 不同速度工况表

从上表可以知设定不同时长的计算时间是为了保证车辆走行过激励路面长度相近。

为了提取车辆横向和垂向的加速度，在车体重心处增加了传感器单元，通过SIMPACK后处理软件得出如图4所示加速度波形。

对加速度数据进行分析后处理后，得出不同速度的Sperling值，如表7所示。

图4 不同速度下的横向、垂向加速度图

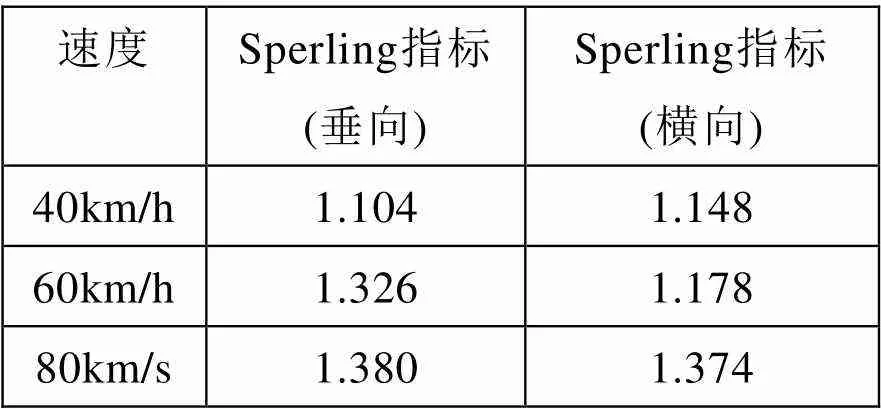
表7 不同速度的Sperling-W值

由于本文选取的路面激励为德国低干扰谱，轨道路况较好。所以舒适度指标Sperling-W值均在较为舒适区间。随着列车走行速度变大，通过观察舒适度指标Sperling-W值可以发现中低速（40 km/h到60 km/h区间）垂向舒适度变化更为敏感，而中高速（60 km/h到80 km/h区间）横向舒适度变化更为敏感。

2.3 列车牵引力矩加载速率对舒适度的影响

为了使模型更接近真实工况，在模型中加入无动力的拖车车辆，车体之间用车钩单元连接。为了模拟牵引力矩加载对车体运动的动力学变化的影响，此处采用Simlimk/Simpack[9]联合仿真，使用Matlab模拟列车牵引时动力轴力矩的加载函数，将该力矩以函数形式输入Simpack对应的四根动力轴上，最后输出轮对角速度，以得到车体运动情况。（a）力矩中断后，0.2s内恢复（b）力矩中断后，0.8 s内恢复。（c）力矩中断后，0.2s内恢复（d）力矩中断后，0.8s内恢复（e）力矩中断后，7s恢复（f）力矩加载平稳后，中断2s后恢复。

为研究牵引力加载因素的影响，设定初始速度为50 km/h，并将动轴上的目标加载力矩均设定为25 kNm，选取图5中的6个斜率牵引控制策略进行联合仿真，其仿真结果如图6所示。

在牵引力矩加载控制策略（f）中列车当15秒时瞬间切断牵引力矩，并持续2 s无力矩输入。此时列车瞬间失去动力进入惰性状态，而在17 s时迅速在0.2 s内恒定斜率迅速恢复到目标加载力矩。由于2秒的惰性车厢间车钩力的拉压状态复杂变化并且传递过程不均匀不同步，相比同样0.2 s内恢复的（a）工况，纵向加速度在23 s、26 s、28 s时出现较大的波动。

图5 牵引力加载工况

而工况(a)、(b)、(c)、(d)、(e)里，均是恒力矩加载在15 s切断牵引后又以不同的斜率恢复牵引力矩。通过对比(a)、(b)、(c)三种工况，可以发现：由于恢复力矩时斜率大，恢复速度快。三种工况的纵向振动收敛不柔和，并在收敛后出现再次较大短时波动。在(d)、(e)两种工况的纵向振动都在加载时间柔和收敛在后续并未引起纵向振动的短时波动。

不同牵引策略下的垂向振动加速度如下图7所示。

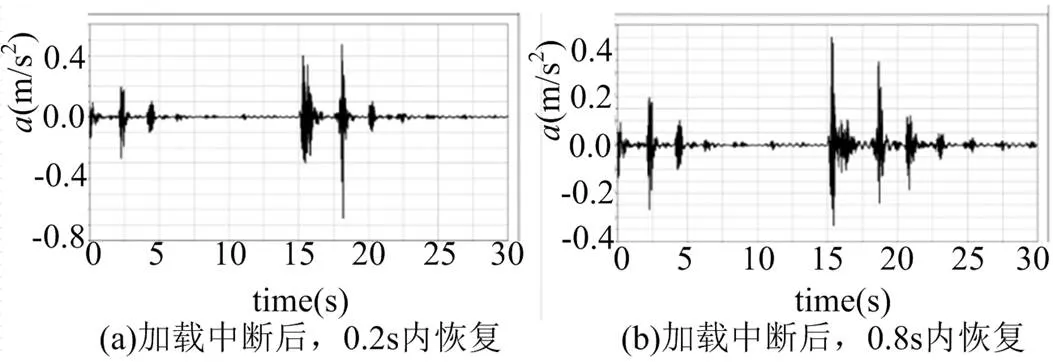
通过对比垂向、纵向振动可以发现，两种振动发生均和车钩力的状态迅速变化所导致的冲击有关。如表8所示：恢复斜率过快会导致加速度收敛不柔并引起短时冲击。当斜率小于一定值后，随着牵引力矩加载斜率变小，加速度收敛更为柔和。

表8 各个工况17秒后的舒适度指标

综合观察各个工况下车体的横向、纵向冲击振动变化可以发现：当突然切断牵引力会引起较大的冲击振动，在阻力作用下各个车体间的车钩力状态迅速发生变化，其拉应力变为压应力所导致的车体间冲击。当牵引的力矩恢复后，车钩力状态又发生改变，再次引起车体间冲击振动。同时，当牵引力矩加载速率恢复过快时，由于各个车体间的车钩力传递不均匀从而引起纵向、垂向上比较大的波动幅值。当恢复牵引力矩的加载速率变小时，波动幅值收敛柔和。随着牵引力矩加载的斜率变小可以有效降低Sperling值，以达到改善列车乘客舒适度。

3 结语

随着城市轨道交通的高速发展，人们对乘坐舒适度期望要求进一步提高。为研究列车牵引力控制策略对乘客乘坐列车的感知舒适度的影响，本文基于软件Simpack构建了车-架-轮-轨的动力学模型，并引入基于频域分析的Sperling舒适度理论对乘坐主观舒适度进行量化分析，从而进一步分析牵引控制策略对其的影响，发现在列车本身的动力学性能基础上进一步优化牵引力加载策略能有效提高舒适度。相比于传统的实车试验，本文提出的多体动力学仿真方法能有力的改善舒适度优化成本与效率，为面向乘坐舒适性的列车牵引控制优化提供了有效研究手段。

[1] 缪炳荣, 方向华, 傅秀通. SIMPACK动力学分析基础教程[M]. 西南交通大学出版社,2008.

[2] 罗仁, 曾京, 戴焕云. 列车系统建模及运行平稳性分析[J]. 中国铁道科学, 2006, 27(01):72-77.

[3] 张雯娣，颉方正. 一系悬挂参数对车辆动力学性能的影响[J]. 机械研究及应用, 2015, 28(03):91-92.

[4] 陈宪麦, 王澜, 陶夏新, 等. 我国干线铁路通用轨道谱的研究[J]. 中国铁道科学, 2008, 29(03):73-77.

[5] 钱雪军. 轨道不平顺的时域模拟法[J]. 铁道学报, 2000, 22(04): 94-98.

[6] 中华人民共和国. 机车车辆动力学性能评定及试验鉴定规范: GB/T 5599-2019[S]. 2019.

[7] 王悦明, 王新锐. 客车舒适度的评定[J]. 铁道机车车辆, 2000, (3): 1-4.

[8] 虞名扬. 高速列车多车编组动力学及动力舒适性研究[D]. 大连交通大学, 2018.

[9] 石良臣. MATLAB/Simulink系统仿真超级学习手册[M]. 人民邮电出版社, 2014.

Research on the influence of traction control on train ride comfort

Wang Jingqi1, Li Peng2, 3, Peng Zhiyong4, WangXue5, Li Zhaomeng5

(1. CRRC Dalian Co., Ltd., Dalian 116021, China; 2. Zhuzhou CRRC TIMES ELECTRIC Co., Ltd., Zhuzhou 412001, China; 3. Southwest Jiaotong University, Chengdu 610036, China；4. Guangzhou locomotive maintenance depot, Guangzhou 510000, China; 5. China Railway Shenyang Group Co., Ltd., Shenyang 110000, China)

.

U270.2

A

1003-4862（2023）02-0014-06

2022-08-08

王景琪（1984-），男，高级工程师。研究方向：机车电气系统。E-mail: wangjingqi.dl@crrcgc.cc