A Method for Reducing Ocean Wave-Induced Magnetic Noises in Shallow-Water MT Data Using a Complex Adaptive Filter

WU Yunju, LUO Ming, 2), *, LI Yuguo, 2), GE Jiaqi, and PAN Lindong

A Method for Reducing Ocean Wave-Induced Magnetic Noises in Shallow-Water MT Data Using a Complex Adaptive Filter

WU Yunju1), LUO Ming1), 2), *, LI Yuguo1), 2), GE Jiaqi1), and PAN Lindong1)

1),,,,266100,2),,266237,

In shallow-water areas, the marine magnetotelluric (MT) method faces a challenge in the investigation of seabed conducti- vity structures due to electrical and magnetic noises induced by ocean waves, which seriously contaminate MT data. Ocean waves canaffect electric and magnetic fields to different extents. In general, their influence on magnetic fields is considerably greater than that onelectric fields. In this paper, a complex adaptive filter is adopted to reduce wave-induced magnetic noises in the frequency domain. The processing results of synthetic and measured MT data indicate that the proposed method can effectively reduce wave-induced magnetic noises and provide reliable apparent resistivity and phase data.

shallow-water areas; wave-induced magnetic noises; complex adaptive filter; MT data processing

1 Introduction

In recent years, the marine magnetotelluric (MT) methodhas been widely used to investigate geoelectrical structuresbeneath the seabed in mid-ocean ridges (Baba., 2006),subduction zones (Worzewski., 2010), and coastal areas(Ueda, 2014). In a marine MT survey, ocean bottom electromagnetic receivers are deployed on the seabed to col-lect natural electromagnetic signals, which can be process- ed to study the electrical structure beneath the seabed.

When conductive seawater moves by ocean currents andsurface gravity waves through the Earth’s geomagnetic field,electric and magnetic fields are induced (Longuet-Higgins., 1954; Weaver, 1965). These induced fields will seriously interfere with natural MT signals, especially in shal- low-water areas, where wave-induced electromagnetic fieldsare more intense and complex (Ueda., 2014). The ob- served ocean MT data show that wave-induced electro-magnetic fields have a strong energy, and they are the main noises in MT data (Bhatt, 2011); as a result, the quality of MT data is greatly reduced, rendering this information use- less. Ocean waves can affect electric and magnetic fields but to different extents. In general, wave-induced magneticnoises have a notably larger influence on MT data than in-duced electric noises; thus, suppressing wave-induced mag-netic noises is important (Lezaeta., 2005; Neska,2013).

Unlike narrow-band noises, such as power-frequency noise, wave-induced magnetic noises have broad bands at frequencies between 0.01 and 1Hz (Ueda., 2014), and they persist throughout MT data acquisition. In this frequency range, the amplitude spectrum of the magnetic field shows strong energy and a peak. Traditional MT processingmethods, such as least square, robust estimation, and remote reference methods, assume that the deviations caused by noises follow a Gaussian distribution (Guo., 2017), and the deviations can be effectively eliminated usingstatistical methods. The deviations caused by wave-inducedmagnetic noises, however, do not satisfy the Gaussian distribution. Hence, the abovementioned methods cannot effectively re- duce wave-induced magnetic noises.

In the frequency range of wave-induced magnetic noises,a reasonable processing result cannot be obtained (Duan., 2020). Wave-induced magnetic noises should be sup- pressed before estimating the impedance tensor. However, the separation of wave-induced magnetic noises from MT signals in the time and frequency domains is difficult. For the frequencies at which wave-induced magnetic noises occur, we expect to remove the noises and keep the effective signals intact. However, with the use of traditional me- thods, such as Fourier transform, wavelet transform, and singular value decomposition, effective signals can be easily damaged, and it often fails. Several methods for reducing seawater motion induced electromagnetic noises have been proposed in recent years. Lezaeta. (2005) and Neska. (2013) employed the tilt recordings of MT receivers to suppress seawater motion induced magnetic noises. Chen. (2020) used the current meter data collected during MT data acquisition to reduce seawater motion induced electromagnetic noises. These methods required the synchronous collection and recording of other information whenacquiring MT data. They cannot be applied when this kind of information is not collected or is missing.

The recently developed adaptive filter is an optimal filtering method, and it does not require a priori statistical regularity of a signal or noise. Adaptive filters have been successfully applied in the fields of communication, speech signal processing, image processing, and pattern recognition (Widrow., 1986; Zheng, 2010;Han, 2018). Adaptive filtering methods have also been applied to geophysical data processing. Buttkus and Bönnemann (1999) proposed an adaptive time-slice filter method to improve the signal-to-noise ratio of deep seismic reflections in pre-stack data. Jeng. (2009) reduced the random noise in ultra- shallow seismic and ground-penetrating radar data by two- dimensional (2D) adaptive filters. Li (2017) adopted an adap-tive filtering method to process marine controlled-source electromagnetic data. Hattingh (1989) proposed a correlated data-adaptive noise cancelling method for the remo- val of biased, random, man-made, and impulsive noises from land MT data. In this paper, a complex adaptive filter is extended to marine MT data processing to eliminate wave- induced magnetic noises in the frequency domain. The me- thod requires no additional synchronous information and can only be applied to reduce wave-induced magnetic noises of marine MT data.

In the following, we first briefly describe the complex adaptive filtering algorithm. Then, the method is applied to process the simulated and measured MT data. Finally, we draw conclusions from this paper.

2 Complex Adaptive Filtering by Least Mean Square (LMS) Algorithm

The key to adaptive filters is to find an appropriate sig-nal that is coherent with the effective signal or noise in con- taminated data. Then, the noise can be reduced using the adaptive filtering method. Ocean waves have a considera- bly larger effect on magnetic fields than electric fields, anda linear relationship exists between these fields in the fre- quency domain. Hence, the spectra of magnetic fields at the frequencies of wave-induced magnetic noises can be re-constructed using a complex adaptive filtering method. Thereconstructed magnetic spectra will be less affected by wave-induced magnetic noises.

The complex adaptive LMS algorithm is widely used for complex signal and information processing (Zheng, 2010; Han, 2018). The algorithm can automatically adjust the filter coefficients based on the statistical characteristics of input and output signals and minimize the mean square error between output and reference signals. In step, the output signal() can be expressed as the product of the adaptive filter coefficient() and the input signal():

where the superscriptindicates the conjugate transpose of a matrix. The residual error() is defined as the diffe- rence between the reference() and output signals():

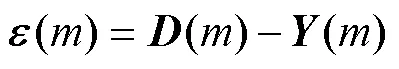
In step+1, the adaptive filter coefficient is given by the following (Han, 2018):

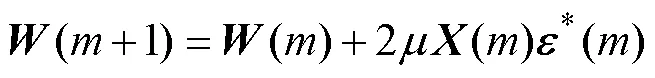
where the superscript * indicates the complex conjugate of a matrix,is the adaption step size, which satisfies 0<<1/max, withmaxbeing the maximum eigenvalue of the correlation matrix=[()X()].

In the marine MT method, naturally occurring electromagnetic fields are used to study the electrical structure be- neath the seafloor. In the frequency domain, the horizontal components of electric and magnetic fields (and) at the seafloor are assumed to be linearly related and can be expressed as follows:

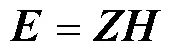
where=(E,E)Tand=(H,H)Tare the horizontal components of electric and magnetic fields, respectively, andindicates the impedance tensor written in matrix form

In the following, we will deal only with wave-induced magnetic noises. The magnetic fields can be defined as the sum of signals and noises:

where subscriptsandrepresent the signals and noises, respectively. Notably, the magnetic signalsatisfies Eq. (4), but the magnetic noise () does not. Meanwhile, the noises in the electric fields are ignored (=0).

Eq. (4) can be reformulated as follows:

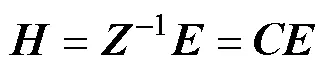
where=−1is the inverse of the impedance tensor. Hence,combined with MT data, the complex adaptive filtering LMS algorithm can be expressed as follows:

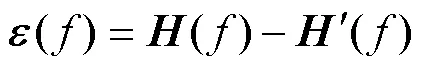
whereis the frequency, andis the predicted magnetic field. In Eqs. (7)–(9),,, andare the output, reference, and signal, respectively.

The iteration process repeats, and the predicted magnetic fieldis obtained by multiplying the electric fieldby the tensor, which is adjusted by calculating the differencesbetween the predicted () and measured () magnetic fields. With the iteration, when the predicted magnetic fieldapproaches the measured magnetic field, the differ- renceis close to the wave-induced magnetic noises. And the process is shown in Fig.1.

Fig.1 Flow chart of wave-induced magnetic noise suppression based on the complex adaptive filter.

The processing steps of the complex adaptive filter are summarized as follows:

1) The time series of marine MT data are transformed into the frequency domain using the Fourier transform to obtain the horizontal electric fieldand magnetic field.

2)(1) is set to zero. The iteration starts at the lowest frequency without the wave-induced magnetic noise and ends at the highest frequency. The tensoris converged to the optimal solution using Eqs. (7)–(9).

3) The measured magnetic field() at the frequencies without the wave-induced magnetic noises remains unchanged, and the measured magnetic field() at the frequencies with the wave-induced magnetic noises is replaced by the predicted magnetic field(). In this manner, we reconstruct the magnetic fields, which are less affected by wave-induced magnetic noises.

4) The reconstructed magnetic fields are transformed intothe time domain by the inverse Fourier transform to obtain the denoised time series of magnetic fields. Then, the ori- ginal time series of magnetic fields are replaced by the de- noised time series, and the wave-induced magnetic noises are reduced.

3 Synthetical MT Data Processing

To illustrate the effectiveness of the method in reducing magnetic noises generated by ocean waves proposed in this paper, we use a 1D geoelectric model (Fig.2) to simulate MT data (Ernst., 2001; Loddo., 2009). When si- mulating MT data, we need to obtain the horizontal magnetic field () and the impedance tensor () in the frequency domain andthe horizontal electric field () using Eq. (4). Then, we transformandinto the time domain using the inverse Fourier transform to obtain the time se- ries of MT data.

We first simulate the MT response over the model shown in Fig.2 and obtain the impedance tensor (). Second, we determine the magnetic response () by transforming the time series of magnetic fields of MT data collected at a site in the South China Sea, in which the water depth is 700m and assuming that the wave-induced magnetic noisesare almost completely attenuated, into the frequency domainusing the Fourier transform. Then, the horizontal electric responsecan be obtained with Eq. (4). Finally, with the use of the inverse Fourier transform, we acquire the time series of the simulated MT data at a sampling rate of 5Hz and 50000 data points (Fig.3).

Fig.2 1D three-layer ocean geoelectric model.

3.1 Electric Fields Without Noise

The horizontal components of MT data at frequencies between 0.09 and 0.4Hz and collected in the South Yellow Sea, in which the water depth is approximately 20m, are seriously disturbed by wave-induced magnetic noises, and the energy of noises is stronger than that of MT signals. We regard the magnetic data in the frequency range of 0.09–0.4Hz as wave-induced magnetic noises and extract them using a band-pass filter. Then, we add them to the simulatedmagnetic fields to create the synthetic MT data. Fig.4 shows the simulated magnetic fields of the MT data (namely, the pure signal), wave-induced magnetic noises, and contaminated data (synthetic data). To show the details more clearly, we display only the first 100 data points of the time series and only the frequencies between 0.09–0.4Hz of the amplitude spectra. The amplitude spectra of the contaminated data present an evidently strong energy in the frequency band influenced by wave-induced magnetic noises. We use the complex adaptive filtering method to process the synthetical data.

To evaluate the performance of the complex adaptive filtering method, we calculate the signal-to-noise ratio (SNR), normalized root-mean-square error (NRMSE), which re- presents the difference between the denoised data and pure signal, and correlation coefficient (CC) of the data before and after filtering (Wang., 2017), which are defined as follows:

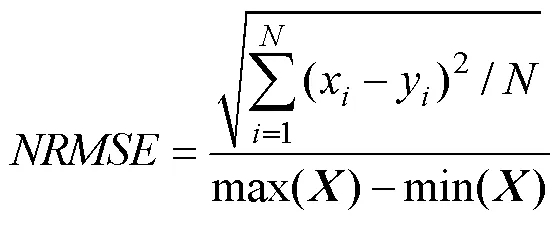
Fig.5 shows the time series and amplitude spectra of the pure signals, denoised data, and errors (differences between pure signals and denoised data). The denoised data are close to the pure signal. Table 1 shows the,, andbefore and after filtering the synthetic MT data. After the application of the complex adaptive filtering me- thod, theof horizontal magnetic fields (HandH) in the frequency band affected by wave-induced magnetic noises increase from −19.9621dB to 37.3028dB and from −4.7704dB to 25.9763dB, respectively. Thebe- tweenHand pure signal decreases from 4.9754% to 0.0617%, and that betweenHand pure signal decreases from 3.0812% to 0.1774%. ThebetweenHand pure signal increases from 0.8647 to 0.9999, and that betweenHand pure signal increases from 0.9132 to 0.9997. Thus, after the application of the complex adaptive filtering me- thod, the wave-induced magnetic noises are almost completely removed.

Fig.3 Time series of simulated MT data. From top to bottom: Ex, Ey, Hx, and Hy.

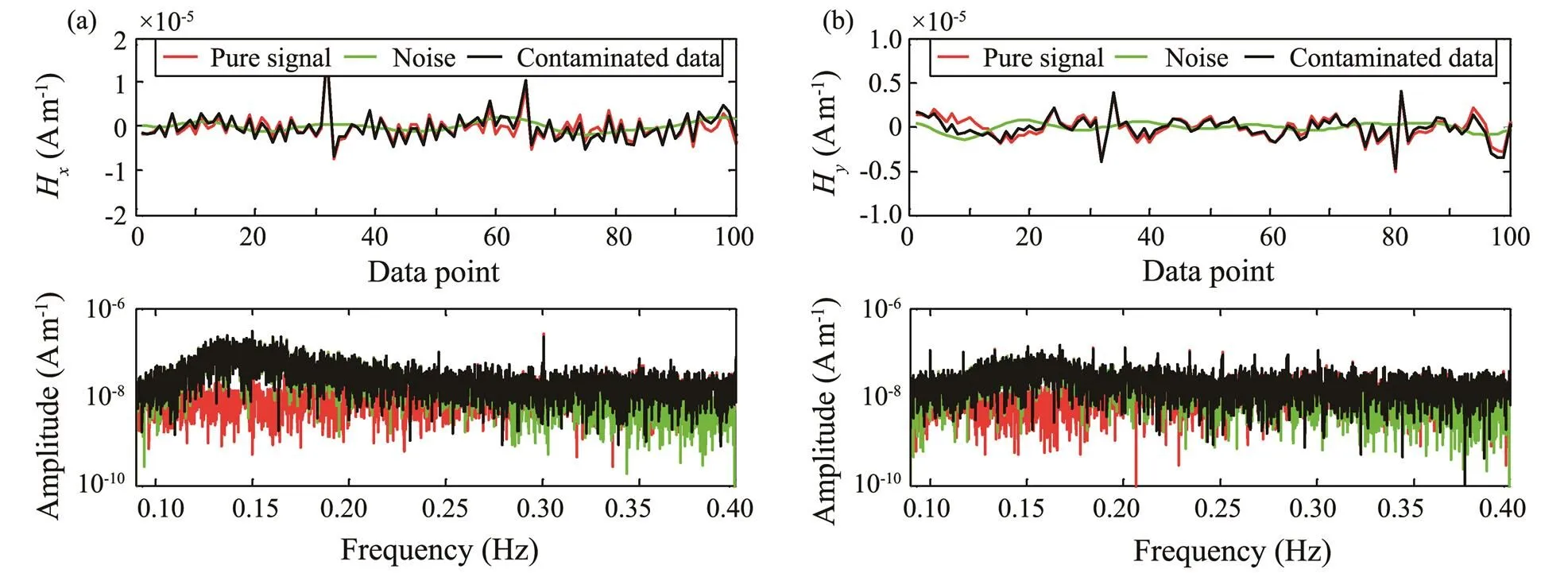
Fig.4 Time series (top panel) and amplitude spectra (bottom panel) of the pure signal, noise, and contaminated data. (a), Hx; (b), Hy.

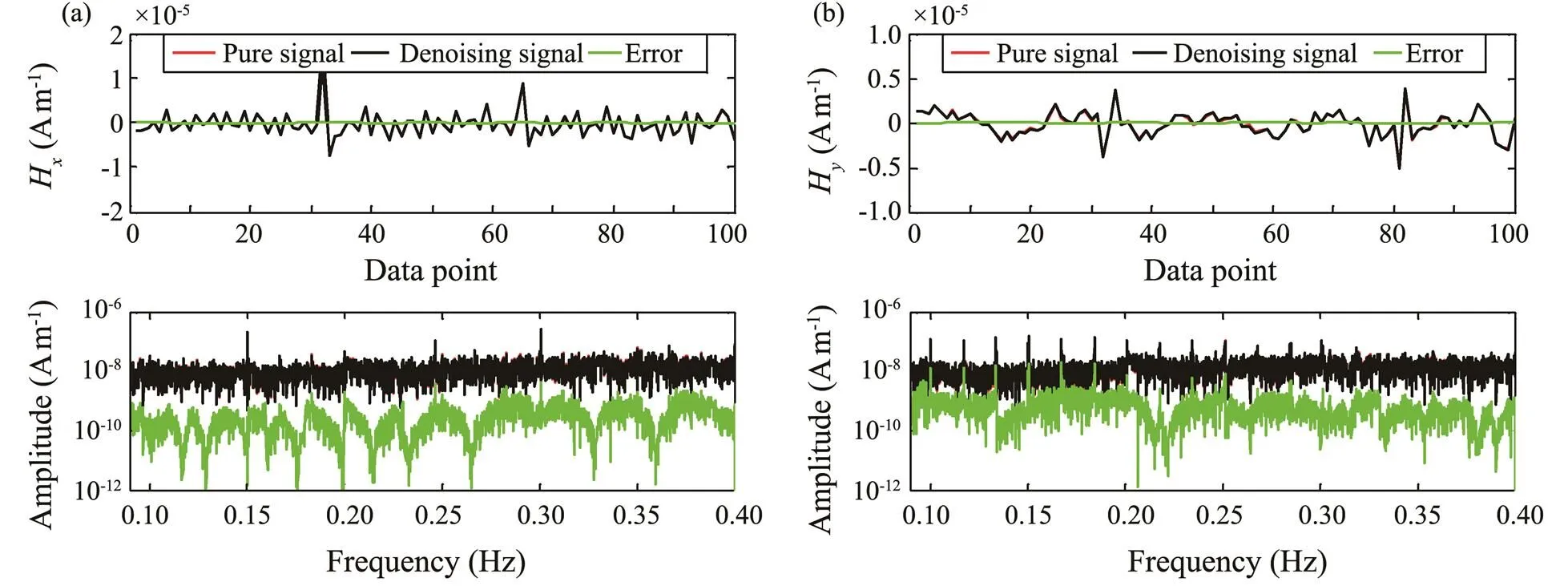
Fig.5 Time series (top panel) and amplitude spectra (bottom panel) of pure signals, denoised data, and errors. (a), Hx; (b), Hy.

Table 1 Three evaluation parameters before and after filtering

The robust M estimation method is adopted to estimate the MT impedance tensor (Egbert and Booker, 1986; Chave., 1987; Larsen, 1989; Smirnov, 2003). For the MT datawith noise, the estimated impedance tensor will deviatefrom the real one. The reference channel must be as noise-free as possible to eliminate deviations (Hattingh, 1989). The magnetic fields of ocean MT data are more susceptible to noises than electric fields. The robust M-estimator is given by the following:

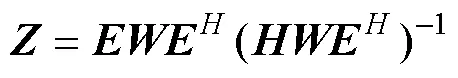
whereis the weight matrix with diagonal elements:

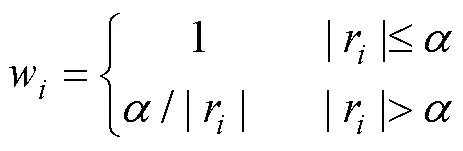
whereris the normalized residual, andis set to 1.5.

The impedance tensorcan be obtained by the robust M-estimator shown in Eq. (13). Meanwhile, the apparent resistivity and phase can be further attained. Fig.6 shows the apparent resistivity and phase of the synthetic MT data before and after filtering. For the processing results of the synthetic MT data in the period from 2.5s to11s (0.09–0.4Hz), that is, when wave-induced magnetic noises occur, the estimates of apparent resistivities and phases deviate from the true values remarkably. After the application of the complex adaptive filtering method, the deviations are significantly reduced, and the estimated values of apparent resistivities and phases are close to the true values. The processing results of the synthetical MT data reveal that the complex adaptive filtering method can effectively reduce wave-induced magnetic noises and provide reliable apparent resistivities and phases.

3.2 Electric Fields with Random Noise Added

Ocean waves interfere with the electric and magnetic fields but to different extents. The interference of waves in ele- ctric fields is substantially less than that in magnetic fields. The extraction of wave-induced electric noises from the col- lected ocean MT datasets is difficult. As an alternative, the wave-induced magnetic noises extracted from measured MT data in the frequency range between 0.09 and 0.4Hz are added to the simulated magnetic fields, but 10% random noises are added to the simulated electric fields. Fig.7 shows the time series and amplitude spectra of the puresignals, de- noised data, and errors. Table 1 also displays the parameters used to evaluate the effectiveness of the proposed method. Fig.7 shows that after the application of the complex adaptive filtering method, the denoised data are close to the pure signals, and the wave-induced magnetic noises are almost completely removed.

Fig.8 shows the apparent resistivity and phase of the synthetic MT data before and after filtering. After the app- lication of the complex adaptive filtering method, the deviations are significantly reduced, and the estimated appa- rent resistivities and phases are close to the true values. Theprocessing results of electric fields with 10% random noises are similar to those without noise. As shown in Figs.6 and 8, some noises exist in the electric fields, but the processing results are barely affected.

4 Measured MT Data Processing

We conduct an MT survey in the South Yellow Sea, Chi- na (Duan, 2020). The collected information shows that the MT data are contaminated by the wave-induced magnetic noises at frequencies between 0.09 and 0.4Hz.Especially at frequencies between 0.1 and 0.2Hz, the noisesare very strong, the estimated apparent resistivity and phase curves are distorted, and the error bars are very large.

The complex adaptive filtering method is applied to theprocessing of the measured MT data. Fig.9 shows the am- plitude spectra of the magnetic fields before and after the application of the complex adaptive filtering method on a seafloor MT site where the water depth is approximately 20m. The magnetic fields (HandH) are significantly af- fected by ocean waves, and bumps (strong energy) at fre- quencies between 0.09 and 0.4Hz are observed. The bumpsdisappear after the application of the complex adaptive fi- ltering method.

Fig.6 Apparent resistivities (top panel) and phases (bottom panel) of the synthetical data. Red triangles and black dots indicate the processing results with and without the use of the complex adaptive filtering method, respectively. (a), ρxy and φxy; (b), ρyxand φyx.

Fig.7 Time series (top panel) and amplitude spectra (bottom panel) of the pure signals, denoised data, and errors. (a), Hx; (b), Hy.

Fig.8 Apparent resistivities (top panel) and phases (bottom panel) of the synthetical data. Red triangles and black dots indicate the processing results with and without the use of the complex adaptive filtering method, respectively. (a), ρxyand φxy; (b), ρyx and φyx.

Fig.9 Amplitude spectra of H-fields before and after adaptive filtering. The black line indicates the amplitude spectra of the contaminated data, and the red line denotes the amplitude spectra of the denoised data. (a), Hx; (b), Hy; (c) and (d), Hx and Hy between 0.09 and 0.4Hz.

Fig.10 shows the apparent resistivities and phases of the MT data before and after the application of the complexadaptive method. For the processing of results of the original MT data, at periods between 2.5 and 11s, when wave- induced magnetic noises occur, we fail to obtain stable apparent resistivities and phases. After the application of the complex adaptive method, the apparent resistivities andphases notably improve. The processing results of the mea-sured MT data show that the complex adaptive filtering me- thod can effectively reduce wave-induced magnetic noises and obtain reliable apparent resistivities and phases.

5 Discussion and Conclusions

In shallow-water areas, marine MT data are seriously contaminated by wave-induced electromagnetic noises. In general, wave-induced magnetic noises have a considerablylarger influence on the MT data than electric noises. To improve the data processing results, scientists should aim at the reduction of wave-induced magnetic noises. The spec- tra of magnetic fields at the frequencies of the wave-induced magnetic noises show a strong energy and a peak. The deviations caused by wave-induced magnetic noises do not follow Gaussian distribution, and the traditional MT processing methods cannot obtain reliable results.

In this paper, we assume that electric fields are noise- free and propose a complex adaptive filtering method to reduce wave-induced magnetic noises in marine MT data. The spectra of magnetic fields with wave-induced magne- tic noises can be reconstructed using the proposed method. The proposed method is used to process synthetic MT responses over a 1D electrical conductivity model and mea- sured MT data collected in a shallow-water environment. The data processing results show that the proposed methodcan effectively suppress wave-induced magnetic noises and obtain a reliable estimate of apparent resistivity and phase curves.

Fig.10 Apparent resistivities and phases of the measured data. Red triangles indicate the processing results of raw data, and the black dots indicate the processing results after the complex adaptive filtering method. (a), ρxy and φxy; (b), ρyx and φyx.

Our work notably has some limitations. The electric fieldsof the marine MT data contain wave-induced electric noises, although they are notably smaller than magnetic noises. However, in this paper, we opt not to reduce these noises. We should attempt to reduce these noises in the future. In the proposed method, we adjust the step size until satisfactory filtering results are obtained. Future work should focus on the optimization of the algorithm. In addition, the method can only be successfully applied if fewer noises are present in the electric or magnetic fields.

For the synthetic MT data, the pure signal and noise are known, and one can evaluate the filtered results quantitatively using the SNR, NRMSE, and CC. However, for the measured MT data, as the pure signal and noise are unknown, the filtered results can only be qualitatively evaluated by viewing the characteristics of the apparent resistivity and phase curves obtained after the application of the proposed method. We should attempt to find a suitable criterion to quantitatively evaluate the filtered results of the measured MT data in the future.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Nos. 91958210 and 41904075). Thanks are due to the Laboratory of Marine EM Detection Technology and Instrument R&D (OUCEM) for providing the MT data.

Baba, K., Chave, A. D., Evans, R. L., Hirth, G., and Mackie, R. L., 2006. Mantle dynamics beneath the East Pacific Rise at 17˚S: Insights from the Mantle Electromagnetic and Tomography (MELT) experiment., 111 (B0201): 1-18.

Bhatt, K. M., 2011. Motion induce noise in marine electromagnetic data. PhD thesis. Technische Universität Braunschweig.

Buttkus, B., and Bönnemann, C., 1999. Enhancement of deep seis- mic reflections in pre-stack data by adaptive filtering., 156 (1-2): 253-278.

Chave, A. D., Thomson, D. J., and Ander, M. E., 1987. On the robust estimation of power spectra, coherences, and transfer functions., 92 (B1): 633-648.

Chen, K., Zhao, Q., Deng, M., Luo, X., and Jing, J., 2020. Seawater motion induced electromagnetic noise reduction in marine magnetotelluric data using current meters., 72 (4): 1-11.

Duan, S., Li, Y., Pei, J., Zhao, T., Wu, Z., Han, B.,., 2020. Carbonate imaging with magnetotellurics in a shallow-water environment, South Yellow Sea, China., 178: 1-9.

Egbert, G. D., and Booker, J. R., 1986. Robust estimation of geo- magnetic transfer functions.,87 (1): 173-194.

Ernst, T., Sokolova, E. Y., Varentsov, I. M., and Golubev, N. G., 2001. Comparison of two techniques for magnetotelluric data processing using synthetic data sets.,49 (2): 214-243.

Guo, J., Guo, R., and Liu, J., 2017. The progress of research in magnetotelluric impedance estimation method., 14 (4): 409-414 (in Chinese with English abstract).

Han, F. M., 2018.. 2nd edition. China Machine Press, Beijing, 103-104.

Hattingh, M., 1989. The use of data-adaptive filtering for noise removal on magnetotelluric data., 53 (3-4): 239-254.

Jeng, Y., Li, Y., Chen, C., and Chien, H., 2009. Adaptive filtering of random noise in near-surface seismic and ground-penetrating radar data., 68 (1): 36-46.

Larsen, J. C., 1989. Transfer functions: Smooth robust estimates by least-squares and remote reference methods., 99 (3): 645-663.

Lezaeta, P., Chave, A. D., and Evans, R. L., 2005. Correction of shallow-water electromagnetic data for noise induced by instrument motion., 70 (5): G127-G133.

Li, Z. L., 2017. Study on marine controlled-source electromagnetic data de-noising based on adaptive filtering method. PhD thesis. China University of Geosciences.

Loddo, M., Schiavone, D., and Siniscalchi, A., 2009. Generation of synthetic wide-band electromagnetic time series., 45 (2): 289-301.

Longuet-Higgins, M. S., Stern, M. E., and Stommel, H., 1954. The electric field induced by ocean currents and waves with applications to the method of towed electrodes.,13 (1): 1-37.

Neska, A., Nowozynski, K., Reda, J., and Jegen-Kulcsar, M., 2013. Reducing motion noise in marine magnetotelluric mea- surements by means of tilt records., 194 (1): 304-315.

Smirnov, M. Y., 2003. Magnetotelluric data processing with a robust statistical procedure having a high breakdown point., 152 (1): 1-7.

Ueda, T., Mitsuhata, Y., Uchida, T., Marui, A., and Ohsawa, K., 2014. A new marine magnetotelluric measurement system in a shallow-water environment for hydrogeological study., 100: 23-31.

Wang, H., John, C., Cheng, J., Zhu, G., Wei, W., Jin, S.,., 2017. Synthesis of natural electric and magnetic time-series us- ing inter-station transfer functions and time-series from a neigh- boring site (STIN): Applications for processing MT data., 122 (8): 5835-5851.

Weaver, J. T., 1965. Magnetic variations associated with ocean waves and swell., 70 (8): 1921- 1929.

Widrow, B., Stearns, S. D., and Burgess, J. C., 1986. Adaptive signal processing edited by Bernard Widrow and Samuel D. Stearns., 80 (3): 991-992.

Worzewski, T., Jegen, M., Kopp, H., Brasse, H., and Castillo, W. T., 2010. Magnetotelluric image of the fluid cycle in the Costa Rican subduction zone., 4: 108-111.

Zheng, B. Y., 2010..4th edition. Publish- ing House of Electronics Industry, Beijing, 183-218 (in Chinese).

(September 27, 2021; revised December 10, 2021; accepted January 12, 2022)

© Ocean University of China, Science Press and Springer-Verlag GmbH Germany 2023

Corresponding author. E-mail: luoming@ouc.edu.cn

(Edited by Chen Wenwen)