贝叶斯网络变量消元法最优消元顺序构造

任东平 郭建喜 郝小礼 蒋涛

1.海军勤务学院基础部；2.海军装备部装备保障大队

变量消元法（Variable Elimination， VE）是贝叶斯网络众多推理算法中最基本的一个，其推理的快慢和复杂度主要取决于消元的顺序。寻找最优消元顺序是一个非确定性多项式难解算法（Nondeterminism Polynomial Hard， NP-Hard）问题，在实际中常采用启发式搜索来求解。为了提高变量消元法的推理速度，在此对最小度、最大势、最小缺边和最小增加复杂度搜索方法进行了研究，以亚洲网络为例，分析计算了上述搜索方法的复杂度和消元顺序，通过MATLAB R2018a对上述不同搜索方法分别进行网络构建和推理，最后通过推理时间分析比较了4种搜索方法的性能。实验结果表明最小增加复杂度搜索方法优于其他搜索方法，其平均耗时最少为0.012s，可加快贝叶斯网络的推理过程。

贝叶斯网络源于Pearl[1]提出的不确定知识表示模型，因其有着概率论的严谨理论基础，以图模型清晰地表示随机事件之间的相互依赖关系，成为人工智能、模式识别和故障诊断等领域的研究热点[2]。贝叶斯网络推理主要有两种方法：精确推理和近似推理。精确推理主要有变量消元法（Variable Elimination）、团树传播算法（Clique Tree Propagation）、多树传播（Polytree Propagation）和图约简算法（Graph Reduction）等。其中，变量消元法是最基本的推理算法，也较容易理解，其优势在于它的通用性和简易性，能够很好地解决复杂贝叶斯网络的推理，尤其是复杂的故障诊断贝叶斯网。

变量消元法的复杂性主要取决于其消元的先后顺序，寻找最优消元顺序是一个NP-难解问题[3]，目前普遍采用近似算法求解，主要有最小度搜索[4]、最大势搜索[2，5]、最小缺边搜索[2]，向光军通过对变量消元法的分析，提出了最小缺边搜索（Minimum Deficiency Search， MDS）和变量消元并行运行的算法[6]，但该算法没有找到最优的消元顺序，仍存在一定的缺陷；高文宇提出了一种新的搜索算法——最小增加复杂度搜索[7]，但只是通过仿真实验进行说明，而没有用到实例中，未给出其搜索方法的具体实现过程，也没有和上述搜索方法进行对比。针对以上问题，本文以贝叶斯网络经典模型亚洲网络来验证上述搜索算法在变量消元法中的优劣。

1 贝叶斯网络

贝叶斯网络（Bayesian Network）是一个有向无环图，其中的节点表示事件中的随机变量，有向边则表示节点之间的相互依赖关系。每个节点都有概率分布，根节点的概率分布属于边缘分布，也可称为先验概率；非根节点则是条件概率。

在概率论中，可以用条件概率链[8]的形式表示其联合概率，其形式如式（1）所示：

公式（1）也可以称为链规则，其中Y为随机变量，P（Y1,Y2,… ,Yk）是Y1,Y2,… ,Yk的联合 概率，P（Yi|Yi-1, … ,Y1）是Yi,Yi-1, … ,Y1的条件概率。

将贝叶斯网络条件独立性假设用于链规则公式（1）可得到如式（2）所示：

其中P（Yi|Parent（Yi））为贝叶斯网络节点Yi的条件概率，Parent（Yi）表示Yi的直连父节点。

为了下文论述，在这里引入贝叶斯网络的一个经典模型——亚洲网络[9]。抽烟可能会引起肺癌或者支气管炎，出访亚洲可能会导致肺结核，这3种疾病的任何一种都有可能会导致呼吸困难。若有肺结核或者肺癌，X光胸透结果可能呈阳性，把这些因果关系结合起来，便得出了经典的亚洲网络模型，如图1所示，其中V表示到过亚洲，T表示感染肺结核，S表示抽烟，L表示患有肺癌，B表示患有支气管炎，E表示感染肺结核或者患有肺癌，X表示拍摄X光，D表示呼吸困难。用公式（2）表达如图1所示中的各个节点的联合概率分布可得到如式（3）所示：

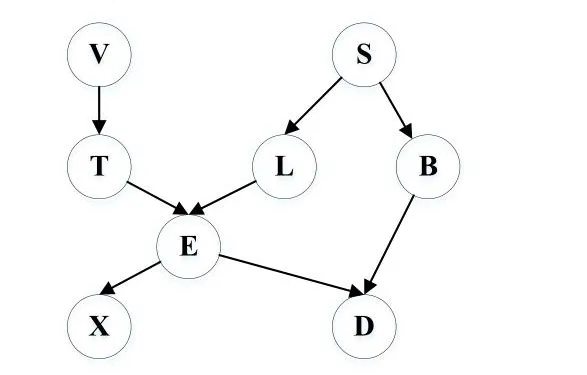
图1 亚洲网络模型Fig.1 Asian network model

如表1所示为亚洲网络节点概率，其中P（i）表示节点i的先验概率，P（i|j）表示在j为真时节点i的条件概率，）表示在j为假时节点i的条件概率。

表1 亚洲网络节点概率Tab.1 Probability of asian network nodes

2 变量消元法

假设F是关于变量集X={X1，X2，…，Xn}的一个函数，而f={f1，f2，…，fm}也是一组函数，其中f所涉及的变量都是变量集X的一个子集。如果则f为F的一个分解，f1，f2，…，fm称为F的分解因子。消元方式可以分为两种。一种是从F={X1，X2，…，Xn}出发，通过的方式完成X1的消元；另一种从f={f1，f2，…，fm}出发，将与X1的所有相关函数{f1，f2，…，fk}，利用公式行消元，并将返回到f中，就实现了X1的消元。

通过以上叙述，若采用第一种消元方式，其计算的复杂度相对于变量的个数n成指数增长；若采用第二种消元方法，其计算的复杂度仅仅依赖于涉及X1的分解因子f1,f2,… ,fk的变量数量，其计算复杂度会大大减小。

假设用X来表示一个贝叶斯网络N中所有变量节点的集合，用f表示N中所有节点概率分布的集合，依据贝叶斯网络的定义，则f可视为N表示的联合概率分布P(X)的一个分解。假设观测到了证据集E={E1,E2, …,Em}，它们的取值记为e。在集合f的因子中，将所有表示证据的变量设置为实际观测值，就可以得到另一组函数，记之为f ′。这一步骤称为设置证据，f ′是函数P(Y，E=e)的一个分解，这里Y=X∩。

设Y的一个子集为Q，f ′从中依次消去所有在Y中，但不在Q中的变量，就可以得到另一个函数集合，记为f ′′。f ′′是P(Q，E=e)的一个分解，将f ′′中的所有因子相乘便得到P(Q，E=e)。按照条件概率的定义可得到如式(4)所示：

VE算法需要提供5个输入量：（1）贝叶斯网络N，同时也是联合分布P（X）的一个分解；（2）证据变量的集合E；（3）证据变量集合E的取值e；（4）查询变量的集合Q；（5）所有不在Q∪E中的变量的排序ρ，即为消元的顺序。对于联合分布P（X）的获取采用公式（2），只需按照网络拓扑图写出联合分布即可；证据集变量集合E以及E的取值e均由人员观测得到；查询变量Q即为所求事件；消元顺序ρ的获取需要通过搜索方法来获取，不同的搜索方法获取不同的消元顺序，以上即为变量消元法的输入量。VE推理算法的代码实现如表2所示。

表2 VE算法的实现过程Tab.2 Implementation process of VE algorithm

3 消元复杂度分析

从变量消元法的实现过程可以看出，最耗费时间和内存的步骤是对Elim(f，Z)这一函数的调用。这一函数的运算量远超其他步骤的运算，所以说整个变量消元法的计算复杂度主要是由这一函数来决定的。

函数Elim(f，Z)表示从f中挑出所有包含Z的函数{f1，…，fk}，将它们相乘，得到中间函数G，再从G中消去Z。设X1，…，Xk是G中所有除Z之外的变量，如果把函数表示成多维表，则G所需存储的函数个数为综上所述，是函数G复杂性的一个度量，从而也是Elim(f，Z)复杂性的一个度量，称之为变量Z的消元成本，记为δ(Z)[2，6]，如式（5）所示。

用变量消元法进行推理时，需要消去多个变量，设它们依次为Z1, Z2, …,Zn。在这里用总消元成本来衡量变量消元法的总复杂度。以亚洲网络为例，函数集合为f={P（V） ,P（S）,P（T|V） ,P（L|S）,P（B|S）,P（D|B,E）,P（X|E）,P（E|T,L）}。设证据节点为X=1，E=1，计算V的可信度，即求P(V|X=1，E=1)的概率，消元顺序为ρ=＜D,B,L,S,T＞，网络中所有变量均取二值。消去D时，需要计算G=P(D|B，E)，共涉及3个变量：D、B、E，所以D的消元成本δ(D)=2×2×2=8。依次类推，其余4个节点B，L，S，T的消元成本分别为 4，8，2，4。则按此消元顺序进行消元的总成本为26。

所谓结构图就是考虑一个函数的集合F={f1，…，fm}，F的结构图可定义为从一个空图出发，对F中的每一个变量，在图中相应的添加一个节点，对于任意两个变量X和Y，如果它们同时出现在同一个因子fi中，则在它们对应的节点之间添加一条边。按此规则构建的图模型为结构图。如图2所示为亚洲网络结构图。

图2 亚洲网络结构图Fig.2 Asia network structure diagra m

从一组函数f中消去一个变量Z的成本，能从该函数的结构图中算得。如前所述，从f中消去Z的成本其中X1，…，Xl是除Z之外的变量，Z是函数所涉及到的所有变量，f1，…，fk是所有涉及Z的因子。根据上文对结构图的定义，在f的结构图中，{X1，…，Xl}刚好是所有与Z相邻节点的集合，记为nb(Z)，因此有如式（6）所示：

在亚洲网络中，从f中消去变量T需要计算G=P(T|V)P(E|T，L)，涉及到4个节点{T，V，E，L}，所以在结构图中，与T相邻的节点使nb（T） ={V,L,E}，所以δ(T)也可以按公式（5）计算，即

4 消元顺序构造

4.1 最小度法

在结构图中，最小度搜索法就是把度数最小的节点变量放到消元顺序队列的末尾，并在网络中删去该节点和连接该节点的有向边。若有多个节点的度数相同，则任选其一，重复上述过程，直到消去结构图中所有的节点。此消元法称为最小度方法。以亚洲网络模型为例，设证据节点为X=1，E=1，其中1表示事件为真。分别求V，T，S，L，B，D的后验概率。即求P(V|X=1，E=1)，P(T|X=1，E=1)，P(S|X=1，E=1)，P(L|X=1，E=1)，P(B|X=1，E=1)，P(D|X=1，E=1)的概率。采用最小度搜索方法求消元顺序，总消元顺序为ρ=＜E,D,B,L,S,T,X,V＞。求节点V时的消元顺序为ρ=＜D,B,L,S,T＞，由第二节中的公式（3）可得其联合分布为如式（7）所示：

消去元素D如式（8）所示：

消去元素B如式（9）所示：

消去元素L如式（10）所示：

消去元素S如式（11）所示：

消去元素T如式（12）所示：

计算V的后验概率分布得到如式（13）所示：

计算V的最大假设检验得到如式（14）所示：

上述过程即为变量消元法的推理计算过程，在MATLAB R2018a中构建亚洲网络，求得P （V= 1 |X= 1 ,E= 1 ） =0.01，

耗时0.0750s（后续不同搜索方法的推理计算过程均如上，不再赘述）。同样求T时的消元顺序为ρ=＜ D,B,L,S,V ＞；求S时的消元顺序为ρ=＜ D,B,L,T,V ＞；求L时的消元顺序为ρ=＜ D,B,S,T,V ＞；求B时的消元顺序为ρ=＜ D,L,S,T,V ＞ ；求 D 时的消元顺序为ρ=＜ B,L,S,T,V ＞。可得各个节点的推理时间分别为0.0239s，0.0127s，0.0164s，0.0146s，0.0264s。其平均推理耗时为0.0282s。

4.2 最大势搜索

最大势搜索是根据以下规则在无向图中对所有节点进行编号：在有n个节点的无向图中，在第i步中，选择拥有最多已编号的相邻节点，且这些节点未编号，将其编号为n-i+1。如果存在多个这样的节点，则任选其一。当无向图中所有节点都被编完号后，将编号按照由小到大的顺序排序，其顺序就是对应节点的消元顺序，此为最大势搜索方法的一般思想。运用最大势搜索方法求亚洲网络消元顺序：第1步先对B节点编号为8，第2步可对节点S或者D编号，这里将D节点编号为7，第3步对节点S编号为6，第4步对节点L编号为5，第5步对E节点编号为4，第6步可对节点T或者X编号，这里选择将T编号为3，第7步将节点V编号为2，第8步将最后一个节点X编号为1。至此所有节点均已编号，其消元顺序为ρ=＜ X，V，T，E，L，S，D，B ＞。除去证据节点X和E，可的相应节点的消元顺序，求V时的消元顺序为ρ=＜ T，L，S，D，B ＞；求T时的消元顺序为ρ=＜ V，L，S，D，B ＞；求S时的消元顺序为ρ=＜ V，T，L，D，B ＞；求L时的消元顺序为ρ=＜ V，T，S，D，B ＞；求B时的消元顺序为ρ=＜ V，T，L，S，D ＞；求 D 时的消元顺序为ρ=＜ V，T，L，S，B ＞。可得各个节点的推理时间分别为0.0258s，0.0126s，0.0118s，0.0126s，0.0118s，0.0146s。其平均推理耗时为0.0149s。

4.3 最小缺边搜索

无向图中某个节点Z的缺边数就是在用函数Elim(f，Z)消去Z时需要添加的边数。最小缺边搜索一边计算节点的缺边数，一边将节点从无向图中删除。每一步都需计算节点的缺边数，在消去节点时选择缺边数最小的节点进行删除，当同时有多个节点的缺边数相同时，任选其一，如此循环，直到所有节点均被删除。仍以亚洲网络模型为例，在初始时，节点{V，S，T，L，B，E，X，D}的缺边数分别为 {0，1，2，2，2，8，0，0}，任选其一，这里选择 V。消去 V后节点{S，T，L，B，E，X，D}的缺边数分别为 {1，0，2，2，8，0，0}，任选其一，这里选择X。消去X后节点{S，T，L，B，E，D}的缺边数分别为{1，0，2，2，6，0}，任选其一，这里选择T。消去T后节点{S，L，B，E，D}的缺边数分别为{1，1，3，3，0}，消去D。消去D后节点{S，L，B，E}的缺边数分别为{1，1，1，1}，由于节点S，L，B，E构成一个环，所以缺边数相同，可消去任意一个，这里选择消去E，其余3个节点可任意消去，这里选择的顺序为L，S，B。综上所述，最小缺边搜索法的消元顺序为ρ=＜V，X，T，D，E，L，S，B ＞。除去证据节点X和E，可得其他节点的消元顺序，求V时的消元顺序为ρ=＜ T，D，L，S，B ＞；求T时的消元顺序为ρ=＜ V，D，L，S，B ＞；求 S 时的消元顺序为ρ=＜ V，T，D，L，B ＞；求L时的消元顺序为ρ=＜V，T，D，S，B ＞；求B 时的消元顺序为ρ=＜ V，T，D，L，S ＞；求D时的消元顺序为ρ=＜ V，T，L，S，B ＞。可得各个节点的推理时间分别为 0.0150s，0.0122s，0.0119s，0.0119s，0.0121s，0.0125s。其平均推理耗时为0.0126s。

4.4 最小增加复杂度搜索

其主要思想是在结构图中消元时，删除某个节点，与该节点相连的所有边均会被删除，为了降低图的复杂度，往往是希望删除的越多越好，在这里将删去边的条数用ed表示；当节点删除后，需要将删除后的图构成一个完备图，所以会在某些节点之间添加一些边，使其构成完备图，但添加的边又会增加图的复杂度，所以希望添加的边越少越好，将添加的边数记为ea，用ea/ed可得一个新的衡量指标，即最小增加复杂度，用IC表示。选择消元顺序时，先计算出所有节点的IC值，选择IC值最小的进行消元，若有多个相同值，则任选其一，接着计算余下节点的IC值，如此重复，直到所有节点被消去，可得出消元顺序。最小增加复杂度搜索方法是一个动态的搜索过程，从整个网络图出发，对其不断地循环判断，以寻得最优解，提高推理整体的运行时间，避免了局部消元过快而整体较慢的不足。此算法适用于故障诊断时对多查询变量的消元，能够提高整体的运行时间。以亚洲网络为例，运用最小增加复杂度搜索方法，如表3所示为初始状态节点的IC值。

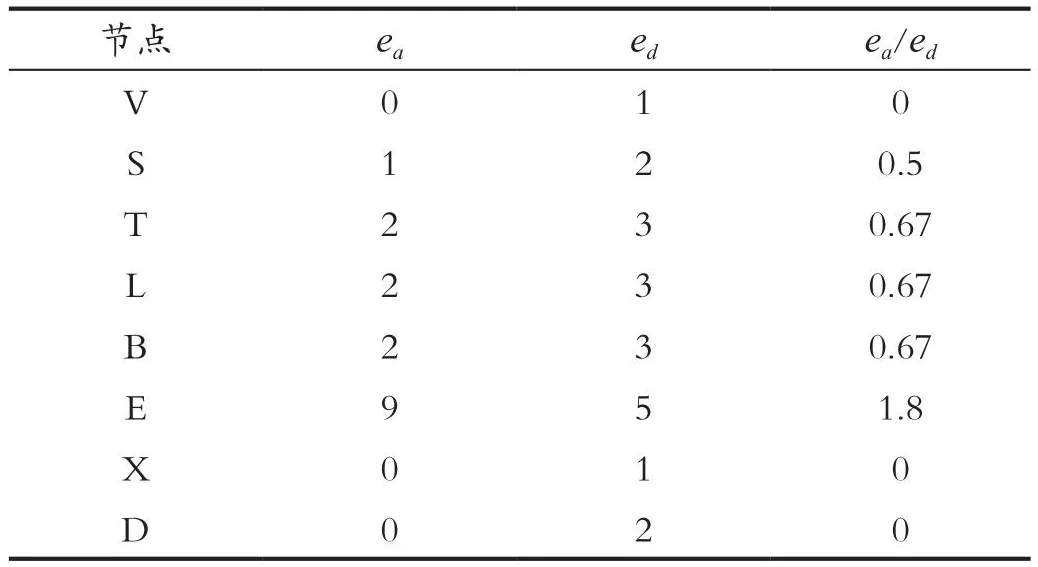
表3 初始状态节点IC值Tab.3 Initial state node IC value

由表3可知，节点V，X，D的IC值均为0，可任选其一进行消元，这里选择节点V，消去节点V后可得其余节点的IC值，如表4所示。

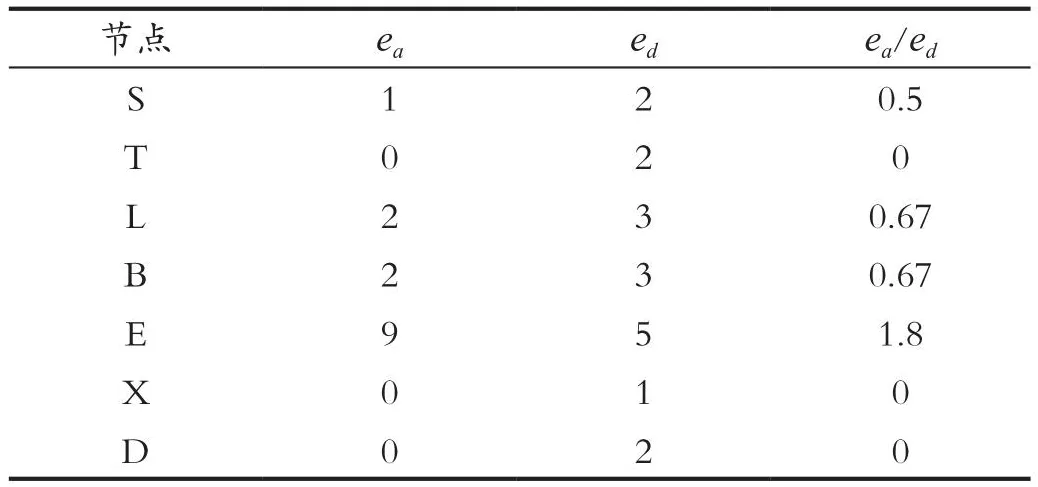
表4 消去节点V后节点IC值Tab.4 Node IC value after eliminating node V

由表4可知，节点T，X，D的IC值均为0，可任选其一进行消元，这里选择节点D，消去节点D后可得其余节点的IC值，如表5所示。

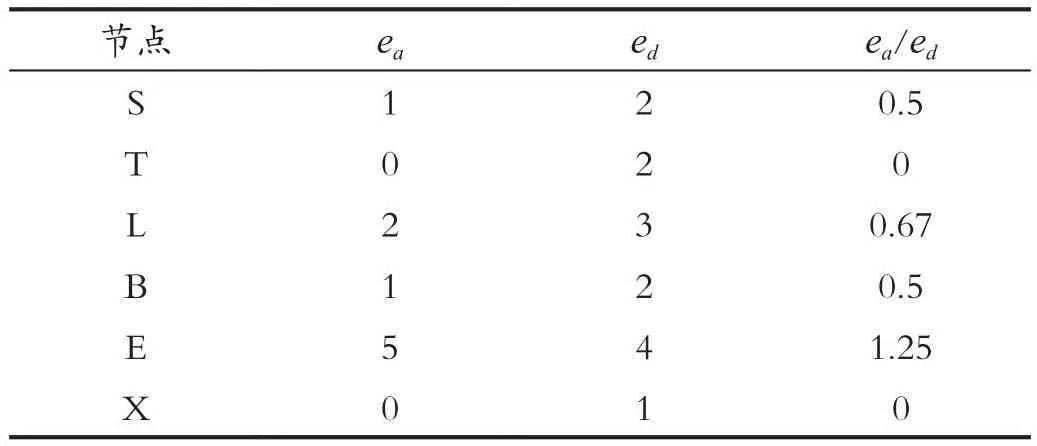
表5 消去节点D后节点IC值Tab.5 Node IC value after eliminating node D

由表5可知，节点T，X的IC值均为0，可任选其一进行消元，这里选择节点X，消去节点X后可得其余节点的IC值，如表6所示。

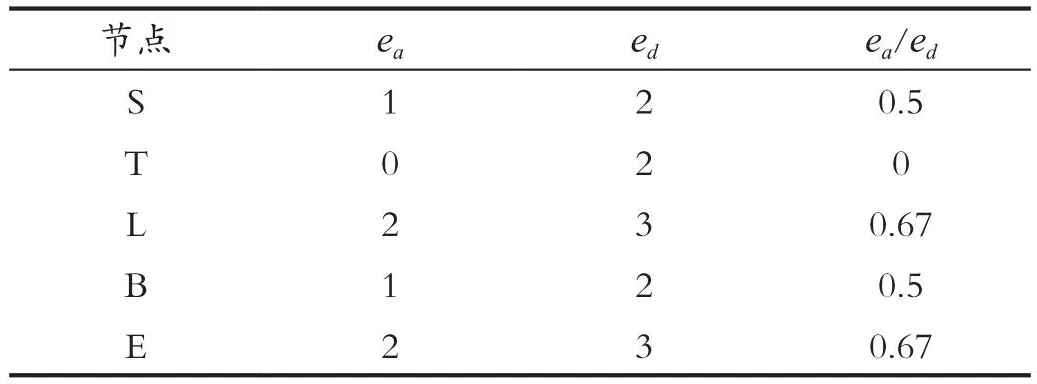
表6 消去节点X后节点IC值Tab.6 Node IC value after eliminating node X

由表6可知，节点T的IC值均为0，消去节点T后可得其余节点的IC值，如表7所示。

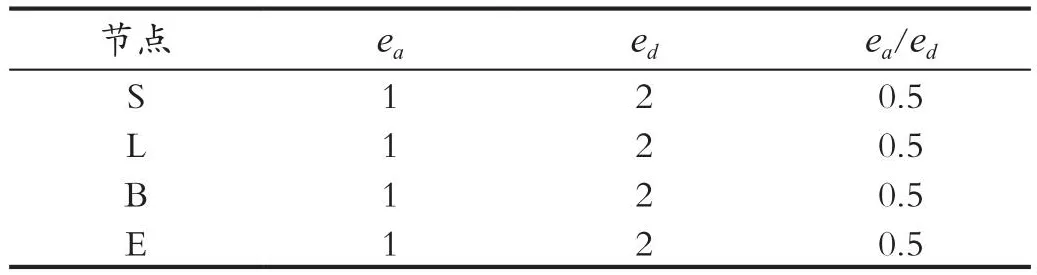
表7 消去节点T后节点IC值Tab.7 Node IC value after eliminating node T

由表7可知，节点S，L，B，E的IC值均为0.5，可任选其一进行消元，这里选择节点S，消去节点S后余下的节点L，B，E构成一个三角图，所有节点都是等效的，可任意组合。最终得出消元顺序ρ=＜ V，D，X，T，X，L，B，E ＞。可得各个节点的推理时间分别为0.0119s，0.0130s，0.0124s，0.0116s，0.0115s，0.0116s。其平均推理耗时为0.012s。如图3所示为4种推理算法平均耗时对比，可以明显的看出最小增加复杂度搜索算法运行时间优于其他3种搜索方法。

图3 不同推理算法对比Fig.3 Comparison of different inference algorithms

5 结语

贝叶斯网络有着广泛的应用前景，可用于人工智能、故障诊断等领域，计算速度的快慢直接决定着该方法在上述领域能否较好的应用。故本文以亚洲网络模型为例，在推理实例中论述了变量消元法的实现过程，通过MATLAB R2018a对亚洲网络进行构造和推理，通过实验分别对比了变量消元法的4种消元顺序构造法，实验表明最小增加复杂度搜索算法优于其他搜索算法，可有效减少推理运算的时间。

引用

[1]PEARL J.Fusion,Propagation,and Structuring in Belief Networks[J].Artificial Intelligence,1986(3):241-288.

[2]张连文.贝叶斯网引论[M].北京:科学出版社,2006.

[3]COOPER G F.The Computational Complexity of Probabilistic Inference Using Bayesian Belief Networks[J].Artificial Intelligence,1990,42(2):393-405.

[4]AMESTOY P R,DAVIS T A,DUFF I S.Algorithm 837:AMD,an Approximate Minimum Degree Ordering Algorithm[J].ACM Transactions on Mathematical Software,2004,30(3):381-388.

[5]BERRY A,BLAIR J R S,HEGGERNES P,et al.Maximum Cardinality Search for Computing Minimal Triangulations of Graphs[J].Algorithmica (New York),2004,39(4):287-298.

[6]向光军,孔兵,欧家钦.贝叶斯网络VE推理算法的并行化研究[J].云南大学学报(自然科学版),2010,32(4):392-395.

[7]高文宇,张力.贝叶斯网最优消元顺序的近似构造算法[J].计算机应用,2011,31(8):2072-2074.

[8]李俭川.贝叶斯网络故障诊断与维修决策方法及应用研究[D].长沙:中国人民解放军国防科学技术大学,2002.

[9]ZHANG N L.Hierarchical Latent Class Models for Cluster Analysis[C]//National Conference on Artificial Intelligence,2002:230-237.

[10][ZHANG N L,POOLE D.Exploiting Causal Independence in Bayesian Network Inference[J].The Journal of Artificial Intelligence Research,1996.