运载火箭姿态控制多速率陀螺融合方法

于海森，王长亮，谭述君，刘玉玺，胡迪科

（1.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116023；2.上海航天技术研究院，上海 201109；3.上海宇航系统工程研究所，上海 201109）

0 引言

大型液体运载火箭的箭体结构是弹性体，随着运载能力和尺寸的增加，越来越呈现出低频密集的特征，加剧了与低频固有振动源（如Pogo 振动、受高空风载所致的箭体振动等）的耦合。这些低频振动信号通过速率陀螺等测量系统进入控制回路，很容易与控制系统相互作用，影响控制系统的稳定性，甚至导致火箭飞行失败。因此，如何有效降低控制回路中弹性信号（尤其是低频部分）的影响是姿态控制系统设计的重要课题。目前，通常采用校正网络或滤波器设计来削弱弹性信号影响，但随着弹性频率降低，这种方式的局限性越来越明显。如何有效地融合多个速率陀螺的姿态测量数据，从源头上减弱进入控制回路的弹性信号，是值得关注的解决方式。

数据融合技术已被广泛应用于很多领域，如邓晨等［1］采用基于梯度信息和高斯过程回归的数据融合方法对飞行器飞行试验辨识数据和风洞试验数据进行融合，其建模结果表明，融合模型预测数据的精度均高于一种数据模型精度。宋欣瑞等［2］提出基于多传感器决策级数据融合的多任务深度学习模型，结果表明，该模型比3 个基线模型的识别准确率平均高出8%；胡胜波等［3］提出火箭飞行数据分布式多尺度融合的研究；司长哲等［4］提出基于Kalman 滤波的数据处理多尺度融合算法；王禹等［5］采用基于Kalman 滤波的多传感数据融合技术使火箭橇信息测量系统获得更好的性能。但目前关于运载火箭多速率陀螺融合技术研究的资料较少。美国国家航空航天局（NASA）在报告中提出了运载火箭的速率陀螺配置方案，根据传感器可安放的位置，依据频率响应数据来优化混杂的传感器的权重系数［6］。该方案被设计用在SLS 发射系统上，证明该方案对火箭的弹性问题有很好作用。NASA 空间飞行中心开发的运载器上升段稳定性分析工具箱ASAT［7］中，角速率的测量用了多个传感器值组合的方法。文献［8］认为运载火箭传感器的布局对控制系统的稳定裕度影响很大，传感器的性能可以通过多个传感器数据组合来改善。文献［9］在火箭控制系统采用速率陀螺冗余方案，一级飞行段采用一级速率陀螺和二级速率陀螺同时进行控制。文献［10］采用多个速率陀螺组合代替单个速率陀螺，提出任意数量速率陀螺组合的斜率计算方法，降低了对全箭模态试验振型斜率选位和斜率测量精度的要求。速率陀螺优化配置和数据融合通往导致复杂的优化问题求解，因此，由于遗传算法及其改进算法全局优化搜索的优势［11］，在实际工程中被广泛应用。RAO 等［12］采用遗传算法研究了平面桁架结构中传感器优化，得到了最优配置；YAO 等［13］将遗传算法应用于航天器传感器优化中，在遗传算子中采用了一种强制变异方法，提升了收敛值，得出了接近最优的方案。李文博等［14］应用基于均匀设计的遗传算法对星载天线上的传感器进行了优化；耿飞等［15］针对卫星太阳能帆板传感器的优化问题，对传统遗传算法的局限性和不足做出改进，提出了自适应改进遗传算法。覃柏英等［16］探讨了单目标和多目标优化的传感器优化配置问题，通过与现有的模态动能法、有效独立法及基于QR 分解的逐步累积法进行比较，传感器优化配置的结果表明，提出的整数编码遗传算法优于上述 3 种方法。实验结果表明，改进的遗传算法对于传感器的配置优化比较有效。

为降低运载火箭姿控回路中弹性信号的影响，基于多个速率陀螺测量的姿态信号，结合姿控回路的传递函数，将多速率陀螺融合问题转化为一个优化问题，通过采用遗传算法进行求解，从而降低弹性对姿态控制的影响，提高控制系统的稳定性。

1 弹性信号对姿控回路的影响

对于大型运载火箭的姿态控制设计而言，箭体的弹性振动不可忽略。弹性振动信号会通过姿态测量装置进入控制回路，从而影响控制系统的稳定性，并且姿态控制系统设计周期长，设计工作复杂困难［17］。

以俯仰通道单通道为例，考虑箭体弹性振动［18］，其俯仰通道的姿态运动学方程为

式中：Δθ、Δα和αw分别为弹道倾角、攻角和风攻角；δφ为俯仰通道的等效摆角；qi为第i阶弹性振动的广义坐标；为横向干扰力bz1为俯仰通道结构干扰力矩；为运动方程系数，具体意义详见文献［19］；Δφ为俯仰角；ξi为第i阶弹性振动阻尼系数；ωi为第i阶弹性振动的固有频率；Qiy为第i阶弹性振动的广义干扰力系数。

考虑到姿态测量装置（如惯组、速率陀螺等）安装在箭体上，因此除测量出刚体姿态运动信息外，还能敏感到弹性振动产生的附加姿态信息，故姿态测量装置所测量的信息为

式中：Δφg为姿态角测量装置测量信息；(Xg)为测量装置安装处的第i阶弹性振型斜率。

经典的火箭控制设计是采用PD 控制律，将测量的箭体姿态通过运算产生发动机摆角指令形成闭环反馈控制，其控制方程为

从上述控制律可以看出，其姿态信息由惯组、速率陀螺等传感器测出，包含了弹性振动的信息，会直接影响到发动机摆角指令，影响姿控系统的稳定性。目前在姿态控制系统设计时，主要通过校正网络的设计实现对弹性信号的抑制，保证系统在各特征秒点和各状态下，刚体、弹性和晃动均有足够的幅值和相角裕度。此外，在做火箭姿态控制时也需要考虑箭体参数和系统参数偏差，考虑偏差最坏组合，构成额定、上偏差、下偏差和弹性上偏差等状态。

降低控制回路中弹性信号影响的另一个思路是利用多个速率陀螺进行测量从源头上降低进入控制回路的弹性信号，不仅会降低火箭控制器设计的难度，还可以增加火箭控制系统的稳定性。事实上，在工程上已有利用速率陀螺的安装位置和两个速率陀螺数据融合等方式抑制弹性信号。例如，采用两套速率陀螺测量装置，分别放在第i次振型波腹的前、后，将这两套速率陀螺测量的信号相加，使第i次振型弹性振动信号抵消，也避免了箭体弹性信息进入系统。而本文则面向两个以上的多速率陀螺测量姿态信息，在经验基础上开展多速率陀螺融合方法研究降低进入控制回路的弹性信息。

2 多速率陀螺融合方法

多速率陀螺融合方法，通过优化多处速率陀螺测量值的权重分配来减少弹性信号对姿态控制的影响。为了降低信号中的弹性信号，定义一个向量λ为速率陀螺的权重分配系数，里面的每一个元素λi代表的是第i个速率陀螺的权重系数，设N为速率陀螺个数，如果λi取0，则表示第i个位置速率陀螺的测量值没有采用，在实际中可以在该位置少配置一个速率陀螺。

建立如下的目标函数：

式中：Hatt(jω)为姿态角的传递函数；Hrat，i(jω)为姿态角角速度的传递函数；a0和a1为控制律系数。

该优化问题的定义是使选定频率范围内摆角指令传递函数中的弹性信号峰值最小，例如弹性信号对应的峰值往往出现在中高频段，可以选择频率ω的范围在0～103rad/s。多速率陀螺融合方法就是通过优化多个速率陀螺的权重分配系数从而使目标函数的值最小，即进入控制回路的弹性信号最弱。因此，需要选择合适的优化算法求解最优的权重分配系数λ。

3 基于遗传算法的求解方法

多速率陀螺融合方法的设计是一个多变量、有约束的非线性规划问题。传统优化算法如罚函数、复合变形法等对于关系复杂、设计变量较多的优化问题，一般收敛速度较慢，且要求目标函数连续可微等，最终结果可能只是局部最优解。随着优化要面对的问题规模和复杂程度的逐渐增大，有学者提出新的优化算法，如遗传算法、粒子群优化法等。由于遗传算法的进化特性，搜索过程中不需要问题的内在性质，对于任意形式的目标函数和约束，无论是线性的还是非线性的，离散的还是连续的，都可处理，而粒子群优化法、神经网络等优化算法主要应用于连续问题。

遗传算法的使用规则类似于概率进化算法，其核心思想引自达尔文的自然进化理论，其主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定，具有内在的隐并行性和更好的全局寻优能力，采用概率化的寻优方法，能自动获取和指导优化的搜索空间，自适应地调整搜索方向，不需要确定的规则。因此，可以基于遗传算法进行优化求解。

将速率陀螺的权重分配系数向量λ作为染色体进行编码、并随机生成一定规模的初始种群；然后根据遗传算子对种群中的个体进行选择、交叉及变异等操作；最终通过迭代逐渐演化出适应度最高的个体，作为权重分配系数的最优解。具体过程如下：

步骤1初始化种群。将多速率陀螺权重分配系数向量λ作为染色体，其中，采用实数编码方式进行编码，并随即生成M个满足约束条件的个体作为初始种群P，进行后续遗传操作。

步骤2适应度函数定义。优化目标是使多速率陀螺测得的姿态信号中弹性信号峰值最小，而遗传算法是保留适应度值大的个体，因此可以将式（4）的中求弹性信号峰值的式子前加入负号作为适应度函数为

步骤3遗传操作。首先对种群个体进行选择，使适应度值较佳的个体保留到下一次迭代；其次对种群中个体进行交叉操作，以保证种群的稳定性，使迭代过程向着最优解方向进行；最后以一定概率进行变异操作，保证种群多样性，避免计算结果陷入局部最优解。

步骤4终止条件判断。对种群个体重复进行遗传操作。若迭代次数达到预设最大值，或达到稳定迭代周期（即最佳个体在一定迭代周期内不发生变化），则结束进化，选择最佳适应度个体作为最终计算结果。

4 算例与结果分析

本算例运载火箭的5 个速率陀螺分别安装在芯级和4 个助推级上，传统上仅采用安装在芯级的速率陀螺信号，作为多速率陀螺融合前的情况，安装在芯级处的速率陀螺作为第一个，即可以用λ=[1 0 0 0 0]来表示；下面算例主要比较采用本文方法对多速率陀螺融合后相对于速率陀螺融合前（即传统上仅采用芯级速率陀螺信号）的效果。

首先通过遗传算法对某个选定秒点的多速率陀螺进行融合，给出该秒点下三通道的多速率陀螺权重系数。分析多速率陀螺融合前后对火箭三通道开环传递函数bode 图的影响，从而分析对控制回路中弹性信号的影响。接着分析在设计好的一套火箭控制器上加入多速率陀螺融合方法后对火箭控制器性能的影响。

4.1 多速率陀螺融合方法对控制回路弹性信号的影响

通过遗传算法得到火箭三通道多速率陀螺融合的结果并对结果进行分析。可以选择运载火箭任意特征秒点或者插值秒点的数据，由于火箭在特征秒点第59 s 处于大风区，因此不妨对第59 s 进行分析。速率陀螺的个数为5，即式（5）中N=5，种群规模设置为100，最大迭代次数设置为100，稳定迭代周期设置为50。针对俯仰通道通过遗传算法得到种群的最佳适应度值和平均适应度值如图1 所示。由图1 可以看出，在迭代100 次后，最后种群的最佳适应度值0.631 5 与最后种群的平均适应度值0.632 3 十分接近，从曲线也能看出，最后适应度值呈收敛趋势。

图1 遗传算法得到的最佳适应度值和平均适应度值曲线Fig.1 Beat fitness and mean fitness curves obtained by the genetic algorithm

第59 s 点俯仰通道、偏航通道和滚动通道的速率陀螺权重分配系数λ的最终结果和最佳适应度值fval的结果，见表1。

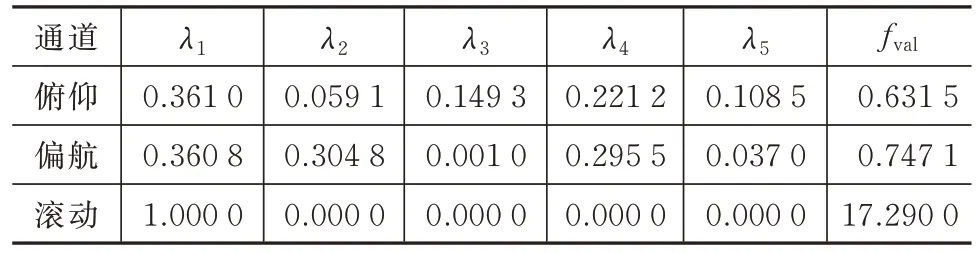
表1 俯仰通道优化结果Tab.1 Optimized results of the pitch channels

由表1 可以看出，滚动通道进行多速率陀螺融合的结果和融合前一样，即只采用第一个速率陀螺已经是最好结果。

在该特征秒点的数据下进行俯仰通道开环传递函数bode 图分析，多速率陀螺融合前后俯仰通道bode 图的对比如图2（a）所示，加入速率陀螺融合以后，弹性第一阶峰值有所下降，融合前峰值为15.60 dB，融合后峰值0.63 dB，下降大约14.97 dB，可以得出加入速率陀螺融合技术后，有降低控制回路弹性信号的作用，并且，融合后峰值的数值0.630 0 与遗传算法的最佳适应度值0.631 5 十分接近，说明采用式（5）作为遗传算法的适应度函数可以准确地找到选定频率范围内的弹性最大信号，再通过遗传算法得到适应度值最小（即弹性最大信号最低）的多速率陀螺权重系数，从而达到采用多速率陀螺融合方法降低弹性信号的作用。俯仰通道和滚动通道的开环传递函数bode 图如图2（b）、图2（c）所示。从图2（b）可以看出，加入多速率陀螺融合后弹性第一阶峰值有所下降，融合前峰值为15.90 dB，融合后峰值为0.74 dB，峰值下降约为15.16 dB，弹性信号有所降低。图2（c）滚动通道多速率陀螺融合前后的bode 图重合，也说明了针对滚动通道只采用第一个速率陀螺已经是最优结果。

图2 三通道多速率陀螺融合前后bode 图对比Fig.2 Bode diagrams of the three-channel multi-rate gyro before and after fusion

因此，采用多速率陀螺融合方法可以有效地降低控制回路中的弹性信号。此外，对于大型运载火箭控制系统，控制系统与弹性模态的关联性需重视，尤其是一阶弹性频率与刚体固有频率比较接近，很可能刚弹产生激振，导致系统失稳［20］。而采用多速率陀螺融合方法后开环传递函数bode 图弹性一阶峰值降低，刚体的截止频率几乎没有发生改变，因此可以十分有效地降低火箭控制器的设计难度，并提高了火箭控制系统的稳定性。

4.2 多速率陀螺融合方法对控制器性能的影响

研究速率陀螺融合方法在控制器设计中的应用效果。在多速率陀螺融合前，时域系统上设计了一组控制器参数，包括3 个通道的控制律系数以及3 个通道的校正网络，仍然分析第59 s 点的控制器性能，采用表1 的三通道速率陀螺权重系数。

火箭的控制器性能体现在开环传递函数bode 图的相角裕度、幅值裕度和弹性一阶稳定情况，工程上一般要求在标称数据下满足相角裕度大于40°，幅值裕度大于6 dB，弹性一阶峰值稳定。通常情况下弹性一阶峰值采取相位稳定的方式，因为弹性一阶的振型斜率测量比较准确，同时考虑到弹性一阶峰频率靠近截止频率，采用幅值稳定的可能会使相交裕度达不到目标要求。

在设计和分析火箭单秒点控制器性能时，不仅需要考虑火箭在标称数据下的情况，也需要考虑偏差情况，使得所设计的控制器在标称数据情况下满足上述要求，在偏差数据情况下保持稳定。本算例同时考虑了火箭标称数据情况、上偏差情况、下偏差情况和弹性上偏差情况。多速率陀螺融合后对控制器性能的影响结果，见表2。

由表2 可以看出，采用多速率陀螺融合技术后，标称和偏差情况下的相角裕度都略微有所下降，但是下降得不多，对控制器性能影响很小，并且可以通过微调控制律系数等方式提高相角裕度。幅值裕度相对多速率陀螺融合前提高了很多，尤其是在上偏差情况，融合前幅值裕度只有4.68 dB，融合后幅值裕度达到了7.32 dB，在有些火箭干扰比较大的秒点下，偏差情况的幅值裕度可能会更低，因此加入多速率陀螺融合技术可以大大提高控制器的稳定裕度。如果在设计控制器前就已经考虑多速率陀螺融合，会降低控制器的设计难度。

表2 多速率陀螺融合在第59 s 点处的控制器性能的影响Tab.2 Effects of multi-rate gyro fusion on the controller performance at the 59th second point

值得说明的是，采用多速率陀螺融合方法后，由于弹性峰值的降低，弹性一阶峰由原先的相位稳定改变为幅值稳定。因此，从总体上考虑，加入多速率陀螺融合技术对控制器性能有所提高，在其他给定秒点或插值秒点具有相似的结果。

5 结束语

本文对运载火箭多速率陀螺融合方法进行研究，建立了多速率融合方法的目标函数，采用遗传算法对多速率陀螺融合方法进行求解。分析多速率陀螺融合前后对火箭三通道开环传递函数bode图的影响，结果表明，采用多速率陀螺融合技术可以有效降低信号中的弹性信号，提高了火箭的稳定性，并有利于火箭控制器的设计。通过在给定秒点设计好的火箭控制器上加入多速率陀螺融合方法，研究对火箭控制器性能的影响，结果表明加入多速率陀螺融合方法可以提高火箭控制器的性能，使火箭更适应偏差情况。