基于强化学习的航天器姿态控制器设计
2023-03-15张瑞卿
张瑞卿,钟 睿,徐 毅
(1.北京航空航天大学 宇航学院,北京 102206;2.上海卫星工程研究所,上海 201109)
0 引言
航天器姿态控制系统是航天器系统中关键的分系统,姿态控制的效果直接影响到航天器有效载荷能否在轨正常工作,如低轨气象卫星需要通过姿态控制系统实现对月定标来完成任务[1]。传统广泛使用的比例-积分-微分(Proportion Integration Differentiation,PID)控制在设计控制器过程中,需要掌握准确的航天器质量参数。但航天器姿态动力学系统十分复杂,模型高度非线性,当航天器的质量参数发生较大改变且无法准备预测时(如捕获非合作对象[2]、燃料长期消耗[3]),PID 控制设计的控制器会出现控制效果不佳,甚至是失效的情况[4]。此外,太空环境还存在很多不确定因素[5],这些都要求设计具备良好鲁棒性和自适应能力的姿态控制器。
传统强化学习方法,如Q-Learning 算法,只能解决小规模、离散空间问题,并没有得到广泛的使用[6]。近年来,深度学习的研究得到快速发展,研究者们也尝试将深度学习和传统强化学习方法结合起来进行研究,进而研究出了很多著名的算法[7],如深度Q 学习算法(Deep Q-Network,DQN)[8]、深度确定性策略梯度算法(Deep Deterministic Policy Gradient,DDPG)[9]。其中,DDPG 算法由于其状态空间和动作空间连续,被广泛应用于连续控制领域[10-13]。
将深度强化学习应用到控制领域时,通常需要根据控制系统的特点设计回报函数[14]。对于航天器的姿态镇定问题,如果认为只在进入精度范围内时获得奖励,那么当训练步数越多时,获得奖励的概率就越小,最终导致训练失败,这被称为稀疏回报问题[15]。吴恩达[16]提出了回报塑造概念,通过人为设计辅助回报函数引导算法收敛,可以减少训练时间,提升训练效果。在连续控制领域中,通常会设计与距离相关的辅助回报函数进行引导[17]。
拟使用DDPG 算法对航天器姿态控制器进行设计。在设计过程中,首先,建立深度强化学习方法训练控制器所需的环境,设定回报函数,搭建基于Actor-Critic 的神经网络框架;然后,使用DDPG算法对姿态控制器进行训练,迭代若干回合完成对姿态控制器的训练。
1 航天器姿态动力学建模
为了描述航天器姿态,规定参考坐标系为轨道坐标系ox0y0z0。在轨道坐标系ox0y0z0中,原点为航天器的质心o,z0轴指向地心,x0轴指向轨道速度方向且与z0轴方向垂直,y0轴与x0轴、z0轴垂直且共同构成右手直角坐标系。采用由轨道坐标系(ox0y0z0) 按z、x、y的顺序旋转到本体坐标系(oxbybzb)的欧拉角来描述航天器姿态,使用ψ、φ、θ分别表示偏航角、俯仰角、滚转角。
航天器姿态动力学方程为
式中:I为航天器转动惯量;ω为姿态角速度;M为作用在航天器上的力矩。
将此方程投影到航天器本体主轴坐标系中:
式中:Ix、Iy、Iz为航天器投影到本体系中的转动惯量;ωx、ωy、ωz为航天器投影到本体系的角速度;Mx、My、Mz为航天器受到的力矩投影到本体系上的分量。
若只考虑航天器姿态镇定控制问题时,航天器姿态的欧拉角都是小量。考虑航天器绕地球旋转的轨道角速度,将姿态运动学方程代入式(2)后,可进一步将姿态动力学方程线化为线性常系数微分方程,即
式中:Ω为轨道角速度;Tcx、Tcy、Tcz为控制力矩;分别为ψ、φ的一阶导数;分别是ψ、φ、θ的二阶导数。
考虑重力梯度力矩,当卫星在小姿态角的情况下,投影到主坐标系下的重力梯度力矩为Tdgx和Tdgy,其表达式为
2 基于DDPG的航天器姿态控制器训练
2.1 DDPG 算法原理
DDPG 算法是一种基于Actor-Critic 框架的算法。基于Actor-Critic 框架的强化学习算法将值函数逼近的方法和策略逼近的方法结合在一起,使用策略逼近的思想来设计Actor,让Actor 进行动作选择,保证了动作的连续性;而使用值函数逼近的思想设计Critic,Critic 告诉Actor 选择的动作是否合适,由于基于值函数逼近的方法可以做到单步更新,因此也提高了学习效率。在Actor 和Critic 交互过程中,Actor 不断迭代,得到每一个状态下选择每一动作的合理概率,Critic 也不断迭代,不断完善每个状态下选择每一个动作的奖惩值。
DDPG 算法在Actor-Critic 框架的基础上,将值函数逼近和策略函数逼近结合的同时,应用了DQN算法记忆库和冻结目标网络的方法,做到了动作空间和状态空间连续,也提高了学习效率。
DDPG 算法在选择动作时,采用确定性策略μ,即输出概率最大的动作,然后也采用了参数噪声N来增加对环境的探索:
式中:a为实际得到的动作;μ(st|θμ)为神经网络参数θμ在状态s下根据确定性策略μ得到的动作。
可将DDPG 算法的目标函数J(θμ)表示为
式中:γ为Agent 短视的程度,也就是回报的衰减程度;ri为第i步的奖励;E(·)为数学期望。
可以证明在采用确定性策略μ的DDPG 算法中,目标函数J(θμ)的梯度与动作值函数Q的期望梯度相等,故Actor 网络的梯度为
式中:∇θ为网络梯度;μθ为网络选择的策略。
而Critic 网络的梯度为
式 中:Qtarget=r+γQ′(s′,π(s′|θμ)|θQ);θQ为Critic 网络的神经网络参数。
根据式(9)、式(10),可以对Actor 网络、Critic网络的网络参数进行更新[9]。
2.2 训练流程
使用DDPG 算法对姿态控制器进行训练时,首先建立航天器姿态动力学环境,并对姿态控制器随机进行初始化;然后姿态控制器根据当前姿态角和姿态角速度输出控制力矩,在控制力矩作用下航天器姿态角和姿态角速度发生改变,设置的回报函数会根据变化后的状态给出回报,算法将当前时刻的状态st姿态控制器输出的控制力矩at、回报rt和下一个时刻的状态st+1生成样本(st,at,rt,st+1),并存放在缓存区R中,之后从缓存区中随机抽取样本,对控制器进行训练,调整神经网络的参数,迭代若干次之后便可完成对姿态控制器的训练。具体训练流程如下。
步骤1随机初始化Critic 网络Q(s,a|θQ)和Actor 网络μ(s|θμ),权重分别为θQ和θμ。
步骤2初始化目标网络的Q′和μ′,权重分别为θQ′=θQ和θμ′=θμ。
步骤3初始化缓存区R。
步骤4设定训练的总回合数M,开始循环,循环步骤如下。
1)为动作探索初始化一个参数噪声Nt;初始化状态s1,并得到姿态角和姿态角速度的观测值;设定每回合的总控制时长T,开始每回合的循环;根据当前策略和探索动作的参数噪声选择动作,也即选择控制力矩at=μ(st|θμ)+Nt。
2)执行控制力矩at,根据航天器姿态动力学模型,航天器的姿态角和姿态角速度发生改变。得到奖励或惩罚rt,并观测新状态st+1。
3)把(st,at,rt,st+1)作为样本传输到R中储存。
4)从R中随机抽取 minibatch 个样本(st,at,rt,st+1)。
5)设yi=ri+γQ′(si+1,μ′(si+1|θμ′)|θQ′)。
6)通过最小化误差来更新Critic 网络:L=
7)使用 SGD 更新 Actor 网络:∇θμ J≈
8)更新目标网络:θQ′←τθQ+(1-τ)θQ′,θμ′←τθμ+(1-τ)θμ′。
在每个步长中,循环上述1~8 步,直到该回合结束。
步骤5 循环结束,得到训练好的姿态控制器。
2.3 回报函数
将回报函数设计为3 部分:
式中:r1为当回合中姿态角和姿态角速度都满足目标精度范围内时的奖励,设置为常数,在训练后期,r1的设置能够使姿态角和姿态角速度更快收敛到目标精度范围内,提高学习效率;r2为当回合中姿态角或姿态角速度不满足目标精度时的惩罚,也即设计的辅助回报函数;r3为当回合中姿态角或姿态角速度严重超出允许范围时的惩罚,设置为常数。r3的设置,一方面可以避免控制时航天器出现翻滚的情况,另一方面也可以避免计算过程中因数值过大导致训练失败。
设辅助回报函数r2为
式中:αi=|ψ|i+|θ|i+|φ|i、ωi=|ωx|i+|ωy|i+|ωz|i、Mi=|Tcx|i+|Tcy|i+|Tcz|i分别为姿态角、角速度和控制力矩的惩罚项;参数i为计算时所取的指数。辅助回报函数在训练前期时,可引导姿态角,角速度和控制力矩通过训练收敛到0;l0、l1、l2为比例系数,用于调整各惩罚项的大小关系,保证每一项都可以起作用。比例系数的设定应满足当达到目标精度时,使回报函数数值大小落在[-1,1]内,此时训练过程中数值比较稳定。
在进行参数调整时,首先,只保留姿态角惩罚项,调整l0的大小,使得训练出来的控制器能够满足姿态角的目标精度;其次,加入角速度惩罚项,调整l1的大小,使得训练出来的控制器能够满足角速度的目标精度;最后,加入力矩惩罚项,调整l2的大小,使得角速度能够不再震荡。
3 仿真实验和结果分析
使用DDPG 算法对姿态控制器进行训练,训练流程参考2.2 节,对仿真中姿态动力学环境搭建和神经网络搭建的参数进行说明。
3.1 航天器姿态动力学环境
针对三轴稳定航天器的姿态镇定控制进行仿真。设航天器本体转动惯量I=diag[220,210,58] kg·m2。航天器绕地球圆轨道运行,轨道角速度Ω=0.001 rad/s。仿真时需考虑重力梯度力矩的影响。
为了能够更加充分地探索状态空间,训练时每回合初始时刻的姿态角和姿态角速度由系统在一定范围内随机生成。设训练时每回合初始时刻,航天器3 个通道的姿态角和姿态角速度的分量在-30°~30°和-10~10 (°)/s 的范围内随机选择。
使用飞轮控制,设控制力矩范围为-5~5 N·m。在选择控制力矩时加入Ornstein-Uhlenbeck 噪声,噪声可以帮助算法更加充分地探索周围的环境,使训练效率和效果都大大提升。
3.2 神经网络和训练超参数
进行训练的最大步数为106,每回合最大时长40 s,采样时间为0.5 s,奖励衰减值γ为0.99。建立Actor 部分的动作现实网络和动作估计网络、Critic部分的状态现实网络和状态估计网络时,所建立的神经网络均为结构相同的BP 神经网络,使用ReLU函数作为神经网络的激活函数,中间的隐藏层神经元个数为256 个,训练控制器使用的辅助回报函数为式(11),选择i=1,其他条件保持不变。
3.3 仿真结果及分析
为了测试使用强化学习方法训练得到的姿态控制器不依赖于航天器的质量参数,使用训练好的姿态控制器对不同质量参数的受扰航天器实施控制。设初始时刻受扰航天器3 个通道的姿态角均为30°,姿态角速度均为10 (°)/s。设置3 组不同质量参数的航天器,分别为训练时使用的航天器转动惯量I,将转动惯量减小50%的I/2 和将转动惯量增加100%的2I。3 组测试中受扰航天器的姿态角、姿态角速度随时间的变化曲线如图1 所示。

图1 不同转动惯量时姿态角和姿态角速度变化曲线Fig.1 Curves of the attitude angle and attitude angle velocity at different values of the inertia moment
由图1(a)可知,尽管质量参数发生较大的改变,姿态角3 条曲线最终都收敛到了0 附近,并且满足精度要求,由于转动惯量发生变化,而力矩限制范围没有变,因此控制时间会随着转动惯量增大而增大。由图1(b)可知,当转动惯量减小50%时,角速度曲线出现了小幅的震荡,其中z轴的震荡幅度最大,但仍然在误差允许范围内,没有出现发散的情况。通过对比图1 中的曲线可以发现,尽管质量参数发生较大改变,经过DDPG 算法训练的姿态控制器仍然能够较好地完成姿态控制任务,控制器对质量参数变化具有良好的鲁棒性。
测试训练好的控制器是否可以应对系统存在测量误差和存在外界干扰力矩的情况。设测量噪声在-1°≤φ、θ、ψ≤1°和-1 (°)/s ≤ωx、ωy、ωz≤1 (°)/s内随机产生,力矩噪声均值为通过策略选择得到的力矩值,噪声方差为2 N·m。仿真结果如图2所示。

图2 有无噪声时姿态角和姿态角速度变化曲线Fig.2 Curves of the attitude angle and attitude angle velocity with and without noise
图2 为同时加入测量噪声和干扰力矩后,受扰航天器的姿态角、姿态角速度和控制力矩随时间的变化曲线图。由图2 可知,当加入测量噪声和干扰力矩之后,控制系统的调节时间变化不大,但稳态误差有所增大,说明强化学习控制器可以做到在一定范围内的测量噪声和干扰力矩的作用下,使受扰控制器恢复姿态镇定。
对不同辅助回报函数进行实验,训练控制器使用的辅助回报函数为式(11),参数i分别选择0.5、1.0、2.0,分别代表选择了凸函数、线性函数、凹函数。使用不同辅助回报函数进行训练,训练得到的满足要求的控制器训练需要的步数和最终控制器的性能均有所不同。对不同辅助函数训练得到的控制器进行测试,并将测试结果进行整理,见表1。
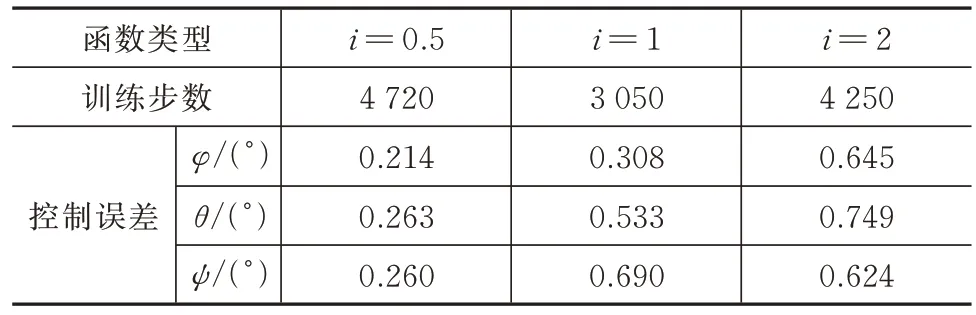
表1 不同辅助回报函数训练效果比较Tab.1 Comparison of the training effects of different auxiliary reward functions
由表1 可知,训练得到控制器的精度随着i的增大而减小,而训练的步数则是当i=1 时最少,但数量级相同。分析其原因,由于设置最终的控制精度绝对值小于1,此时若辅助回报函数取凹函数,则算法训练到后期接近目标控制精度时,辅助回报函数的数量级将会更小,计算出来的更新Critic 梯度也会更小,导致后期辅助回报函数失效,此时无法再向更高的精度收敛,而使用凸函数则可以使精度更高。训练步数方面说明不同i的取值对训练步数的影响不大,需要考虑其他参数设置。
4 结束语
使用强化学习方法对航天器进行了姿态控制器设计。强化学习中,选择了能够用于连续控制领域的DDPG 算法。DDPG 算法能够通过与航天器姿态动力学环境进行互动,得到训练样本,然后随机选择训练样本,根据回报函数计算误差,并对Actor 和Critic 神经网络进行更新,最终通过迭代得到训练好的控制器。强化学习在整个训练过程中没有用到航天器的相关参数,表现出更好的鲁棒性。
通过仿真测试,验证了DDPG 算法设计的控制器对航天器质量参数具有良好的鲁棒性,并且发现了控制器在环境中的力矩干扰和测量噪声也具有一定的控制能力。回报函数设计对强化学习训练效果具有很大影响,因此还对不同回报函数进行对比,实验结果表明,当控制精度绝对值小于1 时,设置凹函数会提高控制器的精度。
但只考虑了强化学习在地面训练控制器后再上天在轨控制,而未考虑强化学习直接在轨进行学习控制,后面将进行在轨学习方面的研究。
