基于RAdam优化的DLSTM-AE交通流预测模型
2023-03-15黄艳国周陈聪左可飞
黄艳国,周陈聪,左可飞
(江西理工大学 电气工程与自动化学院, 江西 赣州 341000)
0 引言
近年来,高速公路的拥堵问题日益严重,随着社会车辆保有量的增加也逐渐暴露出道路基础设施不足的问题,而公路基建的资源瓶颈也影响着交通运输的安全和管理。为了对有限的高速公路资源进行最优的合理调度,道路的交通流预测成为了高速路资源分配十分重要的技术领域,对缓解高速路的拥堵起着至关重要的作用[1-2]。
随着科技的发展,国内外相关学者对公路交通流的预测手段也从传统的基于参数预测转变为当下流行的非参数预测。前者主要以数理统计和微积分等传统数学和物理方法为基础的预测模型,后者则以现代科学技术和方法(如神经网络、深度学习、大数据)为主要研究手段而形成的预测模型[3]。然而,由于参数模型适用的局限性且预测精确度的有限性,在一定程度上难以满足交通流非线性特征的需求[4-5],因此考虑交通流非线性特征的预测模型也随之出现。对非参数模型来说,主要分为浅层机器学习模型和深度学习模型。第1类主要是支持向量回归(Support Vector Regression,SVR)等浅层模型[6-8]。第2类为长短时记忆网络(Long Short-term Memory,LSTM)为代表的循环神经网络模型。其中,由于SVR模型对核的选取比较敏感及大量的参数需求,存在一定的局限性。同时浅层的机器学习模型结构简单,在处理大规模的交通流数据时会遇到结构瓶颈,难以适应大数据的车流量信息。而深度学习凭借着计算机技术发展和海量的车流量数据,逐渐被学者将其应用到预测领域并在试验研究中取得不错的效果。如王祥雪等[9]将LSTM模型用于交通流预测,其试验预测结果显示LSTM模型比传统的RNN模型在其数据集上的评价指标MAE和RMSE分别有所下降。Fu等[10]首次将门控循环单元(GRU)应用于交通流预测,也取得了不错的预测效果。Lü等[11]考虑了交通流空间上的相关性,提出了堆叠式自编码器(Stacked Autoencoder,SAE)模型。虽然上述深度模型的试验预测效果很好,但在实际应用中,模型存在的一些缺陷也随之出现。比如LSTM网络模型本身无法捕捉数据的空间特征,SAE模型没有考虑时序上的影响。研究学者也针对模型的缺陷进行了相应的改进与完善,增加神经网络深度是提高整体性能的有效方法[12]。Sagheer等[13]提出了一种深度长短期记忆网络(Deep LSTM)结构进行时间序列预测,可以更高效地表示长间隔时间序列数据的复杂特征,并采用遗传算法优化参数。由于遗传算法本身存在收敛速度慢及局部搜索能力不足的特点,导致模型训练存在不稳定性。而Liu等[14]提出了一个新的优化算法RAdam,根据方差分散度,动态地打开或关闭自适应学习率,既能保证收敛速度快,也不容易掉入局部最优解。针对交通流时间序列而言,其周期性、空间和时间相关性都对下一步的预测效果产生直接的影响,进一步影响到模型预测的准确度[15-17]。因此,如何综合地提取交通流序列的特征信息是基于深度学习的组合模型亟需解决的关键问题。
为了较为全面地提取交通流特性,本研究根据现有交通流预测方法存在的不足和最优化算法领域的研究成果,提出一种以自动编码器和长短期记忆循环网络为结构基础的交通流预测算法。该算法通过引入深层LSTM模型来获取交通流时间序列潜在的周期性和和时空性特征,利用AE模型作为底层框架,对捕获的特征信息在空间维度上进行解析和重建,进一步增强对交通流数据的时间和空间相关性能力,并结合RAdam算法对组合模型进行全局的优化训练,达到更高预测精确度的目的。
1 DLSTM-AE组合模型的构建
1.1 时间相关性信息提取
LSTM模型是递归神经网络(RNN)的一种特殊网络架构[18],其核心关键在于提出了细胞状态和门机制概念,在一定程度上解决了RNN模型梯度消失问题。但对复杂的时间序列数据而言,深层RNN模型与浅层RNN模型相比,可以更好地表达高维度的非线性和长间隔时间特征,能充分学习到时间序列数据更深层的关联信息。Deep LSTM(DLSTM)是标准LSTM模型的一种堆叠形式,属于深层循环神经网络。每个LSTM块都具有多个LSTM单元,每个单元和下一个LSTM块的对应单元存在前馈连接[10,19]。同时,每个块都在进行不同时间尺度的训练。这种架构在进行反向传播时可以全局调整各个块的参数,对复杂的交通流时序具有较高的非线性拟合能力[20]。
1.2 空间相关性信息提取
自编码器网络是一个简单的3层神经网络,由输入层、隐藏层和输出层依次排列连接,其欠完备自编码器结构如图1所示。AE作为生成模型,每层训练都采用无监督学习算法,其训练过程由Encoder和Decoder 2个阶段组成。交通流数据经过Encoder映射到隐藏层。在该阶段,生成模型会将输入数据进行压缩表示,进行降维,捕获输入的深层特征。再通过Decoder,对原始数据进行重建,生成与输入数据对应的编码格式。

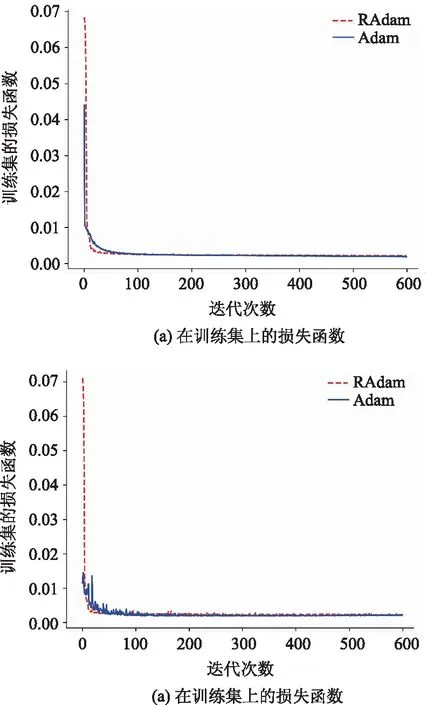
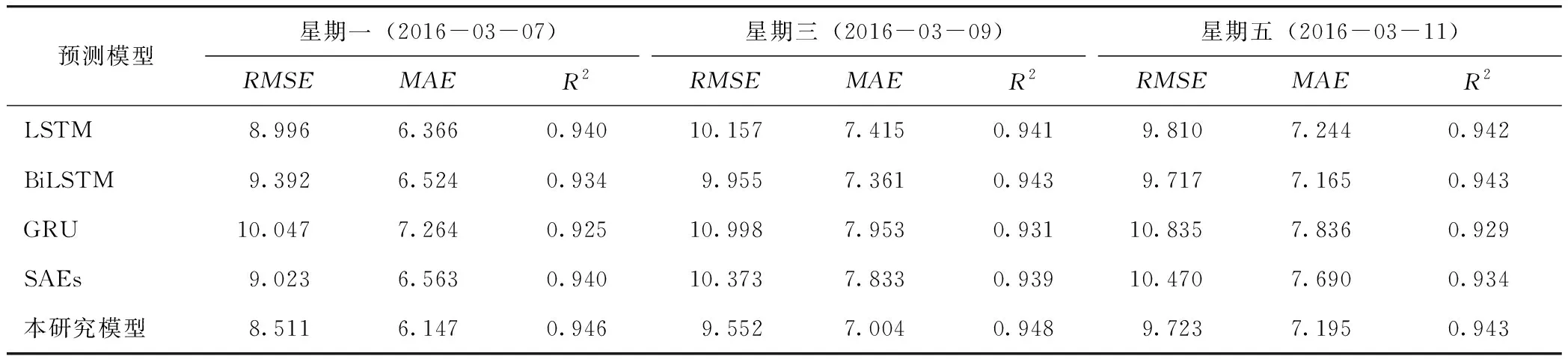
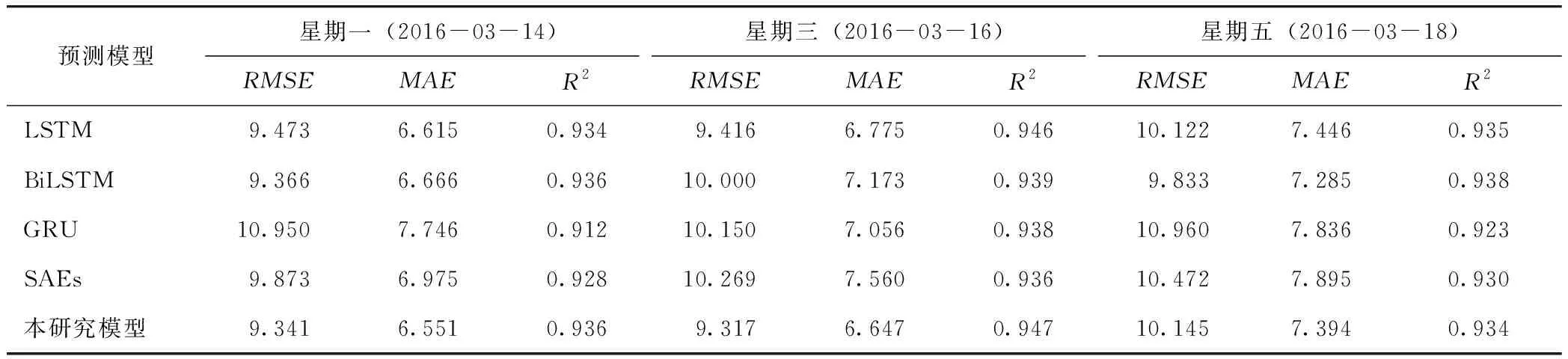
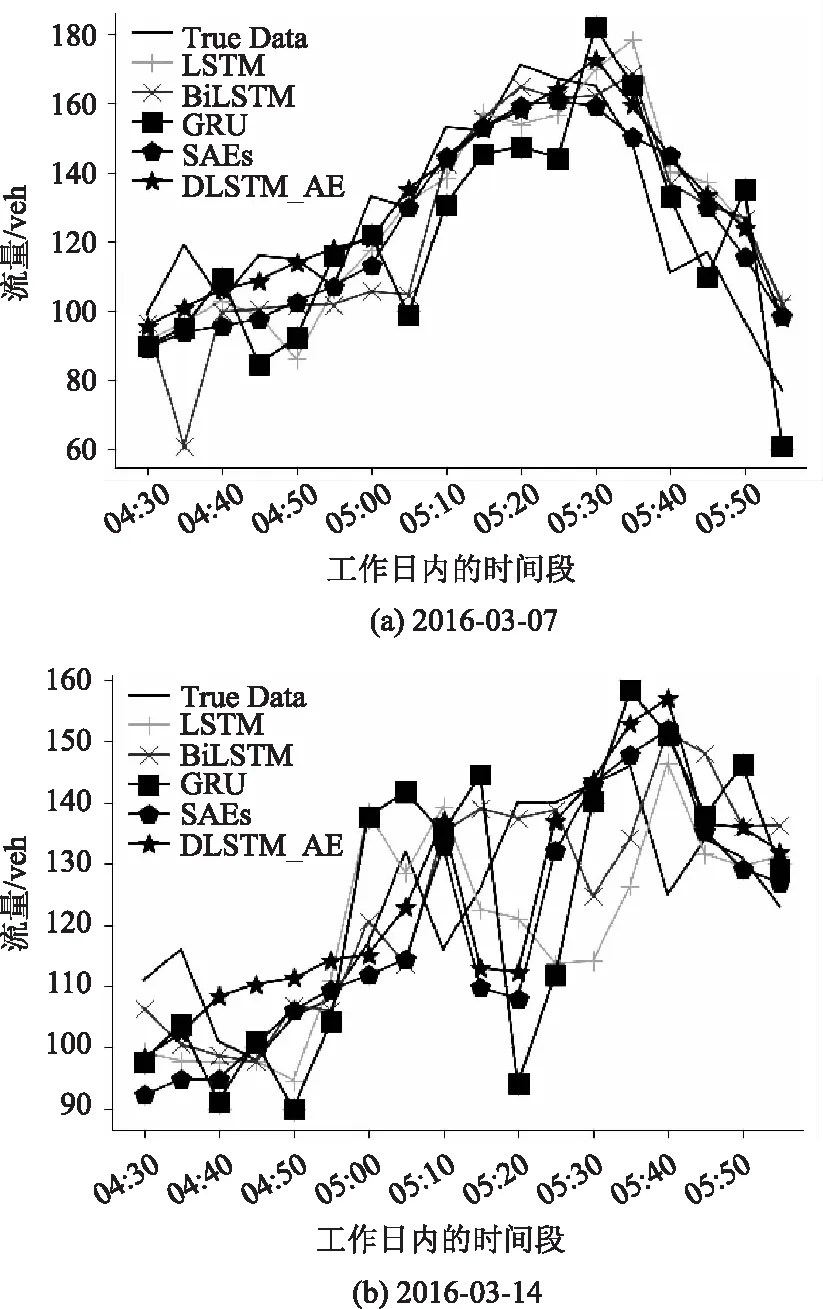
图1 欠完备自编码器结构图(n∈R,j∈R,m 给定1个未标记的交通流输入数据集Xn∈Rm(n=1,2,3,…,N);m,N∈R。AE 2个阶段用公式表示为: H(x)=f(U1x+b1), (1) (2) 本研究提出了一种新架构作为自编码器原始架构的变体,使其能够从时间序列问题中提取特征。特别是,本研究将原始AE架构从前馈神经网络基础更改为DLSTM循环网络基础 (如图2所示),并将其表示为基于DLSTM的自动编码器(DLSTM-AE)。DLSTM-AE依赖于循环神经网络,更适合对时间序列数据进行建模[14]。DLSTM-AE模型的结构如图2所示。 图2 DLSTM-AE模型的架构Fig.2 Architecture of DLSTM-AE model DLSTM-AE模型的预测步骤如下: 步骤1 对原始数据进行归一化,再根据预测目标的间隔时间重新划分成新的训练集和测试集。 步骤2 随机初始化DLSTM-AE模型中的参数W和b,将训练集数据Xt(x1,x2,x3,…,xn),n∈R送入Encoder模块,通过DLSTM模型读取输入数据并将其编码为学习到的表示向量(h1,h2,h3,…,hm,m 步骤6 在训练网络,调整参数阶段,考虑训练期间的变化和动量的影响,选择RAdam优化器对涉及的权重进行迭代更新。 步骤7 训练模型之后,经测试集得出最终的预测序列Y={Yt-(k-1),Yt-(k-2),Yt-(k-3),…,Yt},Yt为模型在t时刻的预测值,Y为模型在t时刻的预测序列。 在以往的模型训练过程中,大多数采用Adam算法进行参数优化。由于Adam优化器在训练初期二阶矩的方差会非常大,而二阶矩指数Vt与优化器的更新梯度方向有关,因此Adam参数更新量的方差也会很大,容易导致在寻找最优解过程中收敛到局部最优。基于Adam改进的Radam优化器的算法优势在于使用warmup的方法进行初期预热,即在训练开始阶段,由随机梯度下降SGD和动量Momentum进行预热,缩小方差。以达到模型更高预测精度的同时提高训练的时效性。RAdam算法步骤描述如表1所示。 表1 RAdam算法步骤Tab.1 Steps of Radam algorithm 当样本批量batch-size大小为256,迭代次数epochs大小为600,滑动窗口lag为12,Encoder-LSTM层数为3,Decoder-LSTM层数为3,LSTM块隐藏神经元个数为32,激活函数为ReLU时,在训练集上的损失函数表现如图3所示。 由图3可知,在损失函数在训练集和验证集的测试中,与Adam优化器比较,RAdam对学习率变化具有良好的时效性和鲁棒性。 图3 RAdam 和Adam分别在训练集和验证集上的损失函数Fig.3 RAdam and Adam in training set and verification set respectively注:图中验证集的损失函数为执行验证集划分validation_split=0.05后的损失值。 本研究试验基于TensorFlow中的Keras神经网络库,在PyCharm开发环境(Windows10专业版,CPU为2.3 GHz,4核,Inter(R) Core(TM) i5-6300HQ,16GB内存)中完成模型的搭建及训练。选取的数据集来自美国加利福尼亚州运输部交通流数据集(Performance Measurement System, PeMS),其数据是从跨越加利福尼亚州所有主要大都市区的高速公路的各个探测器实时收集。通过筛选掉那些节点间距小于5.6 km的检测器,用线性插值法填充缺失值并将输入数据归一化至[0, 1]区间。进行预处理后的数据集包含12 096组数据,其中训练集包含7 777组数据,测试集包含4 321组数据。时间范围从2016年1月4日至2016年3月31日,每组数据的时间间隔为5 min。 在试验过程中,为了科学评估DLSTM-AE组合模型的性能,选用均方根误差RMSE、平均绝对误差MAE和相关系数R2作为模型的评价指标。 (3) (4) (5) 经多次模型训练调试后,最终确定模型参数 batch-size为256,epoch为600次,时间步长为12,激活函数选择ReLU,Encoder解析后的表示向量长度m和Decoder重构后的状态向量长度j均为6,并且将validation-split设置为0.05。 为了验证所提出模型的有效性,选取一些基准神经网络预测模型作为对照组,而本研究提出的模型设置为试验组,通过试验验证进行对比分析。试验数据仍来源于PeMS数据集中,该数据的测试集时间间隔为5 min。其中对照组的试验模型分别为门控循环单元模型(GRU)、长短时记忆网络模型(LSTM)、双向长短时记忆网络模型(BiLSTM)和堆叠式自编码网络模型(SAEs)。就试验预测模型的优化器而言,试验组选择RAdam优化器,对照组选择RMSprop优化器。根据试验组所测试的各项参数结果,对照组与试验组的训练参数保持一致。各试验模型在该数据集上的评估指标如表2所示。 表2 基于PeMS数据集的预测结果Tab.2 Evaluation result based on PeMS dataset 从表中可知,DLSTM-AE模型在PeMS数据集上的平均预测RMSE、MAE值均小于对照组模型,R2值均大于对照组模型,训练时间与GRU模型接近。相比对照组,试验组的RMSE值下降了约0.445~1.826,MAE值下降了约0.282~0.984,R2值提高了约0.005~0.023。而在训练时间上,SAEs模型虽用时最短,其原因在于采用自下而上逐层的非监督预训练,减少了反向传播的时间。但其RMSE和MAE值相比较与试验组分别高出约9.70%与10.43%,R2值降低约1.16%。 试验结果表明,本研究提出的DLSTM-AE组合模型结合了循环记忆网络的预测精确度和自编码器的时效性,在PeMS数据集上的预测表现最优。 为了进一步分析交通流的周期性和时空特性,基于PeMS数据集,分别对2016年3月的2周内多个特定的工作日(星期一、星期三、星期五)进行预测,以更好地评估组合模型的预测性能。DLSTM-AE模型与对照组模型的预测结果如表3和表4所示。 由表3和表4可知,从相邻周的多个特定工作日来看,DLSTM-AE模型随着预测步长增加在评估指标RMSE和MAE值也逐渐上升,R2缓慢下降。表明预测时间的长短对模型性能有较大的影响。但相比较于对照组模型的试验数据,DLSTM-AE组合模型的性能评价指标更具有中心化,模型泛化能力更强。对于试验模型架构来说,DLSTM-AE组合模型对预测时间步长的增加导致模型误差积累的趋势具有减缓效果,弥补了单一模型在长时间预测能力上的不足。 表3 DLSTM-AE模型与对照组模型在第k周下的预测结果Tab.3 Prediction result of DLSTM-AE model and control model in kth week 表4 DLSTM-AE模型与对照组模型在第k+1周下的预测结果Tab.4 Prediction result of DLSTM-AE model and control model in (k+1)th week DLSTM-AE组合模型与对照组模型在特定工作日下早高峰时间段的车流量预测结果如图4所示。 图4 试验模型在多个特定工作日下的预测结果Fig.4 prediction result of experimental model in multiple specific working days 由图4可知,通过对比2幅图的曲线拟合结果,DLSTM-AE模型在实际交通流周期性和时空性的预测数据更加贴合真实数据。当车流量处于高峰时,交通流量处于快速突变状态,会增加交通流预测的难度,但DLSTM-AE模型对比对照组模型可以较好地追踪真实交通流量,较少出现异常的预测值。当车流量处于急剧变化的周期内,会造成模型预测值的精确度下降,而DLSTM-AE模型在此周期结束的下一刻仍准确预测交通流的变化趋势。 本研究将对交通流时序数据的时间维上具有良好拟合效果的DLSTM模型与对空间维上具有优势的AE模型进行组合,充分挖掘了交通流的时空信息。利用RAdam优化算法解决深层循环神经网络的梯度退化问题,从而提高了交通流量预测的准确率。通过仿真试验,对比常用的LSTM,BiLSTM,GRU和SAEs预测模型,对多个特定工作日的交通流进行了预测。本研究提出的组合模型在预测精确度和时效性上均有较好的表现。在相邻周对应工作日的预测结果来看,DLSTM-AE组合模型的预测误差更小,时效性更强,这对城市道路的管理具有重大意义。在后续的工作中,应考虑天气等其他因素的影响,同时模型的实际应用价值也值得进一步研究。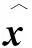
1.3 基于DLSTM-AE组合模型的预测

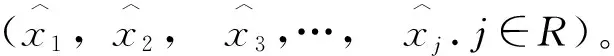
2 基于RAdam的模型优化算法

3 仿真结果与分析
3.1 试验环境与数据来源
3.2 评价指标

3.3 模型参数设置
3.4 基于交通流时空性的预测结果对比分析

3.5 基于交通流周期性的预测结果对比分析
4 结论
