Modeling of magnetized collisional plasma sheath with nonextensive electron distribution and ionization source

Long CHEN (陈龙), Yehui YANG (杨叶慧), Yuhao AN (安宇豪),Ping DUAN (段萍), Shaojuan SUN (孙少娟), Zuojun CUI (崔作君),Zichen KAN (阚子晨) and Weifu GAO (高维富)

School of Science, Dalian Maritime University, Dalian 116026, People’s Republic of China

Abstract The properties of an atmospheric-pressure collisional plasma sheath with nonextensively distributed electrons and hypothetical ionization source terms are studied in this work.The Bohm criterion for the magnetized plasma is extended in the presence of an ion-neutral collisional force and ionization source.The effects of electron nonextensive distribution,ionization frequency,ionneutral collision, magnetic field angle and ion temperature on the Bohm criterion of the plasma sheath are numerically analyzed.The fluid equations are solved numerically in the plasma-wall transition region using a modified Bohm criterion as the boundary condition.The plasma sheath properties such as charged particle density, floating sheath potential and thickness are thoroughly investigated under different kinds of ion source terms, contributions of collisions, and magnetic fields.The results show that the effect of the ion source term on the properties of atmosphericpressure collisional plasma sheath is significant.As the ionization frequency increases, the Mach number of the Bohm criterion decreases and the range of possible values narrows.When the ion source is considered, the space charge density increases, the sheath potential drops more rapidly,and the sheath thickness becomes narrower.In addition,ion-neutral collision,magnetic field angle and ion temperature also significantly affect the sheath potential profile and sheath thickness.

Keywords: plasma sheath, Bohm criterion, nonextensivity, ionization source

1.Introduction

Among the many physical characteristics of plasma discharges,the plasma sheath stands out as a critical component in most plasma experiments and industrial processes,and due to its complicated and variable structure,attempts to construct and simulate physical models of the plasma sheath have attracted widespread interest and research over the past decades [1-10].Generally, when a plasma is adjacent to the container wall or material surface, a region of potential inhomogeneity is an inevitable result, since the ions have a substantially higher mass than the electrons and the electron mobility is at least two orders of magnitude greater than that of the ions, which results in the accumulation of negative charges on the wall and a negative potential in comparison to the bulk plasma.A thin layer of positive space charge, the plasma sheath,is then generated in front of the wall[3].As a non-neutral transition region, the plasma sheath is closely related to various chemical and physical processes.A thorough examination of the sheath properties is essential for understanding the interactions between the plasma and wall in industrial processes such as thin film deposition, surface modification, plasma etching, sputtering, microelectronics,spacecraft propulsion, fusion energy, etc [4-10].

In general, the potential and dynamic properties of the plasma sheath are determined by the sheath boundary conditions.Bohm [11] used fluid models to theoretically derive the condition for a collisionless plasma sheath, called the Bohm sheath criterion.It is stated that the ion velocity at the sheath edge must be at least equal to the sound speed of the ions, which provides the boundary condition for determining the profiles of plasma parameters.Since then, many researchers[5,10,12-28]have tried to investigate the sheath criterion under different physical conditions, such as external magnetic field and ion temperature, and have analyzed the sheath characteristics from different aspects.Nevertheless,most studies have treated the problem without considering the ion source term in the physical model.The source term describes the generation of ions in the system,which gives the number of ions created per unit volume and per unit time[20, 28], and causes a substantially different Bohm criterion and sheath properties compared to the scenario without the source term.For instance, in atmospheric-pressure plasma with low density(such as corona discharge,glow discharge in atmospheric pressure, 1014- 1 016m-3for plasma density)[29-34], the cross section for ionization collision between electrons and atmospheric-pressure neutral atoms is about 10-14m3s-1,and the mean free path is about2.7 × 10-6m[35].Ionization collisions between electrons and neutral atoms are substantial in the sheath region, which provides a large ion source to the sheath formation.The ion-neutral momentum transfer collision cross section is about 5 × 10-15m3s-1[36,37],the ion-neutral collision frequency is aboutνm= 1.4 × 1011s-1,and the corresponding mean free path for ion-neutral collision is about2.4 × 10-8m.For a plasma density around 1014- 1 016m-3,the typical sheath scale is aboutL≈(1 0-2 0)λD≈ 10-2- 10-3m,which is much larger than the above collision lengths.It is of great significance to study the source term effect and influences of collisions on the plasma sheath properties in such plasma conditions.

In recent years, researchers have introduced several possible ion source terms in studies of plasma sheath characteristics.Yasserian et al [27] investigated the structure of the electronegative plasma sheath in the presence of an oblique magnetic field and the constant ion source term.Gyergyek and Kovacic [28] used four different ion source terms in the magnetized plasma sheath model to investigate the magnetized sheath characteristics.For the collisionless magnetized plasma sheath, two different ion source terms were used by Adhikari et al [38] and a comparison of their contributions has been presented.Crespo [39] studied the effects of positive ion temperature and ionization frequency on the plasma sheath considering the ion source term.Moulick et al [40, 41] investigated the structure of a collisional magnetized plasma sheath in the presence of a nonzero ion source with constant ionization frequency.The results of the above researchers suggest that the collision frequency,ionization frequency and magnetic field greatly determine the Bohm criterion.Moreover, the sheath thickness is also affected by the strength and the inclination angle of the magnetic field.

However, in the previously mentioned works, the electron velocity distribution is assumed to satisfy the classical Maxwell-Boltzmann distribution.This kind of assumption is only valid for the macroscopically ergodic equilibrium system, and it is inappropriate for the description of plasma systems with nonthermodynamic equilibrium state[5,42-46].Experimental studies have shown that non-Maxwellian distribution electrons exist in plasma discharge when electron density is around 1014- 1018m-3and electron temperature around 1-5 eV [47-49].Moreover, the ionization collision process may consume and decrease the percentage of highenergy electrons, thus the electron distribution may deviate from the Maxwellian distribution.Thus, Tsallis [50] presented a new statistical method called nonextensive or Tsallis statistics in 1988, extending the concept of entropy to nonextensive generalized entropy, for which the entropySqis stated as follows:

Here, q represents the nonextensive degree of the thermodynamic system,kBis the Boltzmann constant, N is the total number of all microstates,andpirepresents the probability of the ith microstate.Tsallis statistics have been successfully applied to the plasma systems where the particle distribution deviates from the classical Maxwellian distribution.Many works have shown that the Maxwell distribution is inadequate to describe the systems in nonequilibrium states with longrange interactions including plasma, and nonextensive electron distributions were applied to describe them [2, 51-56].The most significant property of the q-entropy is its nonadditivity (i.e.nonextensive feature), which means that the sum entropies of respective independent systems is different from the entropy of the whole system.Therefore, the total entropySq(I,J) of two independent subsystems I and J is represented by the following equation [57, 58]:

As shown in equation (2), whenq=1,the entropy of the composite system is equal to the sum of the entropies of the I and J systems, which means that the q-entropy is reduced to the standard extensive Boltzmann-Gibbs entropy.Whenq＞1,the generalized entropy of the composite system is smaller than the sum of the entropies of the components,which is called sub-extensive; whenq＜1,the generalized entropy of the composite system is greater than the sum of the entropies of the components, which is called super-extensive[59].Experiments on the relationship between high-energy particles and plasma[60]and the observation of space plasma[61] both reported the nonextensive distribution of charged particles, and a subsequent experiment reported that the non-Maxwellian electron velocity distribution was measured in the plasma [47].Comparison between the experimental data and Tsallis’s q-nonextensive formula [62] shows high consistency.However,an experiment on sheath observation with nonextensive electrons has not been reported yet; the reason may be that the sheath is on the scale of several dozens of Debye lengths, and properties such as electron distribution and potential profile of the sheath are hard to measure in experiments.Even so,it can be predicted that it is very likely that electrons cannot reach thermal equilibrium in the sheath region,since the electron density is much lower and electrons are affected by the sheath electric field.

Basnet et al [63] studied electronegative plasma sheath properties with nonextensive distribution of electrons in the presence of a constant ion source, and systematically compared the sheath structures with and without the source term.El Bojaddaini and Chatei [64] numerically investigated the effect of nonextensive parameters on sheath characteristics using the ion source term, which is assumed to be proportional to the electron density.El Bojaddaini [65] extended their work by considering two different types of ion source term, and compared the sheath results corresponding to each case.The above studies have not considered the influences of external magnetic fields, which are very common in plasma experiments and applications.In corona discharge, researchers used a magnetic field to enhance the discharge current and control the plasma [66-68].The study of a collisional sheath structure with nonextensive electrons becomes more complicated when considering the magnetic field magnetization effect.

In order to develop a more accurate model for the lowdensity plasma sheath in atmospheric-pressure discharge such as corona discharge and glow discharge, a generalized fluid model of the magnetized plasma sheath with thermal ions and nonextensive electrons is proposed in this work, in which collisional and source terms are considered.A modified Bohm sheath criterion is derived under the assumption of nonextensive electrons and used as a boundary condition to study the influences of the ion source term on the structure of the magnetized plasma sheath.In addition, the effects of ionization frequency, magnetic field and other parameters on sheath properties are studied and compared with a non-source plasma sheath model.In section 2, a generalized fluid model for a magnetized collisional plasma sheath containing nonextensive electrons and an ion source term is presented, and the corresponding form of the modified Bohm criterion is also derived.The numerical simulation results and discussion are presented in section 3,and finally a brief summary is given in section 4.

2.Fluid model and Bohm criterion

For a low-density discharge plasma in atmospheric pressure,the plasma density range is about 1014- 1 015m-3for corona discharge and 1016- 1 018m-3for glow discharge, and the electron temperature is around 1-5 eV.Assuming that the plasma density is about 1014- 1 016m-3at the plasma-wall interface, then the Debye length is aboutλD≈ 10-3- 10-4m,and the sheath scale is about 10-2- 10-3m.Assuming that the sheath thickness is much smaller than the scale of the bulk plasma and planar wall,the spatial coordinates can be reduced to one dimension along the x direction.Since the magnetization of ions is considered in the sheath model, the threedimensional velocity phase space(υx,υyandυz)is introduced.The sheath region is located betweenx=0 (the plasma edge)andx=xw(the planar wall), as shown in figure 1.The uniform magnetic field with an oblique angleθ(corresponding to the x axis)lies in the x-z plane,which is expressed asB=B(cosθex+ sinθez),where B is the magnitude of the magnetic field.

Figure 1.Schematic geometry of the magnetized plasma sheath model.

By introducing the Tsallis statistical theory,the electrons in the sheath are assumed to obey the q-nonextensive distribution functionfe(x,υe)shown in equations (3a) and (3b), and the electron density can be derived as equation (3c) [5, 44, 63]:

wherene0is the electron number density at the sheath edge andTeis the electron temperature,qis the nonextensive parameter which defines the degree of nonextensivity,e is the electron charge, andφis the electric potential in the x direction (normal to the wall).The potential in the sheath region is determined by the Poisson’s equation:

where0εis the vacuum permittivity.According to the plasma quasi-neutrality condition, the electron density at the sheath edge (x= 0) satisfiesne0=ni0=n0,whereni0is the ion number density at the sheath edge.For the steady-state sheath,the thermal ion satisfies the continuity and momentum equations

whereυi,mi,niandTiare the velocity, mass, density and temperature of the ions, respectively;νiis the collision frequency between the ions and neutrals; andSiis the ion source term.

The assumption of the ion source term function has a substantial impact on the sheath features.The simplest hypothetical ion source term assumes that the ion-electron pairs are created at a constant rate.This constant ion source term can be expressed as [28]:

wheren0is the plasma density at the sheath edge andτis the average time between two adjacent ionizations.Such a constant ion source could represent an external ionization mechanism, such as neutral atoms ionized by the uniform radiation [28], or could represent a photoionization mechanism due toγ-rays[69].Another form of the ion source term is based on the assumption that the ions are created by ionization of neutral atoms due to electron collisions.Thus,the source term is proportional to the electron density[28,64].Since the electrons are assumed to be q-nonextensive distributed in the model, according to equation (3c), the source term can be expressed in the following form:

The ion source term proportional to the electron density has also been used by the authors who studied the plasma sheath for the steady state [64, 65].The third ion source term considered in this work is written by the following expression[28, 38]:

where H represents the Heaviside function.Such a source term is called the cosine source term or Heaviside source.This kind of source term is artificially constructed to control the ionization rate with the ion flux velocity.If the flux velocity reaches acoustic speed, the ionization becomes zero and then remains zero in the plasma sheath.

In order to solve the aforesaid fluid model equations(4)-(6),some normalized dimensionless variables are introduced:Φ =eφ/ (kBTe),ξ=x/λD,ui=υi/cis,Ni=ni/n0,Ne=ne/n0,T=Ti/Te,σi=λD/(cisτ),ϵ=λDνi/cis,ωi=eB/mi,ωpi=andβ=ωi/ωpi, whereλD= [kBTe/ (ne0e2)]1/2is the Debye length,is the ion acoustic velocity,iσis the normalized ionization frequency,ϵis the normalized collision frequency,andωiandωpiare the ion cyclotron frequency and plasma frequency,respectively. Since we assume that the bulk plasma and wall are infinity in the y and z directions, thus the physical properties change only in the x direction, i.e. ∇= ∂/∂x.Substituting the above dimensionless variables into equations (4)-(6), the following normalized governing equations are obtained:

where A and D are variable coefficients that depend on the kind of ion source term:whenSi=0,A= 0andD=Niνiτ;whenSi=,A= 1andD= 1 +Niνiτ;whenSi==f( Φ)andD=f( Φ) +Niνiτ,wheref( Φ) =and whenSi==f(uix)andD=f(uix) +Niνiτ,wheref(uix) = cos (πuix/2)H(cis-cisuix).By multiplying Poisson’s equation (10) with∂Φ /ξ∂ and integrating over the sheath region, it can be obtained as

Submitting equations (11)-(13) into equation (17), the modified Bohm sheath criterion can be derived.Furthermore,utilizing the condition that ∂uix/∂ξ≥0at the sheath edge,one can obtain an upper limit Mach number for Bohm velocity in the collisional sheath; similar treatments have also been applied in several previous studies[21,57,70,71].This kind of upper limit result has not been fully comprehended by researchers, and the authors believe that it is related to the right-hand-side terms in equation (13), which are neglected in the traditional sheath model, i.e.the magnetization of ions,ion temperature,collisional force and ion source term.From equations (12) and (13), considering the boundary conditions at the sheath edgex=0,Φ →0,Ni→1,∂Φ /∂ξ= -E0≠0,one can have

whereMi=is the velocity allowed for ions to enter the sheath edge in units of Mach number, andE0is the normalized electric field at the sheath edge.By substitutinginto equation (18), it can be obtained that

According to equation (11),

Substituting equations (19), (20) into equation (17),

The lower limit Mach number of Bohm velocity is obtained by solving equation (21):

At the edge of the sheath,the electric field is positive and the ions are accelerated into the sheath region; therefore,∂uix/∂ξ≥0,anduix=uix0=Mi,uiy=uiy0,according to equation (13):

At the edge of the sheath, the change in ion density is small,and the ion temperature is much lower than the electron temperature, so equation (23) becomes

The ions are accelerated in the pre-sheath region between the plasma and the sheath, so the electric field in the pre-sheath region cannot be ignored;E0= -∂Φ /∂ξis the normalized electric field at the sheath edge.The magnetic field B in the xz plane and the nonzero electric field in the x direction result in anE×Bdrift velocity in the y direction asuiy0= -E0sinθ/β.Substitutinguiy0into equations(22)and(24), one can derive

C1andC2are coefficients for differentSi:whenSi= 0,C1=0 andC2=νiτ; whenSi≠ 0,C1= 1andC2= 1 +νiτ.Equation (25) is the complete form of the modified Bohm criterion for a collisional magnetized sheath with nonextensive electron distribution and an ionization source term.It is shown in equation(25)that the lower limit Mach number of the Bohm criterion depends on the nonextensive parameter q, collision frequency, ion temperature and angle of the magnetic field, and is independent of the magnitude of the magnetic field, whereas the upper limit is related to the parametersE0,θ,ϵandσi.This derived formula is consistent with several limiting cases with simplified conditions.For example, whenθ→0, equation (25) reduces to

This expression is agreed with the Bohm criterion in the unmagnetized sheath case obtained by El Bojaddaini and Chatei[65].Forθ→0,σi→ 0andϵ→ 0,the Mach number of the Bohm criterion for an unmagnetized collisionless sheath has only the lower limit, so equation (25) appears as

When the ion thermal temperature is ignored (T→0 ), the Bohm criterion for a nonextensive electron plasma sheath iswhich is in agreement with results reported by Gougam and Tribrche [72].Finally, for the case in whichθ→0,σi→ 0,ϵ→0,T→0,andq→1,equation (25) reduces to the classical Maxwellian sheath Bohm criterion:Mi≥1[3].

3.Numerical results and discussion

3.1.Bohm criterion characteristics

The Bohm criterion determines the ion velocity at the sheath edge, which acts as a critical condition for sheath structure.Figure 2 shows the variation of the modified Bohm criterion with the nonextensive parameter q for different ionization frequencies, collision frequencies, magnetic field angles and ion temperatures.The trend of the Mach numberMiin figure 2(a) shows that with growing ionization frequencyiσand collision frequencyϵ,the lower limit Mach number of the Bohm criterion keeps decreasing, which means a lower requirement of the ion velocity to enter the sheath domain.For low values of ionization frequency and collision frequency,Midrops gradually with increasing q,which could be related to the characteristic of the nonextensive distribution.As q takes a high value, there are fewer high-velocity electrons in the sheath [47], the average velocity of electrons is relatively slow,and the electron flux to the wall decreases.In order to maintain the stability of the sheath,the ion flux at the wall also decreases.According to the continuity equation of ions, the ion velocity entering the sheath boundary is also reduced.As can be seen from figure 2(b),the Mach number of the Bohm velocity decreases with an increase in the magnetic field angle and, in contrast, increases as the ion temperature increases,indicating that as the magnetic field angle is small,and the ion temperature is high,it is more difficult for the ions to enter the sheath.

Figure 2.Lower limit of modified Bohm velocity as a function of the nonextensive parameter q.(a) Different values of the ionization frequency σi and collision frequency ϵ, θ = 30 °, T = 0.1;(b) different values of the positive ion temperature T and magnetic field angle θ,σi = 0.01, ϵ=0.1.

Figure 3 shows the influences of ionization frequency and magnetic field angle on the Mach number range of Bohm velocity values for different collision frequencies.The colored area shows the possible Mach number value for different parameters.The solid lines in figures 3(a) and (b)represent the lower limit of theMi,and the dashed lines represent the upper limit of theMi.It can be seen in figure 3(a) that the possible range ofMiis larger when both the collision and ionization frequencies are low.When the ionization source is relatively large, the ion density in the sheath becomes substantial and the requirement for sheathside ion flux decreases, resulting in a relatively low ion velocity and a reduction ofMito a small fixed range.Figure 3(b) shows a similar but gentler trend ofMiwith increasing magnetic field angle.The change rate of the Bohm velocity grows but the possible range narrows as the magnetic field angle increases.The upper limit value in figure 3 verifies that the maximum value ofMiis affected by the parameters and becomes smaller when the collisional parameter or ionization frequency is higher,which is due to the increase in the right-hand-side terms of equation (6),and when the magnetic field angle is larger, the magnetization of the ions in the x direction becomes significant and the magnetic force grows higher, which also leads to a greater restriction of the upper limit value ofMi.

Figure 3.Influences of ionization frequency and magnetic field on the value range of the Bohm velocity.(a) Infulences of ionization frequency, θ = 30 °, q = 0.8;(b) influence of magnetic field angle,ϵ = 0.1,q =0.5.

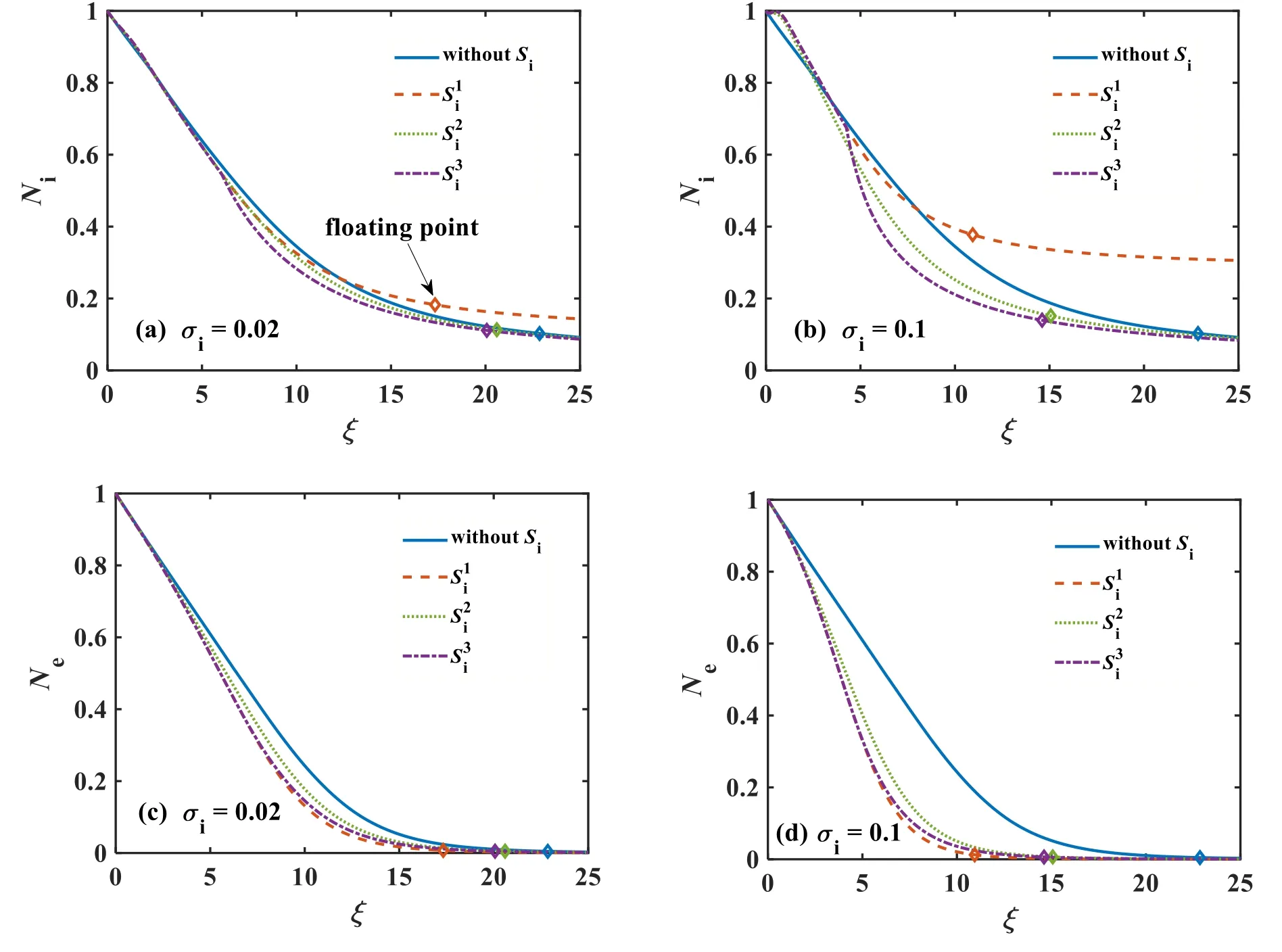
Figure 4.Charged particle density profiles for different source terms; rhombus markers indicate the sheath thickness when the plasma is adjacent to a floating wall,θ = 20 °, ϵ= 0.134, q = 0.7.(a)Ion density profiles when σi = 0.02;(b)ion density profiles when σi = 0.1;(c)electron density profiles when σi = 0.02;(d) electron density profiles when σi =0.1.

Figure 5.Variation of potential profiles for different ion source terms; rhombus markers indicate the sheath thickness when the plasma is adjacent to a floating wall,θ = 20 °, ϵ= 0.134, q = 0.7.(a) Potential profiles when σi = 0.02;(b) potential profiles when σi =0.1.

3.2.Particle density and potential distribution

In order to investigate the whole region properties of the magnetized sheath with ion source terms, differential equations (10)-(15) are solved numerically using the (4-5)th Runge-Kutta method,the absolute and relative error tolerance are set to 10-6,and the grid length for each step is about 0.01 Debye length to ensure numerical accuracy and stability.The physical parameters adopted in this work are as follows:n0= 5 × 1014m-3,Te= 5 eV,andmi= 40 amu (argon plasma).There is a presheath between the bulk plasma and the sheath edge, and a slowly changing potential at the edge results in a small electric field of which the normalized value is set asE0=0.1.

Figure 6.Profiles of space charge density for different source terms; rhombus markers indicate the sheath thickness when the plasma is adjacent to a floating wall,θ = 20 °, ϵ= 0.134, q = 0.7.(a) Profiles of space charge density when σi = 0.02;(b) profiles of space charge density when σi =0.1.

Figure 7.Profiles of sheath potential for different collision frequencies, magnetic field inclination angles and ion temperatures,q =0.6, σi = 0.02.(a) For different values of the collision frequency, θ = 20 °, T = 0.01;(b) for different values of the magnetic field inclination angle,ϵ = 0.1,T = 0.01;(c)for different values of the ion temperature,ϵ = 0.01, θ= 30 °.

Figure 4 shows the variation of charged particle density with the normalized distance of the sheath edge corresponding to different ion source termsSiwhen the ionization frequencies are 0.02 and 0.1 respectively.It is shown in figures 4(a)and(b)that the ionization frequency significantly affects the ion density distribution.When the ionization frequency value is 0.02, the variation trends of ion density corresponding to the proportional source term and the cosine source term are almost the same as in the non-source case,while the ion density distribution with a constant source term gradually deviates away from the zero source term.The rhombus markers on the lines indicate the position where the sheath reaches the floating wall, where the electron flux equals the ion flux:Ie+I0= 0.The electron flux is calculated byIe=and the ion flux is calculated byIi=nivix,the correspondingξvalue indicates the sheath thickness when the plasma is adjacent to a floating wall.The floating points in figure 4(a)shows that the sheath thickness becomes smaller when considering ion source terms.The additional ions in the sheath accelerate the establishment process of electric shielding, resulting in a shorter sheath.As shown in figure 4(b), when the ionization frequency is 0.1,the influence of different ion source terms on the ion movement in the sheath region becomes more obvious, resulting in a significant difference in ion density distributions.When the ionization frequency is fixed, the ion density profiles differ from each other; since the ionization is uniform through the sheath for theSi1source(red line),the ion density is distinctly larger, which means that the ionization source plays an important part in forming the sheath.Figures 4(c) and (d) show the variation of electron density distribution corresponding to different source terms.The electron density distribution with source terms decreases more rapidly in the sheath region.Since the ionization process consumes high-velocity electrons, the electron flux towards the wall becomes lower.Figure 4(c) shows that when the ionization frequency is small,the electron density distribution corresponding to the zero source term is similar to the nonzero ones.As can be seen from figure 4(d),with an increase in ionization frequency,the ion source term significantly affects the electron motion in the plasma sheath, and the electron density distributions corresponding to nonzero source terms are gradually separated.

Figure 5 shows the trend of sheath potential with normalized distance for different ion source terms when the ionization frequencies are 0.02 and 0.1 respectively.Compared with the zero source term, the sheath potential corresponding to the nonzero source terms drops more rapidly; that is, the sheath electric field is larger.The sheath potential corresponding to the constant source term (Siα)decreases fastest.Figure 5(b) shows that as the ionization frequency increases, the influence of ion source terms on the sheath potential becomes more significant.The floating point in figure 5 shows that for nonzero cases, the floating wall potential increases obviously with an increase in ionization frequency, and the sheath thickness decreases when the ionization frequency increases.This phenomenon may be related to the deceleration of electrons by the electric field of the sheath,which is mainly distributed on the edge side of the sheath, where most of the ionization occurs.Then, the increase in ionization frequency leads to a decrease in the ion velocity and causes ion aggregation at the edge of the sheath.Therefore,the space charge density of the sheath is enhanced,the sheath thickness is shortened, and the sheath potential increases.

Figure 6 shows the evolution of the sheath space charge density distribution overξfor different ion source terms.It is obvious that the profile of space charge density for the zero source term is lower than those for the nonzero source terms.When the plasma sheath takes a constant ion source term, the peak value of the space charge density is largest.As the ionization frequency increases, the peak values of space charge density corresponding to the three nonzero source terms increase.In addition, the space charge density at the wall corresponding to the proportional and cosine source term coincides with the zero source case, but the charge density for a constant source term is higher than those for the above cases,which is consistent with the results in figure 4.

Figure 7 shows the effects of collision frequency,magnetic field angle and ion temperature on the sheath potential.Figure 7(a) shows that the sheath potential drops faster when the collision frequency takes a lower value, and the absolute value of the floating wall potential declines, but the floating sheath thickness changes only slightly, and the influence of the collision force on the sheath width is estimated to be small.As shown in figure 7(b),by increasing the magnetic field angle,both the sheath potential and the sheath thickness increase, but the final floating wall potential changes only slightly.Figure 7(c) shows that the effect of ion temperature on the sheath profile is small while it is much smaller than that of electrons, and for thermal plasma, the sheath potential decreases and the sheath thickness becomes narrower.

3.3.Ion velocity and sheath thickness

Figure 8 shows the variation of ion velocity in three directions with the normalized distance corresponding to different ion source terms.It is shown that the ion source terms have great influences on the ion velocity in the sheath.As can be seen from figures 8(a) and (b), with increasing ionization frequency, the ion velocity in the x direction at the sheath edge decreases, which is consistent with the results obtained in figure 2.In the sheath region, the ion velocity in the x direction corresponding to the nonzero source term increases rapidly compared to that in the zero source case.When the system takes a constant ion source term, the ion velocity in the x direction changes the fastest.

Figure 8.Variation of ion velocity in three directions for different ion source terms,θ = 20 °, ϵ= 0.134, q = 0.7.(a) Ion velocity in the x direction when σi = 0.01;(b) ion velocity in the x direction when σi = 0.1;(c)ion velocity in the y direction when σi = 0.01;(d)ion velocity in the y direction when σi = 0.1;(e)ion velocity in the z direction when σi = 0.01;(f) ion velocity in the z direction when σi =0.1.

As can be seen from figures 8(c) and (d), the growth trend of ion velocity in the y direction corresponding to the nonzero source term transforms more rapidly compared with the zero source case, which is more obvious with an increase in ionization frequency, and the growth trend is similar near the sheath edge.As can be seen from figures 8(e) and (f),compared with the ion velocity in the z direction corresponding to the zero source term, when the ionization is remarkable,whenSi=the change trend of ion velocity in the z direction is gentler.

Figure 9 shows the influences of plasma parameters on the floating sheath thickness for different ion source terms.Figure 9(a) shows that when the ionization source is not considered, the sheath thickness is sensitive to the magnetic field angle,and the thickness grows with collision frequency.Figures 9(b)-(d) also show that the collision frequency has little effect on the sheath thickness when considering an ion source term, except when the source term isSi2.The ionization rate has a significant impact on the sheath thickness.In general, the ionization source shortens the sheath width with extra ions to accelerate Debye shielding.Under the same conditions,the sheath with a proportional source term has the largest thickness, and the case of a constant source term has the shortest 11λD,which is much shorter than the case of a zero source term.

Figure 9.Contours of sheath thickness for different ion source terms, q =0.7.(a)Si = 0;(b)Si = 20 °; (c)S i == 20 °;(d) = 20 °.

4.Conclusions

In this work, a magnetized collisional plasma sheath model with nonextensive electron distribution and ionization source terms is established to investigate the sheath properties in atmospheric-pressure discharge with low plasma density.An extended form of the Bohm criterion with an upper limit is derived, governed by the ionization frequency, ion-neutral collision frequency, magnetic field angle, ion temperature,and nonextensive parameter q.Taking this modified Bohm velocity as the boundary condition, the sheath fluid model is numerically solved and the effects of the ion source and other considered terms on the magnetized plasma sheath properties are investigated.The results show that in low-density plasma discharge with atmospheric pressure, the influences of ion source terms on sheath properties are obvious and become significant with increasing ionization frequency.Other parameters like elastic collisional frequency between ions and neutrals, magnetic field angle, and ion temperature also play important roles in establishing the sheath structure.As the ionization frequency increases, the Bohm velocity decreases and the Mach number range of the Bohm velocity narrows.The upper limit Mach number of the Bohm velocity is derived in this model and analyzed to be related to the collision force and ion source term.The sheath thickness becomes smaller when the ion source term is considered;the additional ions in the sheath accelerate the establishment process of electric shielding, resulting in a shorter sheath.In addition, ion-neutral collisions, magnetic field angle and ion temperature also significantly affect the sheath potential, space charge density and sheath thickness.Both the ionization and ion-neutral collisions have essential effects on the sheath properties.When the ionization frequency increases,the influence of ion source terms on the sheath potential becomes more significant.The sheath potential drops faster when the collision frequency takes a higher value, but the floating sheath thickness varies little with the collisional parameters.

Acknowledgments

This work was supported by National Natural Science Foundation of China (Nos.11975062, 11605021 and 11975088) and the China Postdoctoral Science Foundation(No.2017M621120).