Relativistic toroidal light solitons in plasma

Zhongming CHENG (程中明), Dachao DENG (邓达超),Mingyang YU (郁明阳) and Huichun WU (武慧春),*

1 Institute for Fusion Theory and Simulation, School of Physics, Zhejiang University, Hangzhou 310027,People's Republic of China

2 College of Engineering Physics,Shenzhen Technology University, Shenzhen 518118,People's Republic of China

Abstract In the laser-plasma interaction, relativistic soliton formation is an interesting nonlinear phenomenon and important light mode convection in plasmas.Here, it is shown by threedimensional particle-in-cell simulations that relativistic toroidal solitons, composed of intense light self-consistently trapped in toroidal plasma cavities, can be produced by azimuthallypolarized relativistic laser pulses in a near-critical underdense plasma.

Keywords: azimuthally polarized laser pulse, near-critical underdense plasma, toroidal solitons,relativistic solitons in plasma, 3D particle-in-cell simulation, self-focusing in plasma

1.Introduction

The relativistic-laser interaction with plasma can generate radiations in the microwave to gamma-ray range, high-energy electrons and ions in the MeV to GeV range, as well as form relativistic solitons with extreme fields and plasma currents [1].Compared with light solitons in optical fibers [2], relativistic solitons in plasma are highly nonlinear and can propagate slowly or even be at rest[3].Relativistic solitons have been investigated analytically [4-10], numerically by particle-in-cell (PIC) simulations [11-17], and experimentally [18-22].

Two-dimensional (2D) PIC simulations [11-14] have shown that circular shaped s-type solitons formed in the laserplasma interaction can be robust and stable[13].The laser field in the s-soliton is trapped in a cylindrical plasma cavity and has a half-cycle standing wave mode.When propagating in plasma,the laser pulse loses energy, accompanied by a downshift in its frequency.For plasma density close to the critical density,much of the laser energy will be trapped in the cavity created by the ponderomotive-force expelled electrons,forming a soliton that is almost at rest.At longer times,plasma ions in the cavity are dug out by the charge-separation field,and the cavity becomes quasineutral, forming the so-called postsoliton.Similarly, p-type solitons can be formed by p-polarized lasers [11, 17], and are less stable than the s-solitons.The latter are more robust because their electric fields are always parallel to the plasma boundary,resulting in much weaker laser-plasma coupling and heating.However, s-solitons seem to only exist in 2D space.

Three-dimensional (3D) PIC simulations [15] show that relativistic solitons can have properties of both s-type and p-type solitons, but their postsoliton evolution is more like that of the p-type solitons.Moreover, circularly polarized laser pulses can form relativistic solitons that emit spiral electromagnetic waves [16].In the postsoliton stage, the trapped laser electric field can also efficiently heat the plasma by vacuum heating [23, 24], leading to an implosion of the plasma cavity [13].Experiments have confirmed the postsoliton stage of such relativistic solitons with circular plasma cavities[19-22].In particular,Sylla et al[21]observed a train of ball-shaped postsolitons in the wake of the laser pulse.Several potential applications of these solitons have also been proposed, such as for ion acceleration [7] and attosecond pulse generation [25, 26].

As discussed above, in the postsoliton stage these 3D solitons behave like p-type [15], especially because there are always electric field components perpendicular to the inner surface of the 3D plasma cavity.Here,we propose an s-typelike 3D soliton with its electric fields always tangential to the inner surface of the plasma cavity.This can be accomplished by a torus plasma cavity, with the confined electric fields along the torus boundary.Such a laser-plasma configuration can be realized by an azimuthally-polarized laser, with a toroidally distributed and directed electric field, propagating in underdense plasma.A toroidal plasma cavity is then selfconsistently produced by the pondermotive force of this doughnut-like laser pulse.

2.Simulation setup

To verify our scheme, we carry out 3D PIC simulations by JPIC3d, which adopts a direct-splitting algorithm [27] to solve the Maxwell equations.This Maxwell solver is free of numerical dispersion along three xyz axes.An azimuthallypolarized laser pulse can be generated by several optical techniques[28].Its electric field along the azimuthal directionis given by

The laser pulse propagates in the x direction and focuses on the surface of a uniform plasma slab.The ion-to-electron mass ratio of the plasma is mi/me=1836.The simulation cell is cubic,of size(0.05λ)3and contains eight quasiparticles per cell.The time step is 0.05λ/c.The boundary conditions are periodic along the y and z axes and absorbing along the x axis for both fields and particles.

3.Results and discussion

Figure 1 shows the propagation of an azimuthally-polarized laser pulse with normalized field strength a0=eE0/mecω=0.84 (corresponding to intensity I ～1.15×1018W cm-2for the 1 μm wavelength laser light), w0=3λ and T=1λ/c in underdense plasma of initial density n0=0.3nc, where meis the electron rest mass, c is the light speed, and ncis the critical density.The laser pulse starts from the left boundary at x=0 and focuses on the plasma surface at x=2λ.In the x-y plane, the electric field along the z direction is s-typelike.The pulse contains about two light cycles and undergoes self-focusing in the plasma region x ∈[2λ, 26λ].The selffocusing is due to relativistic mass variation and electron expulsion by the pondermotive force [29, 30].With increasing field strength, the toroidal laser beam shrinks in the transverse direction.In the underdense plasma, a ringdistributed plasma wave is generated in the wake of the laser pulse.Such plasma wakefields are nonlinear and have a curved wavefront [31].

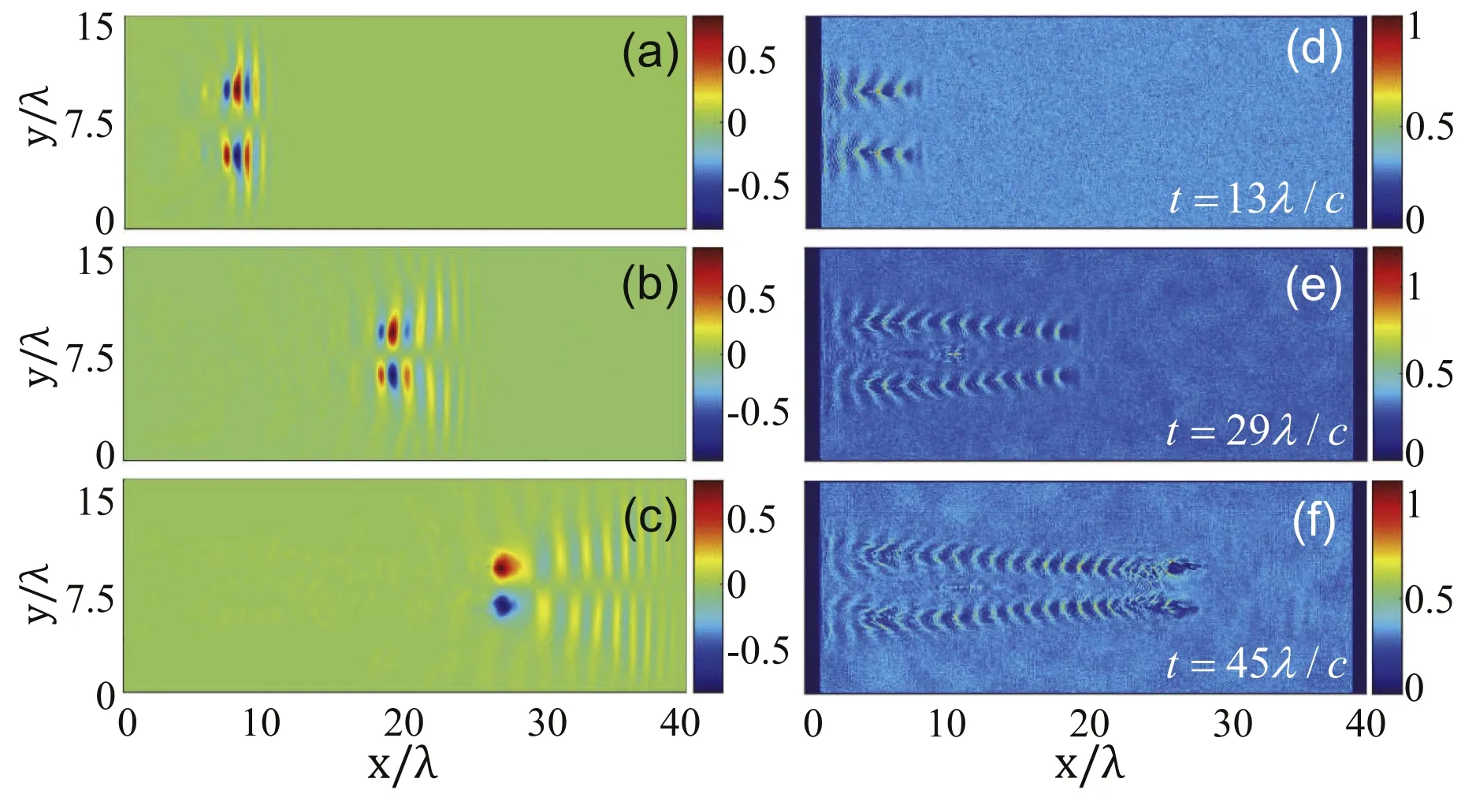
Figure 1.Evolutions of electric field and electron density from 3D PIC simulation for a0=0.84, n0=0.3nc, w0=3λ and T=1λ/c.Snapshots of eEz/mecω (a)-(c) and ne/nc (d)-(f) in the x-y plane are taken at t=13λ/c, 29λ/c and 45λ/c, respectively.

With energy loss of the driving laser,its frequency decreases continuously due to photon number conservation [32].The background plasma frequency is～0.55ω.When the laser frequency decreases with ω →ωpe, the group velocityof the laser light vanishes and mode conversion occurs.An intense standing light wave is created,forming a toroidal electron cavity that in turn traps the laser at x ～26.5λ, as seen in figures 1(c) and (f).The laser ponderomotive force continues to act on the plasma electrons at the cavity boundary and gradually widens the cavity.On the time scaleof ion motion, the intense chargeseparation field in the cavity expels the plasma ions until it becomes quasi-neutral, and the soliton enters the postsoliton stage.The light electric field is along the azimuthal direction at all times,so that it is oppositely directed in the upper and lower cross-sections of the 2D view in figures 1(a)-(c).

Figure 1 shows that a toroidal s-type soliton can be formed by an azimuthally polarized laser pulse.The formation process is effectively adiabatic with gradual energy loss and frequency redshift.One can also enhance soliton formation by increasing the plasma density.Figure 2 shows a much faster formation process for a0=0.8 and n0=0.7nc,with the other parameters same as in figure 1.In this case,the plasma frequency is ωpe～0.84ω, closer (than the preceding case) to the central frequency of the two-cycle laser pulse.Actually, the two-cycle laser pulse itself has a significant portion of energy spanned into the band of 0.84ω.Thus, the focusing laser pulse can form the electron cavity and gets self-trapped within a shorter propagating distance[33].In fact, figure 2 shows that in a short propagation distance of ～3λ,about 35%of its energy is already trapped by the toroidal electron cavity.This nonadiabatic formation process is more efficient than the case in figure 1,since less light energy is spent driving the plasma wave in the propagation process.

Figure 2.Nonadiabatic relativistic toroidal soliton formation for a0=0.8,n0=0.7nc,w0=3λ and T=1λ/c.Snapshots of eEz/mecω(a)-(c)and ne/nc (d)-(f) in the x-y plane are taken at t=10λ/c, 20λ/c and 30λ/c, respectively.

Figure 3 presents the electric field amplitudeE=and electron density in the transverse y-z plane(x=4.4λ)for the soliton in figure 2.We see that the scenario is consistent with that of ring soliton formation.Figures 3(a),(d) and (g) at t=15λ/c show a balance between the chargeseparation potential and laser ponderomotive forces, where more than half of electrons have been evacuated in the cavity,but ions still remain unmoved.At t=30λ/c in figures 3(b),(e) and (h), 100% electrons and ＞50% ions are evacuated within the cavity.Ion evacuation lags a bit behind electrons because of their different masses and evolving time scales.Arrows in figure 3(e)mark the direction of the ponderomotive force-(e2/2meγ)∇A2[34]of the soliton fields,where A is the laser vector potential and γ is the relativistic factor of electrons.After t=35λ/c,ions are almost completely evacuated,and the soliton becomes a postsoliton.In this stage, the ponderomotive force continuously pushes the toroidal plasma cavity to expand inward and outward.Figures 3(g)-(i) show that the central plasma column is compressed gradually with increasing density.The plasma density around the column rim is overdense with ne＞4nc.

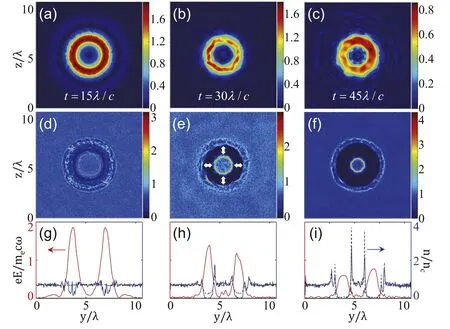
Figure 3.Transverse distribution of relativistic toroidal soliton in figure 2.Snapshots of eE/mecω(a)-(c)and ne/nc(d)-(f)in the y-z plane are taken at t=15λ/c,30λ/c and 45λ/c,respectively.Here, E = .Lineouts of E,ne and ni(dashed line)(g)-(i)along the y direction at z=5.33λ for the same moments.One can clearly see laser-light trapping in the toroidal plasma cavity.

Figure 4 plots the electric and magnetic field vectors for the soliton in figure 2.We see that the electric field is azimuthally continuous in the whole toroidal plasma cavity.The electric fields in figures 4(a) and (b) correspond to two adjoining antinodes around t=30λ/c(see figures 3(c)and(f)),and their directions are opposite.Within the toroidal cavity,the electric field is tangential to the cavity boundary, so that its interaction with the plasma is weak.The vortex magnetic fields in figures 4(c) and (d) always perpendicular to the toroidal electric fields.This field distribution is the same as the s-type soliton in 2D space [33].

Figure 4.Vectors of electric fields((a)and (b))in the y-z plane and magnetic fields((c)and(d))in the x-y plane for the soliton in figure 2 at t=29.6λ/c((a)and(c))and 30.4λ/c((b)and(d)),respectively.

Figure 5 shows the electric field Eyoscillation and the corresponding power spectrum in the soliton.The oscillation central frequency is about 0.66ω, which is less than the plasma frequency ωpe～0.84ω of the background plasma, so that the electromagnetic field can be stably trapped by the cavity.For the postsoliton stage after t=35λ/c, the light frequency further decreases as the laser energy is spent in widening the cavity.

These toroidal solitons should be close to a fundamental resonant mode without any nodes in an ideal toroidal cavity[35].According to [35], the resonant angular frequency is given approximatively by 2.5c/rm, where rmis the radius of the so-called minor cross section of the toroidal cavity(i.e.the radius of the circular plasma channels in figure 2(f)).There are rm⋍0.46λ and 0.69λ for the plasma cavities in figures 3(e) and (f), respectively.The estimated resonant frequency is in the range of [0.58ω, 0.86ω], which can cover the spectral peak in figure 5(b).

Figure 5.Temporal evolution (a) and frequency spectrum (b) of electric field component Ey recorded at x=4.55λ, y=5λ,and z=6.5λ.

The stability of our toroidal solitons is quite robust,mainly because the contained electric field is tangential to the inner surface of the cavity with much less plasma heating.In our simulations,we observe the stable soliton up to t=150λ/c, which always remains the same field topology structure as discussed above.This soliton should be stable for a much longer time.Due to the continuous push by radiation pressure of the soliton field, the outer diameter of the cavity expands from 4.2λ at t=30λ/c (figure 3(e)) to 6λ at t=150λ/c.Meanwhile, the central plasma column shrinks from 2.3λ to 0.6λ in width.The action done by the light pressure consumes the significant energy of the soliton field, which decreases to eE/mecω=0.04 at t=150λ/c.

To further justify the robust formation of these toroidal solitons, we have carried out simulations for wider parameters.For example, if the laser pulse duration is doubled to T=2λ/c with the other parameters unchanged, simulation shows that soliton formation occurs deeper in the plasma,namely at x ～11λ.This is because the pulse-intensity gradient(i.e.ponderomotive force)is much reduced and also the spectrum range is narrower for this longer pulse.On the other hand, if the laser amplitude is doubled to a0=1.6 with the other parameters unchanged, we found that multiple cavitations appear in the plasma,but eventually a complete toroidal soliton can still emerge.This scenario can be attributed to the much increased ponderomotive force that can lead to multiple local cavitations in the plasma.We also found that, by decreasing the plasma density with n0=0.5ncfor a0=1.6,the soliton formation process is similar to that of figure 1.

4.Conclusion

In conclusion, we have shown that relativistic toroidal solitons composed of half-cycle intense light self-consistently trapped in toroidal plasma cavities can be created by azimuthally-polarized relativistic laser pulses in a near-criticaldensity plasma.The light electric field is mainly tangential to the boundary of the toroidal plasma cavity, so that the direct light-electron interaction is minimal and the soliton can survive for a long time.These new-topology solitons open a new option for potential applications based on conventional relativistic solitons.

Acknowledgments

This work was supported by the Strategic Priority Research Program of Chinese Academy of Sciences(No.XDA17040502).