基于数字图像相关的切削加工剪切区应变率监测调控研究*
2023-03-15聂广超杨政彦张小明
赵 爽,张 东,聂广超,杨政彦,张小明
(华中科技大学,武汉 430074)
切削加工是航空制造领域的主要加工方式之一,航空发动机关键零件(如叶轮、叶盘)的切削加工质量影响着发动机的安全性与稳定性。切削应变/应变率不仅影响切屑种类的生成[1–2],而且决定已加工表面残余应力分布[3]、裂纹的产生与扩展。因此,实现加工过程应变/应变率的监控,对改善切屑形成和提升航空制造表面完整性具有重要意义。
通常采用应变片或引伸计测量应变,但是这种方法只能获取两点之间的应变大小而非全场信息。近年来,得益于数字图像相关 (Digital image correlation,DIC)技术的发展,基于高速相机的原位测量系统可以实现全场应变非接触测量[4–5]。
DIC算法最早在20世纪80年代被提出,经过国内外学者的完善,如今已经较为成熟[6–8],被广泛应用在材料学[9]、机械科学[10–11]、土木工程[12–13]、航空航天[14]等领域。为了研究剪切区域应变与应变率,List[15]采用高速摄像系统观察低碳钢切屑并分析应变和应变率分布。Thimm[16]使用双帧相机研究了AISI 1045钢在不同切削速度、未变形切屑厚度和前角下的切屑形成和剪切应变率。Harzallah[17]使用双谱成像仪在正交切削中同时获得运动场和温度场,发现由于锯齿切屑形成的循环性质,高应变率区域在空间中是固定的,其值仅随时间略有变化。Davis等[18]研究了加工过程中切屑流动方向主变形区内的应变过程。Zhang[19]通过原位成像准确描述了加工过程中的剪切区应变–应力场演变行为,通过改变前角、切削速度和工件初始温度,获得了不同水平的应变/应变率。Bergs[20]利用高速DIC技术研究了主变形区的应变和应变率场。
DIC技术已广泛应用于切削加工过程,实现加工过程应变–应力场的表征。但是由于DIC算法计算过程耗时、对图片质量要求高等特点,目前很难实现对切削过程的应变/应变率实时监控。本文开发了一套切削过程原位成像系统,通过双帧相机获得切削剪切区数字图像,结合多线程全局数字图像相关算法,实时获取应变增量,并根据应变率大小反馈调节机床主轴转速,实现正交切削过程的应变率的在线监测和调控。
1 试验平台搭建
1.1 正交切削原位成像系统
如图1所示,在数控车床上搭建了一套正交切削原位感知系统,主要包括刀具、工件、光源和相机。工件通过一套高刚度的套筒夹具夹持安装在车床主轴上,槽刀刀片从工件的圆周处沿径向进给。
切削过程中,采用相机获取加工过程图片。为了保证拍摄效果,试验过程中未使用冷却液或润滑油。由于干式切削与常规冷却切削的状态接近[21],因而可以采用干式切削替代研究实际加工过程。另外也可以采用钢化玻璃限制切屑侧向流动以及切削液污染[22],从而实现对常规切削的在线观测。未变形切屑厚度为0.2 mm,初始主轴转速为60 r/min,在加工过程可通过改变主轴倍率(50% ~ 120%)调节实际转速;工件材料为AISI 1045,硬度测量值为HRA(51±1.5),厚度为3 mm,直径为230 mm;刀具由硬质合金制成,前角为15°,后角为7°。
相机型号为博科奥公司pco.pixelfly USB,该双帧相机以1 μs的帧间距进行两次曝光,从而获取加工过程中切屑形成过程的照片。相机配备了Navitar 12X光学镜头,放大倍数为6倍。光源为EverGreen 30 mJ激光光源,可独立产生两束光,两束光的间隔是图片的实际帧间距,试验中该间隔被固定为10 μs。
1.2 机床主轴自动调速系统
更改机床数控系统PLC梯形图使得机床可通过外部信号调节主轴倍率,控制信号由电脑通过控制板卡发出,控制板卡选用研华pci – 1245型号四轴脉冲型步进/伺服电机运动控制卡,使用数字量输出口作为机床倍率的信号输入。由于板卡的输出为低电平,需要通过一个继电器(YF – 38),将板卡的输出信号转化为一个高电压 (24 V),来作为机床的主轴倍率控制信号。
运动控制卡输出端子卡为ADAM-3952,控制4个轴的运动。在加工过程中,上位机根据剪切带应变率测量结果,通过控制板卡将主轴转速调节信号发送到机床PLC,从而改变机床的实际转速,达到设定应变率。
1.3 相机与光源同步触发系统
如图1所示,工件夹具附近安装了接近开关,主轴每转一周接近开关触发一次,从而保证在工件同一位置进行拍摄。由于工作过程涉及相机、光源、主轴控制信号和接近开关之间的协同配合,本文选用高精度延时触发器实现同步控制,控制时序如图2所示。

图1 正交切削原位成像系统Fig.1 In-situ imaging system for orthogonal cutting
图2中,texp1和texp2分别是相机两次曝光的时间;tif为相机帧间距,但是实际帧间距为光源发出两束光的时间间隔trif=texp1+tif。激光的闪烁时长极短,通常为十几纳秒,因而可以避免产生运动模糊。从相机接收到外部触发信号,到相机开始抓取一张图片,共有5.4 μs的时延,而激光光源从接收到信号到发出光束,有135 μs的蕴光时间。
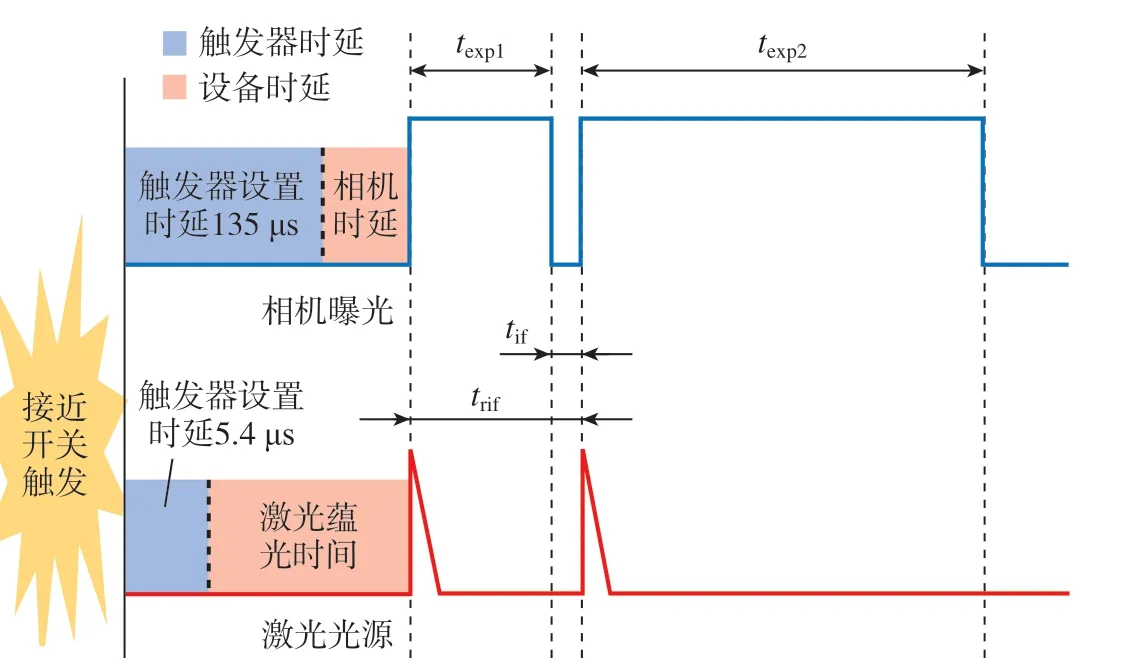
图2 相机与光源脉冲信号Fig.2 Pulse signal of camera and light source
1.4 剪切区应变率监控
为了协调系统各部分之间的工作,编写了应变率监控算法,软件主要包含4个模块,分别是DIC模块、相机交互模块、控制板卡交互模块和人机交互界面部分。
DIC模块主要完成数字图像相关计算,包括参数设定、运行过程中的位移场与应变场实时计算、结果保存和显示;相机交互模块主要负责与相机的各种交互,包括相机参数设定、图片采集、格式转换与保存、相机触发与DIC计算的同步控制;控制板卡交互模块主要负责与控制板卡的各种交互,包括控制板卡的初始化、向控制板卡发送控制指令驱使电机转动;人机交互界面部分主要负责与用户之间的交互,包括剪切区图片、应变率结果的显示。
剪切区应变率监控的完整工作流程可分为预定义阶段与工作循环阶段。预定义阶段主要为设备初始化、参数定义等;工作阶段是一个循环,不停重复着等待接近开关触发、获取双帧图片、分析图片、给出控制信息、调控加工参数步骤,如图3所示。两阶段详细介绍如下。
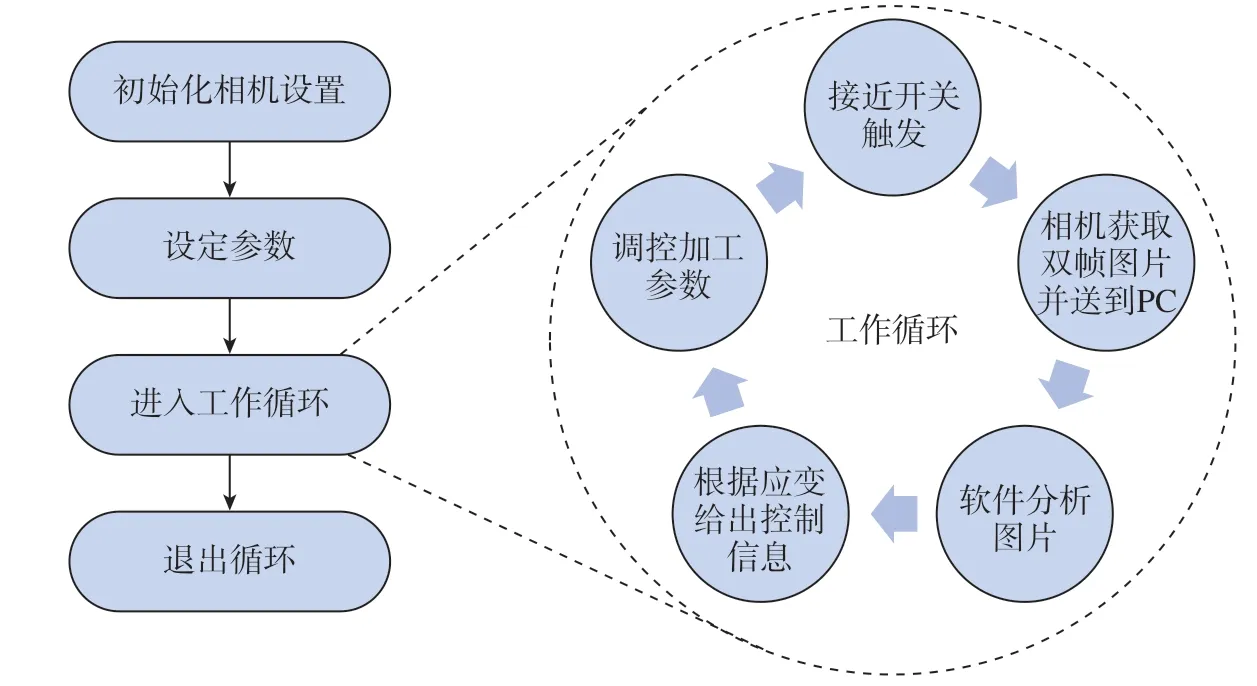
图3 剪切区应变率监控软件工作流程Fig.3 Workflow of strain rate monitoring software in shear zone
(1)预定义阶段。软件启动后首先连接相机,并将相机的触发模式设置为外部触发,获取方式为双帧模式,设定帧间距为1 μs,相机第1帧曝光时间为10 μs。此后手动进行一次软触发,获取两帧图片,这两帧图片中的刀具位置是后续选取第一剪切变形区为感兴趣区域 (Rigion of interest,ROI)的重要参考。随后设定ROI,并进行网格生成,继而在刀尖点前选择一条平行于前刀面的线段。切削区域应变率是不均匀的场量,沿着垂直剪切带方向是先增加后减小的,沿着剪切带方向是基本均匀的[23],本文测量的应变率是沿着垂直剪切带方向的应变率的最大值,近似用上述所选线段上的最大应变率表示。完成预定义阶段后的软件界面如图4所示。
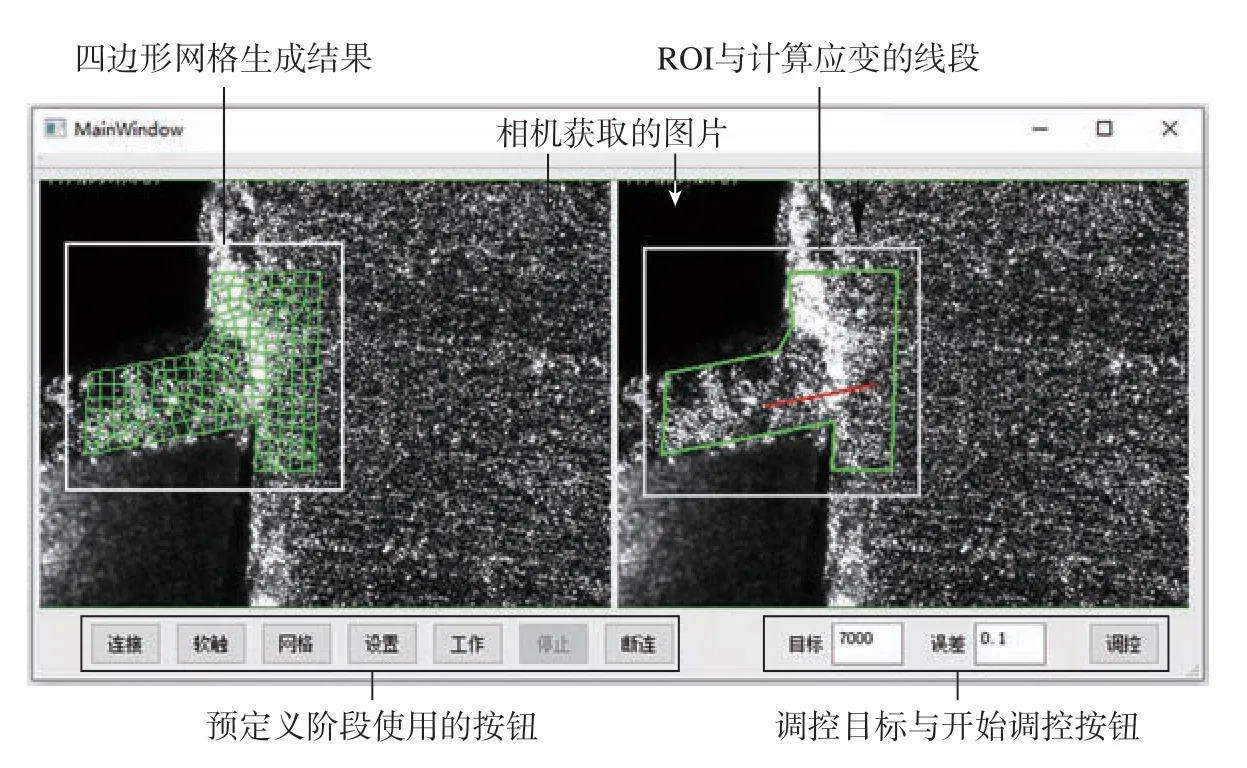
图4 完成预定义阶段后的人机交互界面Fig.4 Human - computer interaction interface after completing pre-definition stage
(2)循环工作阶段。在点击“工作”按钮后,软件进入监测状态,实时显示当前的应变率计算结果;在设置好调控目标后点击“调控”按钮,软件进入监控状态,开始监测应变并反馈控制信号。具体过程为:主线程调用获取图片的函数并阻塞等待,当接近开关触发并向相机发送触发信号,相机在激光配合下获得两帧图片,主线程继续进行图像处理,并完成数字图像相关计算与应变率计算。应变率调控方法采用了简单的单输入单输出模糊控制算法:当应变率高于预设值时,将机床主轴倍率降一档(10%),反之则升一档,如果处于可接受区间则不发出控制信号,即
式中,Es为设定应变率;E为当前应变率;e为允许的误差百分比。在主轴倍率没有达到上下限时 (主轴倍率最低50%,最高120%),新的主轴倍率Rnew等于原主轴倍率Rold加上反馈ΔR,即
图5展示了软件工作过程界面,其中,左下角的窗口展示了实时获得的两帧图片的剪切区位移场计算结果,右侧的窗口实时绘制从开始执行调控以来剪切区的等效应变率。软件的计算部分使用了5个线程并行处理,一次工作循环需要的时间为1~2 s。
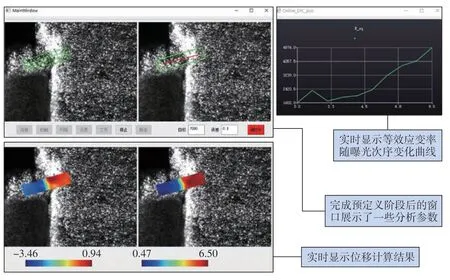
图5 剪切区应变率监控软件工作界面Fig.5 Working interface of strain rate monitoring software in shear zone
2 剪切区应变率实时计算
剪切区应变率监控软件的计算模块是系统的核心单元,双帧相机在获取一组照片后,需要通过DIC计算获得全场位移与应变信息。
2.1 全局数字图像相关分析方法
首先,基于区域分解方法[24]实现了用户定义的ROI四边形网格生成。其次,图片的相关性度量方法为图片灰度值差的平方求和,即
式中,F为用欧式距离表示的图片相关度;f(x)与g(x)分别为参考图片、变形图片上坐标x处的像素灰度值;通常对f和g作归一化处理。Q为四边形区域;x为一个落在Q区域内的像素的二维向量坐标;xwarp则是该像素在平移和变形后处于变形图片上对应的坐标位置。
式中,u、v是像素点沿水平、竖直方向的位移。采用四边形网格划分ROI后,四边形Q内任一像素点的位移均可以由四边形Q的结点位移向量pQ通过形函数插值获得。在全局DIC方法中,一次性考虑所有四边形网格节点位移,得到:
式中,S为整个被计算区域,由多个四边形单元构成;Q为单个四边形单元,在计算之前通过等参变换,将其映射为正方形单元[25]。构造全局节点位移向量p= [u1,v1,u2,v2,…,un,vn]T,表示整个网格中所有节点的位移大小,则有pQ=Gp= [uq1,vq1,uq2,vq2,uq3,vq3,uq4,vq4]T;G为由0和1组成的节点组装矩阵;向量p的解即为所求目标。令F导数等于0进行求解,即
采用牛顿–拉弗森迭代方法求解式(6),先假定p的初始值为p0,则有
其中
式中,pi为向量p的第i个分量。求得p的变化量Δp,更新p的值p=p0+ Δp,重复这个过程直到收敛,整个过程的实现如图6所示。
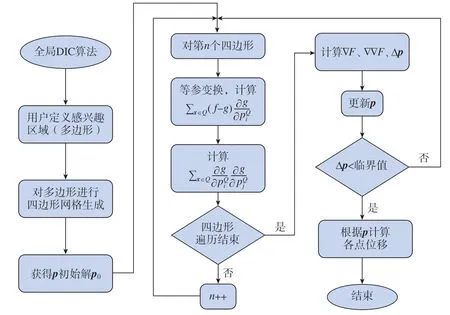
图6 全局DIC方法程序框图Fig.6 Program block diagram of global DIC method
2.2 数字图像相关并行处理与应变增量计算
从式(8)和(9)可以看出,在一次迭代中,需要计算所有在S范围内的四边形,耗时较久。本文采用并行计算提高计算效率。将由多个四边形组成的S拆分成若干个小的区域,分别处理每个小区域内的四边形,再将所有结果求和,如图7所示。
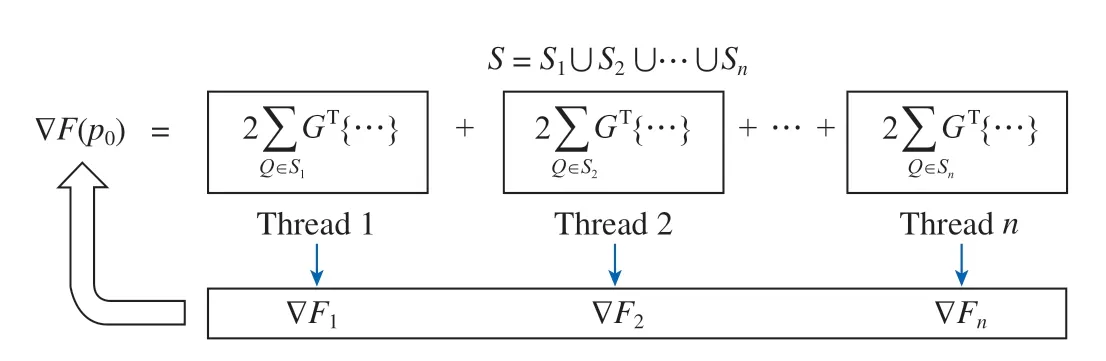
图7 数字图像相关并行处理示意图Fig.7 Schematic diagram of parallel processing of DIC
迭代收敛后,得到了所有网格节点的位移,再经过形函数插值即可得到ROI的全场位移。由于将计算中最耗时的求和过程分解成多线程并行计算,因此算法的分析效率有所改善,在采用5线程计算时,当分析区域大小为6 ~ 8万像素点时,获得全场位移所花费的时间为1 ~ 2 s;使用开源DIC软件包Ncorr进行相同大小区域的分析时,所花费时间为5 ~ 6 s[26]。
此外,为测试本算法计算位移的准确性,设计了一对已知全场位移分布的待分析图片,如图8所示,分别使用本算法与Ncorr软件包分析了图8(a)和(c)图片中间400×400像素大小的全场位移,并将结果与准确位移场图8(b)进行对比,误差Er =(Dc–Ds)/Ds,其中Dc是本算法或Ncorr软件包计算值,Ds是准确位移场图8(b)的值。图9给出了误差Er分布状况。
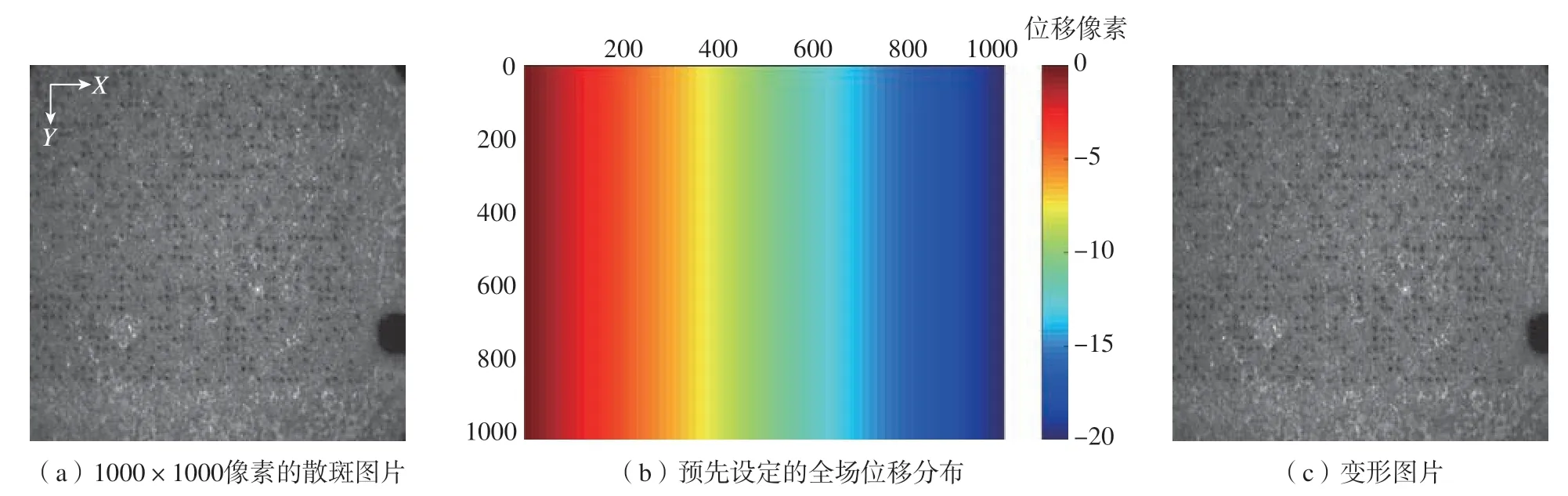
图8 用于测试算法的参考图片与变形图片Fig.8 Reference and deformation images for testing algorithm
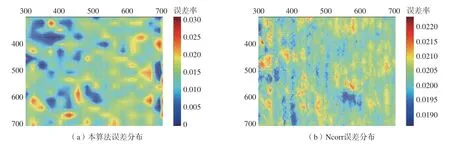
图9 误差分布Fig.9 Error distribution
可以看出,本算法分析误差不超过3%,Ncorr的分析误差不超过2.3%,结果表明,本算法具有良好的准确度。获得全场位移数据后,欲求某点应变,可采用最小二乘法将该点周围的位移数据拟合为一个平面,基于平面的斜率求解应变,即
式中,A为(用坐标数据构造的)系数矩阵;w为待求解向量;b为(用位移数据构造的)列向量。其中,(xi,yi)表示图片上的一个像素位置;zi表示该位置在x或y方向的位移ui或vi;n表示用于拟合这个平面的点的个数,当点的个数超过3时,w存在最小二乘解,其两个分量a、b分别是平面沿着x、y方向的斜率。将ui和vi分别作为zi代入,计算出au,bu与av,bv,则应变增量的分量为
最后基于平面应变假设获得等效应变增量为
3 试验结果
开展了两组剪切区应变率监测与调控试验,切削参数、应变率目标值和可接受应变率误差设定如表1所示, 图10展示了调控试验中获得的部分图片和相应的分析结果。
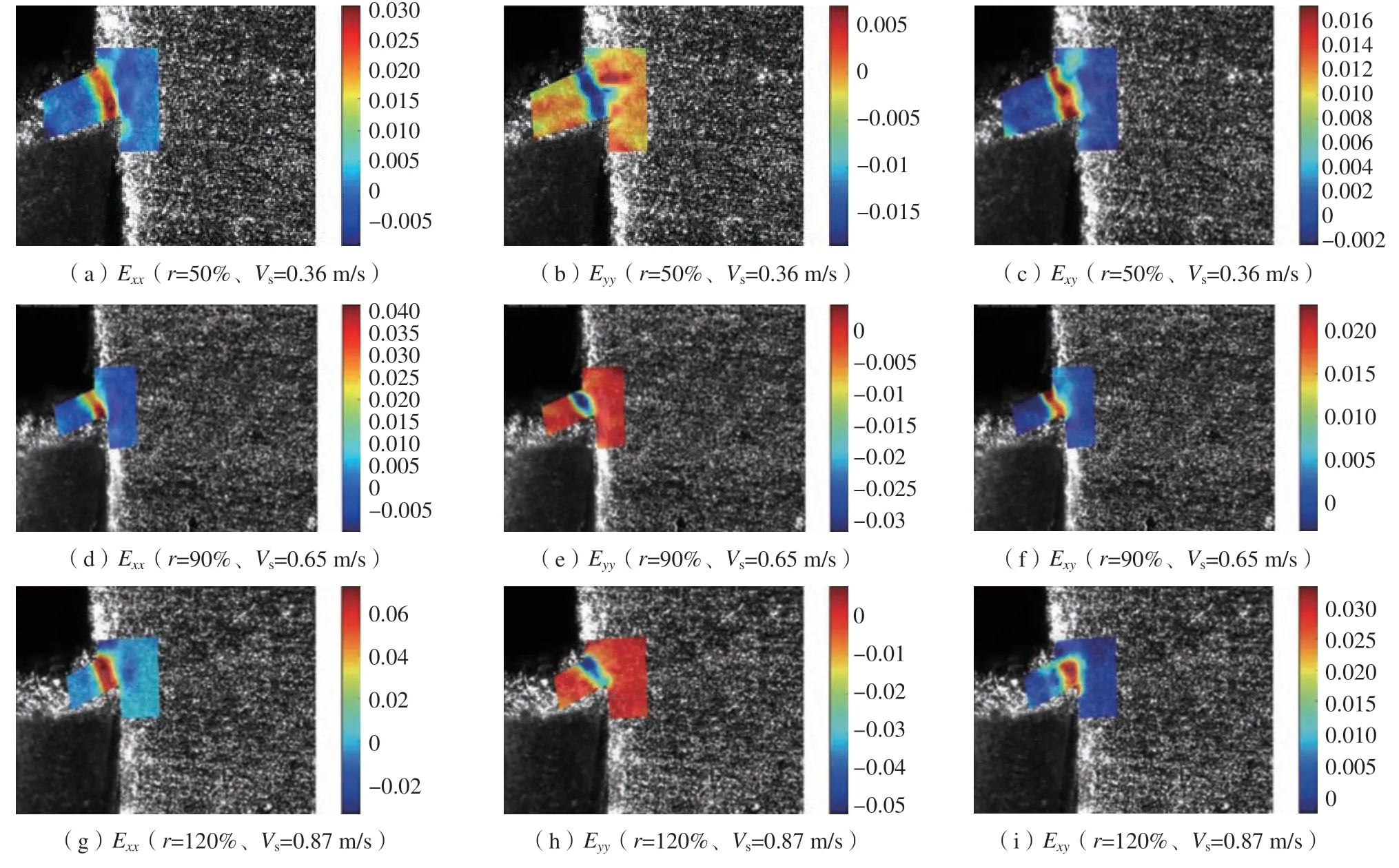
图10 不同主轴倍率下的剪切区应变增量Fig.10 Cutting shear zone strain increment under various principal axis rates

表1 试验参数设计Table 1 Experimental parameter design
试验过程实时测算的应变率和主轴倍率 (切削速度)如图11所示,纵坐标表示应变率大小,横坐标表示相机曝光次序。可以看出,当实际的应变率低于设定值,软件发送信号控制机床提高主轴倍率;当实际应变率高于设定值时,软件发送信号控制机床降低主轴倍率。主轴倍率的变化会使得应变率逐步接近设定目标值,最终实测应变率在目标区间以内,与目标值误差小于10%,符合预设要求。
此外,采用Lalwani等[23]提出的Oxley理论,应变率预测公式表征了应变率随速度的变化关系,剪切区应变率解析计算公式为
理论预测值与试验测量值对比如图11所示,随着主轴转速倍率的变化,两者基本吻合。在小应变率下,误差达到23%。在较大的应变率下,误差通常小于16%,表明了所构建的剪切区应变率监测和调控精度。
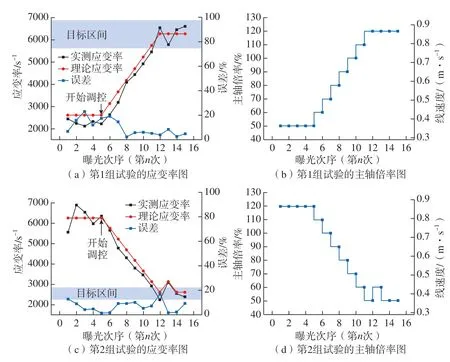
图11 实测、理论应变率图与主轴倍率图Fig.11 Measured, theoretical strain rate diagram and spindle magnification diagram
4 结论
(1)实现了由多线程加速的全局DIC算法,在5线程并行处理待分析区域 (6 ~ 8万像素点)时,计算过程需要的时间为1 ~ 2 s,计算位移误差小于3%。
(2)所提出的系统可以在正交切削过程中实时、准确地监测剪切区应变率大小,并与所设定的目标值对比,给出控制信号改变切削速度完成对应变率的调节,两组试验结果表明试验测量值与目标值偏差小于10%,而与Oxley理论预测模型相比,误差小于23%。
本文的工作为航空发动机零件加工表面完整性调控提供了一条新的技术途径,后续将进一步提高该系统的稳定性和适用性,并应用于复杂曲面典型加工工况下的加工表面完整性的在线调控。
