基于AIS数据的航运物流港口调度优化研究

白响恩，李博翰，徐笑锋，肖英杰

基于AIS数据的航运物流港口调度优化研究

白响恩，李博翰，徐笑锋，肖英杰

（上海海事大学 商船学院，上海 201306）

针对宁波舟山港区的复杂航道水域与密集物流交通流，研究更加有效的调度方案，达成调度时间和等待时间最小化，即效率最大化。分析宁波舟山港区航道的航行情况，提出交会处复杂航道水域存在的问题，以调度时间和等待时间最小为目标的多目标函数，建立复杂航道水域船舶调度模型。针对大量的船舶AIS数据，构建基于神经网络的航道水域调度模型，对不同类型、不同大小的船舶建立速度变化和船舶预测模型，实现对船舶调度状态的预测。设计以传统粒子群算法为基础的改良版船舶调度算法。算法对模型求解表明，根据不同船长与间距可判别交通流拥挤程度进而对船舶进行调度。通过模型预测到可能产生拥挤，则应当选择小型船只走条帚门航道，大型船只走虾峙门航道，并且尽量避免产生拥堵。使用该模型与算法可以有效地提升船舶调度效率，为复杂航运物流港口调度优化研究提供了一定理论基础。

复杂航道；深度神经网络；粒子群算法；船舶调度；AIS数据

航运物流业正向着拼箱货物的增加，应急、备用及时性货物的运输量增加以及数字化的方向发展。导致船舶大型化、智能化、低碳化的发展，对船舶调控的要求也越来越高。在港口作业、船舶运输方面，船舶调度在保障港口正常运行，船舶物流快速到达等起到重要的作用，通过港口信息调度中心，根据港口当前或未来一段时间的预测情况对所涉及的船舶进行交通指挥，以达到节约船舶在港口航行作业时间的目的[1]。2021年苏伊士运河事件导致船舶大规模滞留，造成的损失成本无法估量。这暴露出了在亟需高效作业、港口运河疏通时的调度问题。港口船舶占用通道时间长、船舶通行时交岔会遇等问题极大地影响了港口和运河地作业效率[2]。

天津港港区航道水域改建工程、长江口水域改造工程等[3]，通过预估未来船舶通行量需求以及船舶运行轨迹等对航道进行改造。在此基础上，根据港口的情况进行科学有效地调度，可以减少船舶出入港的时间，减少船舶碰撞的风险，做到安全性与经济效益兼顾[4]，但是由于各种因素导致船舶调度相关研究在现实应用中受限，很多港口依旧采用人工经验调度法，效果较为低下。所以，很有必要对船舶调度进行研究，同时主要根据港口和航道本身的情况对调度进行分类[5]。根据水域类型分为单向、双向和复杂航道水域，不同的类型对船舶调度的要求也不同，但是目的都是调度和等待时间最少[6]。

顺序调度模型可以有效地减少船舶的等待时间，但是这种算法用于船舶调度优化时[7]，每一轮的船舶通航顺序会对自己一轮甚至下一轮造成影响，在模型建立时应该提出船舶等待时间上限。船舶航行时与时间结合的预测模型，即RECIP–MILP模型是由Paola Pellegrini提出的[8]，该模型说明了当运河布局具有明确的结构时如何将距离安全约束转换为时间约束。

目前，单向航道和双向航道的调度问题研究已经取得了一定的研究成绩，但是复杂航道水域因其多变性和人为因素对其干扰影响大，难以以单一的模型或者算法将其概括。对于某种特定的复杂航道水域研究，常从水域交通流量统计与预测，水域通过能力，水域风险评估及安全因素等进行调度规划[9]，但这些研究，均存在单切入点的情况，无法做到从全局的角度考虑调度最优问题[10]。另一方面，随着技术的发展，信息技术以及人工智能等相关理论在航运届逐渐展开应用[11]，船舶调度逐渐向智能化、高效化作业形势转变[12]。结合当前的AIS技术等，对船舶港内航行，船舶出入港和港口进行管理调度[13]。

从单水域航道和双水域航道的经验出发，总结并设计复杂航道水域的模型与算法。调度相关算法中遗传算法使用最广，其优化方法也层出不穷[14]。本质上就是改进了随机产生的过程，使仿真模拟收敛更快[15]。将弹性网络概念加入遗传算法，在低密度水域网格上可以提高调度规划效率[16]。在选取随机算子时，可以使用轮盘赌进行选择。轮盘赌随机选择一个变异点，进行变异操作得到新的个体[17]，这样可以降低出现过早收敛的概率。设立惩罚函数，在未满足约束时需要受到惩罚。再采用精英策略，让适应度高的个体直接进入下一代，再用轮盘赌的方式对剩余群体进行选择，这样可以有效防止优良解的丢失[18]。退火算法的原理是固体经过增温和降温，内部粒子从有序变为无序再变成有序，在常温时固体内能最小[19-20]。粒子是算法的解，内能是解的目标值[21]。多种群遗传算法的加入，改善遗传算法的局部最优和收敛过慢问题[22]。降温后的搜索范围迅速缩小可以使收敛速度提高[23]。蚁群算法可以划分静态权值和动态权值来衡量航线权重，静态权值是用船舶航行距离衡量，动态权值是用经济效益[24]衡量。改进蚁群算法优先选择行走实时方向角与初始方向角相同的路线，至下一节点，重新选择路线直到终点，减少了从零开始迭代的迭代次数[25]。

调度相关的算法还包括粒子群优化算法、Dijkstra算法、A*算法、细菌觅食神经网络算法[26]。同时还有将2种算法结合，如粒子群优化算法和多物种遗传算法进行结合，可以加快粒子群优化算法的运算速度和优化精确程度[27]。Dijkstra算法可以在遗传算法的基础上进行改造。A*算法在静态网络中通过对A*函数进行优化，添加相应的约束条件以及修正估价函数可以加快A*函数运算速度[28-29]。神经网络算法主要用于构造环境变量[30]。

随着宁波舟山港的发展建设，在保证安全与遵守航行规则的前提下，提高港口运行效率，保障航线安全是港口运营的核心问题[31]。目前存在高峰时期通过能力不足，小型船只占用航道时间过长等[32]。文中从宁波舟山港区的复杂航道水域优化开始，探究复杂航道水域的优化模型和算法。

1 航道分析

1.1 条帚门航道与虾峙门航道分析

条帚门航道整体的特点就是航道窄、水深、流急，可以满足30万t级的船舶通过，但是由于航道宽度狭窄、水深不富余等，航道宽度最窄的地方只有500 m，这种条件使得船舶效应和岸壁效应更加明显，渔船众多使航道的情况更加复杂。

因为虾峙门航道北口处存在一号警戒区，这个位置是通航分道进入口，而且船舶众多，事故频发，所以可以将船舶出港路线选择为条帚门航道，这样可以减少一号警戒区的压力；小型船舶的进港路线尽量选择条帚门航道，10万t级以上的船舶进出港尽量选择虾峙门航道，如果存在航行能见度低、虾峙门航道拥挤时，可以考虑选择条帚门航道，但是要时刻注意几个浅水区域。

1.2 y型航道交岔口问题描述

1.2.1 交汇口地理情况

图1为虾峙门航道和条帚门航道y型交岔口的整体框架，具体包括出入港区的主航道和从虾峙门航道和条帚门航道出入的双向航道以及警戒区。警戒区位于在虾峙门航道和条帚门航道航道交汇处。交岔口以及主航道处的水域较为宽阔，水深满足能通过虾峙门航道和条帚门航道的船舶的吃水要求。

1.2.2 交岔交通流分析

进出港口和通过虾峙门航道和条帚门航道的船舶都必须经过交岔口，如图1所示，y型交岔口主要受到以下2股交通流冲突的影响：第1股交通流冲突为条帚门航道进港船流与虾峙门航道进港船流交岔；第2股交通流冲突为条帚门航道进港船流与虾峙门航道出港船流交岔。

图1 交通流交汇分析

1.2.3 警戒区分析

由图2所示，警戒区处有3个冲突点已在途中标明。在船舶的交汇航行过程中，对这3个冲突点可能存在的交通事故进行预测，一方面可以提高航行的安全性，另一方面，预防交通事故的发生也间接地提高了港口调度的效率。

按照警戒区的交通冲突严重性进行划分，采用空间距离法、时间距离法或者是碰撞危险度参数法可以将交通冲突划分为3个等级：一般冲突、中等冲突和严重冲突。按照一定的评价标准可以建立对警示区安全等级评价的评价指标，针对不同的安全影响因素赋予一定的安全评价权重，最后将安全评价权重累积起来得到警戒区的安全等级评价。期望法模型、熵权法模型或者超熵法模型通过仿真实验进一步对警示区进行评级。

1.3 待解决关键问题

传播在航行调度过程中，由于影响因素和不可抗力因素过多，需在模型设立过程中做好取舍。首先需要考虑船舶大小、类型等；其次水流速度、天气情况也是可能造成影响的因素；还有人为因素也会对船舶调度过程产生影响。此外，船舶需要严格地遵循调度过程中预设的航行规则，以确保航行的安全性。

如果仅单纯地使用宁波舟山港区VTS技术，无法准确地提供调度策略。通过大数据将以往的AIS数据进行处理分析，结合未来一段时间AIS数据的预测，利用大数据的特点，在相对理想的状态下完成对船舶调度的过程模拟。针对出现特殊情况的数据进行分析与处理，最终得到更有说服力的实例应用，并在发生一系列轻微影响的突发情况时可以随时添加影响因素变量，使得模型更加准确。

船舶调度的最终目的是时间成本的最低化与经济效益的最大化，但是航行中最为重要的一点一直是安全性。在充分分析船舶交会情况与警戒区情况的前提下，对船舶调度整个过程坚持安全优先，进一步结合VTS技术和AIS数据对船舶进行调控。

2 模型的设计与建立

2.1 船舶分类

按照船舶的大小和类型以及进出港情况给每艘报备进出港的船只赋予一定的权重，由于条帚门航道进出的船舶多为小于10万t级，可以粗略地按照10万t为界限进行划分，则对10万t级以上的船只给予更高的船舶权重系数，同时出港船只权重系数也更高。具体来说，一般进港船只系数为1.00，10万t以下出港船只和10万t以上进港船只系数为1.25，10万t出港船系数只取1.50。将权重系数分别乘上船舶的航行时间和等待时间即为该艘船舶的目标值。

2.2 模型约束条件

根据航道通航规则建立4个模型约束。

1）船舶之间安全距离约束，船长200 m以上的船舶应与前船保持1 n mile以上的距离。超大型油轮应与前船保持1.5 n mile以上距离，由安全距离和船舶航速计算出最短船舶航行间隔，作为约束条件1。

2）根据第1种交岔口交汇情况，设置安全距离，保持船舶距离大于安全距离，由安全距离和船舶航速计算出最短船舶航行间隔，作为约束条件2。

3）根据第2种交岔口交汇情况，设置安全距离，保持船舶距离大于安全距离，由安全距离和船舶航速计算出最短船舶航行间隔，作为约束条件3。

4）如果采用的是等待时间限制方案，则将等待时间上限作为约束条件4。

2.3 建立模型函数

在对港区航道环境分析的基础上，确定以调度时间和等待时间最短为目标，建立复杂航道水域调度模型。

在保证约束的情况下使模型的目标函数1和2最小即可。

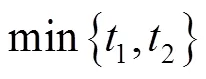
目标函数1：总的调度时间1最小。

(2)

式中：fi为船舶调度结束时刻；si为船舶调度开始时刻。

目标函数2：总的船舶等待时间2最小。

船舶在来到交岔口的时候，即开始计算等待时间，总的船舶等待时间更小，即代表港口运行的效率更高。

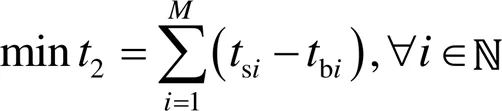
式中：bi为船舶到达交岔口的时间。

根据对约束条件的分析，通过对船舶进出港的不同情况和船舶大小的不同情况设置船舶优先权重，将船舶大小和船舶进出港的影响因素权重考虑进模型内。

再根据船舶的不同类型权重m，以及船舶的特殊类型权重r计算船舶通航的具体权重：

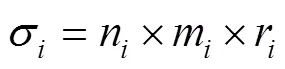
对于越需要紧急通航的船舶将r设置的更大即可，根据σ的不同对船舶通航等级排序，得到最初的船舶通航顺序。

通过统计船舶进入和驶离交岔口、进入或者离开航道的时刻可以得到船舶的航行结束时刻的预估值，见式（6）。

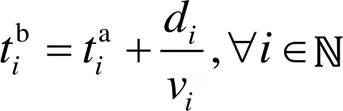
式中：d为、两处的距离。

进一步考虑约束条件1，根据船舶之间的间距和船速估计船舶之间通航的安全间隔时间，见式（7）。

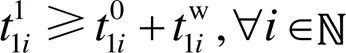
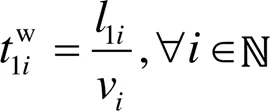
考虑约束条件2，约束条件2为船舶之间同向进入交岔口的交通流交汇情况。当出现从虾峙门航道和条帚门航道均有船舶需要进入港区的情况时，两船之间也需要保持一定的船舶安全航行间隔：

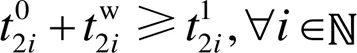
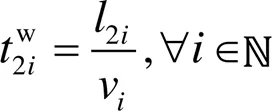
与约束条件1同理，2i0和2i1分别为先后进入主航道的船舶的航行开始时刻；为两船之间的航行安全时间间隔；2i为设置好的船舶之间的安全距离。

约束条件3为船舶之间异向进入交岔口的交通流交汇情况：

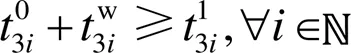
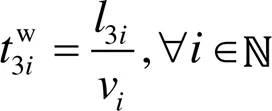
约束条件4为设置船舶最大等待时间pi：

则计算船舶开始到达交岔口时间与开始航离时间的差值即可。

3 算法设计

以宁波舟山港区虾峙门航道和条帚门航道的航道情况为基础，从交通流交汇的角度，以及符合交通安全，遵守航行规则的角度出发，结合航道一段时间内的AIS数据，提出一种以深度学习神经网络为基础的船舶航行状态预测模型。同时，使用改进的粒子群算法对模型进行优化，使模型更贴合实际情况，通过分析船舶在出港时的船速与调度间隔时间，给出使拥堵情况可能性降到最低的船舶调度办法。以Matlab软件为程序编写平台对该模型进行验证。

3.1 AIS数据预处理

特定时刻的船舶AIS数据中动态的数据包括船舶瞬时的对地航向、对地航速等，同时也会有静态数据，如船舶的长度、吃水、宽度等。AIS数据不仅包含了船舶不同的航行状况，也蕴含了船舶在港口因为船舶间作用影响的状况。对一段时间内的大量的AIS数据进行分析，可以利用大数据与深度学习模型对在港其他船舶的航行信息进行预测[33]。

表1是部分AIS数据的原始样本数据，对原始的AIS数据记录往往存在大量的噪声以及错误数据，为此需要对AIS数据进行一定标准的预处理，需要进行处理的数据包括船舶位置异常，船舶航向、航速异常，船舶基础长度、宽度、吃水数据异常。

记单个AIS数据样本为p=(t,x,y,c,h,l,w,d),(=1,2,3,…)，其中t为AIS数据采样时间，x和y分别代表经度和纬度，c, h,l,w,d分别代表船舶对应的对地航向、船首向船长、船宽和吃水深度。将样本数据输入Matlab中，编写删除异常数据样本的脚本，其中设定船舶和合理范围为[0, 360]，设定船舶长宽和吃水应为大于0的数。将虾峙门航道和条帚门的AIS数据样本分别带入得到预处理后的数据样本，流程见图3。

3.2 神经网络的运用

深度学习与大数据结合，减少了在对研究检测对象进行预测时产生的误差。在航运领域应用深度学习进行数据处理分析现阶段还较少。文中考虑将预处理之后的AIS数据与深度神经网络进行结合，建立船舶动态预测模型。深度学习的权重随着迭代的进行，可进行粗略的求解，文中引用G. E. Hinton的论文结论，见式（14）。

式中：为学习率；为代价函数。

图4为文中使用的深度神经网络的示意图，其中输入圆圈代表船舶信息，输出圆圈代表需要进行预测的信息。运用贝叶斯神经网络模型，通过调整神经元个数以及训练集、测试集的数量将深度学习神经网络模型的误差尽可能降低。

3.3 遗传算法

只使用模型带入数据进行求解得到的结果往往不具有随机性代表性，为此利用遗传算法对模型进行优化。

设定船舶编号、进出港方向、船舶类型以及航行起点终点位置的4位遗传算子，以表示船舶的基础数据。如：1101代表1号船舶从港口出来，为大型的集装箱船，经过主航道向虾峙门航道航行。

在算法中要考虑适应度函数的取值。适应度越大，被选择的概率就越大，本模型目标函数是总调度时间和总等待时间最小，如果调度时间越小，等待时间越短，说明个体的适应度越大，因此用等待时间的倒数作为适应度函数值，见式（15）。在实际过程中由于船舶等待时间存在上限，故可以设定一个上限值。如果船舶的等待时间已经达到了上限值，也要降低该个体的适应度值，以此让优秀的个体更好地遗传下去。

其他相关的算法中采用轮盘赌的方式选择算子，交岔算子采用两点交岔的方式，变异算子采用两点变异的方式，具体过程见图5。

表1 原始AIS数据

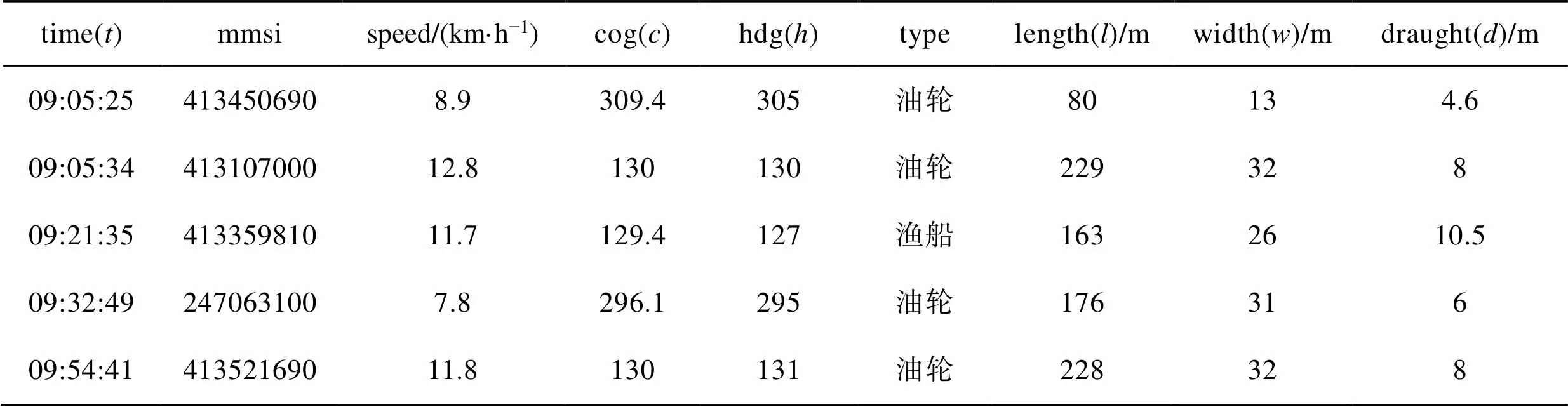
Tab.1 Original AIS data

注：time为时间，mmsi为水上移动通信业务标识码，speed为航速，cog为对地航向，hdg为船首向，type为AIS船舶类型，length为船长，width为船宽，draught为吃水。

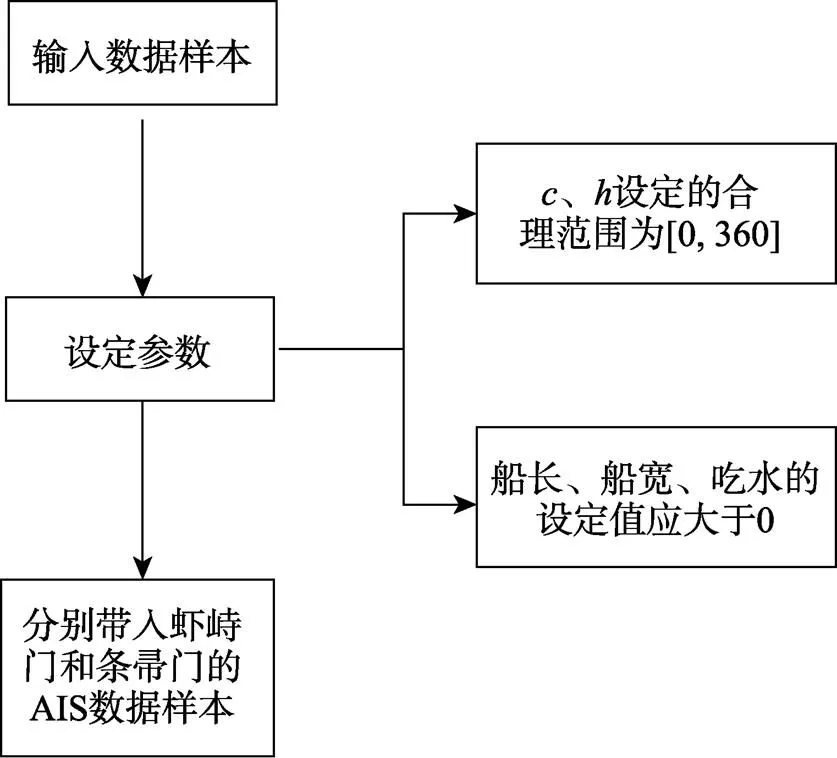
图3 利用Matlab处理AIS数据流程

图4 船舶调度深度神经网络

3.4 利用改进粒子群算法对预测信息进行优化

粒子群优化算法将每个样本看作维空间中的忽略体积的粒子X=(x1,x2, …,x)，分别计算样本初始的个体值，得到最好的个体值（最好的位置）记为pbest，即P=(p1,p2, …,p)，给粒子群赋予速度V=(v1,v2, …,v)，每次迭代后再计算粒子对应的个体值，将群体中的最优个体值（最好的位置）记为gbest，即G=(g1,g2, …,g)。对于每次的迭代，一般每一维的速度都有上下限的设定，个体值也可以设定上下限。

传统的粒子群算法多用于对多维样本进行寻优，文中利用粒子群算法的特性，结合前文已建立的深度学习神经网络模型，将模型得到的预测结果进行优化。其中，对船舶本身而言，船舶长度、宽度和吃水是不发生变化的，故仅将船舶速度、所在的经纬度、对地航向、船首向作为考虑因素。传统的粒子群算法是现在每代中得到群体最优粒子，再从这些群体最优粒子中选择总的最优粒子。在程序的编写中，传统的粒子群算法是对群体进行迭代，更新速度采用最优粒子与样本个体值做差再随机化。文中采用的改进方法是对每个样本点（即每艘船舶的样本值）单独进行迭代，最终结果也相互独立，而不是取群体最优值。

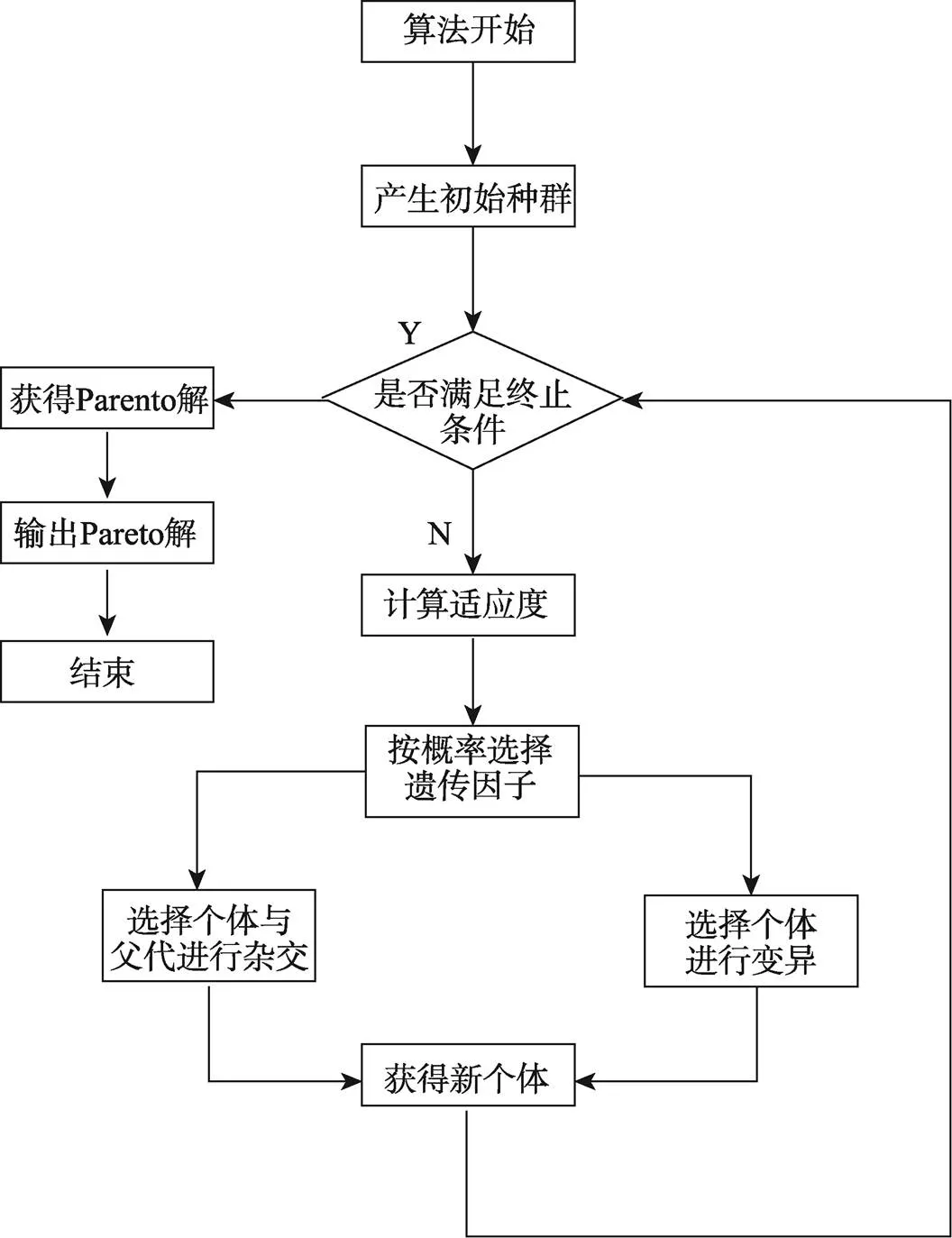
图5 算法流程

设计的粒子群算法基础参数及流程见图6a。maxgen为粒子群进化次数上限，sizepop为粒子群种群规模，Vmax和Vmin分别为粒子群迭代速度的最大值和最小值，popmax和popmin分别为粒子群基础参数最大值和最小值，pop为样本值。

在准备迭代时，需要先产生新迭代的迭代速度，在产生后进行迭代得到下一代粒子群，将粒子反代回求解出适应度，并通过比较的方法得到最佳的粒子适应度，记下该粒子数据，具体流程见图6b。fitness为样本适应度，fun为深度学习神经网络模型函数，zbest和gbest分别代表全局最佳粒子和个体最佳粒子，fitnessgbest代表个体最佳粒子对应的适应度。

产生新一代粒子群，通过一一比较确定最佳粒子以及其适应度，将该粒子及其最佳适应度记录，作为暂时最佳适应度，具体的改进粒子群算法流程见图6c。

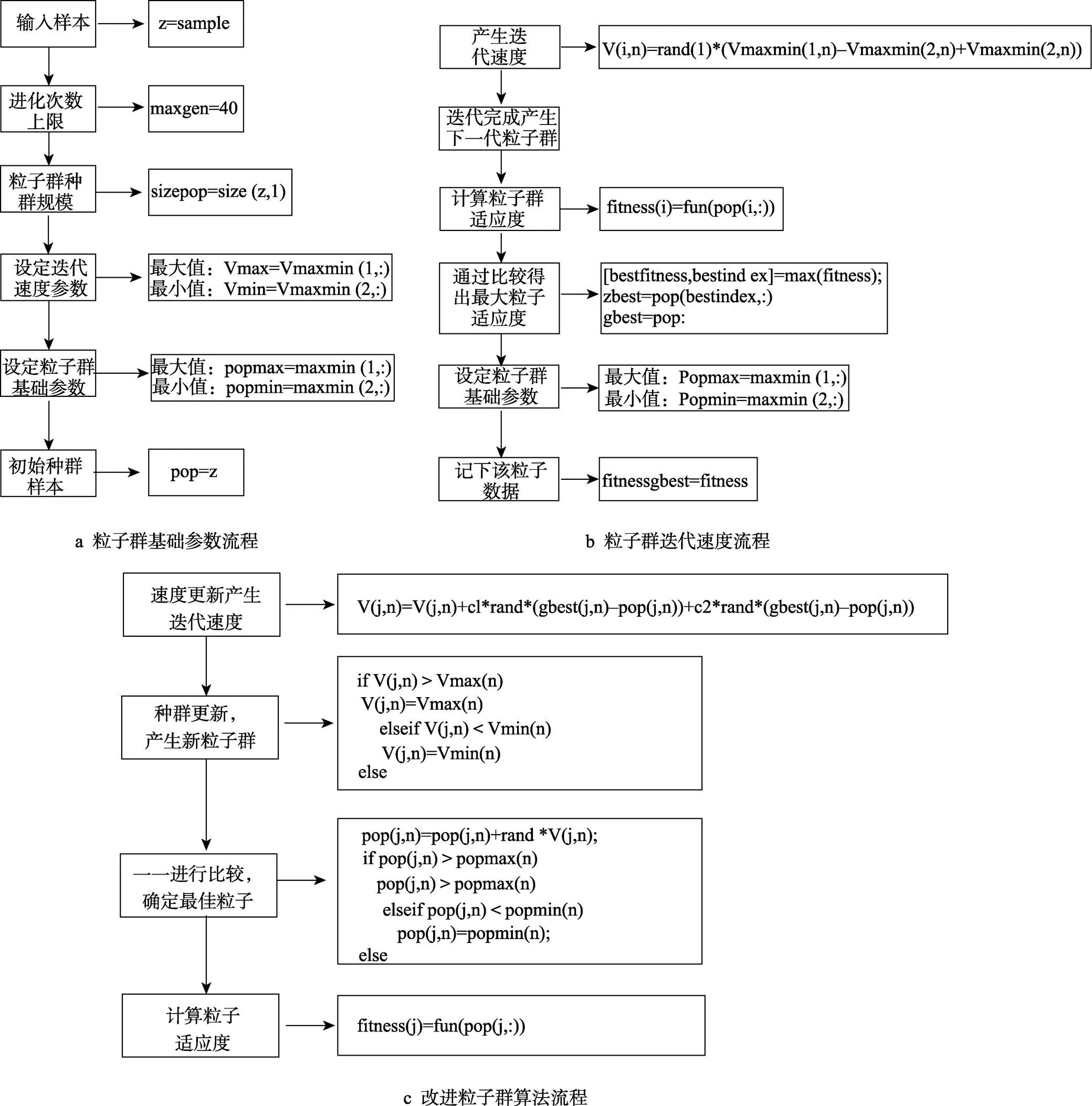
图6 粒子群算法相关流程及伪代码

4 宁波舟山港区实例应用

前文分析得出一般情况下，在避免拥堵的范围内大部分的船舶从核心港区出港选择虾峙门航道更加合理，一旦通过模型预测到可能发生拥挤，则应当选择小型船只走条帚门航道，大型船只走虾峙门航道，并且尽量避免拥堵的产生。

根据现行港口管理条例，船舶之间安全距离约束，船长200 m以上的船舶应与前船保持1 n mile以上的距离。超大型油轮应与前船保持1.5 n mile以上距离，由安全距离和船舶航速计算出最短船舶航行间隔。

在此案例中将上文粒子群算法中的适应度函数设定为船舶可能达到的最大平均航速，由于已知数据包括船舶出入港时间间隔，如果最大预测船速都无法满足调度需求，即大概率会发生拥堵情况，可以得到船舶在调度时间间隔内按照预测优化后的航行状态进行航行，观察是否会产生拥堵状态，以此为依据选择出港船舶的调度方式。

表2是宁波舟山港区一段连续时间内出港船舶的AIS数据，数据已经过预处理，符合模型的要求。对应的调度间隔时间见图7。从图7中可以看出，第2与第3艘次船舶、第7与第8艘次船舶、第11与第12艘次船舶较为拥挤，时间较短，应进行调度分流。

将AIS数据带入模型和算法中得到预测的船舶速度见图8。

表2 样本数据AIS

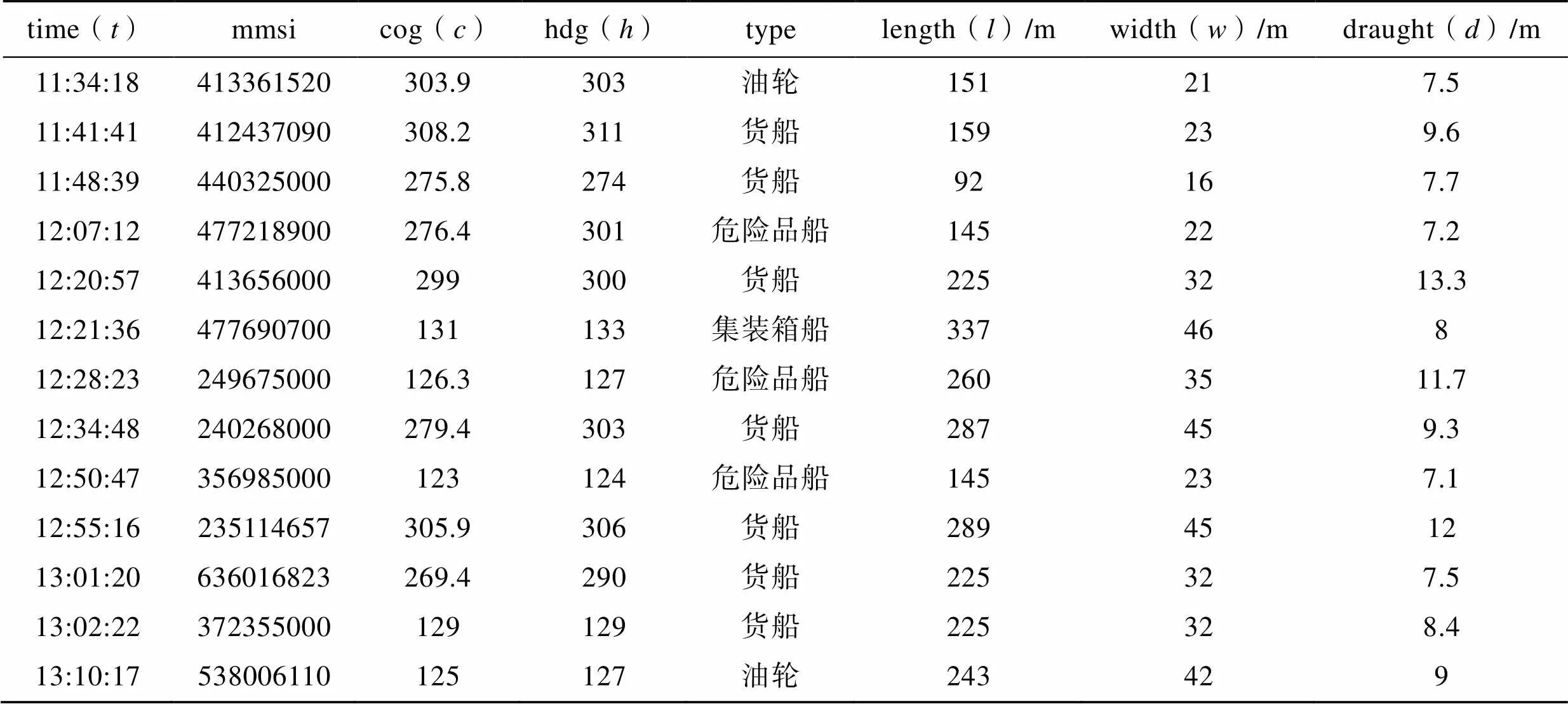
Tab.2 AIS of sample data

注：time为时间，mmsi为水上移动通信业务标识码，cog为对地航向，hdg为船首向，type为AIS船舶类型，length为船长，width为船宽，draught为吃水。

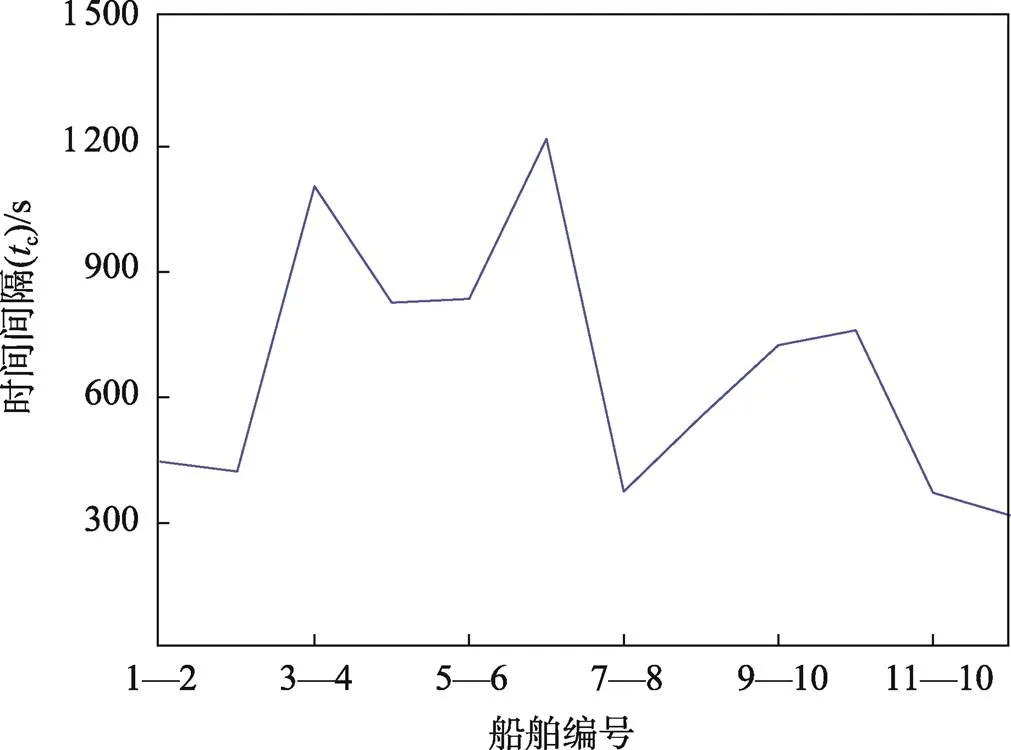
图7 船舶调度时间间隔

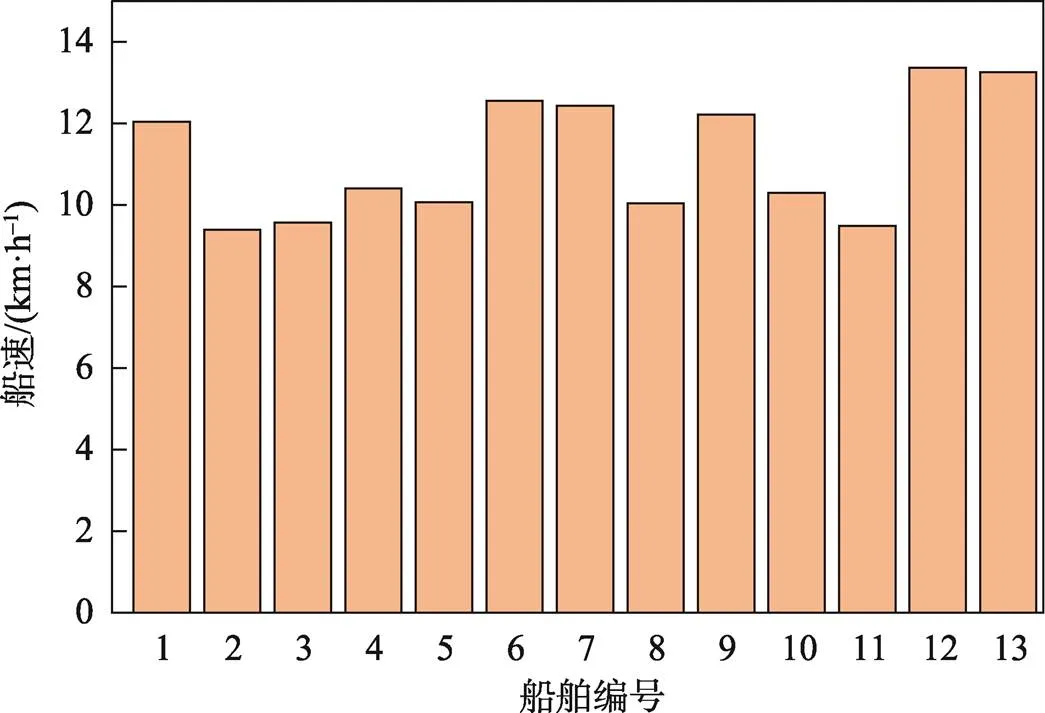
图8 船舶预测船速

根据表2中内容求得实际调度中预测的间距：

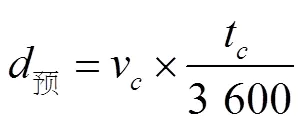
式中：预为预测间距；c为预测最大平均船速；c为船舶调度时间间隔。得到间距见图9。

如果按照1 n mile间距的船舶安全距离来看，选择第12艘次船舶从条帚门航道出港，第11艘次船舶和第13艘次船舶从虾峙门航道出港，其他船舶的选择对拥堵状况影响不大，按照小型船只尽量走条帚门航道的标准，可以将第3艘船只从条帚门航道出港。

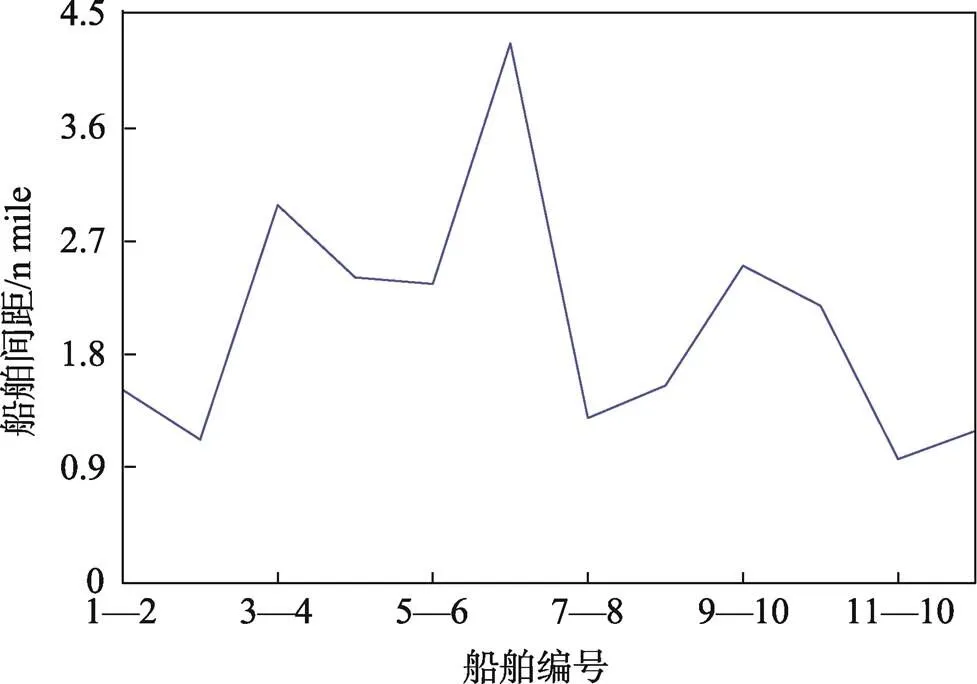
图9 船舶距离

模型的提出和算法的求解，目的是为了提高港口生产效率，充分利用航道。虽然通过智能算法提出智能调度方案，但是依然利用AIS和VTS通过频道对讲人工进行调度，通过引航员工作，带领船舶进港。目前只有虾峙门航道发生了拥堵，条帚门航道才作为应急航道，只有在虾峙门航道禁航的情况下才会进行分流走条帚门航道。

5 结语

在以往的调度经验中大部分的船只都只从虾峙门航道通行，条帚门航道则由于地理因素等一系列的原因使用较少。利用AIS信息，结合大数据与深度学习神经网络算法建立航行预测模型，同时使用改进粒子群优化算法对模型进行优化，结合对宁波舟山港区虾峙门航道和条帚门航道不同的地理环境的分析建立优化调度模型，最后利用虾峙门航道和条帚门航道的AIS数据样本抽样对模型和算法进行验证，得到船舶出港调度顺序的结果。实例证明第2与第3艘次船舶、第7与第8艘次船舶、第11与第12艘次船舶较为拥挤，安全距离考虑第12艘次船舶走条帚门进港较为合理。该模型与算法可优化港口航运调度，为港口发展和提高物流效率具有一定理论指导意义。

[1] 王金涛. 基于单向航道的船舶调度优化模型与算法研究[D]. 大连: 大连海事大学, 2014: 8-75.

WANG Jin-tao. Research on Vessels Scheduling Model and Algorithm Based on One-Way Channel[D]. Dalian: Dalian Maritime University, 2014: 8-75.

[2] 徐海栋. 港口海侧交通组织优化研究[D]. 大连: 大连海事大学, 2018: 8-66.

XU Hai-dong. Research on Optimization of Port Seaside Traffic Organization[D]. Dalian: Dalian Maritime University, 2018: 8-66.

[3] 张新宇, 李瑞杰, 张加伟, 等. 多种航道条件下的港口船舶交通组织优化[C]// 第十三届中国智能交通年会大会论文集, 中国智能交通协会, 2018: 708-717.

ZHANG Xin-yu, LI Rui-jie, ZHANG Jia-wei, WANG Zhi-qiang. Optimization of Port Vessel Traffic Organization Under Multiple Channel Conditions[C]// Proceedings of the 13th China Intelligent Transportation Annual Conference, China Intelligent Transportation Association, 2018: 708-717.

[4] 完剑侠, 缪克银, 张树奎. Y型航道内船舶交通流量的非线性特征研究[J]. 广州航海学院学报, 2019, 27(4): 8-12.

WAN Jian-xia, MIAO Ke-yin, ZHANG Shu-kui. Research on Nonlinear Characteristics of Ship Flow in Y-Type Waterway[J]. Journal of Guangzhou Maritime Institute, 2019, 27(4): 8-12.

[5] 张新宇, 李瑞杰, 林俊, 等. Y形分叉复式航道船舶交通调度优化建模[J]. 大连海事大学学报, 2018, 44(2): 1-8.

ZHANG Xin-yu, LI Rui-jie, LIN Jun, et al. Optimization Modeling of Vessel Traffic Scheduling for Y Shaped Bifurcated Compound Waterway[J]. Journal of Dalian Maritime University, 2018, 44(2): 1-8.

[6] 陈向. 复式航道条件下的港口船舶调度优化[D]. 大连: 大连海事大学, 2017: 9-61.

CHEN Xiang. Optimization of Port Ship Scheduling under the Condition of Compound Channel[D]. Dalian: Dalian Maritime University, 2017: 9-61.

[7] 文元桥, 郑海涛, 周春辉, 等. 基于复杂性地图的多船避碰模拟[J]. 武汉理工大学学报(交通科学与工程版), 2017, 41(3): 401-405.

WEN Yuan-qiao, ZHENG Hai-tao, ZHOU Chun-hui, et al. Simulation of Multi-Ship Collision Avoidance with the Complexity Map[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2017, 41(3): 401-405.

[8] 余文曌, 佘航宇, 欧阳子路. 基于弹性网格的改进遗传算法在无人艇路径规划中的研究[J]. 中国航海, 2018, 41(4): 101-105.

YU Wen-zhao, SHE Hang-yu, OUYANG Zi-lu. Path Planning of Unmanned Surface Vehicle Based on Variable Mesh Improved Genetic Algorithm[J]. Navigation of China, 2018, 41(4): 101-105.

[9] 张春玮, 马杰, 牛元淼, 等. 基于行为特征相似度的船舶轨迹聚类方法[J]. 武汉理工大学学报(交通科学与工程版), 2019, 43(3): 517-521.

ZHANG Chun-wei, MA Jie, NIU Yuan-miao, et al. Clustering Method of Ship Trajectory Based on Similarity of Behavior Pattern[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2019, 43(3): 517-521.

[10] 刘娇, 史国友, 杨学钱, 等. 基于DE–SVM的船舶航迹预测模型[J]. 上海海事大学学报, 2020, 41(1): 34-39.

LIU Jiao, SHI Guo-you, YANG Xue-qian, et al. Ship Trajectory Prediction Model Based on DE-SVM[J]. Journal of Shanghai Maritime University, 2020, 41(1): 34-39.

[11] 方琼林, 邵哲平, 潘家财, 等. 天津港大沽沙航道交通组织优化[J]. 集美大学学报(自然科学版), 2015, 20(5): 365-370.

FANG Qiong-lin, SHAO Zhe-ping, PAN Jia-cai, et al. Study on the Optimization of Traffic Coordination in Tianjin Dagusha Waterway[J]. Journal of Jimei University (Natural Science), 2015, 20(5): 365-370.

[12] 甘浩亮. 港口水域LNG船舶交通组织优化研究[D]. 武汉: 武汉理工大学, 2012: 7-72.

GAN Hao-liang. The Study on Traffic Organization and Optimization of LNG Vessel in Port Waters[D]. Wuhan: Wuhan University of Technology, 2012: 7-72.

[13] 周伟, 肖英杰, 吴善刚, 等. 基于Anylogic的耙吸装驳作业船舶交通组织仿真[J]. 中国航海, 2019, 42(2): 42-46.

ZHOU Wei, XIAO Ying-jie, WU Shan-gang, et al. Simulation on Vessel Traffic Organization for TSHD Loading Barge Operation Using Anylogic Software[J]. Navigation of China, 2019, 42(2): 42-46.

[14] 倪生科, 刘正江, 蔡垚, 等. 基于混合遗传算法的船舶避碰路径规划[J]. 上海海事大学学报, 2019, 40(1): 21-26.

NI Sheng-ke, LIU Zheng-jiang, CAI Yao, et al. Ship Collision Avoidance Path Planning Based on Hybrid Genetic Algorithm[J]. Journal of Shanghai Maritime University, 2019, 40(1): 21-26.

[15] 陈成明, 虞丽娟, 李加林, 等. 基于改进遗传算法的远洋渔船船队调度路径优化[J]. 上海海事大学学报, 2016, 37(4): 1-6.

CHEN Cheng-ming, YU Li-juan, LI Jia-lin, et al. Scheduling Route Optimization of Ocean Fishing Fleet Based on Improved Genetic Algorithm[J]. Journal of Shanghai Maritime University, 2016, 37(4): 1-6.

[16] 陈超, 耿沛文, 张新慈. 基于改进人工势场法的水面无人艇路径规划研究[J]. 船舶工程, 2015(9): 72-75.

CHEN Chao, GENG Pei-wen, ZHANG Xin-ci. Path Planning Research on Unmanned Surface Vessel Based on Improved Potential Field[J]. Ship Engineering, 2015(9): 72-75.

[17] 霍凤财, 任伟建, 刘东辉. 基于改进的人工势场法的路径规划方法研究[J]. 自动化技术与应用, 2016, 35(3): 63-67.

HUO Feng-cai, REN Wei-jian, LIU Dong-hui. Research on Path Planning Method Based on Improved Artificial Potential Field Method[J]. Techniques of Automation and Applications, 2016, 35(3): 63-67.

[18] 范云生, 柳健, 王国峰, 等. 基于异源信息融合的无人水面艇动态路径规划[J]. 大连海事大学学报, 2018, 44(1): 9-16.

FAN Yun-sheng, LIU Jian, WANG Guo-feng, et al. Dynamic Path Planning for Unmanned Surface Vehicle Based on Heterologous Information Fusion[J]. Journal of Dalian Maritime University, 2018, 44(1): 9-16.

[19] 童帮裕, 胡坚堃. 基于改进蚁群算法的船舶冰区航行路径规划[J]. 中国航海, 2020, 43(1): 24-28.

TONG Bang-yu, HU Jian-kun. Improved Ant Colony Optimization for Navigation Path Planning in Ice Zone[J]. Navigation of China, 2020, 43(1): 24-28.

[20] 范云生, 赵永生, 石林龙, 等. 基于电子海图栅格化的无人水面艇全局路径规划[J]. 中国航海, 2017, 40(1): 47-52.

FAN Yun-sheng, ZHAO Yong-sheng, SHI Lin-long, et al. Global Path Planning for Unmanned Surface Vehicle Based on Grid Model of Electronic Chart[J]. Navigation of China, 2017, 40(1): 47-52.

[21] 罗贤程, 尹建川, 李宏宾. 基于动态分阶势场法的船舶自动避碰系统[J]. 上海海事大学学报, 2020, 41(1): 1-7.

LUO Xian-cheng, YIN Jian-chuan, LI Hong-bin. An Automatic Collision Avoidance System of Ships Based on Dynamic Hierarchical Potential Field Method[J]. Journal of Shanghai Maritime University, 2020, 41(1): 1-7.

[22] 陈立家, 黄立文, 崔梅. 基于改进蚁群算法的船舶多约束最优航线设计[J]. 上海海事大学学报, 2017, 38(4): 11-15.

CHEN Li-jia, HUANG Li-wen, CUI Mei. Optimal Ship Route Planning with Multiple Constraints Based on Improved Ant Colony Algorithm[J]. Journal of Shanghai Maritime University, 2017, 38(4): 11-15.

[23] 尚明栋, 朱志宇, 周涛. 基于改进蚁群算法的水面无人艇智能避碰方法研究[J]. 船舶工程, 2016, 38(9): 6-9.

SHANG Ming-dong, ZHU Zhi-yu, ZHOU Tao. Research on Intelligent Anti-Collision Method of USV Based on Improved Ant Colony Algorithm[J]. Ship Engineering, 2016, 38(9): 6-9.

[24] 陈卓, 茅云生, 宋利飞, 等. 基于进化势场模型的无人艇路径规划算法[J]. 武汉理工大学学报(交通科学与工程版), 2019, 43(1): 113-117.

CHEN Zhuo, MAO Yun-sheng, SONG Li-fei, et al. Path Planning Algorithm of USV Based on Evolutionary Potential Field Model[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2019, 43(1): 113-117.

[25] 薛翔, 朱小林. 基于优先权重粒子群算法的危险品运输路径优化建模[J]. 大连海事大学学报, 2016, 42(4): 112-118.

XUE Xiang, ZHU Xiao-lin. Modeling Hazardous Materials Transportation Routing Optimization Based on Prioritiesparticle Swarm Optimization[J]. Journal of Dalian Maritime University, 2016, 42(4): 112-118.

[26] 曾小龙, 茅云生, 宋利飞, 等. 基于改进细菌觅食优化的无人艇自主避碰算法[J]. 大连海事大学学报, 2018, 44(4): 35-42.

ZENG Xiao-long, MAO Yun-sheng, SONG Li-fei, et al. Automatic Collision Avoidance Algorithm for Unmanned Surface Vehicle Based on Improved Bacterial Foraging Optimization[J]. Journal of Dalian Maritime University, 2018, 44(4): 35-42.

[27] ZHU Da-qi, TIAN Chen, SUN Bing, et al. Complete Coverage Path Planning of Autono mous Underwater Vehicle Based on GBNN Algorithm[J]. Springer Netherlands, 2019, 94(1).

[28] 胡佳颖, 刘克中, 吴晓烈, 等. 基于前景理论的船舶避碰决策优化方法[J]. 中国航海, 2020, 43(1): 18-23.

HU Jia-ying, LIU Ke-zhong, WU Xiao-lie, et al. Optimization of Ship Collision Avoidance Decision-Making Based on Prospect Theory[J]. Navigation of China, 2020, 43(1): 18-23.

[29] 何傲, 谢新连, 李猛. 考虑安全性的施工水域路径优化[J]. 大连海事大学学报, 2019, 45(3): 114-120.

HE Ao, XIE Xin-lian, LI Meng. Route Optimization in Construction Waters Considering Safety[J]. Journal of Dalian Maritime University, 2019, 45(3): 114-120.

[30] 潘明阳, 刘乙赛, 李琦, 等. 基于改进A*算法的内河水网航线规划及应用[J]. 上海海事大学学报, 2020, 41(1): 40-45.

PAN Ming-yang, LIU Yi-sai, LI Qi, et al. Improved A* Algorithm Based Route Planning and Its Application for Inland Waterway Network[J]. Journal of Shanghai Maritime University, 2020, 41(1): 40-45.

[31] 闫化然, 薛松辉, 熊华, 等. 大型船舶进出洋山港四期码头交通组织[J]. 中国航海, 2018, 41(4): 53-56.

YAN Hua-ran, XUE Song-hui, XIONG Hua, et al. Traffic Organization of Large Vessels Entering Yangshan Port Phase Ⅳ[J]. Navigation of China, 2018, 41(4): 53-56.

[32] 王冰. 基于多目标遗传算法的散杂货港口船舶调度系统研究[D]. 北京: 北京交通大学, 2014: 9-67.

WANG Bing. Research on Ship Scheduling System of Bulk Cargo Port Based on Multi-Objective Genetic Algorithm[D]. Beijing: Beijing Jiaotong University, 2014: 9-67.

[33] 侯春晓, 许劲松, 杨荣武. 内河无人船局部路径规划和循迹控制[J]. 船舶工程, 2017, 39(6): 41-45.

HOU Chun-xiao, XU Jin-song, YANG Rong-wu. Local Path Planning and Path Following Control for Inland Water USV[J]. Ship Engineering, 2017, 39(6): 41-45.

Scheduling Optimization of Shipping Logistics Port Based on AIS Data

BAI Xiang-en, LI Bo-han, XU Xiao-feng, XIAO Ying-jie

(Merchant Marine College, Shanghai Maritime University, Shanghai 201306, China)

The work aims to study a more effective scheduling scheme to deal with the complex waterway waters and dense logistics traffic flow in Ningbo Zhoushan Port area, to minimize the scheduling time and waiting time, that is, to maximize the efficiency. The navigation situation of Zhoushan Port in Ningbo was analyzed. The problems existing in the complex waterway area were put forward. A multi-objective function was proposed to minimize dispatching time and waiting time, a ship dispatching model for the complex waterways was established. In view of a large number of AIS data for ships, a waterway area scheduling model based on neural network was constructed, and speed change and ship prediction models were established for ships of different types and sizes to realize the prediction of ship scheduling status. An improved ship scheduling algorithm based on traditional particle swarm optimization was designed. The results showed that the model was solved by the algorithm and the traffic congestion could be judged and ship scheduling could be carried out based on different captains and spacing. Once possible congestion was predicted through the model, small vessels should pass through from the Tiaozhou Men channel and large vessels should pass through from the Xiasi Men channel and avoid congestion as much as possible. The model and algorithm can effectively improve the efficiency of ship scheduling and provide a theoretical basis for optimization of complex scheduling in shipping logistics ports.

complex waterway; deep neural network; particle swarm optimization; ship scheduling; AIS data

U652.1+2

A

1001-3563(2023)05-0211-11

10.19554/j.cnki.1001-3563.2023.05.027

2022−04−16

国家自然科学基金面上项目（42176217）

白响恩（1984—），女，副教授，主要研究方向为通航安全评估、港航论证和极地航行等。

徐笑锋（1986—），男，博士后，主要研究方向载运工具及其应用工程。

责任编辑：曾钰婵