基于弹塑性理论的软岩隧道最大变形量预测方法研究
2023-03-15赵昀马秋峰
赵昀,马秋峰
(1.中南勘察设计院集团有限公司,武汉 430074;2.山东理工大学资源与环境工程学院,淄博 255100)
隧道一旦开挖后,原岩应力平衡状态被打破,隧道围岩失去原有支撑,向已开挖的空间发生移动变形。针对软岩隧道变形量大的特点,需要一个能量释放的过程,以有效的减小支护结构的载荷、降低支护成本并提高支护结构的安全性。然而过大围岩变形将会导致隧道边缘的节理裂隙发育、贯通,甚至是围岩发生失稳。因此,准确预测隧道围岩的最大变形量将有利于选择合适的支护时机,同时确保隧道的稳定性。
学者们对隧道开挖后的变形特征与力学响应开展了大量研究。张常光等[1-2]、高永涛等[3]通过分析、归纳常用的岩土强度准则,推导了理想弹塑性岩体中隧道的应力场与位移场,并对常用强度准则进行了评价。苏雅等[4]针对软弱岩层隧道开挖后的力学响应,推导了隧道围岩稳定极限变形的估算公式,并对影响因素进行了敏感性分析。刘杰等[5]探究了浅埋偏压隧道软硬交互水平层状围岩压力的分布情况,分析了硬岩与软岩层厚比对隧道围岩压力分布的影响规律。Zhang等[6]、陈有亮等[7]基于Fick第二定律与非关联塑性流动法则,推导了软岩遇水隧道应力和位移解。王志龙等[8]利用岩土控制变形分析方法,分析了围岩级别、地应力等多个因素对围岩变形的影响。邱明明等[9]分析了浅埋偏压赋存条件隧道的大变形特征,并给出了防治措施和加固方案。王明年等[10]基于双线性准则,推导了隧道弹塑性位移和应力解析解,并分析了各因素对应力场和位移场的影响。贺耕夫等[11]建立了衬砌-正冻围岩-未冻围岩简化力学模型,基于Hoek-Brown准则推导出了圆形隧洞理想弹塑性围岩的塑性区半径解析解。任汀等[12]建立了考虑时间效应的非线性本构方程对TBM施工隧道围岩变形与地表沉陷进行了计算,与现场实测结果一致。李小丰[13]基于Massinas和Sakellariou解发展了隧道弹塑性解,并给出了临近应力和塑性区半径解的新方法。付睿聪等[14]考虑了加载实际历史对隧道围岩应力场和位移场的影响,通过有限元软件进行对比,认为不考虑加载历史得到的位移和塑性区将小于实际情况。
目前,基于强度理论推导隧道围岩应力场与位移场研究取得了较为丰硕的成果,然而无论在现场支护时机的选择,还是安全性分析过程中,隧道边缘最大变形量都是非常重要的参数[4,15-16]。鉴于此,基于松动圈剪切滑移理论,利用Hoek-Brown准则推导得到最小支护应力,将其代入隧道边缘径向位移公式,给出了圆形隧道边缘最大变形量的求解方法。通过对比现有数值计算方法,探究本文方法的准确性与合理性,最后分析各个力学参数对最大变形量的影响特征。研究成果将为预测隧道边缘最大变形量提供一种有效的计算方法。
1 软岩隧道让压支护的变形理论
1.1 软岩隧道的变形理论
假设在深度为H位置开挖一条半径为r0的圆形隧道,围岩的弹性模量为E,泊松比为v,剪切模量为G。同时假设远场应力σ0为静水应力场。尽管大多数情况下远场应力为非对称应力场,但文献[1,5]中指出软弱岩层无法承受较大的应力差,将软弱岩层中的应力场近似为静水应力场是可以接受的。同时假设围岩材料为弹塑性体,且满足Hoek-Brown准则。
如图1所示,隧道开挖后,由内向外依次呈现以下4个区域:松动区、塑性区、弹性区和原始应力区。
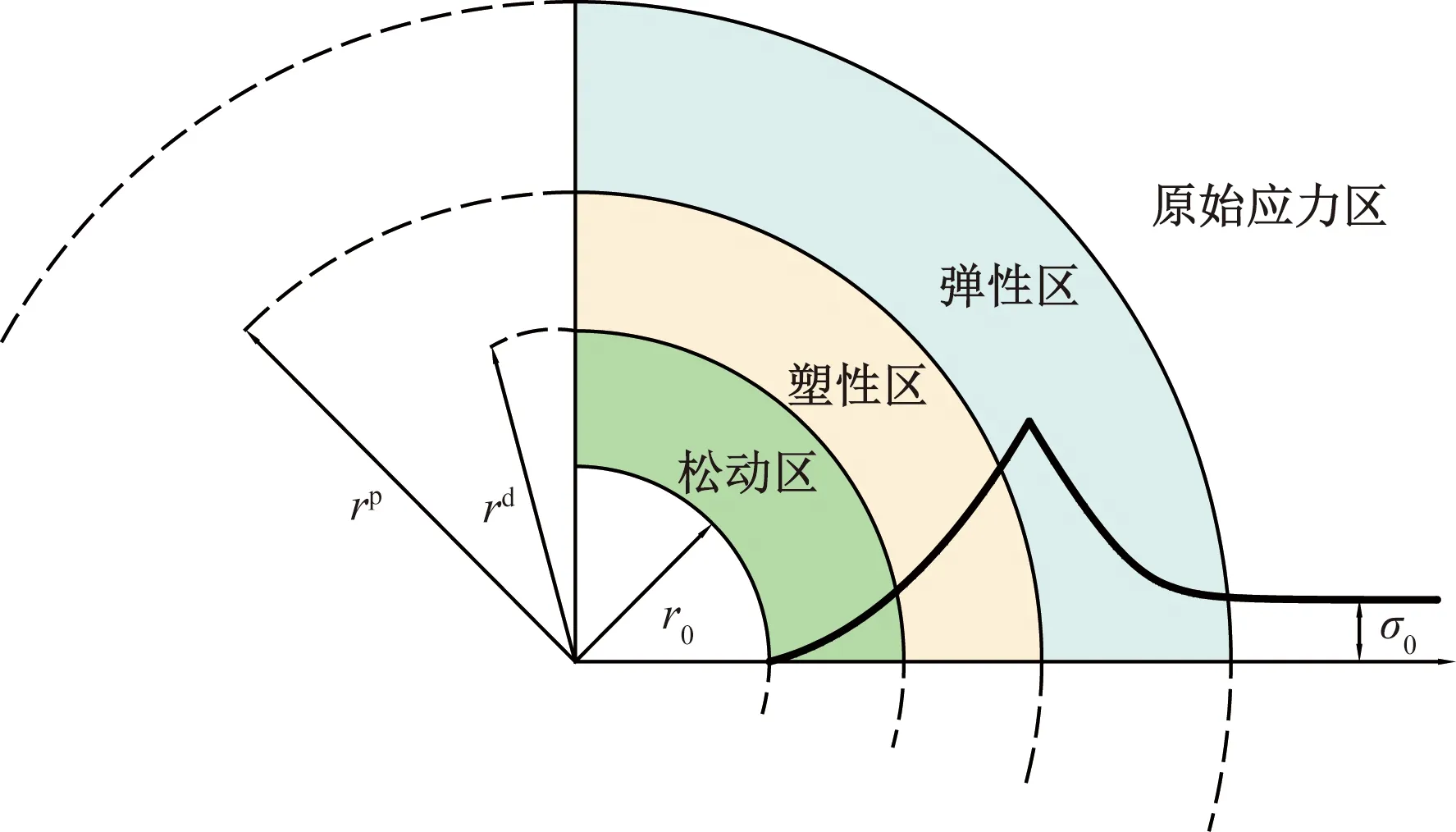
隧道的半径为r0;松动区的半径为rd;塑性区的半径为rp
根据Hoek-Brown准则[17],其表达式为
(1)
式(1)中:σ1、σ3分别为最大、最小主应力,MPa;σci为完整岩石的单轴抗压强度,MPa;mb、s、α为Hoek-Brown准则相关参数,其表达式分别为
(2)
(3)
(4)
式中:mi为反映岩石的软硬程度的参数;GSI为地质强度指标;D为扰动参数,介于0~1。
基于Hoek-Brown准则,Carranza-Torres[18-19]推导隧道边缘径向位移量ux的计算公式为
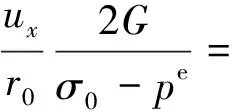
(5)
式(5)中:r0为开挖隧道的半径,m;G为剪切模量,GPa;σ0为远场应力,MPa;pe为保持围岩弹性状态的支护应力,当支护应力psp大于pe时隧道围岩将保持弹性应力状态,MPa;v为泊松比;P为归一化临界应力;S0为归一化的天然应力;rp为塑性区半径,m。
式(5)中,S0、P、pe和rp的表达式分别为[18-19]
(6)
(7)
(8)
(9)
式中:psp为支护应力,MPa。
通过式(5)~式(9)可以看出,影响隧道边缘径向位移ux的因素主要分为三类:远场应力σ0、围岩力学参数和支护应力psp。
1.2 基于Hoek-Brown准则的最大变形量
在极坐标条件下,根据静力平衡方程
(10)
式(10)中:r为半径,即该点位置距圆心的距离,m;σr为径向应力,MPa;σθ为环向应力,MPa。
由于松动圈岩石满足Hoek-Brown准则,同时将σr视为最小主应力,σθ为最大主应力。根据式(10)和式(1)可得
(11)
式(11)中:C为积分常数项。
根据边界条件,在隧道边缘,r=r0位置,径向应力等于支护应力,σr=psp,因此得到C的表达式为
(12)
将C代入式(8),进一步整理得到径向应力σr的表达式为
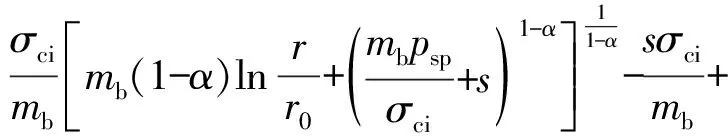
(13)
得到径向应力σr后,代入Hoek-Brown准则[式(1)]中可得出环向应力σθ的表达式为
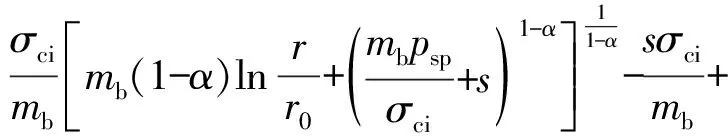
(14)
至此建立了基于Hoek-Brown准则的隧道围岩塑性区应力场公式。为了求解最大变形量。从式(2)中可知,当隧道条件一定的情况下,支护应力越小,变形量越大。但过小的支护应力将会带来安全隐患。利用松动圈剪切滑移理论确定最小支护应力,进而计算最大变形量。
根据让压支护理论[20-21],随着隧道边缘变形量的增加支护应力呈现先减小后增大的趋势。隧道开挖后随着变形量增加隧道围岩内部能量释放,所需的支护应力逐渐减小。进一步继续增大隧道边缘的变形,围岩内部的节理裂隙发育、贯通,支护应力将增大。因此必然存在一个最小支护应力。
根据松动圈剪切滑移理论[22],假设松动圈内部存在一定量的随机节理,由圆形隧道的对称性和应力场公式可知,环向应力即为最大主应力,径向应力为最小主应力。
如图2所示,取任意单元,假设内部存在一条节理,节理方向与径向应力方向的夹角加设为α。采用τj和σnj分别表示节理面上的正应力和剪应力,根据受力条件,正应力和剪应力的表达式分别为
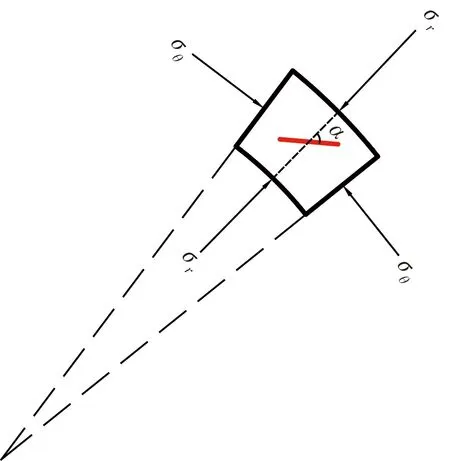
图2 含节理单元示意图
(15)
(16)
同时假设抗剪强度τmax为
τmax=fσα+c0
(17)
式(17)中:f为摩擦系数,f=tanφj,其中φj为节理面摩擦角,(°);c0为节理黏聚力,MPa。
根据剪切滑移准则,当剪应力超过抗剪强度τmax时,节理发生剪切滑移,因此发生剪切滑移的条件为
(18)
借助于莫尔圆,如图3所示。利用图3能够确定优先发生剪切滑移的裂纹角度αd(根据对称性)为
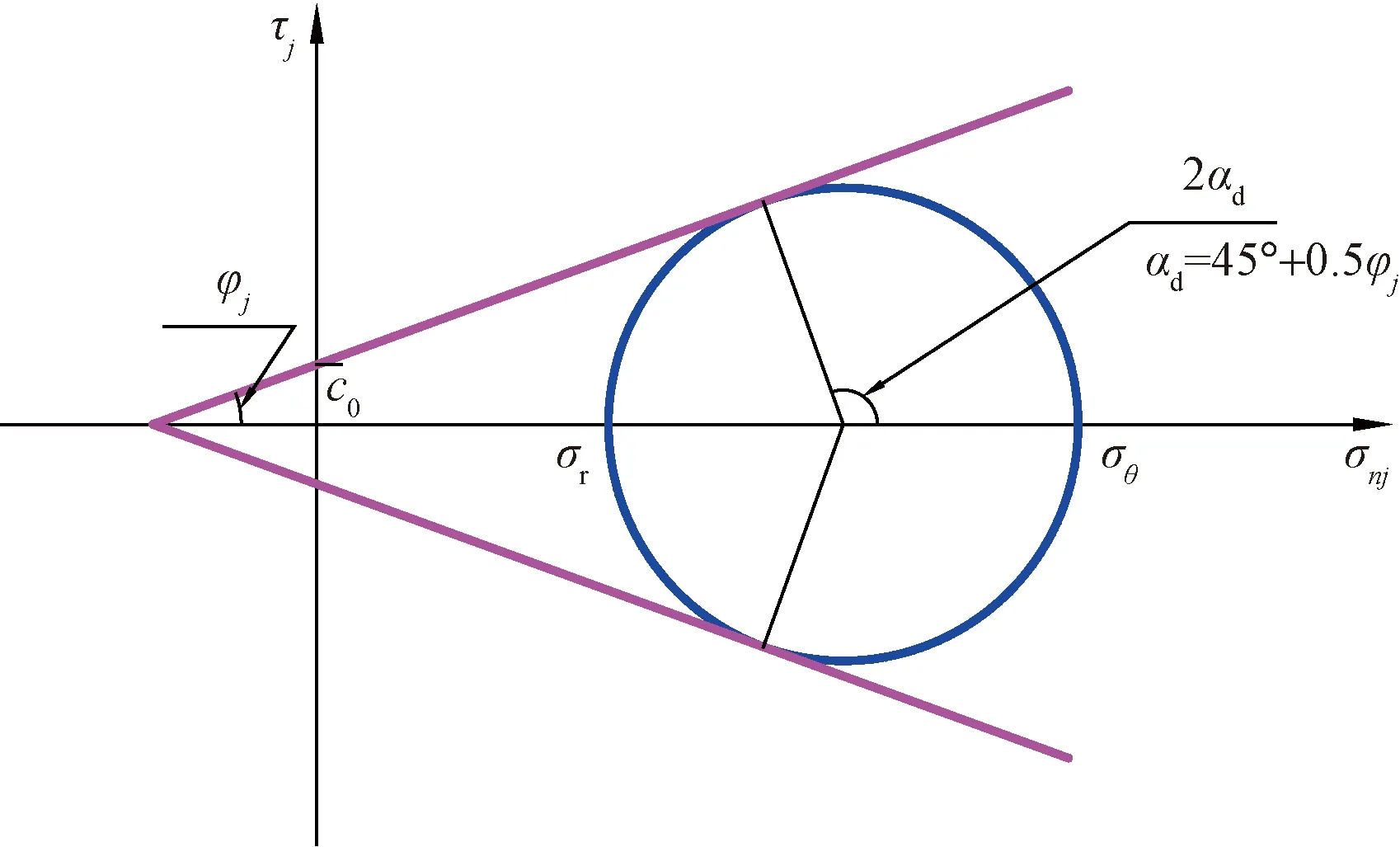
τj为节理面上的剪应力;φj为节理摩擦角
(19)

(20)
式(20)中:等号左侧为单位长度隧道所受到的支护力;等号右侧为单位长度隧道圆心上方松动区岩体的质量。
(21)
式(21)中:γ为围岩重力密度,kN/m3。
根据定义环向应力σθ等于远场应力σ0所处的位置定义为松动区边界,即当r=rd时,有σθ=σ0,代入式(21)得
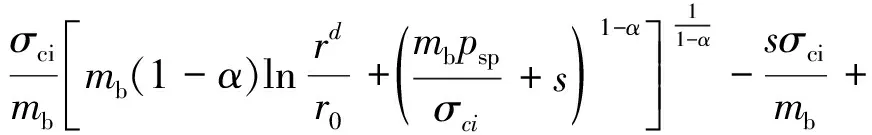
(22)
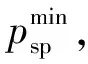
2 计算方法验证
2.1 弹塑性应力场验证
对所推导结果进行验证,将本文结果与现有研究进行对比。文献[23]中基于Hoek-Brown准则给出了弹塑性应力场理论解答,根据算例中的工况,圆形隧道半径r0= 4 m,埋深为200 m,覆岩重力密度γ=0.027 kN/m3,因此远场应力σ0= 5.4 MPa。岩石力学参数与算例中保持一致,如表1所示,假设存在0.1 MPa支护应力情况下,塑性应力场计算结果与文献[23]的对比结果如图4所示。可以看出,本文结果与文献[23]的结果一致,证明本文关于塑性区应力场推导的准确性。

表1 岩体参数表[23]
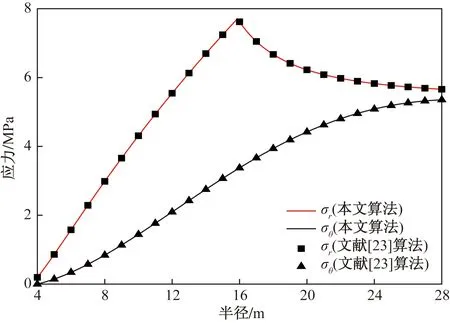
图4 应力分布对比
2.2 塑性区半径验证
采用2.1节中的工程背景,对不同支护应力条件下塑性区半径进行计算,计算结果与文献[23]中的计算结果进行对比,结果如图5所示。可以看出,本文计算结果与文献[23]中的塑性区半径一致,证明了本文结果的合理性与准确性。
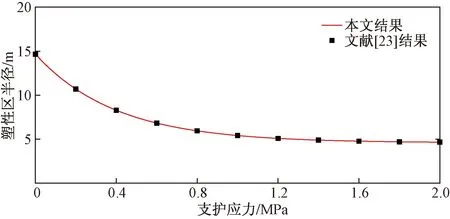
图5 塑性区半径对比
2.3 最大位移量验证
鉴于Vlachopoulos等[24]的研究中关于隧道最大变形量的研究已经得到了证实,且与本文算法一致采用了Hoek-Brown准则,因此利用文献[24]中的计算方法对本文算法进行验证。其工程背景如下:隧道半径r0=4 m,远场应力σ0=28 MPa,给出了两类岩体中的隧道变形结果,分别称为Case1和Case2,其岩体参数如表2所示。最大位移量的计算对比结果如表3中所示。
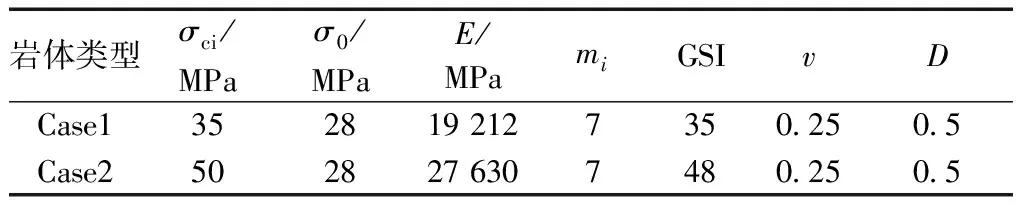
表2 岩体参数[24]
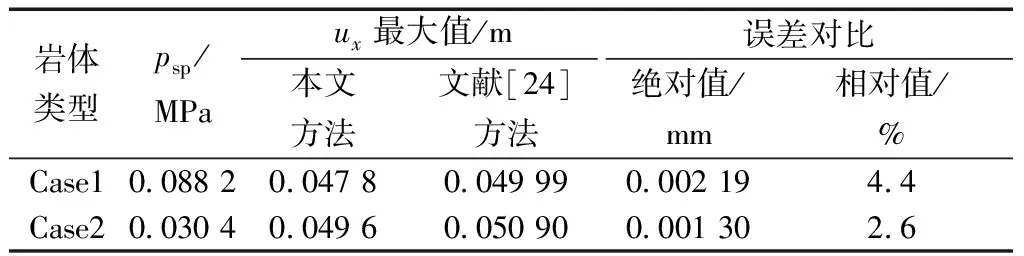
表3 两种方法计算结果对比
分别对Case1和Case2进行计算,根据支护应力psp利用本文方法对最大变形量uxmax进行计算。然后利用文献[24]中的方法进行数值计算,从计算结果可以看出,两种工况下误差分别为4.4%和2.6%,表明两种方法的计算结果具有较好的一致性,证明了本文方法的合理性。
3 参数分析与讨论
通过对隧道最大变形量uxmax的推导可知,uxmax的影响因素主要包括:远场应力σ0、岩体地质强度指标GSI、岩石单轴抗压强度σci、弹性模量E、泊松比v和H-B模型中的参数mi。分别取GSI=20、30、40、50和60的不同岩体,对上述参数进行敏感性分析。在对某个参数进行敏感性分析时,其他参数如表1、图6所示。
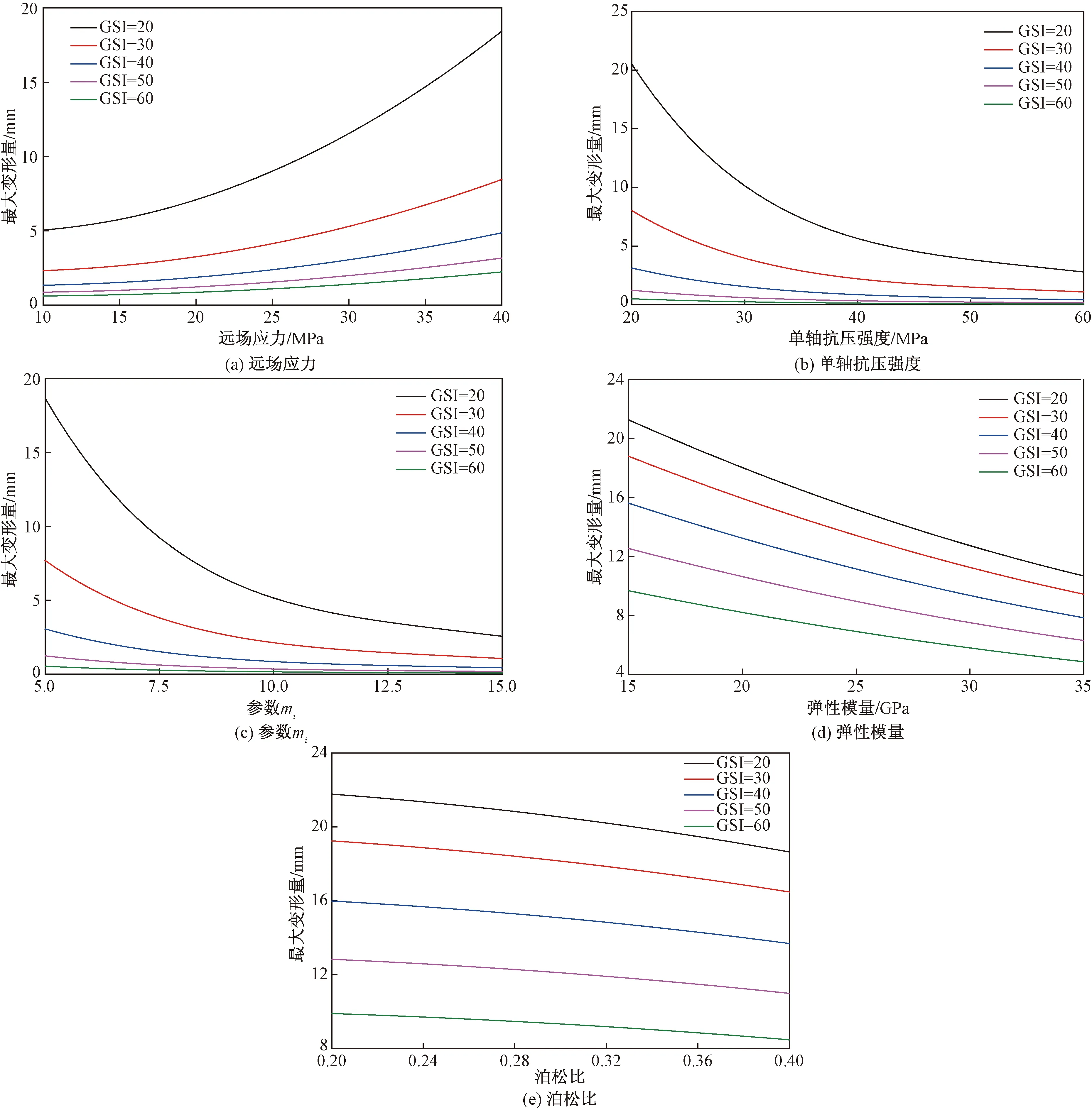
图6 隧道最大变形量关于各参数的敏感性
图6(a)给出了隧道边缘最大变形量与远场应力σ0的关系。可以看出,当GSI一定时,σ0与uxmax呈现正相关,曲线呈现上凹型曲线,说明随着远场应力σ0的增大,最大变形量增长量越大。通过对比不同GSI,当GSI=20时,远场应力从10 MPa增长至40 MPa过程中,uxmax增长了13.3 mm,平均增长率为0.44 mm/MPa,GSI分别为30、40、50和60时,平均增长率为0.21、0.12、0.076、0.05 mm/MPa。可以看出,随着GSI的增长,uxmax对σ0的敏感性逐渐减弱。当地质强度指标较小时,应关注远场应力对隧道边缘变形量的影响;当地质强度指标较大时,可近似将变形量视为常数。
图6(b)、图6(c)分别为单轴抗压强度σci和参数mi对隧道最大变形量影响敏感性分析,可以看出,σci和mi对uxmax均呈现负相关。由图6(b)可知,σci与uxmax呈现上凹形曲线,说明随着单轴抗压强度的增大最大变形量减小且减小速率越来越慢。对比GSI分别为20、30、40、50和60时,平均降低率为0.44、0.18、0.06、0.027、0.010 mm/MPa,说明随着GSI的增大,σci对uxmax的敏感性降低,特别是当GSI超过40后,σci对uxmax变得不再敏感。如图6(c)所示,参数mi对uxmax的敏感性规律与σci类似,不再赘述。
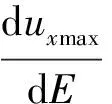
4 结论
基于Hoek-Brown准则建立了软岩隧道的最大变形量估算方法,分析了各个影响因素对最大变形量的影响规律,得出如下结论。
(1)基于Hoek-Brown准则推导了塑性区应力场,得到松动区尺寸关系式,引入剪切滑移准则,推导得到了最小支护应力,代入Carranza-Torres位移公式,建立了软岩隧道的最大变形量估算公式。
(2)利用现有研究成果对本文推导过程和计算结果进行验证,结果显示本文方法计算得到的最大变形量与文献结果的相对误差均小于5%,证明了本文估算方法的合理性与准确性。
(3)最大变形量与远场应力σ0呈现正相关,与单轴抗压强度σ0、参数mi呈现负相关。随着地质强度指标GSI的增加,最大变形量关于σ0、σci、mi的敏感性均呈现减弱的趋势,当GSI较大时(超过40时),最大变形量可近似视为常数。
(4)最大变形量与弹性模量E、泊松比v呈现负相关,随着地质强度指标GSI的增大,最大变形量与E之间以及最大变形量与v之间的敏感性并未产生显著的改变。
