高维数据组合关联关系挖掘方法
2023-03-15姜建武王博
姜建武, 王博
(1.桂林理工大学测绘地理信息学院,桂林 541004;2.生态时空大数据感知服务重点实验室,桂林 541004)
关联规则挖掘(association rule mining,ARM)是数据挖掘的主要任务之一[1],也是数据挖掘领域最重要、最活跃的研究领域[2]。其中,提高挖掘效率和降低挖掘结果的冗余度是其需要解决的两个核心问题[3-7]。围绕以上问题,广大学者开展了一系列研究。曾子贤等[8]基于Apriori算法提出了改进的MIFP-Apriori(matrix improved frequent pattern-Apriori)算法,从矩阵、改进频繁模式树和计算候选集频数优化策略3个方面入手,解决Apriori算法挖掘效率低,候选集冗余的问题。Rathee等[9]提出了一种基于Spark平台的分布式关联规则挖掘算法Adaptive-Miner,该算法是一种动态关联规则挖掘算法,可以实现对海量事务的关联规则挖掘。Czibula等[10]提出了一种关系规则挖掘算法CRAR(concurrent relational association rule mining),通过采用并发技术降低挖掘时间。Yan等[11]提出了一种用于定量关联规则挖掘的并行粒子群优化(particle swarm optimization,PSO)算法,提供面向粒子和数据两种不同的并行挖掘方式,并通过实验验证了该方法在大型事务数据集中挖掘中更具通用性。杨媛等[12]针对传统数据挖掘效率低、耗时的问题,提出了一种新的多层次分布式网络数据挖掘改进方法,并给出了多层次分布式网络结构。Chiclana等[13]设计了一种新的基于动物迁移优化的挖掘算法ARM-AMO(association rule mining-n animal migration optimization)以减少关联规则的数量,其原理是从数据中删除支持度不高且不必要的规则,具体实现是在频繁规则挖掘时添加适应度函数,用以减少相关模式的生成。Harikumar等[14]通过对Apriori算法进行改进,达到在高维、海量数据上高效挖掘的目的,且能够从高维数据中找出只与重要属性相关的关联规则。现有的关联规则挖掘算法依赖于基于频率的规则评估方法[15],如支持度和置信度[16],无法为规则评估提供良好的统计或计算方法,并且经常存在大量冗余规则[17-20]。针对该问题,Song等[21]提出了一种基于交叉验证的可预测性集合类关联规则挖掘方法,通过实验验证,该方法在挖掘到大量有用规则的同时,性能优于现有的一些算法。王京等[22]提出了一种基于相互关联规则的KAFP-Growth(key attributes frequent pattern growth)算法,通过在FP-Growth(frequent pattern growth)算法的基础上引入重要属性概念对挖掘算法进行改进,减少了频繁项集,提高了计算性能。杨岚雁等[23]针对MLKNN(multi-label k-nearest neighbor)算法忽略现实世界中标签之间的相关性问题,基于FP-Growth挖掘标签之间的相关性进而改进MLKNN算法。廖孟柯等[24]针对传统Apriori算法时间复杂度高、计算效率低的问题,提出一种基于三维矩阵的Apriori优化算法,通过建立三维矩阵和简约数据库的方式较少计算冗余,提升关联规则的挖掘效率。
但是,以上研究在提升高维数据的挖掘效率和降低规则的冗余度方面还存在一些不足。为解决该问题,提出一种适用于高维数据的组合关联关系挖掘算法(mining multidimensional association rules by combination, Marc),在挖掘之初实现对样本数据的筛选,降低弱样本的干扰,提升关联规则挖掘的聚焦度。通过引入数据整体分布的概念,计算分布系数和删除阈值,增加数据筛选过程,并构建样本关系表,联合用户设置的最小支持度和最小置信度共同对数据进行挖掘。通过构建Marc算法,为海量、高维数据的高效挖掘提供一种新方法。
1 Marc算法原理
Marc算法主要解决高维数据的挖掘问题,与常规算法不同,Marc算法的优点如下。
(1)初读数据时增加二次筛选,降低弱样本影响。对原始样本进行筛选是提升挖掘效率的关键步骤[25]。Marc算法引入样本集分布系数和删除阈值两个指标,在数据初次读取时,根据样本的分布情况对初始样本增加二次筛选,保留样本的出现频数必须同时满足大于最小支持度和删除阈值,该步骤有利于减少弱频繁项和弱关联规则的数量,从而提升数据挖掘的效率,降低规则的冗余度。
(2)根据样本关系表重构样本组合,降低算法复杂度,提升挖掘效率。与常规关联规则挖掘算法的挖掘方式不同,Marc算法通过构建样本关系表,然后根据该关系表对样本集里的样本进行全排列组合,从而将样本间的关联关系转换为关系组合,再对组合后的样本进行挖掘进而获得关联规则。经实验验证,相较于对比算法,Marc算法在处理高维数据挖掘时占用内存更小,挖掘的复杂度更低,挖掘效率更高。
1.1 算法相关指标
(1)设项集x=[x1,x2,…,xp]代表一组项,I=[I1,I2,…,Im]是一个事务数据集,I中的每个Ii(i∈[1,2,…,m])是包含x中项的一组事务。A和B表示包含x中项的两个模式。
(2)Supp(支持度)表示同时包含A和B的事务占所有事务的比例,可表示为
(1)
(3)Conf(置信度)表示使用包含A的事务中同时包含B事务的比例,即同时包含A和B的事务占包含A事务的比例,可表示为
(2)
(4)Dist(分布系数)用于标定样本的离散程度,Marc算法的分布系数采用SigMod对样本的方差或标准差规划获得。
(3)
式(3)中:k为样本的方差或标准差,具体选用根据实际需要确定。
(5)Trim(删除阈值)由分布系数Dist与样本均值E的乘积得到,主要用于去除样本中的弱频繁项。
Trim=DistE
(4)
1.2 算法步骤
Marc算法的核心思想是在数据筛选时加入数据整体分布的考量,并构建样本间的关系表,以该关系表为基础对样本数据重新组合,挖掘频繁项和关联关系。Marc算法的挖掘流程如图1所示。
图1中主要包括样本二次筛选、样本频次统计及排序、样本关系表生成、样本全排列组合以及频繁项和关联关系生成5个步骤,具体如下。

图1 Marc算法流程图
步骤1读取数据统计样本频次,根据最小支持度和计算出的删除阈值对原始数据集进行筛选,并按照样本频次对数据集降序排列,该步骤可以提升因支持度设置不合理引起的挖掘结果冗余。
步骤2对排序后的数据集进行扫描,记录单个样本以及单个样本出现的次数形成样本频数集合,接着,将样本频数集合里的样本两两组合,分别统计样本组合的出现次数,将小于最小支持度的样本组合删除,形成样本组合频数集。
步骤3根据样本组合频数集生成样本关系表。
步骤4扫描第一步生成的排序后数据集,根据样本关系表将样本重新全排列组合,形成新的样本数据集。
步骤5扫描步骤4的数据集,统计组合样本的频次,计算组合样本的支持度和置信度,生成频繁项和频繁模式。
Marc算法的详细步骤如下。
步骤1设定最小支持度为min_support,最小置信度为min_confidence,为便于后续对算法计算过程进行阐述,对2.1节项集x和事务集I做式(5)、式(6)修改。
I=[I1,I2,I3,…,Im]T
(5)
Ii=[xi1,xi2,…,xij]
(6)
式中:1≤i≤m;1≤j≤p。
如式(5)、式(6)所示,将事务数据集I变换为m行p列的数组,Ii中的xij为事务数据集I中第i行的第j个项,xij∈x。
步骤2遍历样本集合I,计算样本集合内每一个样本xij的频数Nij(即该样本在样本集中的出现次数),设样本总数为M。
(7)
(8)
式中:Nij为x中的某个项在事务数据集I中出现的次数;M为x中所有项在事务数据库I中出现次数之和;Count()为统计函数。
统计每个项出现次数的目的是为了计算后面的分布系数和删除阈值,去除弱样本的影响。
如图2所示,统计事务数据集中每个样本的出现次数并进行降序排列。

图2 样本频数统计并排序
步骤3计算样本频数的平均值E、方差σ2及标准差S,计算公式分别为
(9)
(10)
(11)
步骤4计算分布系数Dist。采用SigMod函数对标准差或者方差进行规划,计算公式为
(12)
式(12)中:Index∈(S,σ2)。
由于方差和标准差反映了样本的离散程度,因此可以以此为指标对原始样本进行筛选,通过SigMod进行规划的目的是将该样本的离散度规划为[0,1],这样在求解删除阈值时更加方便。具体选用何种指标计算分布系数,可根据实际情况确定。需要注意的是,由于SigMod的变量取值范围较小,如图3所示,当变量值小于-6或者大于6时其结果都非常接近1,因此为了更好地筛选样本,当样本方差较大时,建议选择方差,当样本方差较小时选择标准差。
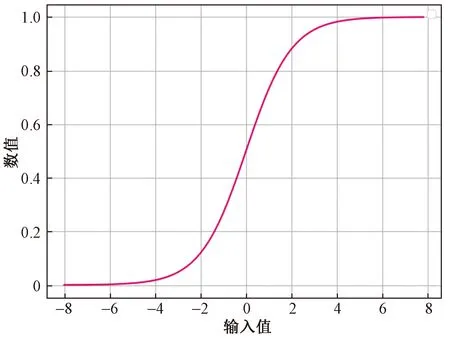
图3 SigMod函数变化曲线
步骤5计算删除阈值Trim,将样本集合中所有Nij小于Trim的样本删除,得到新的样本集合I′。
Trim=EDist
(13)
步骤6遍历样本集合I′,计算样本内每一个样本xij的出现次数N′ij,形成样本频数集Samples,设不同样本xij的总数为M′,由于删除了一些样本数据,因此此时的样本数和维度均小于或等于原样本数和维度,新的样本数记为m′,维度记为p′。
(14)
式(14)中:1≤i≤m′;1≤j≤p′。
(15)
Samples=[{s1:c1},{s2:c2},…,{si:ci}]
(16)
式(16)中:si为第i个样本;ci为第i个样本的频数,1≤i≤p′。
步骤7将Samples集合中的样本进行两两组合形成新的集合,记为S′amples,并统计组合样本在集合I′中共同出现的频数,将频数小于最小支持度的样本组合删除。
S′amples=[{si1:ci1},{si2:ci2},…,{sij:cij}]
(17)
式(17)中:sij为第i个样本与第j个样本组合;cij为第i个样本与第j个样本共同出现的频数,1≤i≤p′,1≤j≤p′,i≠j。
步骤8根据S′amples集合,生成样本关系表Relations,具体生成方法是以组合样本中某一个样本为基础,找出所有与之相关的样本即在S′amples集合中存在,可表示为
Relations={s1:[s2,s3,…,si],s2:[s1,s3,…,si],…,si:[s1,s2,…,si-1]}
(18)
步骤9根据样本关系表Relations对I′中的每一组样本进行全排列组合,具体方法是以I′中的某一样本为基础,遍历I′中的其他样本,若样本在基础样本的关系表中,则进行组合,循环I′中所有样本,形成全排列集合I″,此时I′中的每一组数据的维度可能会急剧扩大,设此时样本的数量为m″,维度为p″,新样本集合可表示为
I″=[I″1,I″2,…,I″m]T
(19)
I″i=[x′i1,x′i2,…,x′ij]
(20)
式(20)中:1≤i∈m″;1≤j≤p″。
x′ij=[xi1,xi2,…,xip′]
(21)
即此时的x′ij是由多个xij组成的,m″=m′,p″≥p′。
步骤10遍历样本集合I″,计算样本内每一个样本x′ij的出现次数N″ij,形成新的样本频数集S′amples。
(22)
式(22)中:1≤i≤m″;1≤j≤p″。
(23)
S′amples=[{s′1:c′1},{s′2:c′2},…,{s′i:c′i}]
(24)
式(24)中:1≤i≤p″。
步骤11根据S′amples计算I″中每个新样本x′ij出现的概率,记为Pij,计算不同样本间组合的支持度记为Supportij、置信度记为Confidenceij,将小于最小支持度和最小置信度的样本删除。
步骤12生成频繁项集合关联关系集,按照支持度、置信度降序排列。
以上步骤即为Marc算法关联规则挖掘的流程,其总体示意图如图4所示。
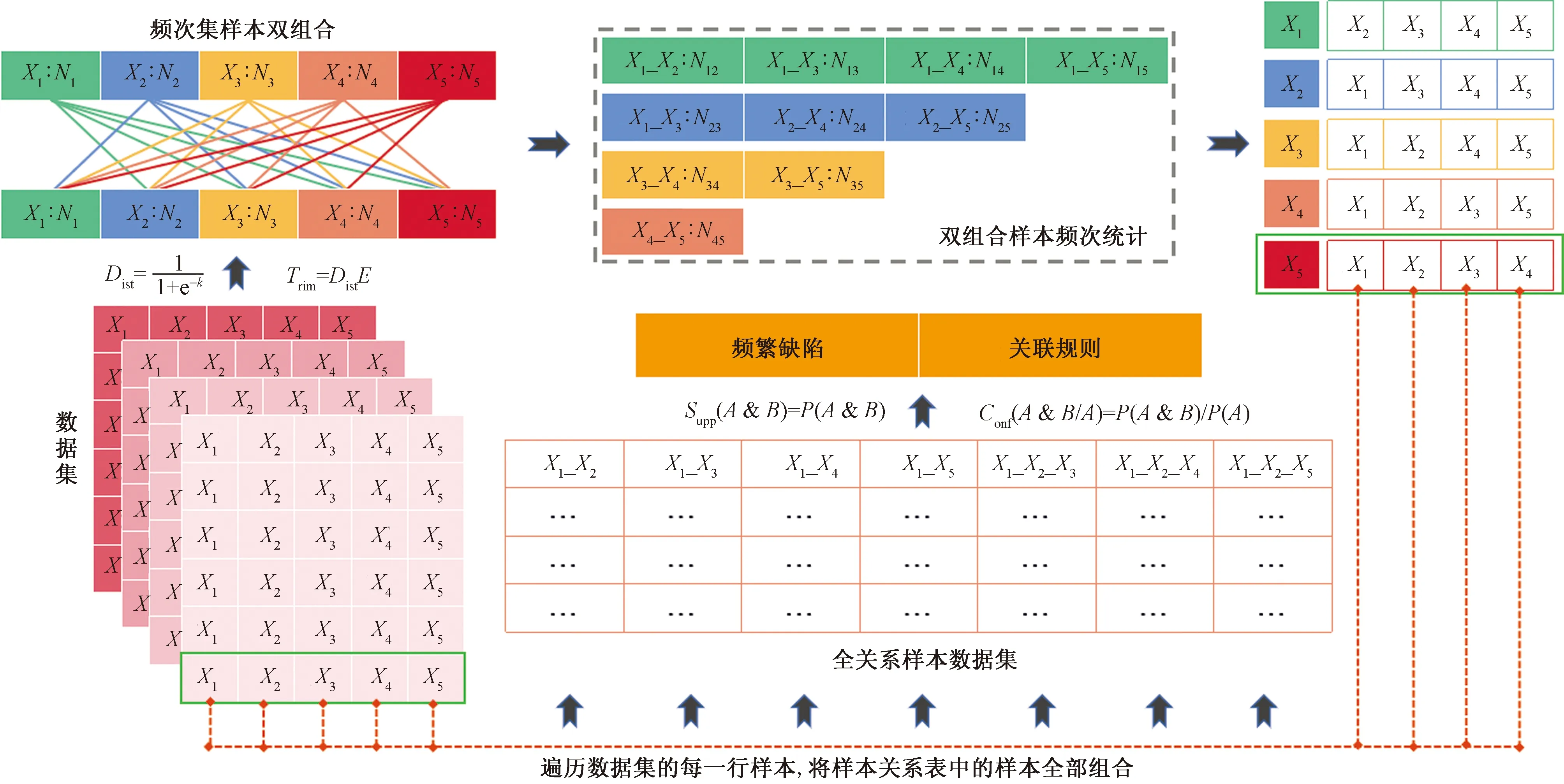
X1~X5为样本集中5个不同的样本;N1~N5为X1~X5在样本集中出现的次数;P为概率
时间复杂度是评价算法效率的重要参数,根据1.2节算法的过程,分析本文算法的复杂度如下。
(1)定义包含n个样本的集合I,时间为1。
(2)第一次遍历样本I计算频数,时间为n。
(3)计算删除阈值后对低于阈值的样本进行删除,形成新的样本集合I′,时间为n。
(4)遍历新的样本集合I′,统计新集合的样本频次,形成样本频数集Samples,时间为n。
(5)将Samples集合中的样本进行两两组合形成新的集合,记为S′amples,并统计组合样本在集合中共同出现的频数,时间为n2。
(6)根据S′amples集合,生成样本关系表Relations,由于每一个要素都需要与其他要素进行组合,因此时间为n2。
(7)根据样本关系表Relations对I′中的每一组样本进行全排列组合,形成样本集合I″,时间为n。
(8)根据S′amples计算I″中每个新样本x′ij出现的概率,时间为n。
综上所述,本文算法的时间总耗时为
T(n)=1+n+n+n+n2+n2+n+n
=1+5n+2n2
(25)
因此,本文算法的时间复杂度为O(n2)。
2 实验分析
2.1 实验环境及评价指标
2.1.1 实验环境
本实验选取的Python版本为3.8.5,实验平台的配置如表1所示。

表1 实验设备配置
为方便数据挖掘,本实验以支持度数代替支持度。本实验设置的最小支持度数为5,最小置信度为0.5。
2.1.2 评价指标
为验证所提算法在高纬数据关联规则挖掘时的效率提升及关联规则冗余度降低方面的优势,通过设计Marc与Apriori、FP-Growth和Eclat算法的对比试验,选取挖掘时间、内存消耗、产生的频繁项数量和关联规则数量4个指标评价所提算法的优略。
2.2 实验数据
关联规则挖掘的核心是从不规律的样本中挖掘出其蕴含的隐式关联关系。通过构建不同维度和事务数的数据集进行4种算法的对比实验,为充分对比分析四类算法在不同数据集上的表现,共构建对比数据集60组,数据集的具体构建方法如下。
2.2.1 数据集构建策略
为了使实验事务数据集中的项构成的关联规则模式聚焦,其生成遵循以下规则:①假设事务中下标奇数项与奇数项,偶数项与偶数项是相关的,生成事务集时按奇、偶交替生成;②设定事务集中包含的做多项数为dimension,每个事务中具有的项总个数最多为dimension个;③每个事务的噪声项个数为noise个,noise值随机设定且在0~3,噪声项的选取规则是当生成奇数项时噪声样本为偶数项,当生成偶数项时噪声样本为奇数项;④同一事务中包含的项是唯一的。
2.2.2 数据集构建与分片
定义样本集中每一行为一个事务,每个事务中包含的要素数为事务的维度。所构建的数据集最大维度为25,最多包含300个事务项。为了保证实验数据集中关联规则模式的一致性,首先按照2.2.1节所述的规则分别生成维度为10、15、20、25的包含300个事务项的数据集,然后按照每20个事务项对前面生成的数据集进行切片,即每个维度都包含事务项20~300的15个数据集。
2.3 实验结果与分析
采用2.1节所述的4个指标对所提算法与Apriori、FP-Growth和Eclat进行对比分析。实验结果如下。
2.3.1 挖掘耗时分析
四类算法在维度为25,事务项数量为300时的耗时如表2所示,不同维度和事务项数量下的挖掘耗时对比结果如图5所示。

表2 挖掘耗时
通过对表2和图5进行分析,可得出如下结论:①总体上四类算法的挖掘时间与维度和事务项数量成正比,且维度对挖掘时间的影响较大;②Marc算法较其他三类算法的挖掘耗时远远低于对比模型,且事务项数量越多,维度越高,Marc算法的时间优势越明显;③在挖掘时间随事务项数量和维度变化的增长率方面,Marc算法的增长率较对比算法是最小的。Marc算法和Apriori算法的挖掘时间增长率较FP-Growth和Eclat更为平稳,FP-Growth和Eclat随着事务项数量和维度的提升显著增加了挖掘时间,且波动性较大,表明在高维数据挖掘时,两类算法的稳定性较Marc和Apriori差。
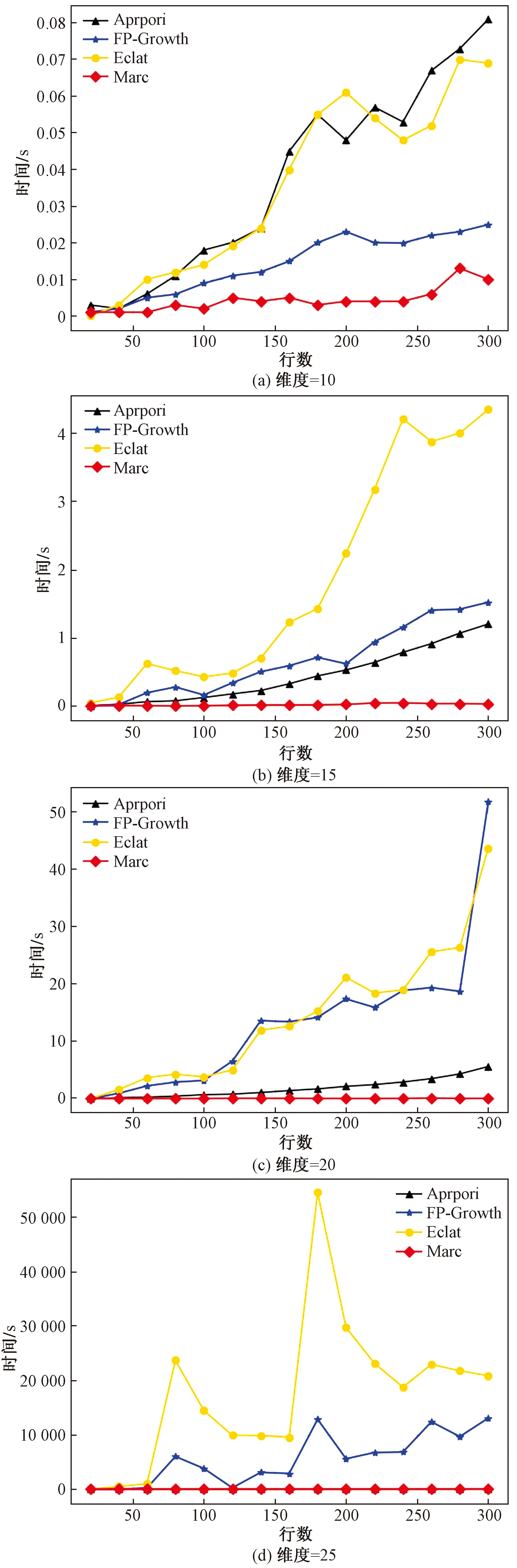
图5 挖掘耗时对比图
2.3.2 内存消耗分析
四类算法在维度为25,事务项数量为300时的内存消耗如表3所示,不同维度和事务项数量下的内存消耗对比结果如图6所示。
从表3和图6可以看出:①Marc挖掘时消耗的内存远远小于Apriori、FP-Growth和Eclat算法,且样本维度越高,Marc算法内存优势越明显;②在低维度数据挖掘时,由于Marc会生成样本关系表和全关系组合,因此会耗费更多的内存,高维度数据挖掘时,其他三种算法的数据组织形式耗费的内存远远高于Marc算法的关系表和全关系组合的数据格式,表明本文算法对于高维数据的挖掘在内存消耗上更有优势;③Marc算法的内存消耗增长率远小于其他三类算法,且随着样本维度和事务项数量的增加,Marc算法的内存消耗增长率趋于稳定,表明Marc算法在内存耗费方面较对比算法[如图6(d)所示,Eclat和FP-Growth算法的内存消耗波动较大]更稳定。

表3 内存消耗
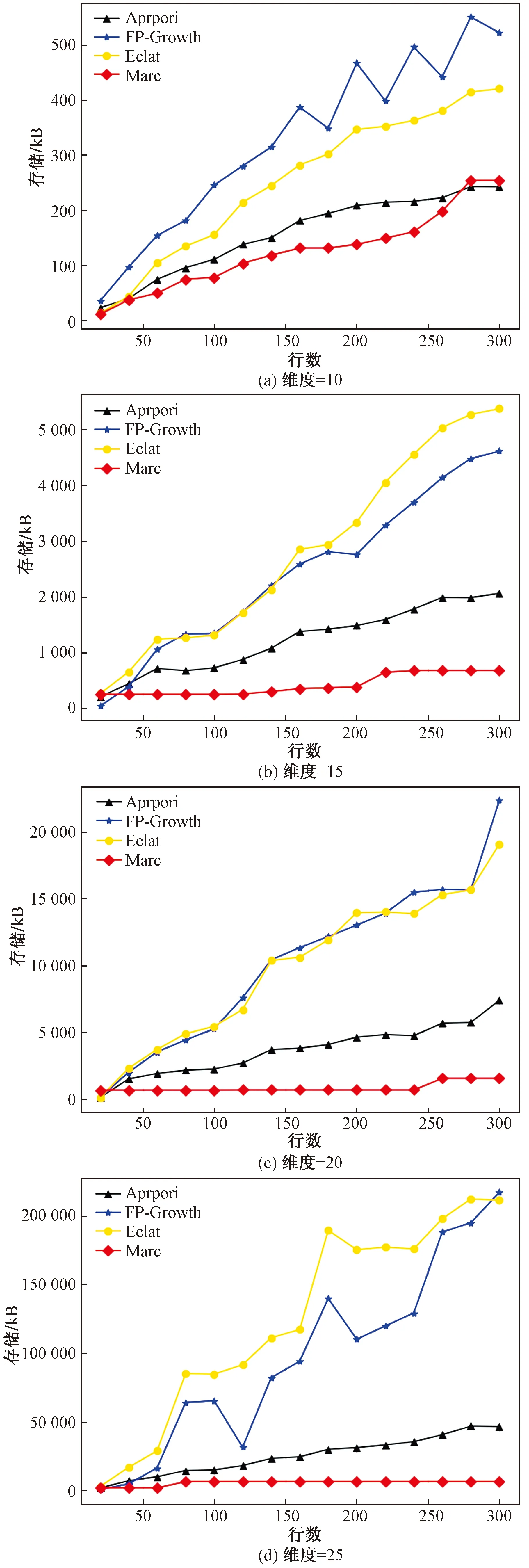
图6 内存消耗对比
2.3.3 频繁项数量分析
四类算法在维度为25,事务项数量为300时生成的频繁项数如表4所示,不同维度和事务项数量下生成的频繁项数对比结果如图7所示。

表4 频繁项数量
通过对表4和图7进行对比分析可知:①四类算法挖掘出的频繁项数量随着样本的维度和事务项数量的增加而增加,Marc算法挖掘出的频繁项个数较对比算法更少,挖掘结果更加聚焦;②同一维度下,随着事务项数量的增加,Marc算法挖掘出的频繁项个数趋于稳定,由于构建的数据集只有25个维度,因此Marc算法挖掘出的频繁项结果更符合数据集情况。
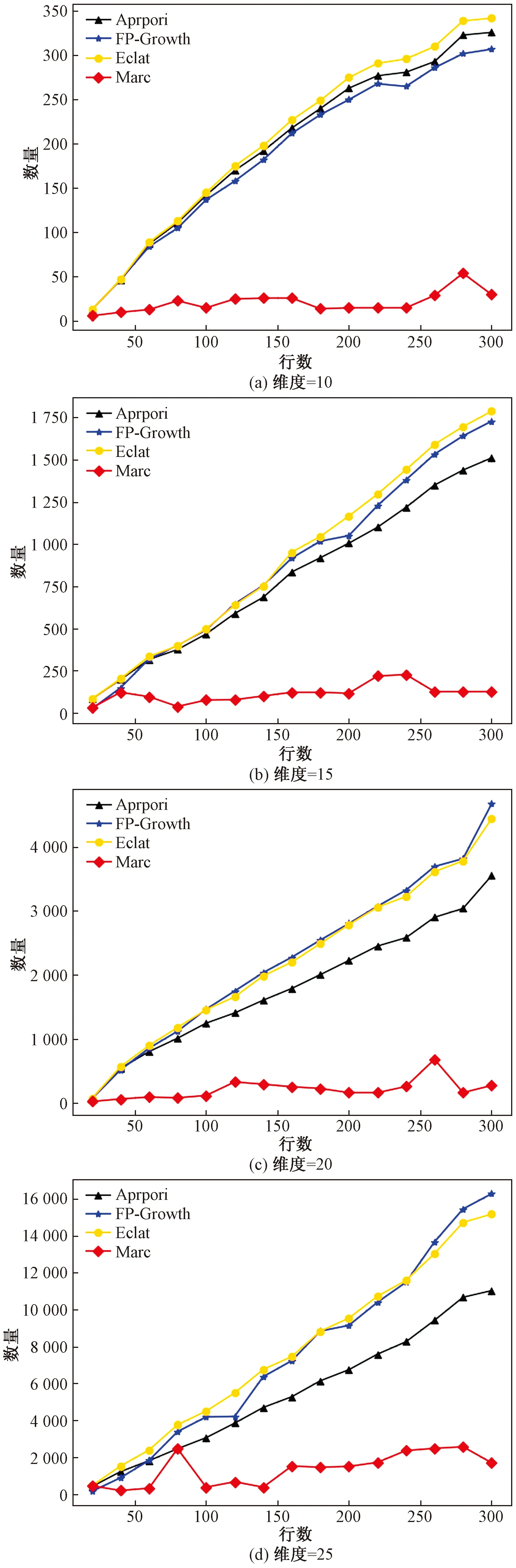
图7 频繁项数量对比
2.3.4 关联规则个数分析
四类算法在维度为25,事务项数量为300时生成的关联规则数如表5所示,不同维度和事务项数量下产生的关联规则数量的对比如图8所示。

表5 关联规则数量
由表5和图8可知,Marc算法在同一纬度下随着事务项数量的增加挖掘出的关联规则数量趋于稳定,较对比算法更加符合数据集的情况,Marc算法显著降低了关联规则的生成数量,且样本数量越多,挖掘出的关联关系越稳定。
2.4 挖掘精度评价
以上实验从挖掘时间、内存消耗、频繁项和关联规则数量4个方面评价了所提算法的优劣性,但是未对挖掘精度进行评价,因此,通过构建全关系样本验证随提方法的挖掘精度。所谓全关系样本是指每个事务项包含的维度和要素都一致的样本,构建的验证数据集每个事务项包含X1~X5维度,共5个事务项。设置最小支持度数为10,最小置信度为0.5。由于是全关系样本,因此所有关联关系的支持度和置信度都是1。实经实验验证,Marc挖掘出的频繁项数为31,关联规则数为128,且频繁项和关联规则与样本真实情况一致,挖掘精度为100%。
3 结论
Marc关联规则挖掘算法主要面向高维数据挖掘场景,经实验验证和对比分析,得出如下结论。
(1)Marc通过在数据初次筛选时引入分布系数和删除阈值指标,在挖掘的初期即简化了挖掘任务的时间和空间复杂度,大大提升挖掘算法的挖掘效率,节省了内存空间。
(2)Marc以样本关系表为基础构建样本全关系组合,简化了挖掘过程中维护的复杂度,提升了频繁项和关联关系的挖掘效率。
(3)Marc算法在挖掘效率、消耗内存方面都优于Apriori、FP-Growth和Eclat算法,生成的频繁项和关联关系更加贴近样本和应用实际,且纬度越高优势越明显,更加适用于海量高维数据挖掘。
(4)Marc算法挖掘的频繁项和关联规则关系的精度为100%。
(5)在高维数据挖掘时FP-Growth和Eclat算法的挖掘效率低于Apriori。
目前分布系数是通过SigMoid函数对样本的标准差或方差进行规划所得到的,删除系数则是由根据样本均值E与分布系统相乘所得。根据标准差和方差的定义,当样本数据分布较为集中时,方差和标准差较小,经SigMoid函数规划后分布系数接近于0,删除系数也接近于0,数据降维效果差;反之,当数据较为离散时,方差和标准差较大,分布系数接近于1,删除系数接近于E,数据降维过多,造成部分关联规则丢失,不利于关联规则的挖掘,因此如何寻找合适的样本分布指标和规划函数计算分布系数是我们下一步将要研究的工作。
