基于SSA-RBF的灌区流量预测

2023-03-15单无牵宁芊陈炳才周新志罗强

科学技术与工程 2023年3期

单无牵，宁芊，*，陈炳才，周新志，罗强

(1.四川大学电子信息学院，成都 610065；2.新疆师范大学计算机科学技术学院,乌鲁木齐 830054；3.成都万江港利科技股份有限公司，成都 610064)

目前工程上对灌区流量的测量方法大部分才用的是传统的测量方法[1]，例如流速-面积法[2]、水位流量关系法[3]、堰槽法[4]等。这些传统的测量方法虽然能对灌区流量进行测量，但都存在着一些缺陷。堰槽法实施的工程成本比较高，且精度受到很多因素的影响；水位流量关系法研究的是水位与流量的内在联系，这种方法精度太差且不适用于所有的灌区；流速-面积法需要测量大量测点的流速，测量耗费时间长。

传统测流方法存在局限性能自然有相关学者进行研究，研究的方法集中于计算流体力学(computational fluid dynamics,CFD)[5]、机器学习[6-7]、流速分布规律[8-9]等。例如，Lin等[10]使用大尺度粒子图像技术测量河流表面流速结合机器学习实现了流量的非接触式测量，然而实际测量时容易仪器容易受到风速、降雨等客观因素的干扰，影响流速的测量结果导致流量估算值与真实值存在较大差距。黄靖轩等[8]对河道的流速分布规律进行研究，但研究，需要大量分布均匀且有规律的水文数据进行理论支撑，实际测量过程中测量成本较高，难以满足研究所需条件。Das 等[11]使用摩擦系数、水力半径、河床坡度等作为神经网络的输入条件对河流流量进行预测，并取得了较好的结果，但其模型的输入参数在实际过程中不易测量，且受现场测量环境的影响，参数测量的准确性并不能有效保障，影响流量预测结果。Gholami等[12-14]采用自适应神经模糊推理系统(adaptive network-based fuzzy inference system,ANFIS)研究了90°急弯的流量。提出了一种基于多层感知器(multila-yer perceptron,MLP)类型的人工神经网络模型，用于广泛预测不同的流动变量。然而其研究对象是实验室搭建简易水槽模型，实验条件过于理想化，研究成果是否适用实际的工程场景还有待验证。Chen 等[15]使用人工神经网络和支持向量机两种机器学习模型对齿形迷宫通道流量进行预测，并取得了较好的结果，但其使用的神经网络模型在训练过程中存在诸如收敛速度慢、容易陷入局部最优解、过拟合等缺陷。这些缺陷会在一定程度上影响预测的结果。

当前神经网络模型在对灌区流量进行预测中存在诸如数据来源不完整、参数测定不准确、实例验证不全面、预测结果不理想等缺陷。为了更好地提高灌区流量预测的准确性，解决水资源合理分配、调度等问题并提高神经网络模型的鲁棒性。现提出一种基于麻雀搜索算法[16](sparrow search algorithm,SSA)优化径向基(radial basis function,RBF)神经网络基函数的中心和宽度的方法。首先创建简单的RBF神经网络流量预测模型，并说明其缺陷，并在此基础上创新性地使用SSA优化RBF模型，以都江堰人民渠渠首站点27种不同水力条件下的实测数据对流量预测模型进行验证。通过对灌区流量的科学准确预测，优化目前流量测算手段，从而为灌区流量合理分配提供有效依据。

1 研究区域概况

1.1 基本情况

四川省都江堰灌区的人民渠一处属于平原灌区，灌区内干渠、分干渠共计13条，总长478.9 km，支渠60条，是都江堰灌区的重要组成部分，主要灌溉成都、德阳两市10县(市、区)242.29万亩农田，向多家重点工业企业供水和对丘陵灌区的德阳、绵阳、遂宁三市230多万亩灌面囤蓄输水及灌区城镇生活用水供水，所辖灌区由人民渠一至四期工程、蒲阳河——青白江和前进渠3个渠系组成，控灌面积达2 563 km2。

1.2 灌区流量测量现状及问题

目前人民渠渠首测站流量测算主要采用流速-面积法。测量时，在渠首平直渠段选择间距适当的两个过水断面作为测量断面，总共布置了7根测线，将梯形断面分为了8个子区域。每根测线上均使用流速仪测量若干测点流速并计算每根测线的平均速度。由于测点众多，完成一次明渠流量测量起码需要花费数小时，流量测量时间成本较高。

1.3 实测数据

本文中实测数据来源于都江堰灌区人民渠渠首站点，渠道的物理信息和水位部分信息汇总于表1。其中流量测量采用流速-面积法[2]进行测量。测量的示意图如图1所示，测量时总共布置了7根测线，每根测线的测点个数由渠道水深决定。根据渠道水位的不同，分别采用一点法、两点法、三点法。当水深处在2.16～3.3 m时，采用三点法进行测量即按y/H=0.2、0.6、0.8布置测点(y为测点高度，H为水深)；当水深处在1.6～2.15 m时，采用两点法进行测量即在y/H=0.2、0.8布置测点；当水深处在0.5～1.5 m时，采用一点法进行测量即在y/H=0.6布置测点。收集到人民渠渠首站点在27种不同水位下的水文资料。其中采用三点法测量11种水位，得到231组测点流速；两点法测量5种水位，得到70组测点流速；一点法测量11种水位，得到77组测点流速。综上得到人民渠渠首站点在27种水位下共计378组测点流速。

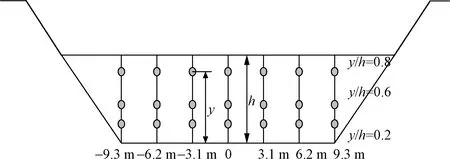
图1 测流数据示意图Fig.1 Schematic diagram of flow measurement data

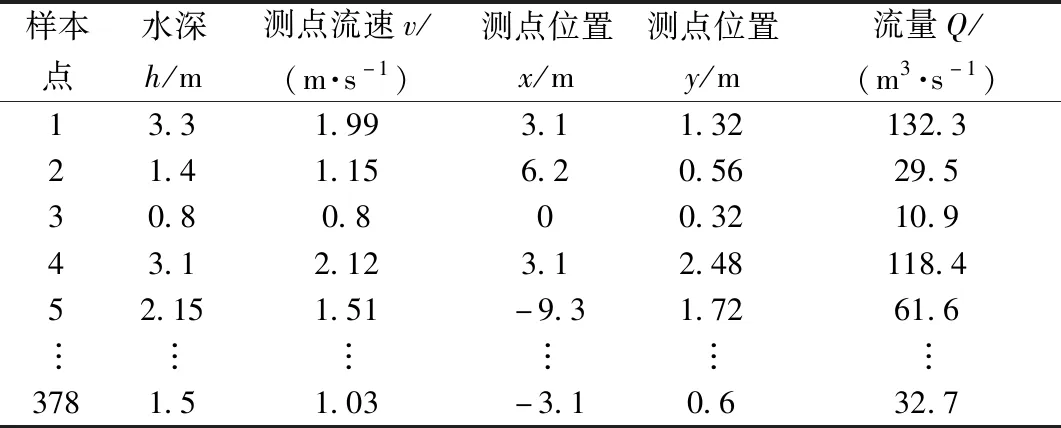
表1 部分样本数据Table 1 Partial sample data

2 流量预测模型构建

2.1 ELM神经网络

极限学习机(extreme learning machine,ELM)是一种单隐层前馈神经网络算法，由输入层、隐藏层、输出层三层组成，每层之间利用对应的映射函数来完成连接。与传统的前馈神经网络模型相比，ELM在训练过程中，隐藏层的权值和其神经元的阈值是随机产生的，无需手动赋值和更新，学习过程仅计算输出层权值，当计算求出输出层权值即完成训练。由文献[17]可知影响灌区流量测量的主要因素为测点参数以及渠道参数，故以渠道水深H、测点流速v、测点位置x、y为ELM的4个输入因子，以流量Q为输出因子，ELM的结构图如图2所示。

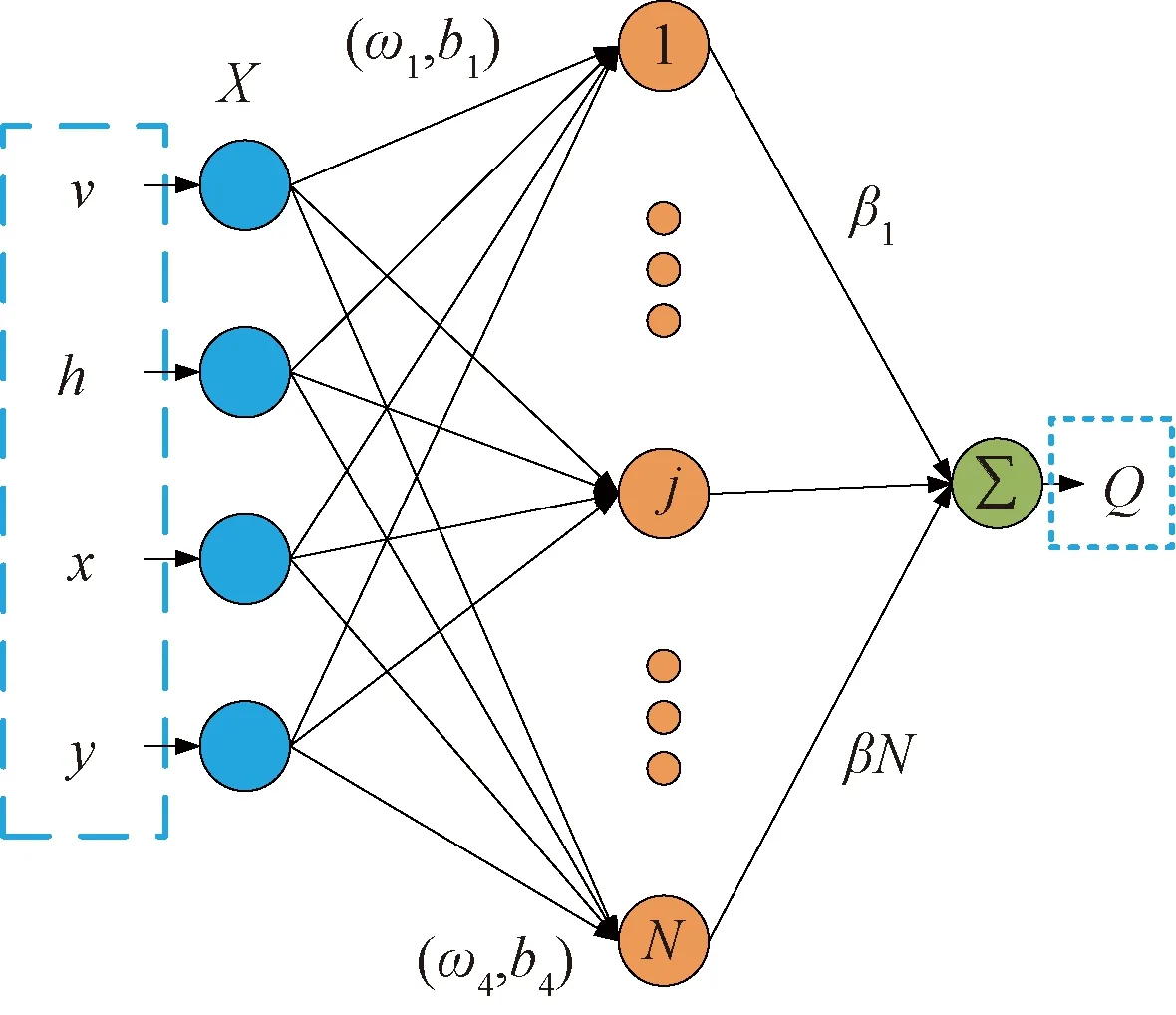
图2 基于ELM神经网络的灌区流量预测模型Fig.2 Irrigation district flow prediction model based on ELM neural network

假设有N个样本(Xi,Qi)，其中Xi=[x1,x2,x3,x4]T表示模型的输入参数。x1、x2、x3、x4分别代表渠道水深h、测点流速v、测点位置x、y。Q为流量预测值。综上，ELM模型预测灌区流量的输出可表示为

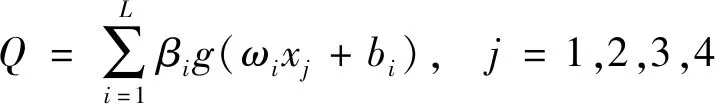
(1)

式(1)中：L为隐藏层神经元个数；g(x)为激活函数；ωi为输入层到隐藏层的调度权值；bi为第i个隐层单元的阈值；βi为输出权值。

2.2 RBF神经网络

神经网络由多个神经元以及层级相互连接组成的拓扑结构，其优点在于能够通过大量数据的训练完成输入与输出之间的非线性映射，训练完成后，每当有新的数据输入便能输出一个较为可靠的结果。RBF神经网络由于其简单、灵活等特点常用于解决各种水利工程问题。RBF神经网络通常由输入层、隐藏层、输出层3层组成，每一层均包含若干神经元。渠道水深h、测点流速v、测点位置x、y为RBF的4个输入因子，流量Q为输出因子，建立的神经网络模型如图3所示。

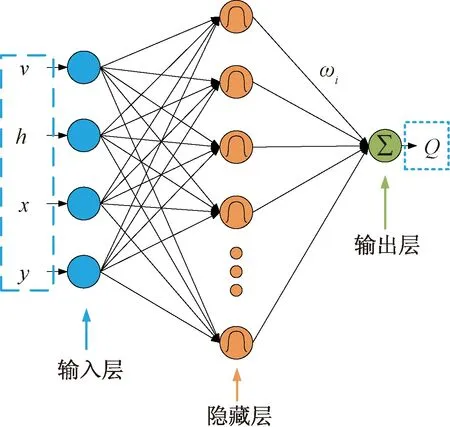
图3 基于RBF神经网络的灌区流量预测模型Fig.3 Irrigation district flow prediction model based on RBF neural network

由于隐藏层的激活函数选择的是高斯函数，输出层采用线性变换，故输入与输出之间的关系为

(2)

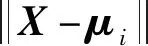
2.3 麻雀搜索算法

麻雀搜索算法(SSA)[16]是一种通过模拟麻雀的觅食和反捕食行为来进行局部和全局搜索的优化算法。麻雀搜索算法将麻雀分为发现者和加入者两类，其基本原理是：发现者负责找寻食物丰富并为加入者提供觅食方向，加入者通过发现者来获取食物，同时加入者会不断监控发现者并抢夺食物以保障自己的捕食率。当麻雀种群受到捕食者攻击时，发现者将发出预警信号，若超出阈值将带领加入者撤退到安全区域。这个过程中发现者和加入者的身份是动态变化的，每一只麻雀都可能随时转换身份。

模拟实验中，由n只麻雀组成的种群为

(3)

式(3)中：d为待优化问题的维数；n为麻雀的数量。

麻雀种群适应度的形式为

(4)

式(4)中：f表示适应度值。

发现者的位置更新公式为

(5)

式(5)中：t表示当前迭代次数；T表示最大迭代次数；Xi,j(t)表示第i只麻雀在第j维迭代次数为t时的位置信息；α为[0,1]的随机数；R(R∈[0,1])表示预警值；ST(ST∈[0.5,1])表示安全值；Q为服从正态分布的随机数；L表示一个1×d的矩阵，其内部每个元素都为1。

加入者的位置更新公式为

Xi,j(t+1)=

(6)

式(6)中：Xp(t+1)是当前发现者中适应度最优的位置；Xworst(t)是当前全局适应度最差的位置；A+=AT(AAT)-1,A表示一个与麻雀个体同维度的列向量，内部元素由1与-1随机组成。

侦察者的位置更新公式为

Xi,j(t+1)=

(7)

式(7)中：Xbest(t)为当前的全局最优位置；β为步长控制参数，为服从均值为0、方差为1的正态分布的随机数；K∈[-1,1]是一个随机数；fi则为当前麻雀个体的适应度；fg和fw分别为当前全局最佳和最差的适应度值；ε为较小的常数。

2.4 SSA优化RBF模型

传统的RBF神经网络中，由于隐藏层节点的基函数中心和宽度是随机产生的，如果使用传统的RBF神经网络在预测灌区流量模型可能会导致无法得到最优解，从而不断增加隐藏层神经元个数使得网络结构变的复杂。针对上述问题，现使用SSA优化RBF神经网络的中隐藏层的基函数中心和宽度，从而获取最优的参数。

使用SSA优化RBF时，选取训练集与测试集的均方误差作为种群的适应度。首先读取表1中的样本集，按照7∶3的比例将样本集分为训练集(70%)和测试集(30%)，并将数据归一化处理；其次确定模型的输入输出，初始化基函数中心和宽度、隐藏层到输出层之间的权值，种群的大小，发现者加入者之间的比例等；使用SSA优化基函数中心和宽度，并将最后优化的结果赋给RBF完成模型的训练。SSA-RBF的灌区流量预测流程图如图4所示。

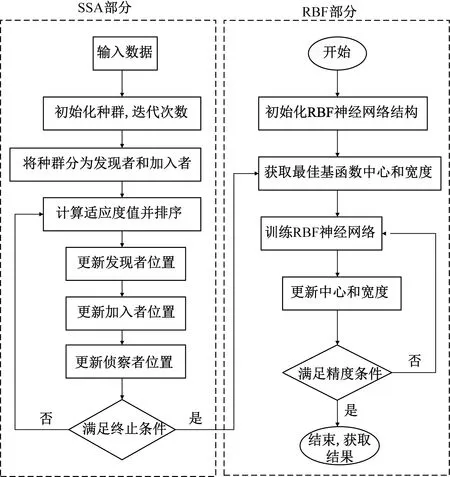
图4 SSA优化RBF神经网络流程图Fig.4 Flow chart of SSA optimization of RBF neural network

3 结果和讨论

3.1 评价指标

对ELM、RBF、SSA-RBF 3种测流模型进行研究，并得到了测流结果，然而单一的对比无法说明模型的好坏，故采用确定系数R2、均方根误差(root mean square error,RMSE)、平均绝对误差(mean absolute error,MAE)、残差质量系数(coefficient of residual mass,CRM)4种评价指标来进行。R2越接近1模型性能越好，RMSE、MAE、CRM越接近于0，模型性能越好,这些指标的计算公式为

(8)

(9)

(10)

(11)

式中:QPi是预测的流量，m3/s；QMi是实际测量的流量，m3/s；n为参与计算的流量个数。

3.2 灌区流量预测结果

以都江堰人民渠渠首站点的378组实测数据对SSA-RBF模型进行研究，其中265组(70%)数据作为训练样本，113组(30%)数据作为测试样本。单一的结果无法说明模型的好坏，故以同样的输入并分别得出ELM、RBF、SSA-RBF模型预测的流量。通过预测流量与真实流量对比以及四种评价指标来详细评估模型在预测灌区流量方面的性能。结果记录在图5～图8以及表2、表3中。其中图5～图7为3种模型流量预测结果；图8为预测结果与对应真实值之间的偏差；表2为流量预测结果偏差分布对比；表3为误差评价指标的结果。

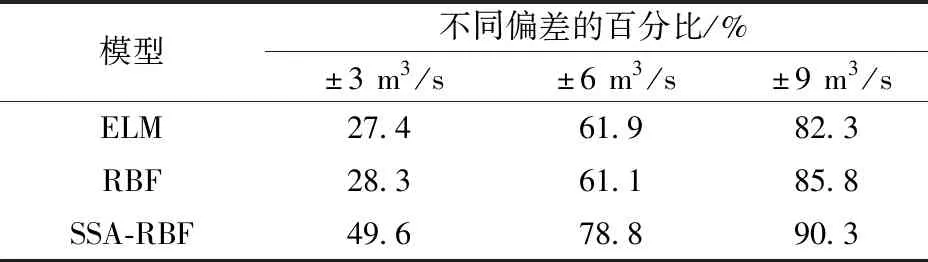
表2 流量预测结果偏差分布对比Table 2 Comparison of error distribution of flow prediction results

表3 误差评价指标结果Table 3 Error evaluation index results

由图5～图8可以看出，ELM、RBF、SSA-RBF 3种模型均能对灌区流量进行有效预测。而SSA-RBF模型与其他2种模型相比，流量的预测结果更加接近真实值，误差分布也更加均匀。

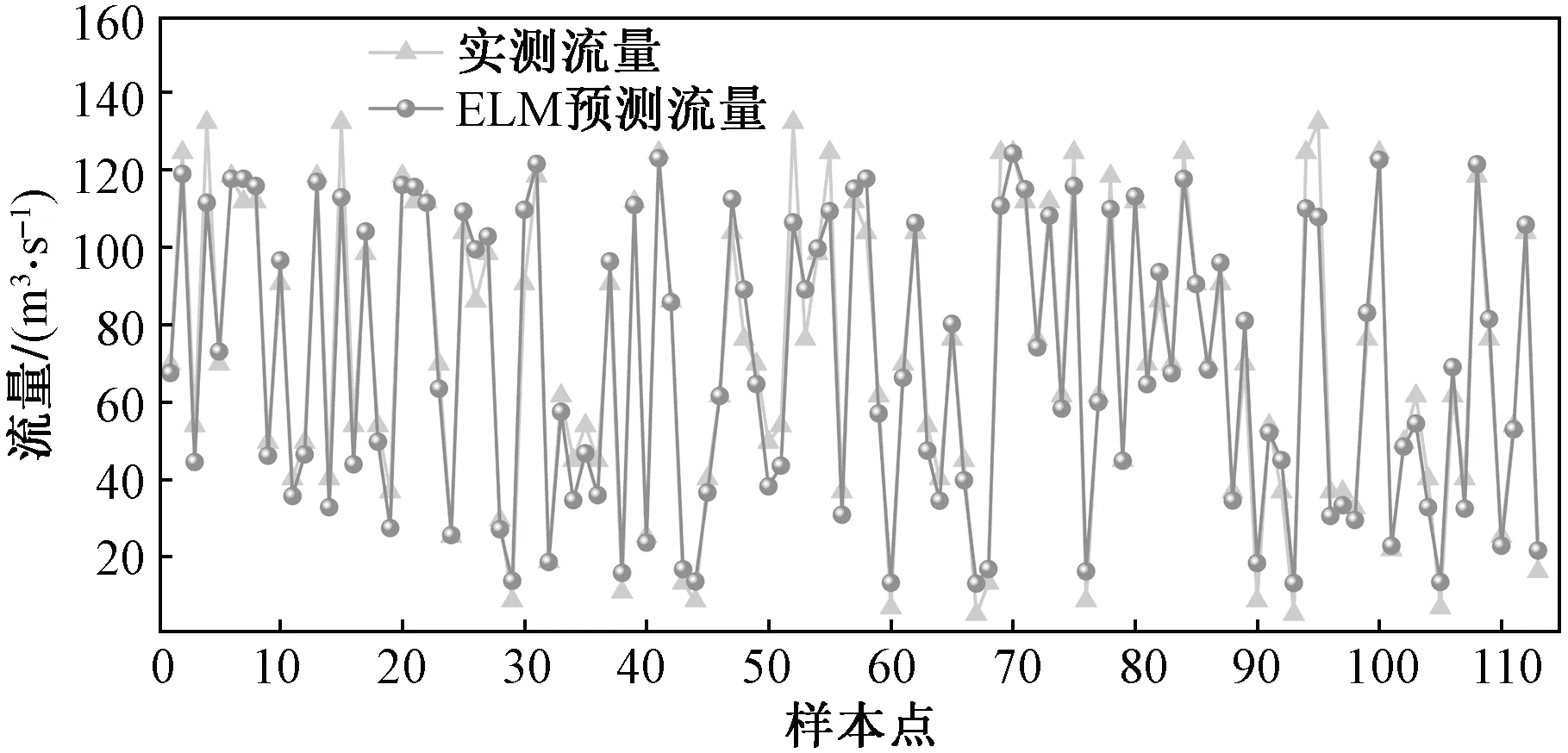
图5 ELM模型预测结果Fig.5 Prediction results of ELM model

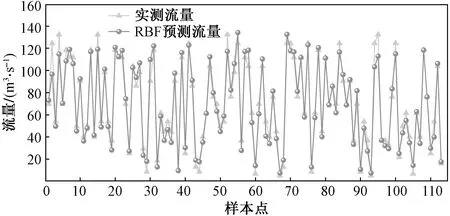
图6 RBF模型预测结果Fig.6 Prediction results of RBF model

图7 SSA-RBF模型预测结果Fig.7 Prediction results of SSA-RBF model

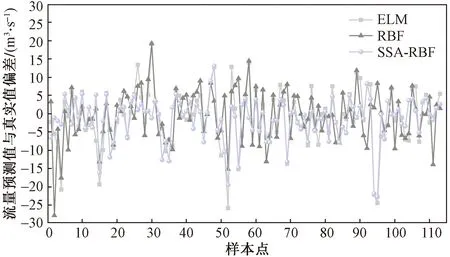
图8 模型预测结果和真实值偏差Fig.8 Deviation between model prediction results and real values

由表2、表3可以看出ELM与RBF预测差异较小，而使用SSA优化RBF神经网络预测流量偏差在±3 m3/s的百分比提高21.3%，偏差±6 m3/s的百分比提高17.7%，偏差在±9 m3/s的百分比提高4.5%。使用SSA优化RBF神经网络后R2提高0.024、RMSE减少2.192、MAE减少1.829、CRM减少0.009 3。

最终可以得出结论SSA-RBF模型预测效果更好，使用SSA优化RBF神经网络是有效的。