浅覆土盾构穿越潮汐河流地层变形规律

李兴杰，路冬冬，孙海宾，胡家乐，李建立，吴雄，许江波*

(1.中铁二十四局集团有限公司,上海 200433；2.长安大学公路学院,西安 710046)

近年来，中国交通运输发展取得了举世瞩目的成就。除了地面交通网络建设，城市地下空间开发利用同样大有可为[1]，截至2021年年底，中国大陆地区(不含港澳台)共有50个城市开通城市轨道交通运营线路283条，运营线路总长度9 206.8 km。其中，地铁运营线路7 209.7 km，占比78.3%[2]。城市地铁建设技术日渐成熟，但面对复杂的水文地质情况，仍有诸多工程难题亟需解决，浅覆土盾构穿越潮汐河流就是其中较为复杂的工程问题之一。浅覆土盾构穿越河流，需保证河底地层的安全稳定性。若地层变形过大，势必会产生裂缝，发生冒顶和河水倒灌隧道的现象，由此可见对河底地层的变形研究极为重要。

国内外众多学者对盾构法施工的下穿河流进行了详细研究。李振东[3]和丛恩伟[4]分别依托北京地铁盾构下穿昆玉河、通惠河的工程施工，研究了最优的施工参数及注浆压力以控制地表沉降。闫潇等[5]依托太原地铁下穿迎泽湖工程，提出调整渣土改良参数,优化同步注浆配比,对盾构机尾刷改造等措施以降低施工风险。韩磊等[6]以江阴市澄江西路公路隧道下穿闸桥河及锡澄运河为背景工程，根据隧道穿越地层的工程地质条件和浅覆土段盾构施工风险，提出了相应的河底加固及施工控制措施。李明华等[7]依托南昌地铁1号线下穿抚河工程实际，提出了有效的施工控制措施。

张志华等[8]以武汉地铁7号线大直径越江隧道段为工程背景,建立了大直径浅埋隧道盾构掘进室内缩尺试验模型，同时建立了同尺寸的浅埋隧道盾构掘进离散元模型,对盾构掘进过程中地表沉降、开挖面前方土层中颗粒配位数以及黏结破裂区域进行了分析研究，并与室内试验结果进行了对比分析。梁孝等[9]以杭州地铁5号线盾构施工工程为背景，通过数值模拟为风险评价提供沉降数据样本。通过模糊综合评价和反向神经网络方法进行计算，确定风险指标变形值与风险因素的对应关系，进行风险评价分析。杜远港等[10]采用数据统计分析、相关性分析和周期性分析方法，仅基于监测数据对潮位变化引起的上海某越江盾构隧道变形的影响规律进行研究。胡长明等[11]以成都地铁3号线盾构隧道穿越沙河工程为背景，利用ABAQUS模拟不同保护措施下的土层反应，结合实际施工数据，研究盾构隧道临近河流始发并穿越的有效掘进技术。冯晓九等[12]结合常州地铁二号线一期工程实际，运用ABSQUS对盾构下穿河流施工沉降进行数值模拟分析,研究盾构法在富水粉砂地层中穿越河流减小沉降的方法。李自力等[13]依托常州地铁二号线下穿越京杭运河区段工程，通过利用MIDAS/GTS NX进行数值模拟，分析了注浆压力及注浆量对地表沉降的影响。毕景佩等[14]用MIDAS/GTS有限元软件假定实际地层均质水平地层，建立了数值模型对盾构区间近距离下穿小月河桥工程中桥面、盖梁及桥桩位移变化规律特征进行有限元分析。王金安等[15]以南京地铁越江盾构隧道工程为依托，假定地层均质水平使用有限差分软件FLAC3D对工程施工各个阶段进行了计算分析,研究了河底的沉降规律。高永涛等[16]以苏州地铁6号线双线盾构隧道下穿外城河为背景，同样假定地层水平，借助MIDAS数值模拟与现场监测数据重点讨论了盾构施工中注浆压力和注浆材料对地表变形的影响。

综上所述，目前关于盾构下穿河流的研究取得了丰硕的成果，就研究内容而言涉及施工前的风险评价分析，施工过程中的施工参数、注浆压力、工作面压力、渣土改良参数、同步注浆配比以及盾构机尾刷等对地表沉降的影响以及施工后的加固效果评价；就研究方法而言，主要是单一或综合运用模型试验、数值模拟和现场监测数据开展研究。然而数值模拟时，为降低模型建立的难度，常将实际的起伏地层简化为水平地层，从而导致数值模拟效果与工程实际有一定偏差，故建立与实际相符的起伏地层对提高数值模拟的准确度意义重大；就工程地域而言，大多是依托水位不变的内陆河流进行分析，鲜有关于盾构下穿水位周期性变化的潮汐河流的分析与讨论，开展盾构下穿潮汐河流的地层变化规律研究对于指导沿海地区地铁建造有一定的指导意义。因此，依托青岛地铁浅覆土盾构穿越潮汐河流工程，基于浅覆土盾构穿越潮汐河流工程实际问题，重点考虑河流水位的潮汐变化，结合工程中采用的注浆压力、工作面压力等施工参数，建立更加贴近实际的起伏地层模型，开展数值模拟，进而对地层变形规律开展研究。

1 数值模型建立

1.1 工程概况

依托青岛地铁四号线沙崂区间工程实例，盾构法隧道斜穿潮汐河流约101 m，现场实际穿越情况如图1所示。河底处隧道埋深约7 m，属于浅覆土隧道。施工前河底为自然河床，未经硬化处理，且线路下穿河流处靠近沙子口湾，距离入海口约 500 m，海水涨潮时水深约2 m，海水会倒灌进河道内，进而影响到线路周围地下水环境；河流的地层情况如图2所示，由上而下依次为素填土、细砂、粉质粘土、粗砾砂、强风化带、中风化带、微风化带。洞身范围内主要为粗砾砂。盾构掘进至河底时，可能会因为河底至隧道洞顶土层覆盖较薄7 m，出现河水下渗，甚至河水从隧道突涌而出的情况，风险等级I级。

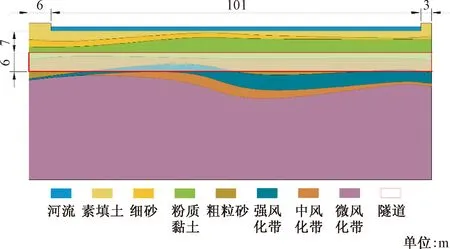
图2 地层分布剖面图Fig.2 Profile of stratigraphic distribution

1.2 计算模型建立

运用Rhino软件按照起伏地层的实际情况建立模型并划分网格后导入FLAC3D软件，土体和岩层均采用Mohr-Coulomb模型，注浆层采用弹性模型。盾构隧道直径为6.0 m，两隧道间水平间距为24 m，为消除边界效应，模型尺寸设置为长×宽×高=110 m×70 m×50 m，为方便模型建立和计算，预先在建立模型阶段划分开挖区域并分组，具体模型建立如图3所示。

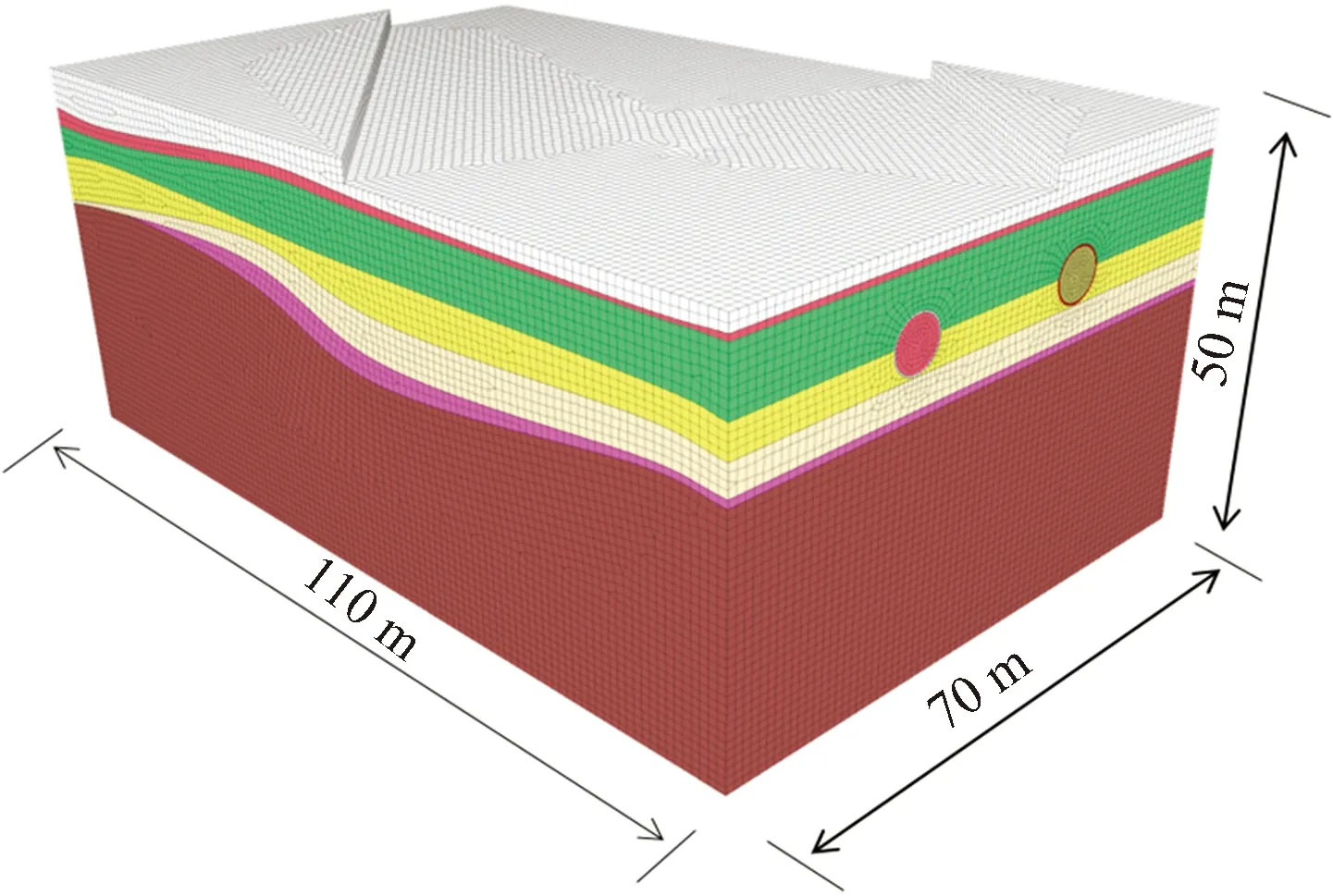
图3 数值计算模型Fig.3 Numerical calculation model

1.3 材料物理力学参数

计算模型采用的岩土物理力学参数依据实际工程的详细勘察报告选取。开挖范围内土层的各物理力学参数采用加权平均值，权重为各土层厚度。具体选用的各岩土物理力学参数如表1所示。

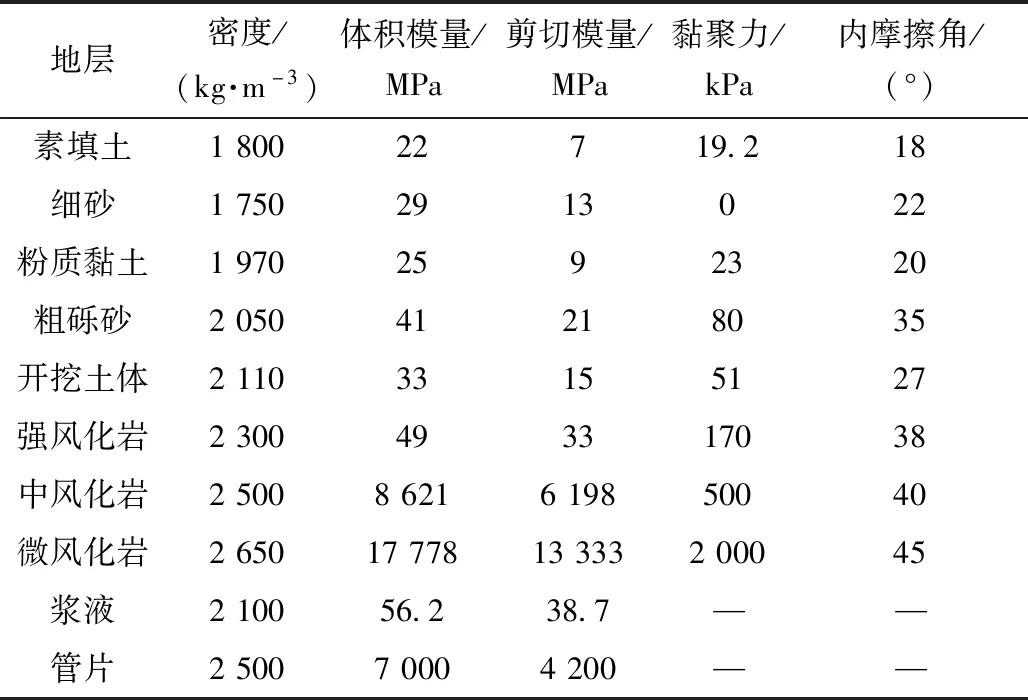
表1 岩土物理力学参数Table 1 Physical mechanics parameter of rock and soil

1.4 工况模拟

现场施工中，右线隧道先行开挖，随后进行左线隧道开挖。左线隧道到达河岸进行穿河施工时，距右线开挖面290环，两台盾构机前后距离435 m。

为分析盾构开挖和潮汐河流对地层变形的影响，数值模拟选取潮汐作用时河道水位变化的代表性深度0、0.5、1.0、1.5、2.0 m共计五种工况进行。在施工前已对河道进行防渗处理，因此可不考虑渗流作用，将河道水位随潮汐的涨落以不同的均布荷载施加于河道底面后进行模拟。每步开挖长度为1.5 m，与实际施工保持一致。模拟过程记录沿隧道轴线和垂直于隧道轴线方向上的共计200余个监测点数据并开展分析。

2 模型计算分析

五种工况下，右线隧道开挖20环时，垂直于右线隧道轴线方向的地层竖向位移如图4所示，不同工况下盾构开挖均会引起隧道上部地层发生沉降，沉降最大点都出现在洞顶位置，地层的变形规律类似。五种工况的不同之处在于，拱顶的沉降量随水深的增加而增加，水深为0时，拱顶沉降为16.47 mm，当水深增加到2.0 m时，拱顶沉降达到17.65 mm。不同水深下盾构施工所引起的地表沉降范围有所区别，沉降槽的形状及地表沉降量均有差异。

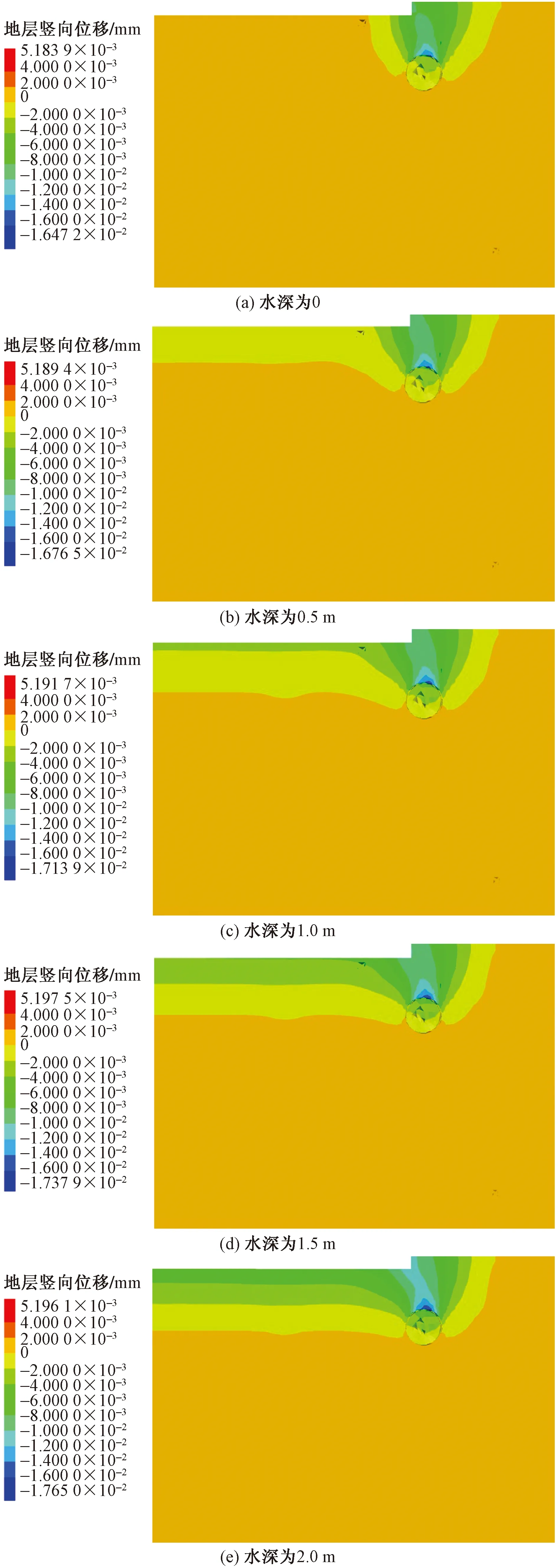
图4 开挖20环垂直于隧道轴线地层竖向位移云图Fig.4 Vertical displacement nephogram of stratum perpendicular to tunnel axis when excavating 20 rings

开挖进尺为20环时，选取距洞口30 m的横截面为监测面，对监测面上地表各点的沉降进行对比，如图5所示。水深为0时，横截面上沉降曲线呈抛物线并沿隧道中心线成轴对称。水深0.5、1.0、1.5、2.0 m时，沉降曲线形状仍接近于抛物线，但并不对称。沉降槽宽度均为6D(D为隧道直径)左右。隧道开挖对隧道右侧15 m(即2.5D)范围内的土体产生扰动，且扰动范围受水深的影响不大。在隧道右侧6 m(即1D)时，水深对周围土体沉降的影响开始出现差异化，并且差异随着距离的增加愈加明显。同一水深下，40 m以后的沉降基本一致，沉降随水深的增加而增大，建立40 m处的沉降值与水深的关系，如图6所示。分析发现地层沉降与水深呈明显的正比例关系，即y=3.08x。

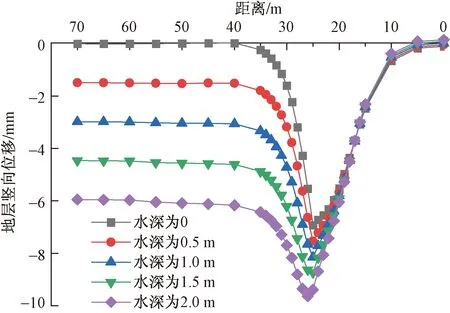
图5 不同工况下第20环横截面地层竖向位移图Fig.5 Vertical displacement map of the 20th ring cross section under different working conditions

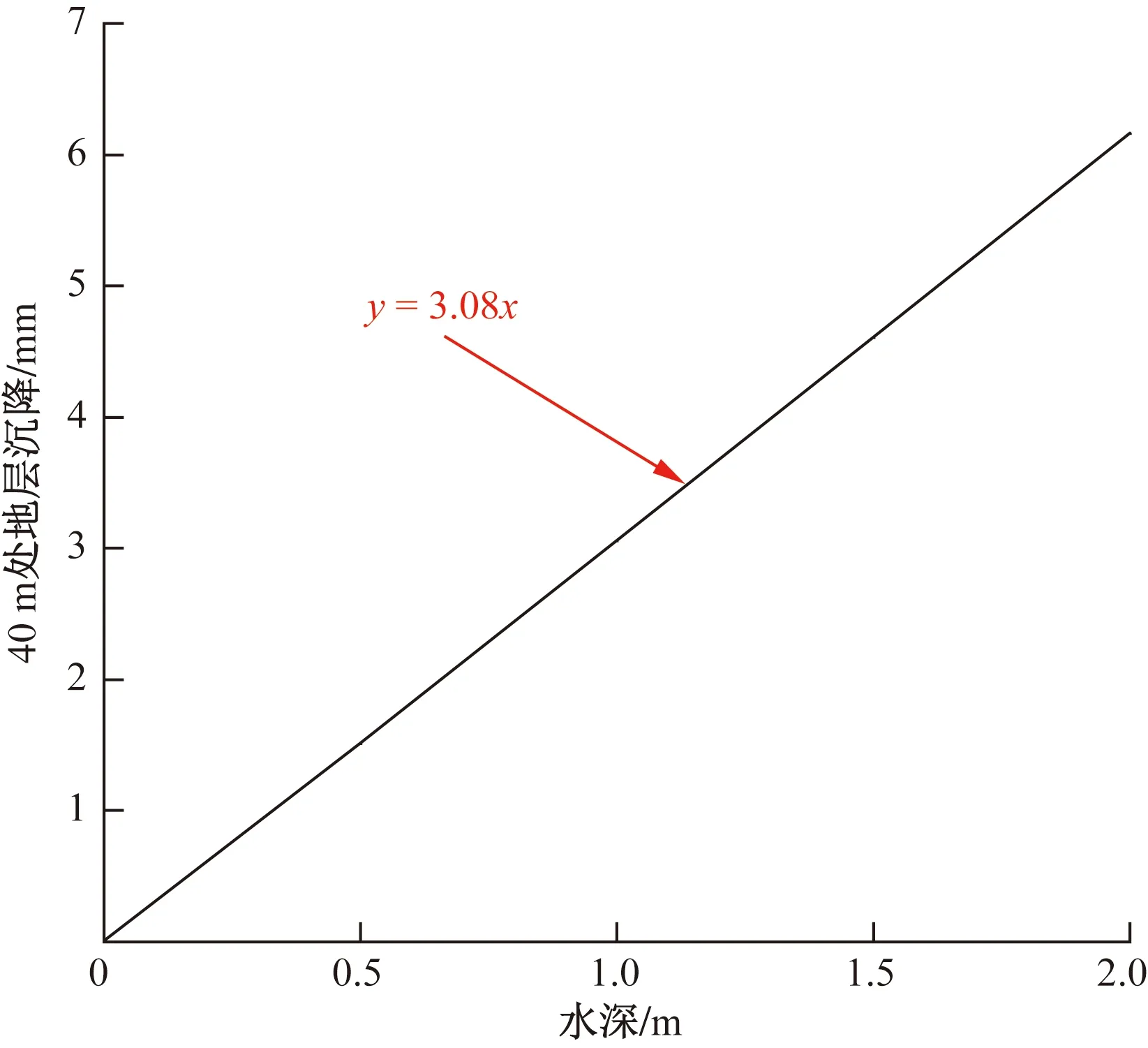
图6 第20环时40 m处的沉降值与水深的关系Fig.6 Relationship between settlement at 40 m and water depth at 20th ring

右线隧道穿河工程掘进共计73环，109.5 m。盾构掘进过程中，不同开挖进尺对应的监测面上地表各点的横向沉降曲线如图7所示。从图7中可以看出，水深为0时，随着开挖的进行，沉降曲线由水平线逐渐下凹转化为抛物线，在水深0.5、1.0、1.5、2.0 m时，沉降曲线由“Z”形曲线下凹转化为“√”形，曲线顶点位移隧道中心线上，左侧拐点距隧道中心线9 m(1.5D)。开挖到第12环左右时，截面开始受到扰动，产生因开挖引起的沉降，到第30环左右，沉降基本稳定。水深从0～2 m，最大沉降量依次为23.695、24.161、24.735、25.384、26.160 mm。

图7 不同进尺下距洞口30 m横向沉降曲线Fig.7 The lateral settlement curve of 30 meters away from the hole under different footages

对右线隧道轴线上距洞口30 m(第20环)处的地表沉降进行单独分析，绘制沉降时序图如图8所示，盾构掘进到第12环时，此处地层开始产生较小变形，随着盾构掘进，变形量逐渐增大，在盾构掘进到第20环，即到达该点时变形速率明显加快，具体表现为图中曲线斜率的增大，该变形速率保持不变直至盾构通过10环后减小。在盾构掘进至45 m(30环)时，30 m(20环)处的地层变形基本稳定。不同水深下的曲线整体形态一致，仅在最终沉降上有细微差异，此处差异较小的原因分析有二，其一为盾构施工对地层的扰动，随着距拱顶的距离的增大而逐渐减弱。在地表处，盾构施工扰动造成的影响最小，故不同水位引起的地表沉降差异较小；其二为30 m处距离岸边较近，故河流水位对此位置的影响相较于河道中央较小。

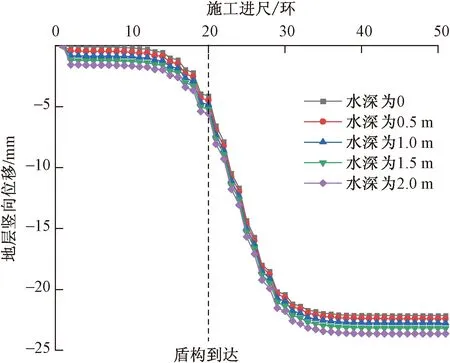
图8 右线隧道30 m处上方地表沉降时序图Fig.8 Time series diagram of surface settlement above 30 m right tunnel

在五种工况下，右线隧道开挖至60环时，沿右线隧道轴线方向的地层竖向位移如图9所示，不同水深下的盾构开挖会造成隧道顶部地层沉降，底部地层隆起，且隆起区域主要在开挖面至其后40 m范围内。最大沉降出现在洞口区域，最大隆起出现盾构工作面后20 m附近，最大隆起量随河道水位深度的增加而减小。由图9可见，水深为0时，开挖面前的沉降区仅存在于开挖面前方10 m范围内的土体，随着水深增加，沉降区的范围逐渐增大。

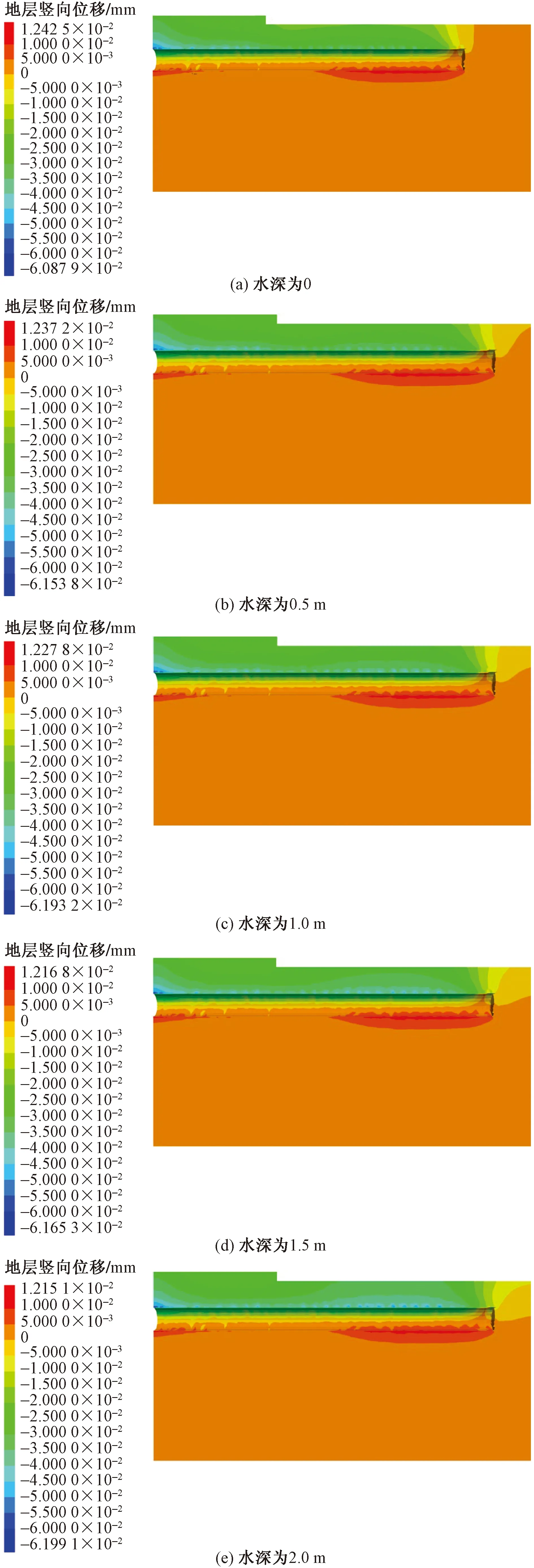
图9 开挖60环时隧道轴线地层竖向位移云图Fig.9 Vertical displacement nephogram of tunnel axis stratum during excavation of 60 rings

取五种工况下，右线隧道开挖至60环时，沿右线隧道轴线方向地表的竖向位移如图10所示。不同水深对应的曲线整体形态一致，而沉降量有所差别。水深2.0 m的最终沉降量比水深为0最终沉降量多50%。隧道掘进在时间效应上的地表沉降分为4个阶段：先期未扰动阶段、初期沉降阶段、中期盾构开挖及加固阶段、末期固结沉降阶段。对于本工况而言，70 m前为先期未扰动阶段，不发生沉降；70～60 m为初期沉降阶段，沉降量和变化速率小；60～50 m为中期盾构开挖及加固阶段，沉降量大，变化速率快；50 m以后为末期固结沉降阶段，沉降量变小，变化速率变慢。地层的沉降变化量与水深的不同而不同，关系如图11所示。

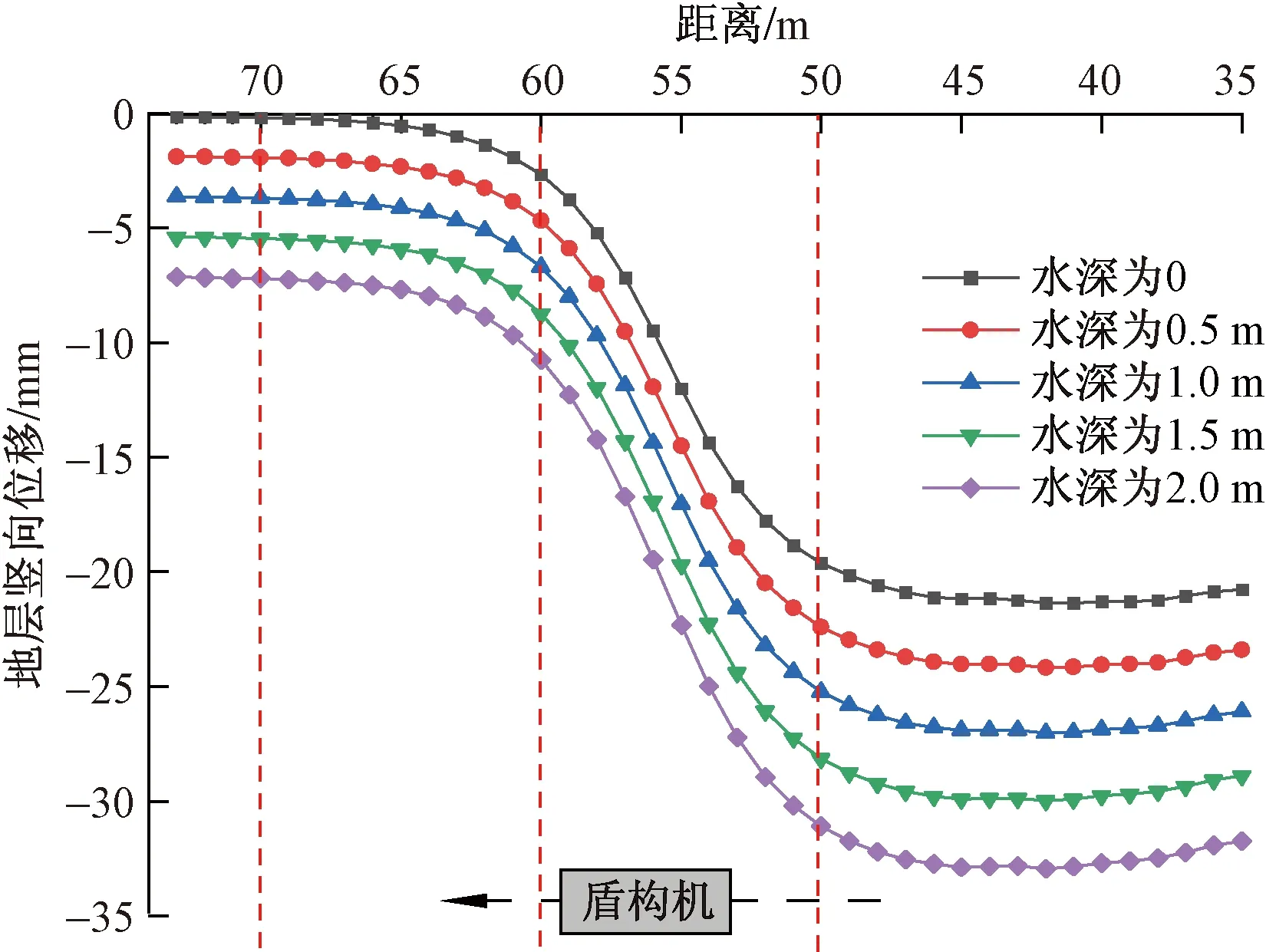
图10 开挖60环右线地层竖向位移图Fig.10 Vertical displacement map of excavation 60 ring right line

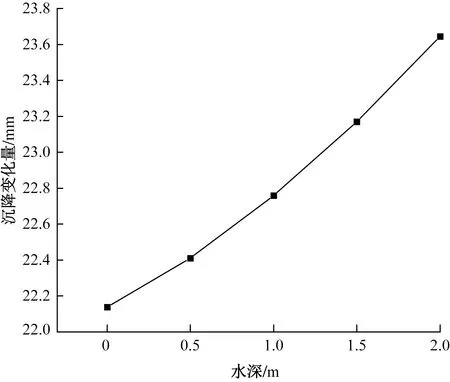
图11 地层沉降变化量与水深关系图Fig.11 The relationship chart between the variation of stratum settlement and water depth

3 讨论

盾构开挖引起隧道底部隆起呈圆弧状隆起。通常来说，造成隧道底部隆起的原因有：岩层的矿物成分、岩体结构特征以及工程偏应力。本研究中的隧道穿越土层为粉质黏土层和砂土层。粉质黏土中含有高岭石、伊利石、蒙脱石等遇水膨胀的矿物成分，但其位于隧道上半部分，即使其遇水膨胀，也并不会引起隧道底部隆起，而隧道底部所在地层为砂岩，不含膨胀型矿物成分。隧道所在的两地层均不含断层、节理等岩体结构，故排除前两种引起隧道底部隆起的原因。本工程中隧道底部隆起的绝大部分原因是隧道开挖导致的工程偏应力，其引起砂土层应力释放，砂土层扩容膨胀，最终表现为隧道底部隆起。

盾构掘进过程中隧道上部地层沉降原因之一是地层受扰动。盾构掘进必然会对土体产生扰动，打破土层原来的应力平衡状态，土体的初始应力释放，应力重新分布。土体发生变形进而达到新的应力平衡状态。隧道上部地层沉降的原因之二为地层损失。盾构施工开挖土体，若实际排土量大于理论排土量，则说明出现了超挖的情况，此时地层损失较大，上部土体下沉以弥补超挖的土体。在数值建模中，圆形隧道的网格划分难免出现不规则形状，在数值模拟盾构开挖时，就会造成少量超挖的现象，进而导致地表沉降。

本文中数值模拟的横向沉降槽与Peck经验公式相符，呈抛物线型，主要是因为的隧道中心位置地层损失量最大，周围土体向此处填充形成盆状沉降区，在横截面上表现为抛物线型。数值模拟结果表明，沉降槽的宽度并不受河道水位深度的影响，而河底的最终沉降量与水位深度正比例相关。因不考虑渗流作用，河道水位随潮汐作用的涨落即转化为施加于河底的均布荷载，对地层变形的影响也等同于在地层上方施加超载而引起的沉降。

隧道掘进在时间效应上的地表沉降分为4个阶段：先期未扰动阶段、初期沉降阶段、中期盾构开挖及加固阶段、末期固结沉降阶段。四个阶段的分界面为开挖面前10 m、开挖面、开挖面后10 m。先期未扰动阶段即为在此阶段盾构掘进对地表沉降的影响微乎其微；初期沉降阶段为盾构到达前，地层因受到开挖的扰动而发生小幅度缓慢沉降；中期盾构到达及加固阶段为地表沉降量大且变化快的阶段，主要因为该阶段对土体的扰动大，地层损失量大，管片脱离盾尾后的空隙需选取合理的注浆压力和浆液来填充，各参数的合理与否对地表隆沉量有极大的影响；末期固结沉降阶段沉降量小且是一个缓慢变化的过程，此阶段的沉降主要是由于土体孔隙中的水被逐渐排出，孔隙体积减小，土体变得密实。

4 结论

用数值模拟的手段，建立了起伏地层模型，对浅覆土盾构隧道穿越潮汐河流的地层变形规律进行了研究，得到了如下结论。

(1)盾构穿越潮汐河流地层的地层变形规律与盾构正常掘进的地层变形规律类似，均会引起底层的隆起与沉降。盾构隧道开挖引起隧道底部的隆起，在不含膨胀型矿物及不含岩体结构面的地层，隧道底部隆起的主导因素大多为隧道开挖产生的工程偏应力引起的土层扩容膨胀。盾构隧道开挖过程中的隧道上部土层沉降的原因主要为土层扰动和地层损失。

(2)不同河道水位深度下的横向沉降曲线不同，水位为0时，横向沉降曲线为“抛物线”型，水深0.5、1.0、1.5、2.0 m时，横向沉降曲线为“√”形，且不同水深对应的最大沉降量也有差别。

(3)地层的最终沉降量与河道水位深度正相关，水深2.0 m的最终沉降量比水深为0最终沉降量多50%。因此在浅覆土盾构穿越河道时，需注意河底沉降量，施工前按照最大河道水位深度计算河底地层沉降。预先做好加固和防渗措施，防止河底产生较大沉降一起土体开裂，进而造成河水渗漏。

(4)隧道掘进在时间效应上的地表沉降分为四个阶段：先期未扰动阶段、初期沉降阶段、中期盾构开挖及加固阶段、末期固结沉降阶段。在中期盾构开挖及加固阶段沉降量大且变化速度快，需加强该阶段的监测频率，采取有效措施控制排土量，同时需选取合理的施工参数，减小对地层的扰动，并及时采取加固措施，防止地层产生过大沉降。