基于CEEMD-LMD-SCN的集合型配电网故障选线方法

2023-03-15邓思敬吴浩杨玉萍漆梓渊邹西

科学技术与工程 2023年3期

邓思敬，吴浩，2*，杨玉萍，漆梓渊，邹西

(1.四川轻化工大学自动化与信息工程学院，自贡 643000；2.人工智能四川省重点实验室，自贡 643000)

在电力系统飞速发展的情况下，保证配电系统的平稳运行成为提升电网供电可靠性的关键环节。据统计，中低压配电网故障时多数为单相接地故障[1-2]。故障选线装置由于误选、漏选等情况，会减弱对故障线路的辨识能力。所以为了降低线路故障时对供电的影响，使得供电系统能够稳定运行，有必要对故障线路做出迅速、正确的识别。

随着配电网故障诊断技术的不断发展，人们对配电网故障选线方法进行了大量的研究和改进。目前故障选线主要使用特征故障量，如暂态分量、稳态分量、行波分量[3]和扰动量[4-5]等，数据处理的方法包括小波变换法[6-7]、S变换法[8-9]、Prony法[10]、集合经验模态分解(ensemble empirical mode decomposition，EEMD)[11]和变分模态分解(variational mode decomposition，VMD)[12]等。用于故障选线的分类网络目前主要包括支持向量机(support vector machines，SVM)[13]、极限学习机(extreme learning machine，ELM)[14]、卷积神经网络(convolutional neural networks，CNN)[15]、门控循环单元(gated recurrent unit，GRU[16]等。文献[17]利用希尔伯特-黄变换提取零序电流频域信息，将特征向量输入改进的人工免疫网络进行故障判断，该方法有一定的耐受高阻能力，但抗噪声干扰能力较差。文献[18]利用EEMD算法对暂态电流信号进行特征提取，基于主成分分析法(principal component analysis，PCA)实现对样本数据的识别，该方法在不同过渡电阻时具有优势，但EEMD分解存在重构误差大、分解完备性差等问题。文献[19]利用VMD进行信号分解，将故障特征输入到长短期记忆网络(long short term memory，LSTM)网络进行故障诊断，相比其他算法，收敛速度更快，运行时间更短，但选线的准确率较低，可靠性不高。

随着用户对供电可靠性的要求不断提高，需要建立抗噪声能力强且耐受高阻的故障选线模型，进行准确、快速的故障线路识别。鉴于此，现研究一种基于互补集合经验模态分解(complementary ensemble empirical mode decomposition，CEEMD)-局部均值分解(local mean decomposition，LMD)-随机配置网络(stochastic configuration network，SCN)的集合型故障选线方法，利用CEEMD与LMD对零序电流进行特征提取，计算出CEEMD能量熵与LMD能量熵，将CEEMD能量熵和LMD能量熵进行组合，形成包含更多故障信息的组合特征向量，利用收敛速度快且泛用性强的SCN网络对故障线路进行识别和分类。将CEEMD能量熵与LMD能量熵进行组合，改善传统单一特征输入的局限性，通过仿真实验验证了该方法具有较强的抗噪声能力且耐受高阻。

1 故障零序电流特性分析

当配电网出现故障时，分析故障电流的暂态过程[20]。线路发生接地故障时的等效图如图1所示。

当线路故障时，暂态电流表达式为

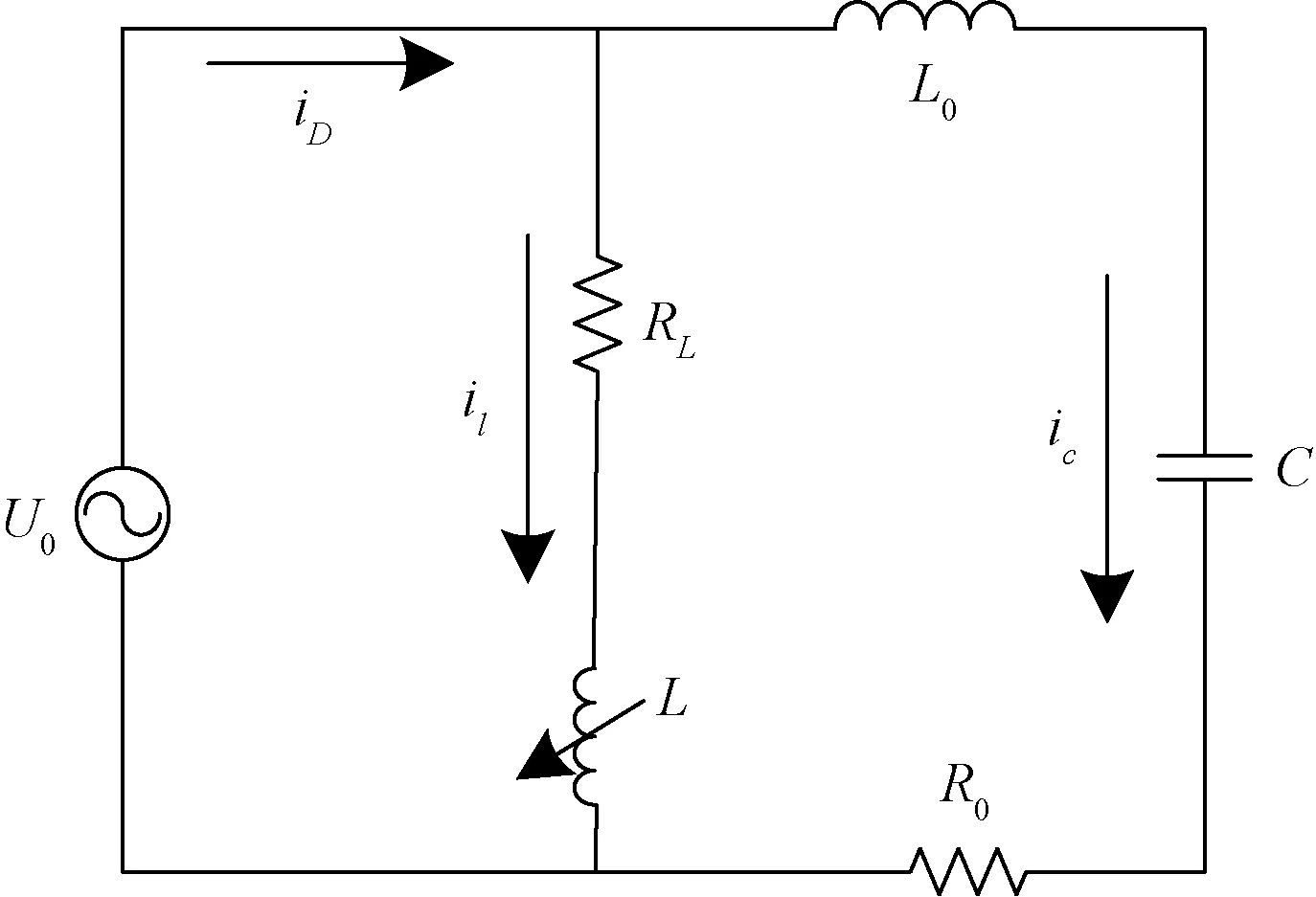
L0为等值电感；C为对地电容；RL为消弧线圈的电阻；R0为等值电阻；U0为电源电压；L为消弧线圈的电感；iD为故障零序电流；ic为电容电流；il为电感电流图1 单相接地暂态等值电路Fig.1 Single phase grounding transient equivalent circuit

iD=ic+il

=(Icm-Ilm)cos(ωt+φ)+

Ilmcosφe-t/τL

(1)

式(1)中：Ilm为最大电感电流；Icm为最大电容电流；ω为工频频率；φ为电压相位；ωf为震荡频率；τL为时间常数。

故障零序电流中稳态分量衰减速度快，振荡频率高；暂态分量衰减速度较慢，因此可以利用零序电流振荡频率与幅值的差异进行故障选线。采用CEEMD与LMD对各线路的零序电流进行分解，计算线路不同分量的能量熵值，利用SCN网络进行故障选线。

2 相关理论

2.1 互补集合经验模态分解

CEEMD算法是对EEMD算法的优化，通过给原始信号添加符号相反的白噪声，减少了本征模态分量(intrinsic mode function，IMF)重构时产生的误差，改善了模态混叠的问题[21],具体过程如下。

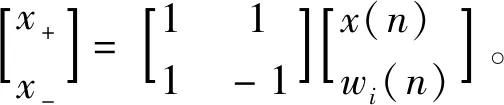
(3)CEEMD分解得到的IMF分量为

(2)

2.2 局部均值分解

LMD是一种非平稳信号的分解方法[22]，其算法在端点效应、虚假分量、过包络等问题上有所改善。对于信号x(t)的分解过程如下。

(1)找到x(t)的极值点ni，求解相邻极值点的均值mi与估计值ai，即

(3)

(4)

连接相邻mi与ai，用移动平均法得到局域均值函数m11(t)与包络估计函数a11(t)。

(2)将m11(t)从x(t)中分离出来，得到h11(t)，即

h11(t)=x(t)-m11(t)

(5)

(3)用h11(t)除以a11(t)，得到调频信号s11(t)，即

(6)

若a12(t)≠1，则需将s11(t)作为原数据重复(1)～(3)的迭代过程，直到s1n(t)的包络函数满足a1(n+1)(t)=1，即

(7)

(8)

(4)包络信号a1(t)为全部包络估计函数的乘积，即

a1(t)=a11(t)a12(t)…a1n(t)

(9)

(5)将a1(t)与s1n(t)相乘可得到PF分量，

即

PF1(t)=a1(t)s1n(t)

(10)

(6)在x(t)把PF1(t)分离出来能够得到信号u1(t)，将u1(t)视作初始信号x(t)重复(1)～(6)，当uN(t)为一个单调函数时停止循环。

最终x(t)分解为N个PF分量和uN(t)之和，即

(11)

2.3 随机配置网络

随机网络的特点是收敛速度快且泛化能力强[23]。文献[24]提出一种新型随机权神经网络，称为随机配置网络(stochastic configuration networks，SCN)。SCN是一个前向反馈网络，其标准模型如图2所示。

图2 标准SCN模型Fig.2 SCN standard model

第j个隐藏节点的输出为

(12)

则隐藏层输出矩阵hL(X)为

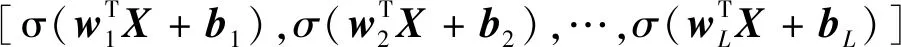
(13)

整个网络的输出为

Y=Hβ

(14)

式(14)中：β=[β1,β2,…,βM]L×M，H=[g1,g2,…,gL]N×L

SCN采用不等式进行约束，能够随机调整输入权重w和偏置b，利用最小二乘法来求解输出权重，这种赋值方法的优势在于能够降低模型训练时的计算复杂度缩短训练的时间。由于SCN的隐藏节点的数量是可以改变的，增加网络的节点数能够提高模型的逼近能力，这种独特的网络结构能够提高选线时分类的精确度。

3 基于CEEMD-LMD-SCN的集合型配电网故障选线步骤

故障选线流程如图3所示。配电网故障选线流程实现步骤如下。

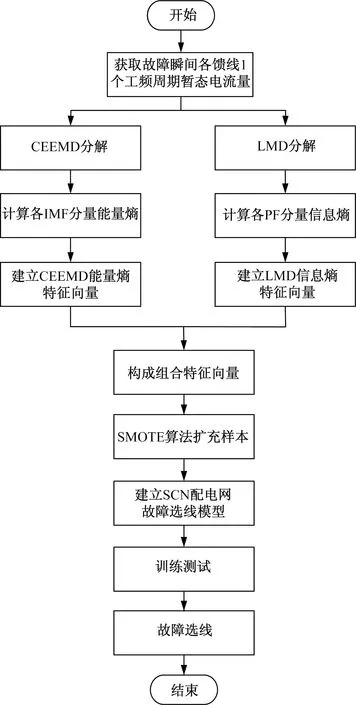
图3 配电网故障选线流程Fig.3 Fault line selection process of distribution network

(1)采集故障发生瞬间一个工频周期的时间窗数据。

(2)对故障瞬间各馈线的暂态零序电流信号进行CEEMD分解；对CEEMD分解所得IMF分量求取能量熵，利用CEEMD能量熵构造故障选线特征向量F=[Fa1Fa2…Fan，Fb1Fb2…Fbn，…，Fe1Fe2…Fen]1×5n。

(3)对故障瞬间各馈线的暂态零序电流信号xn(t)进行LMD分解；对LMD分解所得PF分量求取能量熵，利用LMD能量熵构造故障选线特征向量K=[Ka1Ka2…Kam，Kb1Kb2…Kbm，…，Ke1Ke2…Kem]1×5m。

(4)将CEEMD能量熵特征向量F=[Fa1Fa1…Fan，Fb1Fb2…Fbn，…，Fe1Fe2…Fen]1×5n和LMD能量熵特征向量K=[Ka1Ka2…Kam，Kb1Kb2…Kbm，…，Ke1Ke2…Kem]1×5m组合，形成能同时反映故障特征的组合特征向量θ=[Fa1Fa2…Fan，Fe1Fe2…Fen，Ka1Ka2…Kam，Ke1Ke2…Kem]1×5(n+m)。

(5)使用SMOTE算法扩充训练样本。

(6)将训练样本输入SCN中进行训练，得到基于CEEMD-LMD-SCN的集合型配电网故障选线模型。

(7)将测试集输入模型进行测试。

4 配电网故障仿真分析

4.1 配电网故障仿真模型

在PSCAD中搭建了110 kV/10.5 kV配电网模型，如图4所示。

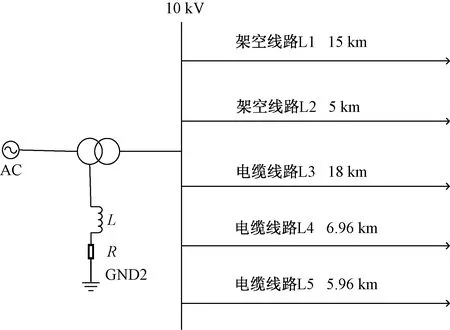
图4 配电网仿真模型Fig.4 Distribution network simulation model

设置架空线长度为15、5 km，电缆线长度为18、6.96、5.96 km。线路相关参数如表1所示。

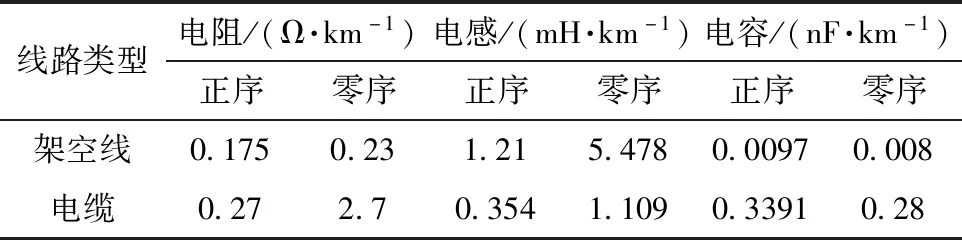
表1 线路正零序参数Table 1 Positive zero sequence parameters of line

若故障设置如表2所示，则各线路零序电流如图5所示。

表2 相关参数设置Table 2 Relevant parameter settings

图5 原始电流Fig.5 Original current

4.2 样本获取

4.2.1 CEEMD能量熵提取

当L1发生故障时，暂态电流分解后所得IMF分量如图6所示。

图6 CEEMD分解结果图Fig.6 CEEMD decomposition results

由图6可知通过对采集的暂态零序电流进行分解后有5个IMF分量，计算出各自的能量E1，E2，…，E5。将求得的能量值代入式(15)中求解每个IMF分量的能量熵，即

(15)

经计算求解出的CEEMD能量熵如表3所示。利用5条馈线的能量熵组成特征向量。

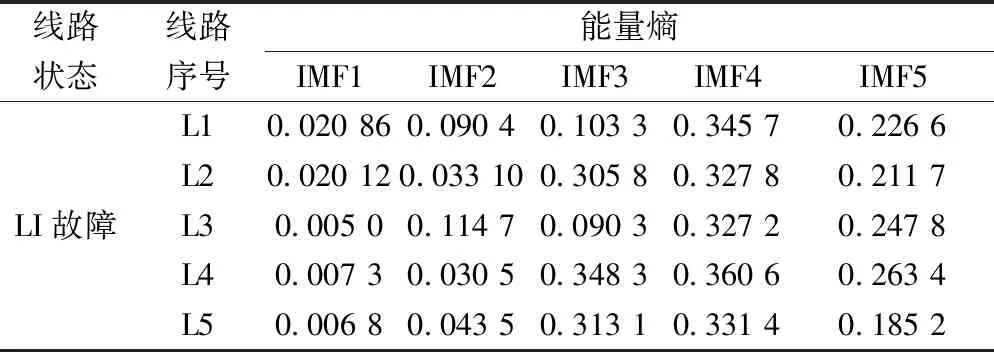
表3 CEEMD能量熵Table 3 CEEMD energy entropy

4.2.2 LMD能量熵提取

对L1线路故障状态下采集的暂态零序电流进行LMD分解，各线路分解后的所得的PF分量如图7所示。由图7可知通过对采集的暂态零序电流进行分解后有2个PF分量，计算出各自的能量E1、E2。将求得的能量值代入式(15)中求解每个PF分量的能量熵。如表4所示。利用5条馈线的能量熵组成特征向量。

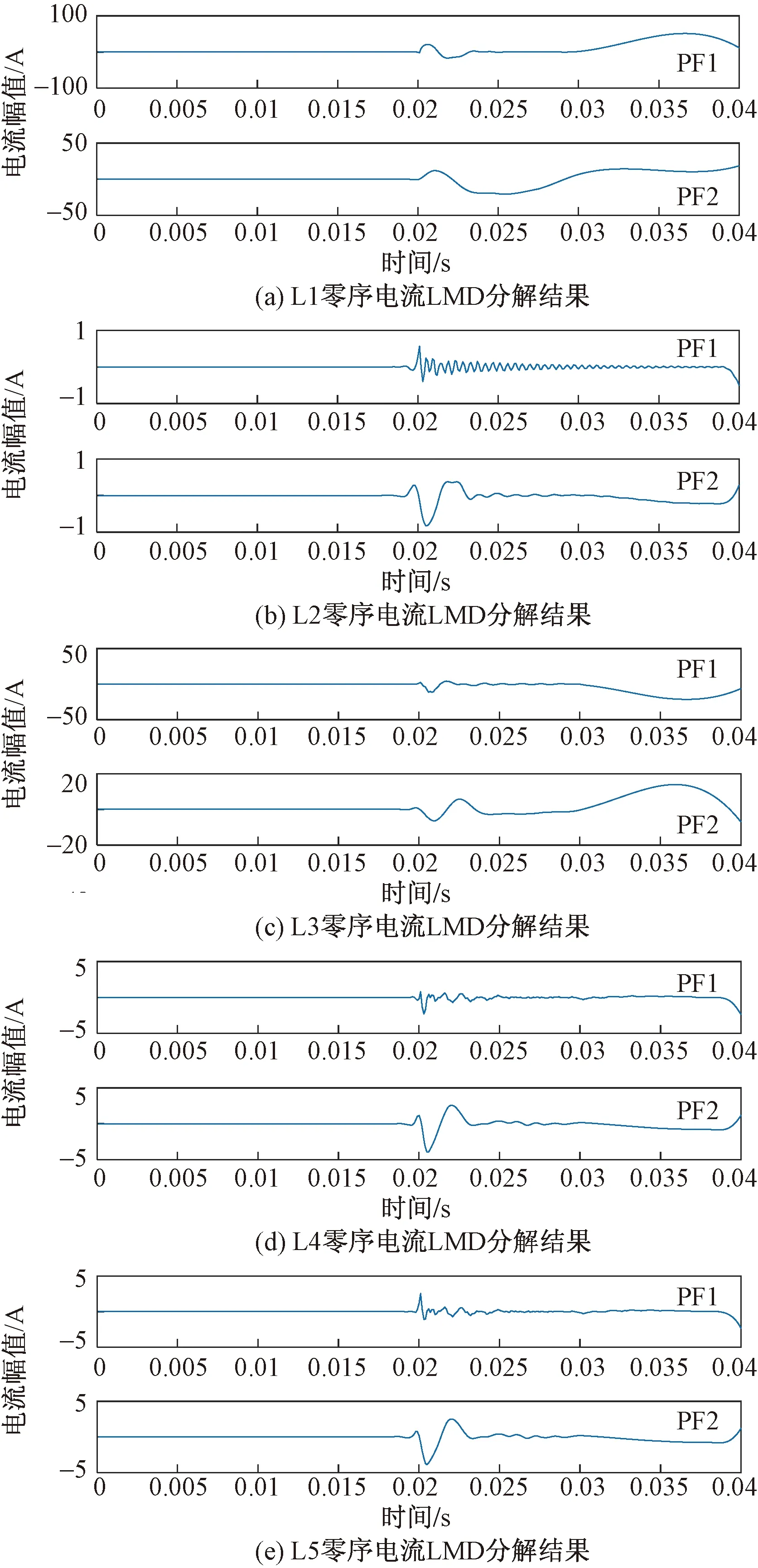
图7 LMD分解结果图Fig.7 LMD decomposition results

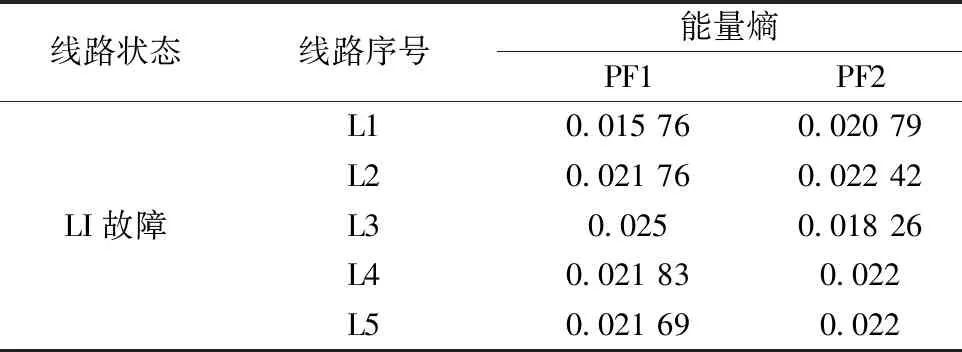
表4 LMD能量熵Table 4 LMD information entropy

4.2.3 组合特征向量的构建

为实现故障线路的判断，将CEEMD能量熵特征向量和LMD能量熵特征向量组合，形成能同时反映故障特征的组合特征向量。将组合特征向量作为SCN的输入向量，馈线编号L1～L5分别对应标签号1～5。

4.3 选线方法验证

4.3.1 建立基于SCN的智能故障选线模型

采样频率设置为10 kHz，采集故障发生瞬间一个工频周期的时间窗数据，考虑共5种不同位置的故障情况；考虑接地电阻为10、100、200、250、400、500共6种情况；初始角取0°、30°、45°、60°、90°、120°共6种角度，每条馈线的样本数为5×6×6=180组，考虑的故障线路包括2条架空线路和3条电缆线路共5条馈线，因此数据样本共5×180=900组。

4.3.2 样本扩充

由于训练SCN网络需要大量的数据样本，因此利用SMOTE算法扩充样本数据。SMOTE算法基本思路是采用随机线性插值的方式对样本进行扩充。

(16)

式(16)中：rand(0,1)为0～1间一个随机数。

用SMOTE算法将900组数据样本扩充至5 300组，将其作为训练样本。

4.3.3 训练样本识别结果分析

将5 300组训练样本输入SCN网络中进行训练，SCN网络设置迭代次数为300次，SCN训练过程中训练集的准确率与损失率变化曲线如图8所示。图8中可以看出，经过300次迭代后，准确率接近100%。从损失的变化曲线可以看出，损失率在逐渐下降，因此没有过拟合的问题。

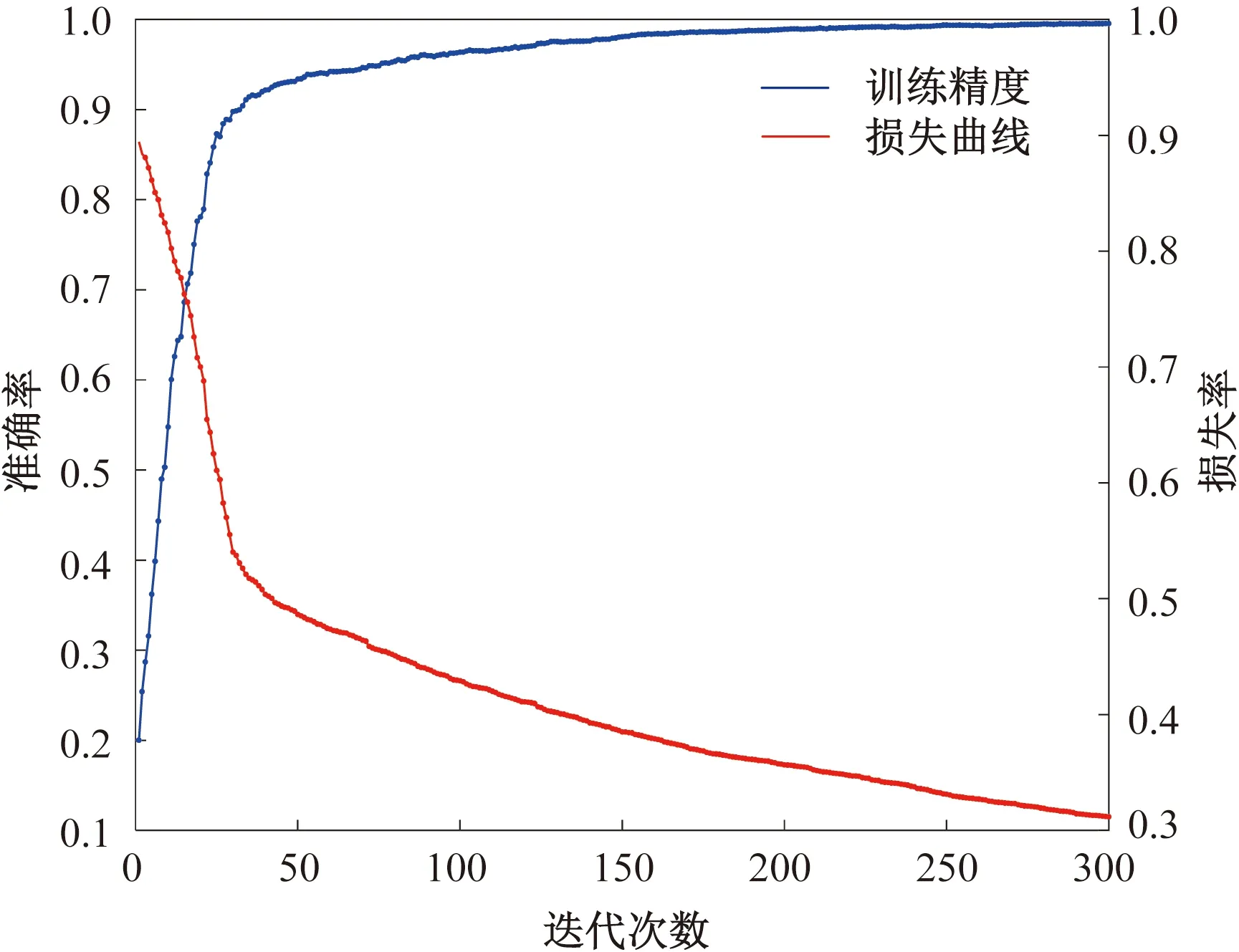
图8 训练过程中正确率和损失变化曲线Fig.8 Change curve of accuracy and loss during training

训练集的混淆矩阵如图9所示。将100组测试数据输入故障选线模型中，测试集的混淆矩阵如图10所示。从图10中的数据可以看出5条馈线分类结果的准确率均达到较高水平。L1、L3、L4、L5故障时均能被识别出来，仅有L5存在少量误判，体现了本文方法能够有效识别出故障线路。

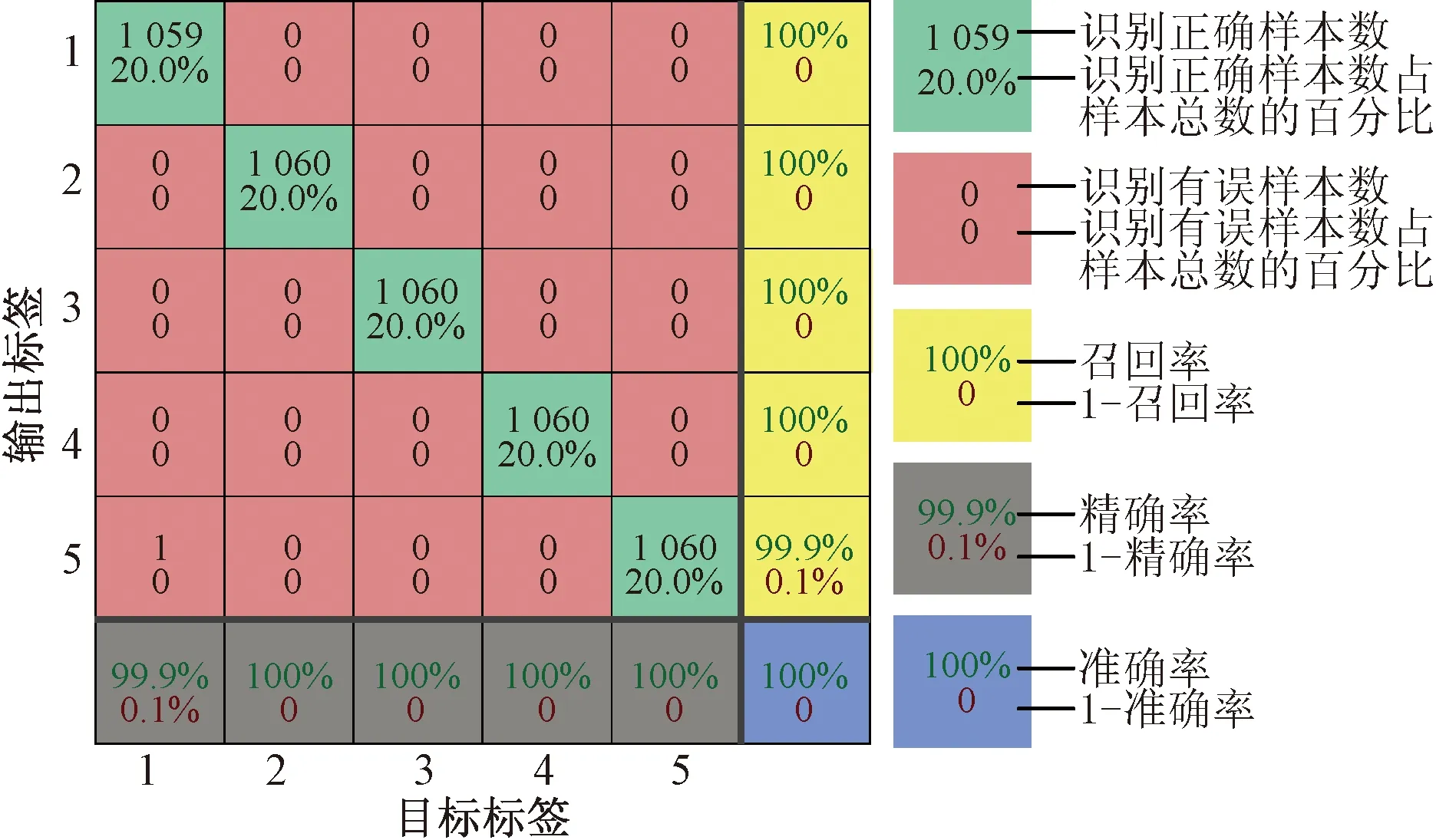
图9 训练集的混淆矩阵Fig.9 Confusion matrix of training set

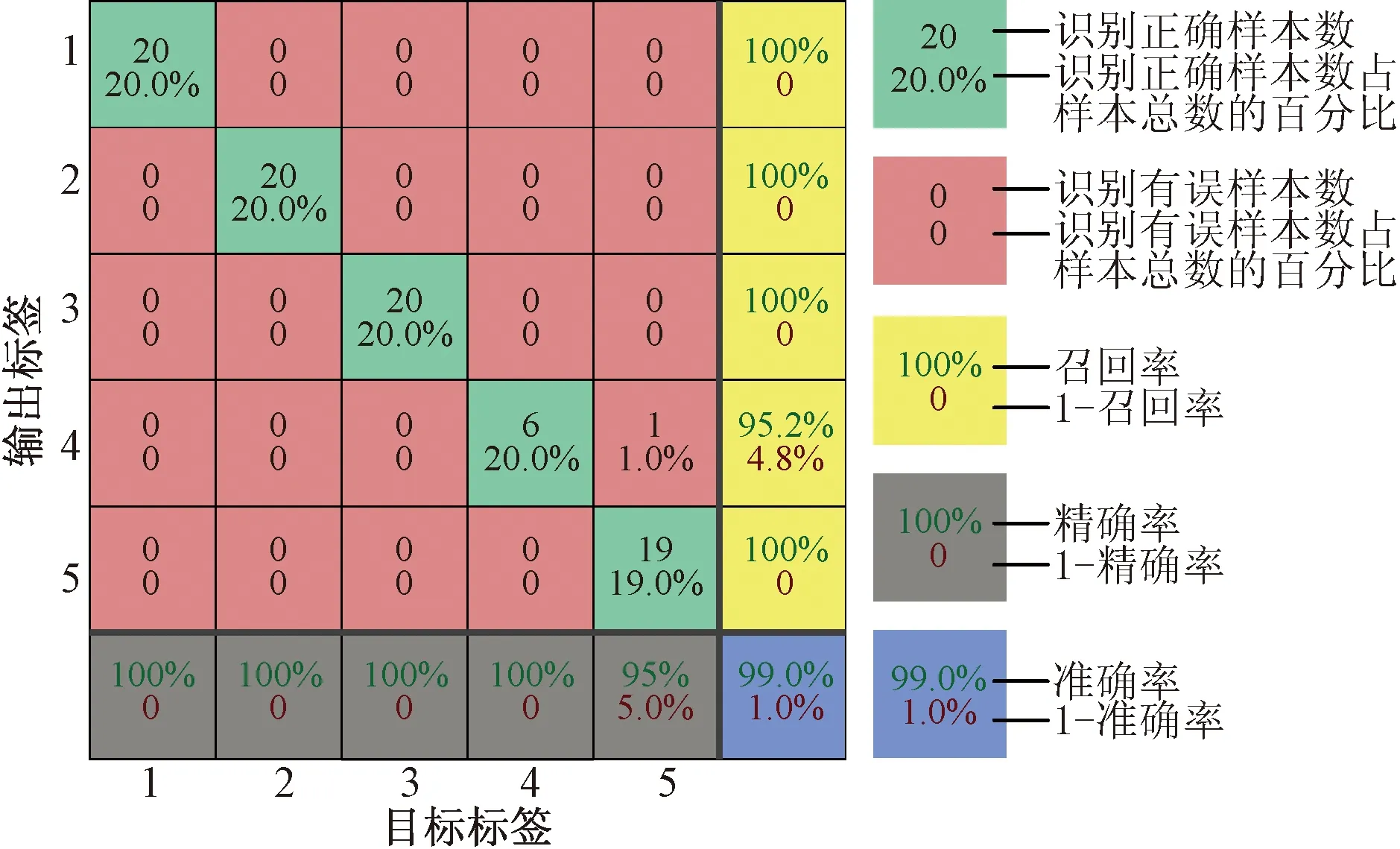
图10 测试集的混淆矩阵Fig.10 Confusion matrix of test set

5 适用性分析

5.1 改变接地电阻

为验证本文算法在接入不同接地电阻时的性能，提取接地电阻为150、300、450 Ω的故障特征输入SCN网络模型进行测试。混淆矩阵如图11所示，表5为仿真验证结果。

图11和表5表明，在不同接地电阻的情况下，该模型能够进行准确的故障识别和选线。

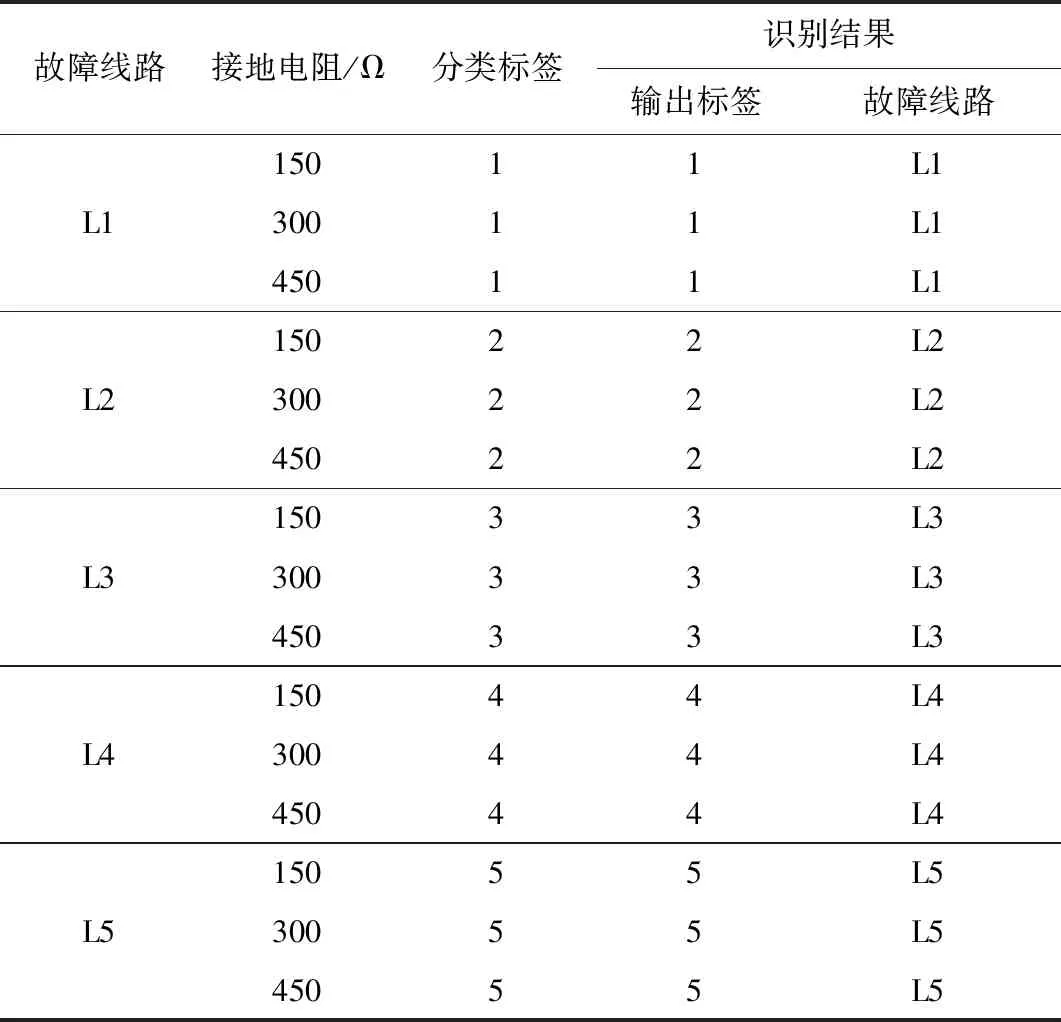
表5 不同接地电阻情况下的仿真验证结果Table 5 Simulation verification results under different grounding resistance

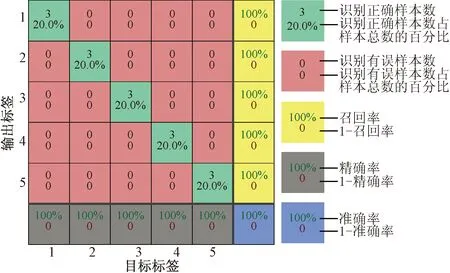
图11 不同接地电阻情况下的测试结果图Fig.11 Test results under different grounding resistance

5.2 改变故障位置

为验证线路在不同距离的情况下发生故障时本文算法的性能，提取出不同故障距离的故障特征进行测试。当L1距母线1、1.5、3 km发生故障时，提取其故障特征；当L2距母线1、5、10 km发生故障时，提取其故障特征；当L3距母线1、10 km发生故障时，提取其故障特征；当L4距母线3 km发生故障时，提取其故障特征；当L5距母线1、1.5 km发生故障时，提取其故障特征，并将所有故障特征输入SCN网络模型进行测试。混淆矩阵如图12所示，表6为仿真验证结果。

图12和表6表明，当线路在不同位置发生故障时，SCN网络能够有效识别出故障线路。

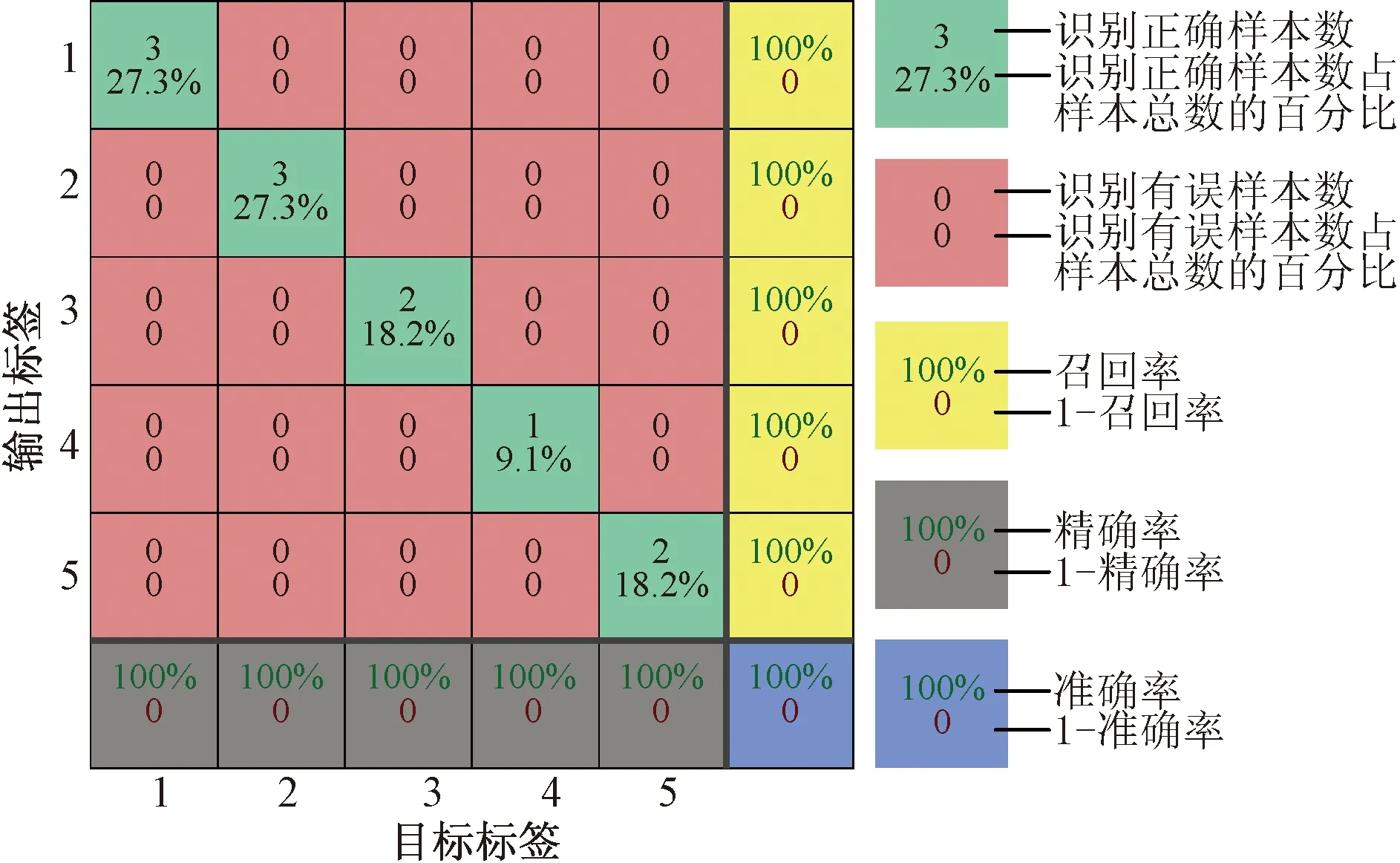
图12 不同故障距离情况下的测试结果混淆矩阵Fig.12 Confusion matrix of test results under different fault distances

5.3 改变故障初始角

为了验证在不同故障初始角度的情形下本文算法的性能,提取出不同故障初始角的故障特征进行测试。当L1发生故障时，提取故障初始角为0°、45°、90°的故障特征；当L2发生故障时，提取故障初始角为0°、45°、90°的故障特征；当L3发生故障时，提取故障初始角为0°、45°、90°的故障特征；当L4发生故障时，提取故障初始角为0°、30°、45°、60°、90°的故障特征；当L5发生故障时，提取故障初始角为0°、30°、45°、60°、90°的故障特征；并将所有故障特征输入至SCN网络中进行测试。混淆矩阵如图13所示，表7为仿真验证结果。

表6 不同故障距离情况下的仿真验证结果
Table 6 Simulation verification results under

different fault distances

故障线路故障距离距母线处/km分类标签识别结果输出标签故障线路L1111L11.511L1311L1L2122L2522L21022L2L3133L31033L3L4344L4L5155L51.555L5

从图13和表7可以看出该故障识别模型在不同故障初始角情况下能有效识别故障和故障选线。

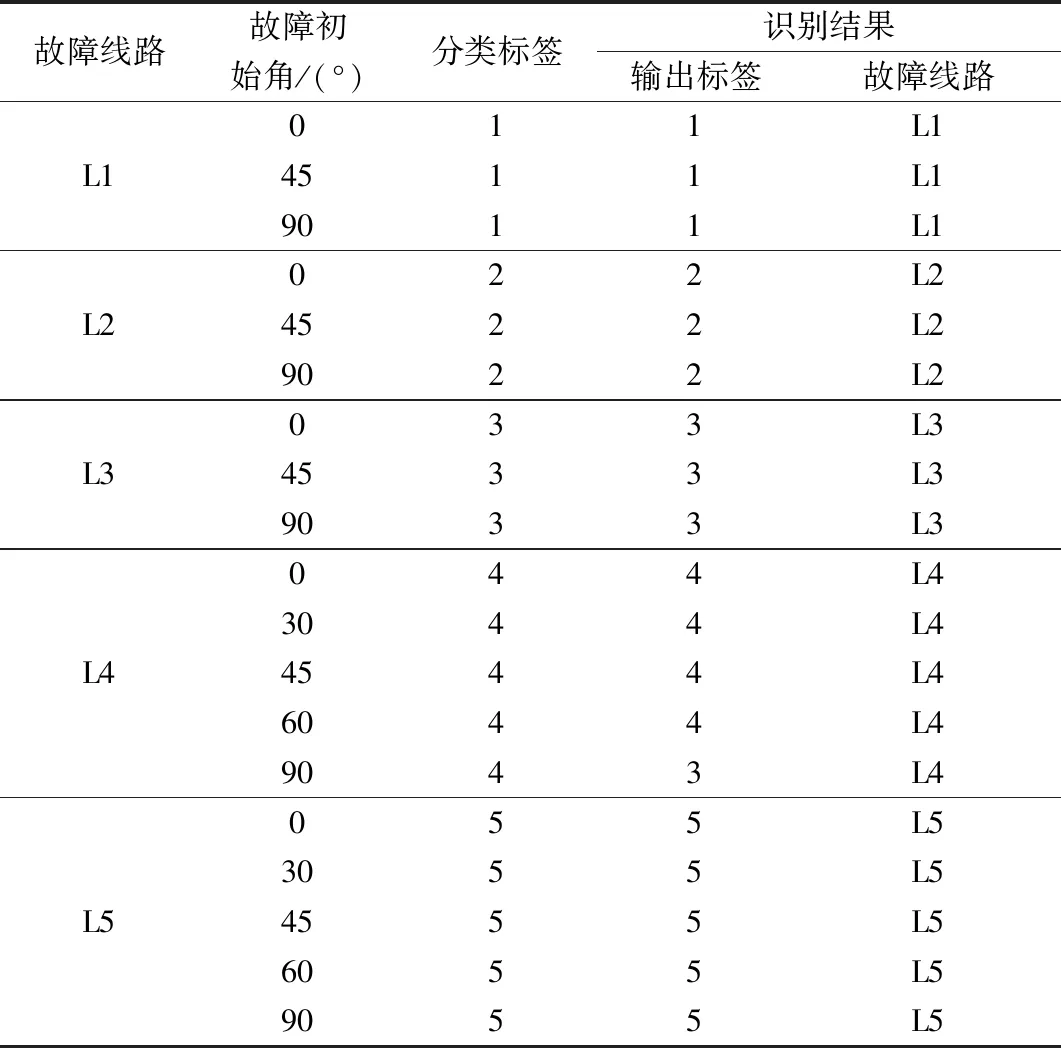
表7 不同故障初始角情况下的仿真验证结果Table 7 Simulation verification results under different fault initial angles

图13 不同故障初始角的测试结果混淆矩阵Fig.13 Test result confusion matrix of different fault initial angles

6 算法性能分析

6.1 与单一特征输入对比

为验证组合特征向量的优越性，采用相同参数的SCN模型对零序电流经CEEMD分解后的单一特征量进行训练和识别，分类结果如图14所示；采用相同参数的SCN模型对零序电流经LMD分解后的单一特征量进行训练和识别，如图15所示。

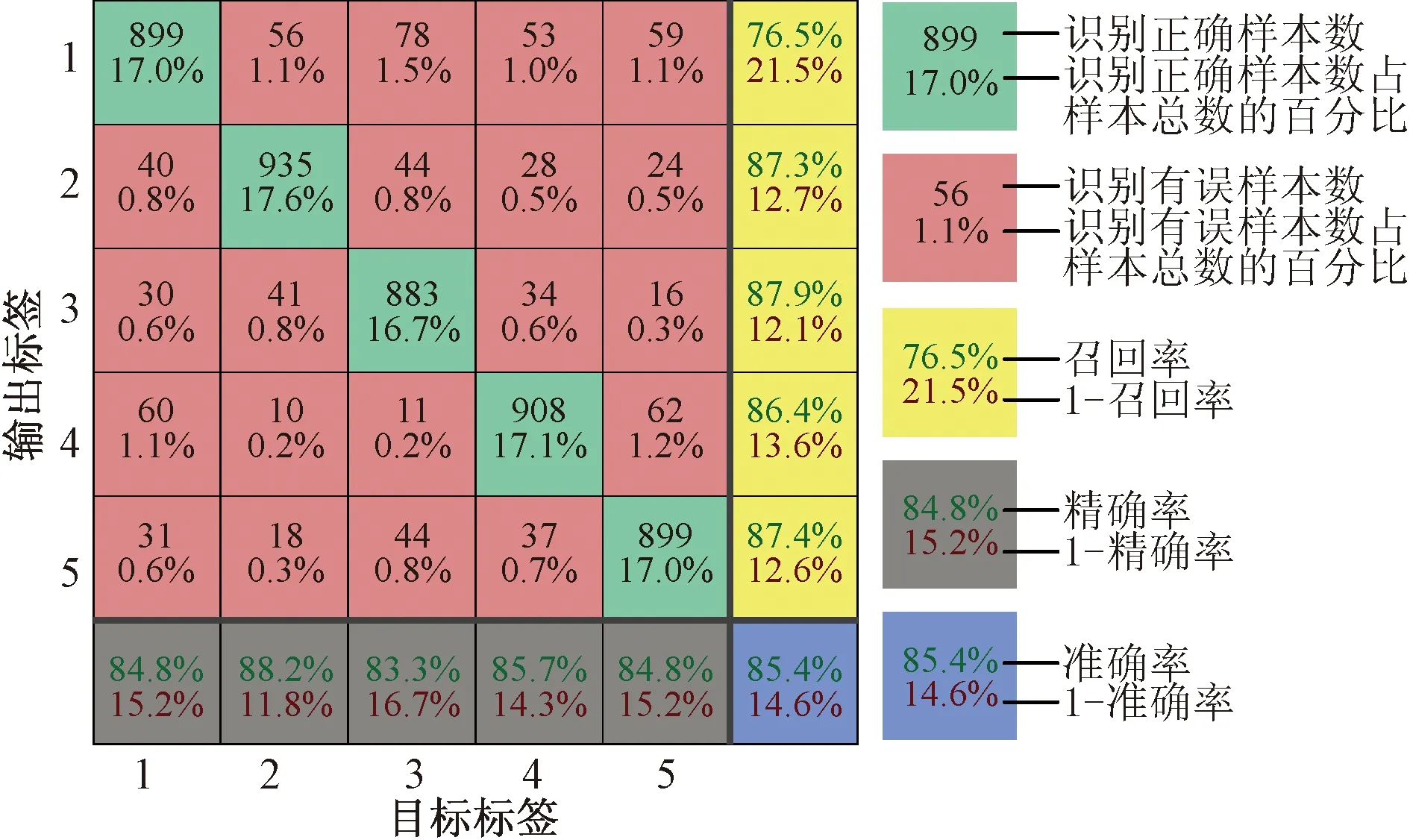
图14 经CEEMD分解后放入SCN分类得到的混淆矩阵Fig.14 After ceemd decomposition Put it into the confusion matrix obtained by SCN classification

图15 经LMD分解后放入SCN分类得到的混淆矩阵Fig.15 LMD decomposition and placeme Confusion matrix obtained by SCN classification

由图14可以看出经CEEMD分解后故障分类的准确率为85.4%，由图15可以看出经LMD分解后故障分类的准确率为94.6%。由此可知组合特征向量相比单一分解方法提取出的故障特征在故障选线中具有更好的识别效果。

6.2 抗噪声干扰

在实际工作中,由于电力设备上经常会出现大量噪声数据,因此为了验证本文算法在噪声影响状况下的可行性,在系统出现故障时采集的零序电流信号中,依次加入信噪比为50、60、70 dB的噪声模拟噪声影响的情况。图16为加入50 dB噪声波形图。

图16 50 dB噪声下L1零序电流Fig.16 L1 zero sequence current under 50 dB noise

将噪声测试样本输入SCN网络中进行测试，表8为噪声干扰情况下选线算法性能分析的结果。

从表8可以看出，当数据采集过程中存在噪声时，依然能对故障线路进行识别。

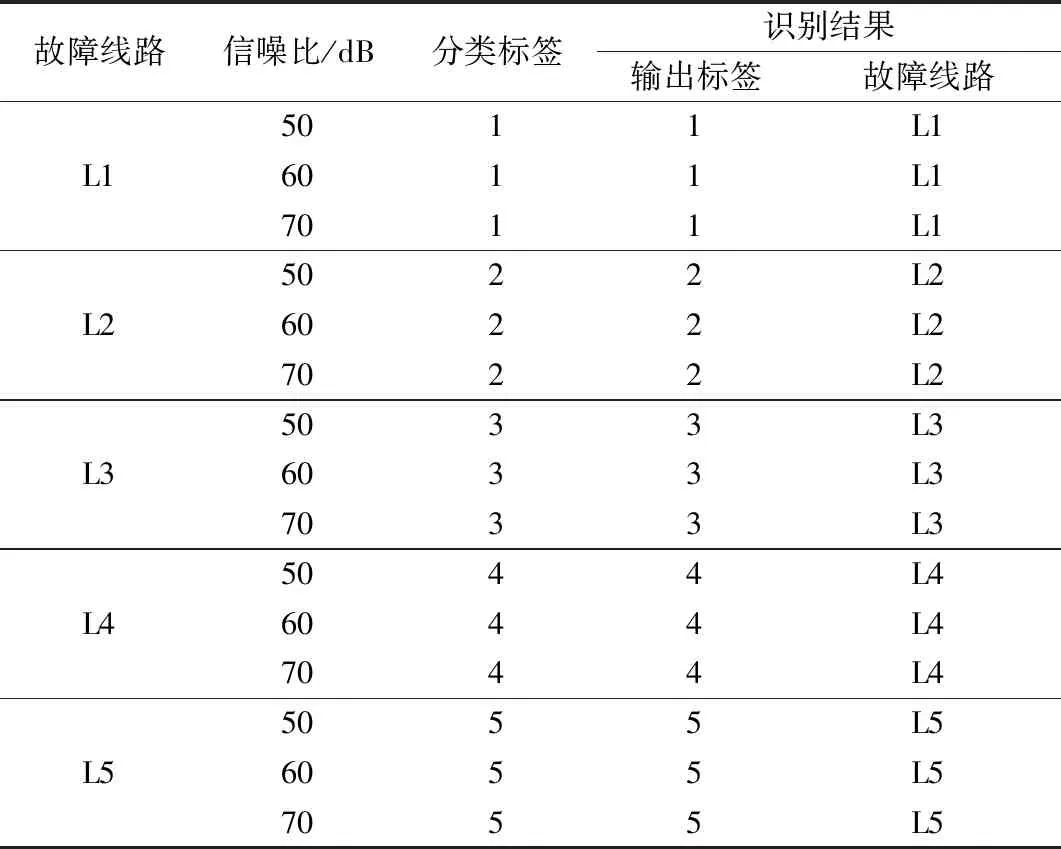
表8 噪声干扰情况下选线算法性能分析Table 8 Performance analysis of line selection algorithm under noise interference

6.3 高阻接地测试

由于暂态过程的故障特性并不明显,在高阻接地的情况下采用传统选线方法会产生误判,为了验证本文算法在高阻接地情况下的性能，接地电阻设置为2 000、2 500、3 000 Ω，提取高阻接地情况下的故障特征，并将所有故障特征输入到SCN中进行测试，混淆矩阵如图17所示，表9为仿真验证结果。

由图17与表9可以看出，当系统发生高阻接地时，该故障选线模型仍能准确的进行选线。

表9 高阻接地情况下选线算法性能分析Table 9 Performance analysis of line selection algorithm under high resistance grounding

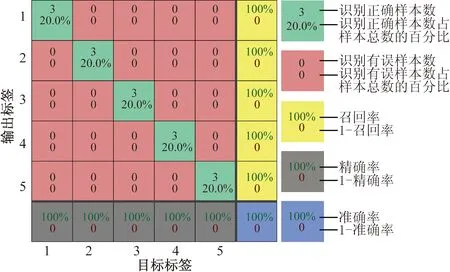
图17 高阻测试结果混淆矩阵Fig.17 Confusion matrix of high resistance test results

6.4 与其他网络对比

为验证SCN网络的优越性，将测试数据分别输入Softmax分类器、反向传播神经网络(back propagation，BP)、经引力搜索算法(gravitational search algorithm，GSA)优化的支持向量机(support vector machines，SVM)以及Elman中进行测试，各网络的分类结果如表10所示。

由表10可知，其他4种智能识别模型的识别率均没有SCN网络的识别率高。表明相比其他分类网络，SCN网络对组合特征的分类能力更加优越，具有更高的故障识别率。