基于核密度估计的构架应力谱外推与疲劳寿命分析

贺小洋 肖绯雄 杨 强 张远维 陈吉永

1西南交通大学牵引动力国家重点实验室 成都 610031 2中车大同电力机车有限公司 大同 037038

0 引言

应力谱是评估结构疲劳的基础，其充分性和完整性将直接影响评估结果的可靠性[1]。疲劳应力谱一般通过相关标准、有限元仿真和现场实测的方法获得，但当部件运营状况复杂时，通过标准和有限元仿真得到的应力谱难以反映零部件实际服役状况。因此，对结构进行现场动应力测试，根据测试载荷历程编制反映结构真实工作环境的应力谱，是轨道车辆领域普遍使用的疲劳寿命评估方法[2，3]。然而实际中的动应力测试经常受到时间、成本和实验场地等的限制，只能针对机械结构工作的典型工况进行短时间的应力时间历程测量。结构设计寿命一般长达数年到数十年不等，实测的数据往往仅占全寿命运营周期内的一部分，难以反映结构在较长时间内的抗疲劳服役性能，故需对结构短期内测试的动应力数据进行外推。

线性外推方法只是对载荷作用次数实现了拓展，难以体现结构受载的随机分布特性，雨流矩阵外推法是将应力时间历程转化为雨流矩阵实现外推的二维外推方法，分为参数外推和非参数法（核密度估计法）。由于均值频次和幅值频次一般具有明显的分布特点，早期的参数法通常采用威布尔分布拟合幅值频次，正态分布拟合均值频次[4]。然而，假设样本分布特征受主观影响较大，对于分布复杂且随机的样本会产生较大的拟合误差[5]。为避免对样本分布的假设，Dressler K等[6]首先将核密度估计运用到载荷谱的外推中，提出了基于雨流矩阵的核密度估计外推方法；宋清椿等[7]将该理论运用到农业机械构架应力谱编制中，得到了反映构架真实服役情况的载荷谱；牛文铁等[8]针对核密度估计计算量大的问题，提出了一种修正的核密度估计带宽计算方法；王秋实等[9]以实测动应力信号为对象，对核密度估计外推前后的应力谱的相关性等进行评价，得到了较为理想的外推结果。在上述研究中，对核密度估计方法进行了相关研究，但对于电力机车的相关研究还不够全面。

本文以某型电力机车构架拉杆座焊缝附近某点为研究对象，通过现场动应力测试和数据处理得到了测点幅值-均值雨流矩阵；研究了核密度估计方法中带宽的选取，并基于统计参数和灰色关联度对外推前后应力谱进行对比分析；根据外推后的长时载荷谱对构架焊缝进行疲劳寿命估计，以期能够为电力机车构架焊缝疲劳寿命预测提供思路。

1 应力测试与前处理

轨道车辆在运行过程中，轮对的磨损状况会使机车车辆的振动增大，导致相关零部件受力环境急剧变化[10]。在车辆整个运营过程中，单个镟轮周期内包含了车辆在服役过程中的受力演变状况，所以得到包含轮对不同状况下的应力谱，是进行外推和疲劳寿命评估的最好的选择[11]。

每个镟轮周期内车辆运行的里程均不相同，且实现全程动应力测试需要耗费大量时间以及巨大的成本，往往难以实现。本测试只针对镟轮前期和镟轮后期2个代表性工况进行动应力测试，一共测试2次。从车辆日常运营主要线路中，选取运营环境复杂的A站到B站，一个去程和回程作为完整测试区段。该段是具有典型的长大道、多曲线、多隧道和有短轨的山区线路。10 ‰～13 ‰连续坡道线路长度约为45 km，最大坡道为13 ‰，最小曲线半径为400 m，长度约为267.5 km。模拟实际列车正常运行状态，去程空车，回程拉货，运行速度为60～80 km/h，测试过程分为2段，在去程采集结束后重新采集回程。图1万采样测点的应变片位置图，应变片导线通过数据线接入机箱。

图1 应变片位置

最后将采集到的原始数据进行预处理，处理后的数据（包含去程和回程）如图2所示。通过图2的2组不同时期的动应力信号可知，镟轮前期构架拉杆座测点的最大动应力为22.27 MPa，最小动应力为-25.81 MPa；在轮对磨损程度较高的镟轮后期，该测点的最大和最小动应力达到了27.06 MPa和-32.88 MPa，同时中高应力幅值的循环频次也急剧增加，造成了远大于镟轮前期的疲劳损伤。

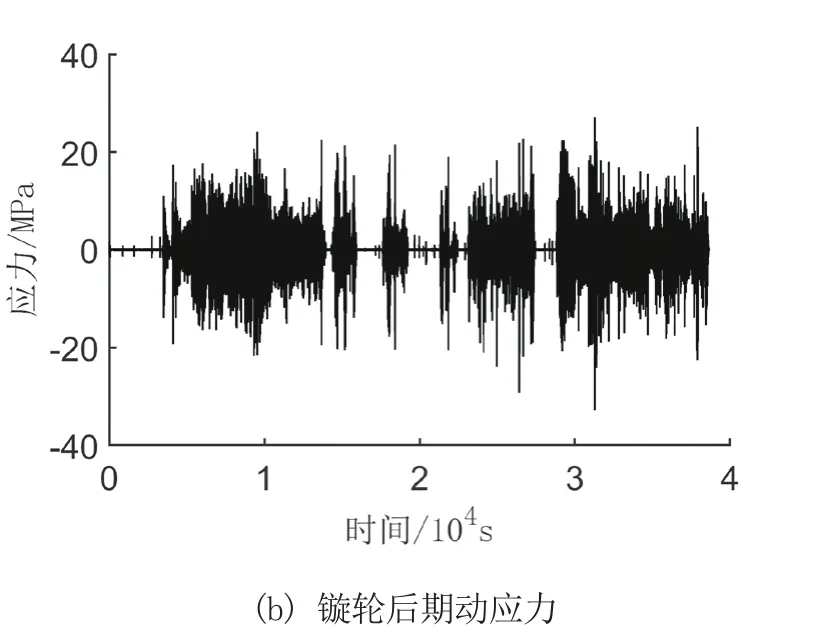
图2 动应力时域信号

2 核密度理论分析

核密度估计不需要事先对样本总体分布做出假设，只通过样本去估计总体的概率分布密度，是非参数密度估计法的一种。对于任意数据样本X=(x1，x2，…，xn)，假设其服从某个连续分布p（x），则其概率密度曲线可定义为

式中：n为样本数量；h为固定带宽，影响密度曲线光滑程度；k（*）为核函数，在全局上其值非负，积分的结果为1。

在核密度估计中，核函数相当于权函数，控制着估计点附近数据点的利用程度，其选取不会像带宽那样显著的影响估计结果[12]。常见的核函数有高斯核函数、Epanechikov核函数、余弦核函数、指数核函数和四次核函数等。其中高斯核函数的数学性质，可使得带宽的计算方法更为简便，本文选取常用使用的高斯核函数作为内核，即

2.1 带宽计算

带宽的选择关系着核密度估计的精度，从式（1）可以看出不同的带宽会导致不同的密度估计结果。不同带宽下的核密度结果反映了数据结构的不同特征，大带宽提供了未知密度下整体结构的图像，小带宽则揭示了未知密度下可能存在或不存在的局部结构[13]。因此，引入积分均方误差（MISE）来综合评估拟合概率密度分布与真实概率密度分布的误差，当最小积分均方误差最小时，h即为最优带宽。

式中：E(*)为数学期望，Bias(*)为样本偏差，var(*)为样本方差，o(*)为高阶残余项。

在带宽的计算中，一般可忽略其中的高阶残余项的影响。当积分均方误差最小，代表拟合误差最小。对式（3）求h的偏导数，令偏导数为0，可得最优带宽为

在式（4）中，核函数K(u)为已知项，密度函数p(x)为未知项，从而不能直接求解。一般情况下幅值近似服从正太分布，故计算带宽时可将p(x)看成正态分布求解。

在实际的幅值数据样本中，各个区域的稀疏程度存在较大差异。以镟轮前期样本为例，式（1）中的带宽是基于整个样本的固定带宽，难以兼顾密度差异较大的区间，如图3所示。固定带宽估计结果在低应力幅值处的概率密度偏低，导致中应力幅值处的概率密度增加。因此，引入具有自适应因子λi，由于每个xi都对应一个带宽。由图3可知，自适应带宽得到的概率密度曲线与幅值循环频次的分布特征较为吻合。

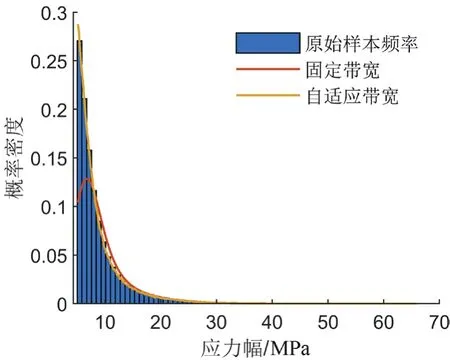
图3 不同带宽核密度估计结果比较

式中：α为灵敏因子，0≤α≤1，通常取0.5。

2.2 实测数据核密度估计

动应力测试得到的是载荷-时间历程信号，难以使用核密度方法进行样本外推。根据疲劳寿命评估理论，其对应的有效载荷幅值、均值和循环频次是计算零部件在该位置的疲劳寿命的基础[12]。雨流计数法将数据量巨大的动应力时域信号压缩成包含疲劳计算所需要的幅值-均值雨流矩阵，即减少计算量，又有利于进行载荷谱的外推。在对部件进行疲劳寿命评估时，通常认为幅值低于5 MPa的动应力循环载荷不造成损伤，可将其过滤掉[14]。镟轮初期与镟轮末期构架测点应力谱见图4。由于轮对磨损的原因，导致构架服役环境在不断变化，且镟轮后期的构架应力谱的幅值和频次远大于镟轮初期。如果只基于某单一样本进行外推将会得到过于保守或过于危险的疲劳寿命评估结果。将镟轮初期和末期的样本数据等权重组合，得到更能反应结构在一个镟轮周期下的服役状况的综合应力谱。经过处理过后的综合应力谱的幅值-均值雨流矩阵见图5。

图4 轮对不同时期应力谱

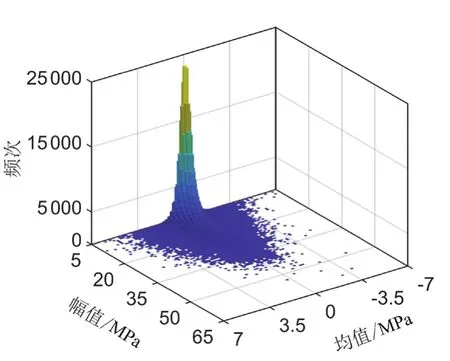
图5 应力幅值-均值雨流矩阵

应力均值不是影响疲劳寿命的主要因素，且由于整个运行过程中应力均值较小，对最终疲劳评估结果影响很小，故不考虑均值对疲劳寿命的影响。将处理后幅值样本作为核密度估计的数据输入，通过Matlab计算得到自适应带宽矩阵，然后再根据高斯核函数进行核密度估计，就得到如图6的样本概率密度曲线。从图6可以看出，通过核密度估计法所得的概率密度曲线呈现低应力幅值概率密度较大于高应力幅值的概率密度的特点，与频率直方图分布特性比较一致，并且采用自适应带宽算法所得到的概率密度曲线平滑程度也比较好。

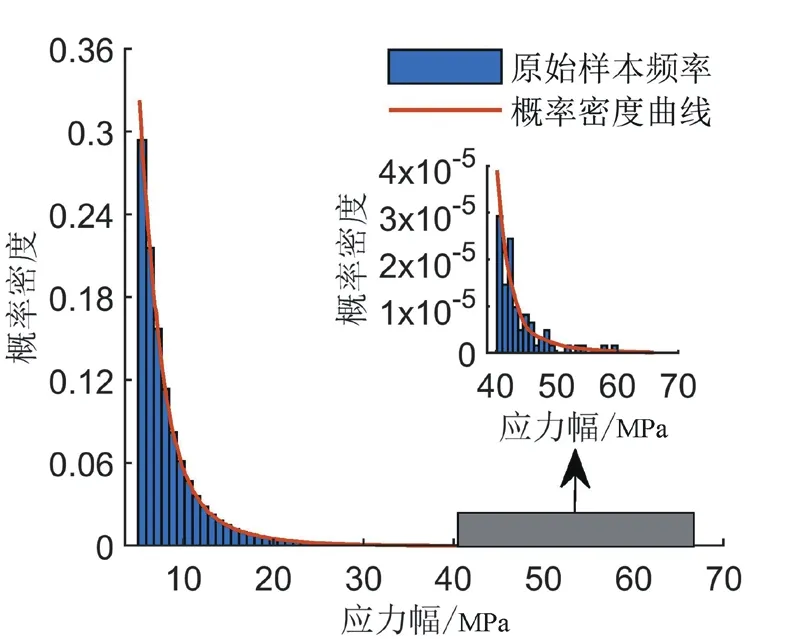
图6 样本频率与概率密度曲线

3 外推结果验证与疲劳寿命评估

3.1 统计参数评估

为了验证外推结果的有效性，根据图6的概率密度曲线使用蒙特卡洛模拟算法生成3组外推1倍的样本。当核密度外推方法选择合理时，外推前后的应力谱样本应该具有相同的特征。为了客观评价核密度估计的精度，提出从统计参数和灰色关联度等2个方面验证外推载荷的有效性。首先选取均值、标准差和最大值作为外推前后样本之间的评价依据，表1列出了各个外推样本与原始数据样本的统计参数。从表1可以看出均值、标准差和最大值与原数据样本的误差分别为2.8 %、1.3 %和9.4 %，均在小于10 %。表明外推载荷较好地保留了原始数据的统计特性。

3.2 灰色关联度检验

灰色关联度分析法可计算外推前后样本数据之间的关联度，两者关联度越高说明基于核密度估计得到的样本与原始样本有着较高的相似性[15]，具体过程为

1）对于任意n元素的对比序列，将原始序列g＝｛g1，g2，…，gn｝和进行对比的核密度外推序列g＇＝｛g＇1，g＇2，…，g＇n｝进行归一化处理。

2）通过2组数据的绝对差序列计算关联系数序列

3）计算关联度γ为

式中：m为绝对差序列的最小值；M为绝对差序列的最大值；φ为分辨系数，取0.5。

根据式（7）对外推前后应力谱的灰色关联度计算如表1。从表1可以看出3组外推样本与原始数据样本之间的灰色关联度均在0.9以上，说明两者之间的趋势一致性良好，外推数据保留了原始数据的分布特性。

表1 分析结果对比

3.3 疲劳寿命评估

为评估测点的安全可靠性，将外推系数设为10，对外推十倍后的长时应力谱进行疲劳寿命评估，并与线性外推后应力谱的疲劳寿命分析结果进行比较。对比分析如图7所示的10倍外推结果，可见线性外推方法只是对幅值进行了循环频次的扩展，而没有实现幅值的外推。核密度外推方法并完成了对幅值的拓展，其外推结果保留了原始数据的统计特征，反映了车辆运行状况的随机性。最后基于Miner线性损伤累积理论[16]，对测点进行疲劳寿命评估

图7 10倍外推后的应力谱

式中：D为应力谱作用下的累积疲劳损伤，K为外推应力谱的阶数，ni为第i阶应力幅的实际循环次数，Ni为第i阶应力幅在材料的S-N曲线上对应的循环次数。

该测试转向架构架为典型的焊接结构，可参照标准IIW—1823《焊接接头与部件的疲劳设计标准》进行疲劳寿命评估，通过式（6）计算即可得到累积损伤。基于线性外推10倍计算得到的疲劳损伤为0.011 8，而基于核密度估计外推10倍计算得到的疲劳损伤为0.012 2，对比分析可知，损伤增加了3.39 %，这是由于随着循环频次的扩展，核密度估计预测到了一些短期测试中未出现的较大的幅值载荷，使得基于核密度外推后的应力谱计算得到的疲劳损伤增加。

假设当测点损伤累积到1时发生疲劳破坏，则测点的疲劳寿命可由式（7）计算得到

对核密度外推和线性外推的疲劳寿命评估结果进行对比分析，基于线性外推10倍后计算的疲劳寿命结果为90.73万km，而基于核密度估计外推10倍后计算的疲劳寿命结果为87.94万km。可见基于线性外推得到的安全运营里程偏于危险，基于核密度估计得到的安全运营里程更偏于安全。

4 结语

1）本研究完成了现场车架动应力测试，获得了具有代表性的动应力时域信号，并基于核密度估计方法对样本进行了密度估计。结果表明，核密度估计方法具有很强的适应性，其估计的概率密度曲线与样本分布特征吻合度较高。

2）通过对外推前后应力谱进行统计参数对比分析和灰色关联度的计算，结果表明外推应力谱保留了测试应力谱的统计特征和分布特征，与基于线性外推计算疲劳寿命的方法相比，基于核密度估计外推的疲劳寿命评估方法预测到了其他可能出现的动应力幅值循环，对车辆安全运营里程的评估十分有益。